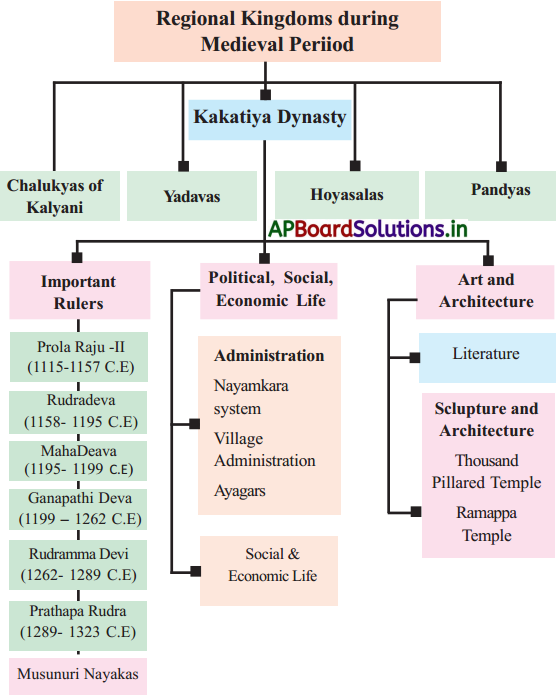
Students can go through AP Board 10th Class Maths Notes 6th Lesson శ్రేఢులు to understand and remember the concept easily.
AP Board 10th Class Maths Notes 6th Lesson శ్రేఢులు
→ కార్ల్ ఫ్రెడరిక్ గాస్ 1777 -1855
- కార్ల్ ఫ్రెడరిక్ గాస్ ప్రఖ్యాత జర్మన్ గణిత శాస్త్రవేత్త. ఇతను 30 – 4-1777 వ తేది జర్మనీలోని బర్వేలో ఒక పేద కుటుంబంలో జన్మించాడు.
- గాస్ తన చిన్నతనం నుండే గణితమువందు చాలా చురుకుగా ఉండేవాడు. గాస్ 10 సం॥ల వయస్సులోనే తన గణిత ఉపాధ్యాయుడు ఇచ్చిన సమస్య 1 నుండి 100 వరకు గల సహజ సంఖ్యల మొత్తం కనుగొనడంమ కొన్ని సెకనుల వ్యవధిలోనే పూర్తిచేసి ఉపాధ్యాయునికే సవాలు విసిరాడు. అతడు అనుసరించిన నియమాన్నే మనం అంకశ్రేణి n పదాల మొత్తం కనుగొనడంలో ఉపయోగిస్తున్నాము.
- ఇతమ గణితంలో అనేక సిద్ధాంతాలను ప్రవచించి నిరూపించాడు. ఆ సిద్ధాంతాలు అటు భౌతికశాస్త్రంలో కూడా ఉపయోగపడుతున్నాయి. గాస్ 77 సం||ల వయస్సులో ఫిబ్రవరి 23, 1855 న మరణించాడు.
→ చరిత్ర : 400 సం||లకు పూర్వమే – బాబిలోనియన్లకు అంకశ్రేణి, గుణ శ్రేఢులను గురించి తెలిసినట్లుగా ఆధారాలున్నాయి. బోథెన్సు (570 AD) ప్రకారము ఈ శ్రేఢులను గురించి పూర్వపు గ్రీకు రచయితలకు తెలిసినట్లుగా అర్థమౌతుంది. మొట్టమొదటిసారి ప్రముఖ భారతీయ ప్రాచీన గణితవేత్త ఆర్యభట్ట (క్రీ.శ. 470) మొదటిసారి మొదటి సహజ సంఖ్యల వర్గాల మొత్తము, ఘనాల మొత్తమునకు సూత్రాలను ఇచ్చినట్లుగా తన రచన ఆర్యభట్టీయం (క్రీ.శ. 499) నుంచి తెలుస్తుంది.
ఇంకా అంకశ్రేణిలో p వ పదం నుండి n వ పదం వరకూ గల పదాల మొత్తమును కనుగొనుటకు అవసరమైన సూత్రమును ఈయన ఇవ్వటం జరిగింది. బ్రహ్మగుప్తుడు (క్రీ.శ. 598), మహావీర (క్రీ.శ. 850) మరియు భాస్కర (క్రీ.శ. 1114 – 1185) వంటి ప్రాచీన భారతీయ గణితవేత్తలు మొదటి సహజ సంఖ్యల,వర్గాల మొత్తము మరియు ఘనాల మొత్తంలను గురించి చర్చించినట్లుగా తెలుస్తుంది.
![]()
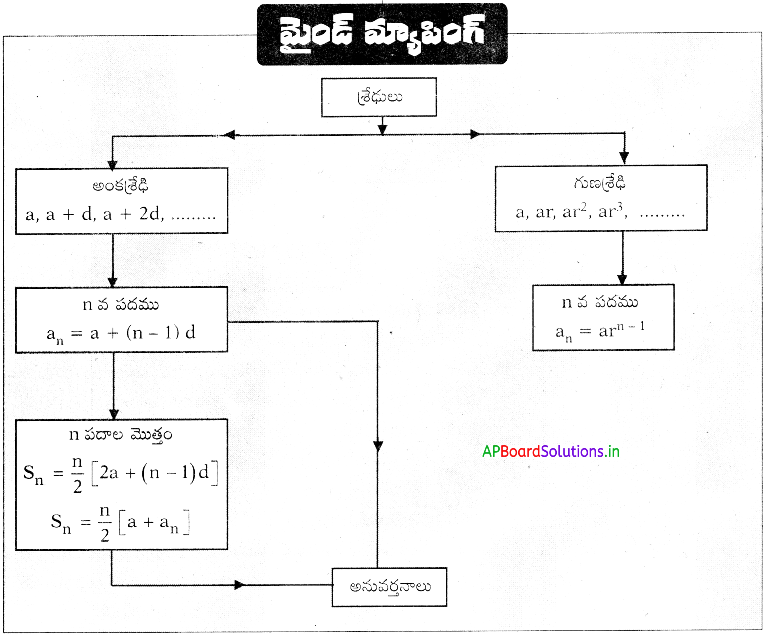
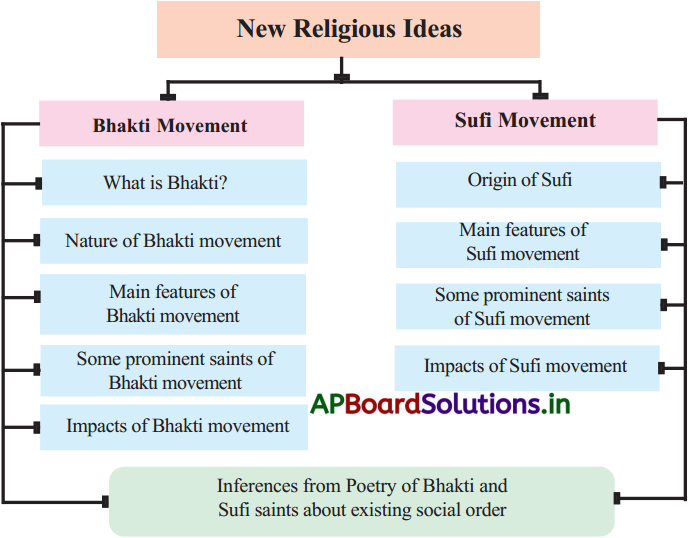
→ అంకశ్రేణి : ఒక సంఖ్యల జాబితాలో మొదటి పదం తప్ప మిగిలిన అన్ని పదాలు వాని ముందున్న పదానికి ఏదో ఒక స్థిరసంఖ్యను కలపటం వల్ల వస్తూ ఉంటే ఆ జాబితాను “అంకశ్రేణి” అంటాము.
కలిపే స్థిర సంఖ్యను “సామాన్య భేదము” లేదా “పదాంతరము” అంటాము. దీనిని ‘d’ తో సూచిస్తాము. ఇది. ధనాత్మకం లేదా ఋణాత్మకం లేదా సున్న కావచ్చును. మొదటి పదాన్ని ‘a’ తో సూచిస్తాము.
ఉదా : 5, 8, 11, 14, 17, 20, …………..
- పై సంఖ్యల జాబితాలో మొదటి పదం = 5.
- మొదటి పదానికి 3 కలిపిన రెండవపదం ‘8’ వస్తుంది.
- రెండవ పదానికి 3 కలిపిన మూడవపదం ’11’ వస్తుంది.
- మూడవపదానికి 3 కలిపిన నాలుగవపదం ’14’ వస్తుంది.
- ఇదే విధంగా మిగతా పదాలు వస్తున్నాయి. పై సంఖ్యల జాబితా అంకశ్రేణి అవుతుంది. కలిపే స్థిరసంఖ్య 3 సామాన్యభేదం (d), మొదటి పదం (a) 5 అవుతాయి.
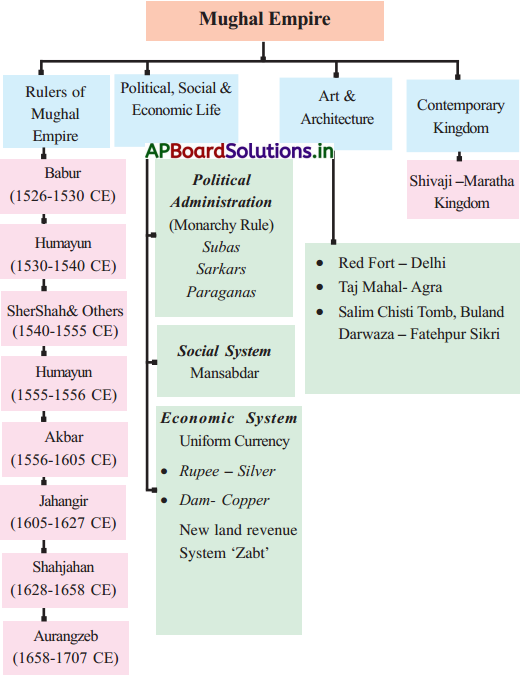
→ అంకశ్రేణిలోని మొదటి పదం a1
రెండవపదం a2
మూడవ పదం a3
………………….
………………….
n వ పదం an
మరియు సామాన్య భేదము d అనుకొంటే,
అంకశ్రేణి a1, a2, a3, ……… an మరియు
a2 – a1 = a3 – a2 = ……….. = an – an-1 = d (సామాన్య భేదం)
a2 = a1 + d
a3 = a2 + d = (a1 + d) + d = a1 + 2d
a4 = a3 + d = (a1 + 2d) + d = a1 + 3d
……………………..
……………………..
an = a1 + (n – 1) d అవుతాయి.
→ అంకశ్రేణి యొక్క సామాన్యరూపం : a, a + a, a + 2d, a + 3d, ……… a + (n – 1) d ను అంకశ్రేఢి యొక్క సామాన్యరూపం అంటాము.
గమనిక : ఒక సంఖ్యల జాబితాలో రెండు వరుస సంఖ్యల భేదం స్థిరమైన అది ఒక అంకశ్రేణి అవుతుంది.
a1, a2, a3, …………. ak, ak+1, ……… an అంకశ్రేఢి అయితే d = ak+1 -ak, k ≥ 1
→ అంకశ్రేణి యొక్క 1వ పదము (a) : a1, a2, a3, a4, ………. an, అయితే an ను అంకశ్రేణి యొక్క nవ పదం అంటారు. అంకశ్రేఢి యొక్క సామాన్య రూపం నుండి,
మొదటి పదం a1 = a = a + (1 – 1) d
రెండవపదం a2 = a + d = a + (2 – 1) d
మూడవపదం a3 = a + 2d = a + (3 – 1) d
నాలుగవపదం a4 = a + 3d = a + (4 – 1) d
………………………………
………………………………
n వ పదం an = a + (n – 1) d.
∴ అంకశ్రేణి యొక్క n వ పదం a = a + (n – 1) d
ఇక్కడ a మొదటి పదం, d సామాన్య భేదం
![]()
→ అంకశ్రేణిలోని n పదాల మొత్తం (S) : అంకశ్రేణిలోని n పదాలు a1, a2, a3, ………… , అయిన a1 + a2 + a3 + …………. + an, అంకశ్రేణిలోని n పదాల మొత్తం అవుతుంది. దీనిని Sn తో సూచిస్తాము.
Sn = a1 + a2 + a3 + a4 + ……. + an
S కు సూత్రాన్ని రాబట్టుకొందాం.

∴ 2Sn = n [2a + (n – 1) d] |
Sn = \(\frac{n}{2}\) [2a + (n – 1)d]
అంకశ్రేణిలో n పదాల మొత్తం Sn = \(\frac{n}{2}\) [2a + (n – 1)d]. ఒక అంకశ్రేణి యొక్క మొదటి పదం a, చివరి పదం an అయితే an = a + (n – 1) d మరియు
Sn = \(\frac{n}{2}\) [22 + (n – 1)d)
= \(\frac{n}{2}\)[a + a + (n – 1)d]
Sn = \(\frac{n}{2}\)[a + an]
Sn = \(\frac{n}{2}\) (మొదటి పదం + చివరి పదం)
గమనిక : అంకశ్రేణి యొక్క మొదటి పదం, సామాన్యభేదం, పదాల సంఖ్య తెలిసినపుడు n పదాల మొత్తాన్ని Sn = \(\frac{n}{2}\) [2a + (n – 1)d] సూత్రాన్ని, మొదటి పదం, చివరిపదం, పదాలసంఖ్య తెలిసి సామాన్యభేదం తెలియనప్పుడు Sn = \(\frac{n}{2}\)[a + an] సూత్రాన్ని ఉపయోగించి అంకశ్రేణి యొక్క n పదాల మొత్తాన్ని కనుగొంటాము. (చివరిపదం aను 1 గా కూడా సూచిస్తారు).
ఉదా : 5, 8, 11, 14, ……….. అంకశ్రేణిలో
15వ పదం :
మొదటి పదం a = 5
సామాన్యభేదం d = a, – a, = 8 – 5 = 3
nవ పదం an = a + (n – 1) d
15వ పదం a15 = 5 + (15 – 1) (3) = 5 + (14) (3) = 5 + 42 = 47
15వ పదం a15 = 47
15 పదాల మొత్తం : Sn = \(\frac{n}{2}\) [2a + (n – 1)d]
Sn = \(\frac{15}{2}\)[2(5) + (14)(3)] = \(\frac{15}{2}\) [10 + 42] = \(\frac{15}{2}\) × 52 = 390
15 పదాల మొత్తం S15= 390.
అలాగే పై ఉదాహరణలో మొదటి పదం 5, 15వ పదం 47 అయిన 15 పదాల మొత్తం
Sn = \(\frac{n}{2}\)[a + an)]
S15= 15 [5 + 47] = 15 (52) = 15 × 26 = 390
→ అంకశ్రేణిలోని (n – 1) పదాల మొత్తం Sn-1 మరియు n పదాల మొత్తం Sn అయిన ఆ శ్రేఢి nవ పదం an = Sn – Sn-1.
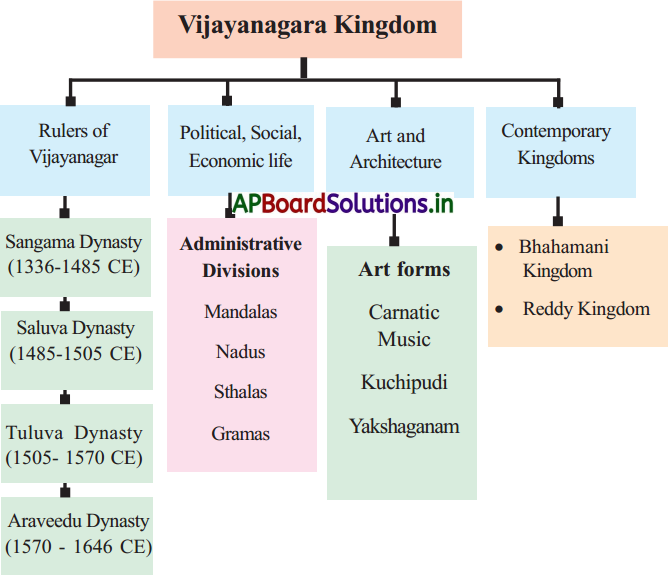
అనగా ఒక అంకశ్రేణిలో మొదటి n పదాల మొత్తం నుండి (n – 1) పదాల మొత్తాన్ని తీసివేసిన ఆ శ్రేణి యొక్క n వ పదము వస్తుంది.గుణశ్రేణి : ఒక సంఖ్యల జాబితాలో మొదటి పదం తప్ప మిగిలిన అన్ని పదాలు దాని ముందున్న పదాన్ని ఒక స్థిర సంఖ్యచే గుణించడం వస్తూ ఉంటే ఆ సంఖ్యల
జాబితాను గుణశ్రేణి అంటారు. ఈ స్థిర సంఖ్యను సామాన్య నిష్పత్తి ‘r’ అంటాము. గుణశేథి యొక్క మొదటి పదంను a చే, సామాన్యనిష్పత్తిని ‘Y’ చే సూచిస్తే ఆ గుణశ్రేణిలోని పదాలు
మొదటి పదం a1 = a
రెండవపదం a2 = ar
మూడవపదం a3 = ar – r = ar2
నాల్గవపదం a4 = ar . r = ar3
ఐదవపదం a5 = ar . r= ar4
………………………………..
………………………………..
nవ పదం, an = arn-1.
→ గుణశేథి యొక్క సామాన్య రూపం : a, ar, ar2, ar3, ………., arn-1
ఈ గుణశ్రేణిలో ఒక పదానికి, దాని ముందున్న పదానికి గల నిష్పత్తి r
∴ \(\frac{a r}{a}=\frac{a r^{2}}{a r}\) = ………. = r.
a1, a2, a3, ……… an ఒక గుణ శ్రేణి కావలెనన్న ప్రతిపదము శూన్యేతరము అవుతూ \(\frac{a_{n}}{a_{n-1}}\) = r కావలెను.
ఇక్కడ n ∈ N మరియు n > 1.
గుణశ్రేణిలో 1వ పదము : a1, a2, a3, ……… an గుణశ్రేణి అయితే an ను ఆ గుణశ్రేణి యొక్క nవపదం అంటారు. మొదటి పదం a-గాగల a1, a2, a3, ……… an గుణశ్రేఢి యొక్క సామాన్య నిష్పత్తి / అయితే
a1 = a = ar1-1
a2 = a . r = ar = ar2-1,
a3 = ar r = ar2 = ar3-1
a4 = ar . r = ar3 = ar4-1
…………………………………………
…………………………………………
…………………………………………
an = arn-1
an = arn-1 గుణశ్రేణి యొక్క nవ పదం అవుతుంది.
గుణశ్రేఢి యొక్క 1వ పదం an = a . rn-1.