Srinivas

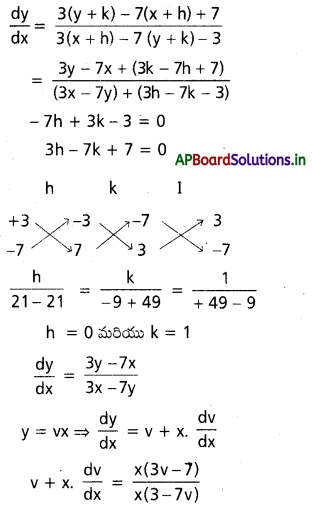
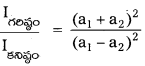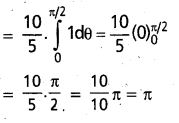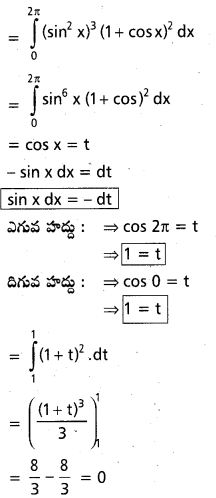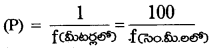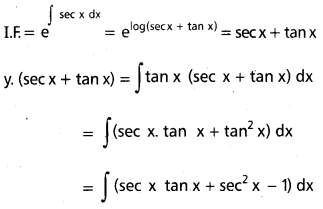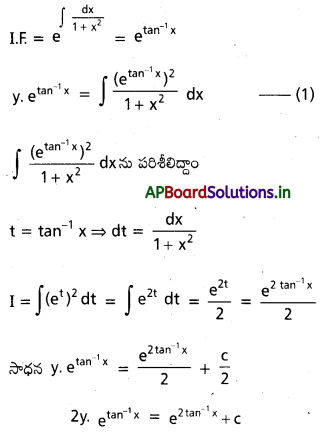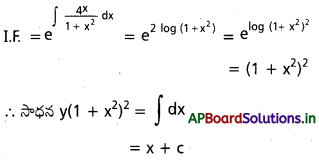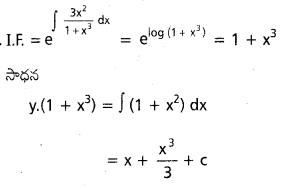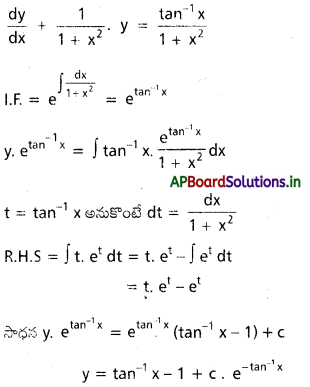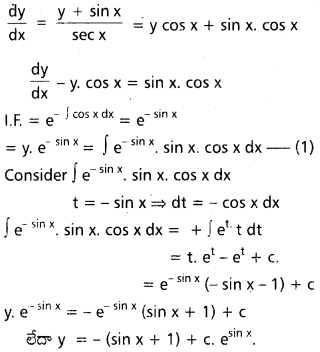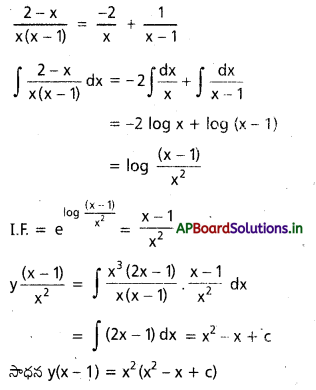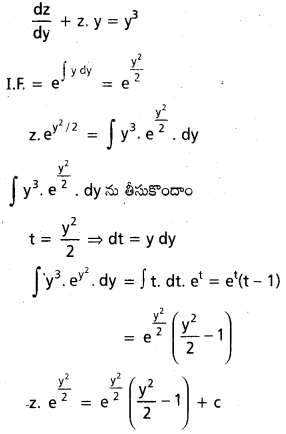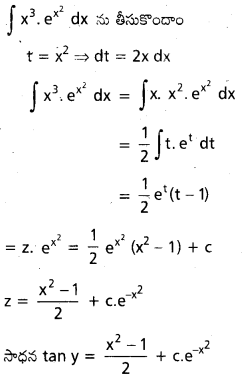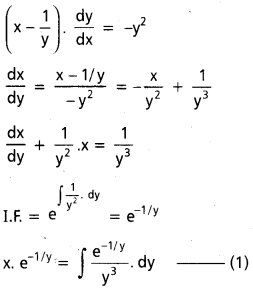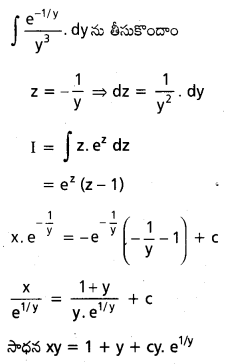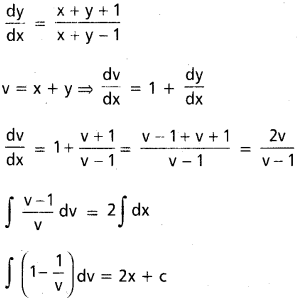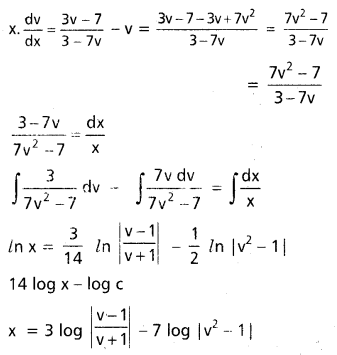Students can go through AP Inter 2nd Year Physics Notes 4th Lesson విద్యుత్ ఆవేశాలు, క్షేత్రాలు will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 4th Lesson విద్యుత్ ఆవేశాలు, క్షేత్రాలు

→ ఆవేశ వస్తువుల పరిమాణం, వాటి మధ్య దూరంతో పోల్చిన చాలా తక్కువగా ఉంటే, వాటిని బిందు ఆవేశాలు అంటారు.

→ వస్తువు యొక్క మొత్తం ఆవేశం, ఎల్లప్పుడు ప్రాథమిక ఆవేశంనకు పూర్ణాంక గుణిజాలుగా ఉంటే విద్యుత్ శక్తి నిత్యత్వమయింది అంటారు. i. e., Q : = ne ఇక్కడ n = 0, +1, +2, ±3.

→ రెండు స్థిర ఆవేశాలు కొంత దూరంలో ఉన్నప్పుడు వాని మధ్య పనిచేసే బలంను కులూమ్ నియమము ఇస్తుంది. స్థిర విద్యుత్ బలం, రెండు ఆవేశాల దూరం యొక్క వర్గంనకు విలోమానుపాతంలో ఉండుట వల్ల, దీనిని విలోమ వర్గనియమము అని కూడా అంటారు. యానకంలో కూలుమ్ నియమము
F = \(\frac{1}{4 \pi \varepsilon} \cdot \frac{q_1 q_2}{r^2}\) ఇక్కడ & యానకం పెర్మిటివిటీ.

→ యానకం రోధక స్థిరాంకం, K = \(\frac{\varepsilon}{\varepsilon_0}\)

→ రెండు ఆవేశాల మధ్య స్థిర విద్యుత్ బలం, మిగిలిన ఆవేశాల వల్ల ప్రభావం కాదు అనే ప్రాథమిక సూత్రంపై అధ్యారోపణ సూత్రం ఆధారపడింది.

→ ఏదైనా బిందువు ప్రమాణ ఆవేశంను ఉంచితే దానిపై పనిచేయు బలంను విద్యుత్ క్షేత్ర తీవ్రత అంటారు.

→ బలరేఖ వక్రంపై ఏదైనా బిందువు వద్ద గీసిన స్పర్శరేఖ, ఆ బిందువు వద్ద విద్యుత్ క్షేత్రం దిశను తెలుపును. విద్యుత్ బలరేఖలు సంవృత వక్రాలు కావు.

→ విద్యుత్ అభివాహం, Φ_E = ∮_sE.dS మూలకం వైశాల్యం dS ఒక సదిశ మరియు దిశ వైశాల్యంనకు లంబంగా వెలుపలకు ఉండును. విద్యుత్ అభివాహం ఒక అదిశ.

→ సంవృత తలం ద్వారా మొత్తం అభివాహం, తలం లోపల ఉన్న మొత్తం ఆవేశంనకు \(\frac{1}{\varepsilon_0}\) రెట్లు ఉండునని కూలుమ్ నియమము నిర్వచిస్తుంది.
Φ_E = ∮_sE.dS = \(\frac{\mathrm{q}}{\varepsilon_0}\)

→ ప్రమాణ ధనావేశంను అనంత దూరం నుండి స్థిర విద్యుత్ బలంనకు వ్యతిరేకంగా క్షేత్రంలోని ఒక బిందువు వద్దకు తీసుకురావటానికి జరిగిన పనిని, ఆ బిందువు వద్ద విద్యుత్ పొటెన్షియల్ అంటారు.

→ స్వేచ్ఛాతలంలో బిందు ఆవేశం q వల్ల r దూరంలో విద్యుత్ క్షేత్ర తీవ్రత E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{\mathrm{q}}{\mathrm{r}^2}\)

→ స్వేచ్ఛాతలంలో బిందు ఆవేశం q వల్ల r దూరంలో విద్యుత్ పొటెన్షియల్ V = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r}\)

→ సమాన, వ్యతిరేక ఆవేశాలు జంట q మరియు – q లు 2a దూరంలో వేరుచేయబడి ఉంటే, దానిని విద్యుత్ ద్విధ్రువము అంటారు.

→ అధ్రువ అణువులలో ధనావేశ కేంద్రము మరియు రుణావేశ కేంద్రము ఏకీభవించును.
ఉదా : CO₂, CH₄. వీటికి ద్విధ్రువ భ్రామకం సున్నా.

→ ధ్రువ అణువులలో ధనావేశ కేంద్రము మరియు ఋణావేశ కేంద్రములు ఏకీభవించవు.
ఉదా : H₂O. వీటికి శాశ్వత ద్విధ్రువ భ్రామకం ఉండును.

→ వస్తువు యొక్క ప్రమాణ ఉపరితల వైశాల్యంపై ఆవేశంను, ఆవేశ తల సాంద్రత అంటారు. σ = \(\frac{\Delta Q}{\Delta S}\)

→ తీగ ప్రమాణ పొడవుపై గల ఆవేశంను, రేఖీయ ఆవేశ సాంద్రత అంటారు. λ = \(\frac{\Delta \mathrm{Q}}{\Delta l}\)

→ వస్తువు ప్రమాణ ఘనపరిమాణంలో ఉండే ఆవేశంను, ఘనపరిమాణ ఆవేశ సాంద్రత అంటారు. p = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{V}}\)

→ అనంత పొడవు, ఏకరీతి ఆవేశిత తీగవల్ల క్షేత్రం, E = \(\frac{\lambda}{2 \pi \varepsilon_0 \mathrm{r}}\)

→ ఏకరీతి ఆవేశం ఉన్న అనంత సమతల పలక వల్ల క్షేత్రం, E = \(\frac{\sigma}{2 \varepsilon_0}\)

→ పలుచని గోళాకార కర్పరము, ఏకరీతి ఆవేశతల సాంద్రత 6 అయితే

• E = \(\frac{\mathrm{q}}{4 \pi \varepsilon_0 \mathrm{r}^2}\)(≥ R)
• E = 0 (r < R). → విద్యుత్ ద్విధ్రువం మధ్య బిందువు నుండి మధ్యగత రేఖపై r దూరంలో క్షేత్రం, E = \(\frac{\mathrm{P}}{4 \pi \varepsilon_0} \frac{1}{\left(\mathrm{a}^2+\mathrm{r}^2\right)^{3 / 2}}\) r >> a. అయితే
  E = \(\frac{-\mathrm{P}}{4 \pi \varepsilon_0 \mathrm{r}^3}\)

→ ద్విధ్రువం అక్షంపై కేంద్రము నుండి 1 దూరంలో విద్యుత్ క్షేత్ర తీవ్రత, E = \(\frac{2 {Pr}}{4 \pi \varepsilon_0\left(\mathrm{r}^2-\mathrm{a}^2\right)^2}\) r >> a అయితే E = \(\frac{2 \mathrm{P}}{4 \pi \varepsilon_0 \mathrm{r}^3}\)

→ ఏకరీతి విద్యుత్ క్షేత్రం E లో, ద్విధ్రువం ప్రయోగించు టార్క్ τ = P × E.
ఫార్ములాలు

→ కూలుమ్ నియమము \(\overrightarrow{\mathrm{F}}=\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2} \hat{\mathrm{r}}\) లేక \(\overrightarrow{\mathrm{F}}=\frac{1}{4 \pi \varepsilon_0} \times \frac{\mathrm{q}_1 \mathrm{q}_2}{|\overrightarrow{\mathrm{r}}|^3} \times \mathrm{r}^3\)

→ అధ్యారోపణ సూత్రం, \(\overrightarrow{\mathrm{E}}=\frac{\mathrm{q}}{4 \pi \varepsilon_0} \sum \frac{\mathrm{q}_{\mathrm{i}}}{\mathrm{r}_1^2} \widehat{\mathrm{r}}_{\mathrm{i}}\)

→ రోధక స్థిరాంకం లేక సాపేక్ష పెర్మిటివిటి K లేక ε_r

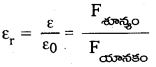
→ సదిశ రూపంలో కూలుమ్ నియమము,

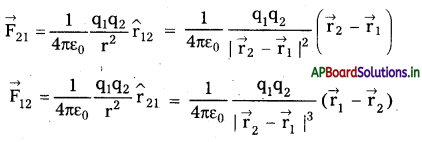
→ ఏకరీతి ఆవేశ అంగుళీయకము (రింగు) అక్షంపై ఏదైనా బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q \mathrm{x}}{\left(\mathrm{x}^2+\mathrm{a}^2\right)^{3 / 2}}\)
x >> a, అయితే, అప్పుడు E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{x^2}\)

→ విద్యుత్ ద్విధ్రువ భ్రామకం \(\overrightarrow{\mathrm{P}}_{\mathrm{e}}=\mathrm{q}(2 \overrightarrow{\mathrm{a}})\)

• అక్షీయ రేఖపై విద్యుత్ క్షేత్ర తీవ్రత \(\overrightarrow{\mathrm{E}}_{\mathrm{a}}=\frac{2 \overrightarrow{\mathrm{p}} \cdot \mathrm{r}}{4 \pi \varepsilon_0\left(\mathrm{r}^2-\mathrm{a}^2\right)^2}\)
• మధ్య లంబ తలంపై ఏదైనా బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత \(\overrightarrow{\mathrm{E}}_{\mathrm{eq}}=\frac{\overrightarrow{\mathrm{P}}}{4 \pi \varepsilon_0\left(\mathrm{r}^2-\mathrm{a}^2\right)^{3 / 2}}\)

→ ఏకరీతి విద్యుత్ క్షేత్రంలో ఉన్న విద్యుత్ ధ్రువంపై పనిచేయు టార్క్ τ = PEsin θ
సదిశ రూపంలో \(\vec{\tau}=\overrightarrow{\mathrm{P}} \times \overrightarrow{\mathrm{r}}\) ఇక్కడ E ఏకరీతిగా ఉండును.

→ విద్యుత్ ద్విధ్రువంను విద్యుత్ క్షేత్రంలో ఉన్నప్పుడు స్థితిజ శక్తి
U = -PE cos θ = \(-\overrightarrow{\mathrm{P}} \cdot \overrightarrow{\mathrm{E}}\)

→ గాస్ సిద్ధాంతం, \(\oint \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}=\frac{\mathrm{q}}{\varepsilon_0}\)

→ ఏదైనా బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత

• రేఖీయ ఆవేశం వల్ల, E = \(\frac{1}{2 \pi \varepsilon_0} \cdot \frac{\lambda}{r}\)
• అనంత ఆవేశ తలపలక వల్ల సాంద్రత, E = \(\frac{\sigma}{2 \varepsilon_0}\)
• నిర్ణీత మందం ఉన్న అనంత సమతల వాహకం వల్ల, E = \(\frac{\sigma}{2 \varepsilon_0}\)

→ రెండు అనంత సమాంతర పలకల ఆవేశాల వల్ల విద్యుత్ క్షేత్ర తీవ్రత

• రెండు పలకల మధ్య ప్రాంతంలో E = \(\frac{1}{2 \varepsilon_0}\)(σ_A – σ_B)
• రెండు పలకల వెలుపల ప్రాంతంలో E = \(\frac{2}{2 \varepsilon_0}\)(σ_A + σ_B)

→ ఆవేశ గోళాకార కర్పరము వల్ల

• కర్పరం లోపల, బిందువు ఉన్నప్పుడు E = 0
• కర్పరం వెలుపల, బిందువు ఉన్నప్పుడు E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}^2}\)
• కర్పరంపైన, E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}^2}\)

→ ఆవేశ గోళం వల్ల విద్యుత్ క్షేత్ర తీవ్రత,

• బిందువు వెలుపల ఉన్నప్పుడు, E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{\mathrm{q}}{\mathrm{r}^2}=\frac{\rho}{\varepsilon_0} \cdot \frac{\mathrm{R}^3}{\mathrm{r}^2}\)
• బిందువు గోళంపై ఉన్నప్పుడు, E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{R^2}=\frac{\rho R}{3 \varepsilon_0}\)
• బిందువు గోళం లోపల ఉన్నప్పుడు, E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{\mathrm{qr}}{\mathrm{R}^3}=\frac{\rho \mathrm{r}}{3 \varepsilon_0}\)

Students can go through AP Inter 2nd Year Physics Notes 3rd Lesson తరంగ దృశాశాస్త్రం will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 3rd Lesson తరంగ దృశాశాస్త్రం

→ తరంగ దృశాశాస్త్రం ప్రకారం విద్యుదయస్కాంత తరంగాలు.

→ ఒకే దశలో డోలనాలు చేసే బిందువుల బిందుపథాన్ని తరంగాగ్రం అంటారు. అంటే స్థిరమైన దశ గల ఉపరితలాన్ని తరంగాగ్రం అంటారు.

→ రెండు కాంతి తరంగాలు అధ్యారోపణం చెందుటవల్ల యానకంలో శక్తి ఏకరీతిగా వితరణ చెందదు. దీనిని వ్యతికరణం అంటారు.

→ ఒకే పౌనఃపున్యము (లేదా) తరంగదైర్ఘ్యము మరియు స్థిరదశాభేదము గల రెండు కాంతి జనకాలను సంబద్ధ జనకాలు అంటారు.

→ నిర్మాణాత్మక వ్యతికరణంలో రెండు జనకాల మధ్య పథ భేదము λ కు పూర్ణాంక గుణిజాలుగా ఉంటుంది.

→ వినాశాత్మక వ్యతికరణంలో రెండు జనకాల మధ్య పథ భేదము \(\frac{\lambda}{2}\) కు బేసి గుణిజాలుగా ఉంటుంది.

→ వ్యతికరణ నమూనాలో చీకటి మరియు వెలుగు పట్టీలు ఒకే మందము కలిగి ఉంటాయి. యంగ్ జంట చీలికల ప్రయోగంలో, పట్టీలు అతిపరావలయ ఆకారంలో ఉంటాయి.

→ యంగ్ జంట చీలికల ప్రయోగంలో, స్వల్ప వ్యతికరణ నమూనాలో పట్టీలు తిన్నగా ఉంటాయి.

→ కాంతి అడ్డు యొక్క అంచుల వద్ద వంగి, జ్యామితీయచ్ఛాయా ప్రదేశంలోకి ప్రవేశిస్తుంది. ఈ దృగ్విషయాన్ని వివర్తనం అంటారు.

→ ఏకచీలిక వివర్తనంలో, అన్ని గౌణ గరిష్ఠాలు మరియు కనిష్టాలు ఒకే మందము కలిగి ఉంటాయి.

→ ఏకచీలిక వివర్తనంలో కేంద్ర గరిష్ఠం మందము, ఏదైనా గౌణ గరిష్ఠం (లేదా) కనిష్ఠం మందానికి రెట్టింపు ఉంటుంది.

→ దృశాపరికరాల దృక్ సామర్థాన్ని వివర్తనం ద్వారా తెలుసుకోవచ్చును.

→ కేవలం తిర్యక్ తరంగాల వల్ల మాత్రమే ద్రువణం సాధ్యమవుతుంది.

→ జనకం నుండి వచ్చు సాధారణ కాంతి అధ్రువిత కాంతి.

→ కాంతి కంపనాలు కేవలం ఒకే తలానికి మాత్రమే పరిమితమైతే దానిని ధ్రువణం అంటారు.

→ కాంతి కిరణము ధ్రువణ కోణముతో పతనమైతే, పరావర్తన కిరణము, వక్రీభవన కిరణానికి లంబంగా ఉంటుంది.

→ చీలిక నుండి తెర వరకు గల దూరాన్ని ఫ్రెనెల్ దూరం అంటారు.

→ రెండు బిందు వస్తువులు వేరు చేసినట్లుగా కనిపించినప్పుడు, వాటిమధ్య స్వల్ప దూరాన్ని (రేఖీయ (లేదా) కోణీయ) పృథఃక్కరణ అవధి అంటారు.

→ పృథఃక్కరణ అవధి యొక్క ఉత్రమాన్ని పృధఃక్కరణ సామర్థ్యం అంటారు.

→ బ్రూస్టర్ కోణము యొక్క టాంజెంట్ విలువ యానకం వక్రీభవన గుణకానికి సమానం. μ = tan i_p. దీనిని బ్రూస్టర్ నియమం అంటారు.

→ విశ్లేషణకారి గుండా పోయే ధ్రువత కాంతి తీవ్రత, విశ్లేషణకారి మరియు ధ్రువణకారి మధ్యగల కొసైన్ కోణానికి అనులోమానుపాతంలో ఉంటుంది. దీనిని మాలస్ నియమం అంటారు.
I ∝ cos²θ

→ దశా భేదము = \(\frac{2 \pi}{\lambda}\) × పథ భేదము

→ గరిష్ట తీవ్రత నిబంధన, Φ = 2nπ

→ కనిష్ఠ తీవ్రత నిబంధన, Φ = (2n + 1)π

→ పథ భేదము S₂P – S₁P = nλ(గరిష్ఠం)
S₂P – S₁P = (2n + 1)\(\frac{\lambda}{2}\) (కనిష్టం)

→ ఫ్రెనెల్ దూరము (Z_F) = \(\frac{\mathrm{a}^2}{\lambda}\)

→ వెలుగుపట్టీ స్థానము (x_n) = \(\frac{\mathrm{n} \lambda \mathrm{D}}{\mathrm{d}}\)

→ చీకటిపట్టీ స్థానము (x) = (2n + 1)\(\frac{\lambda D}{d}\)

→ దూరదర్శిని యొక్క పృథఃక్కరణ సామర్థ్యము = \(\frac{1}{\mathrm{~d} \theta}=\frac{\mathrm{D}}{1.22 \lambda}\)

→ సూక్ష్మదర్శిని యొక్క పృథఃక్కరణ సామర్థ్యము = \(\frac{1}{d}=\frac{2 \mu \sin \theta}{\lambda}\)

→ బ్రూస్టర్ నియమం, μ = Tan i_B

→ మాలస్ నియమం I = I₀ cos²θ

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 7 నిశ్చిత సమాకలనులు Exercise 7(c) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 7 నిశ్చిత సమాకలనులు Exercise 7(c)

అభ్యాసం – 7 (సి)

I. క్రింది సమాకలనులను గణించండి.

ప్రశ్న 1.
\(\int_0^{\pi / 2} \sin ^{10} x d x\)
సాధన:
\(\frac{9}{10}\).\(\frac{7}{8}\).\(\frac{5}{6}\).\(\frac{3}{4}\).\(\frac{1}{2}\).\(\frac{\pi}{2}\) = \(\frac{63 \pi}{512}\)

ప్రశ్న 2.
\(\int_0^{\pi / 2} \cos ^{11} x d x\)
సాధన:
n బేసి సంఖ్య

ప్రశ్న 3.
\(\int_0^{\pi / 2}\) cos⁷ x sin² x dx
సాధన:
I = \(\int_0^{\pi / 2}\) cos⁷ x sin² x dx
= \(\int_0^{\pi / 2}\)sin^mx.cosⁿ x dx
m – సరి సంఖ్య
n – బేసి సంఖ్య
= \(\frac{n-1}{m+n}\).\(\frac{n-3}{m+n-2}\)….\(\frac{2}{m+3}\).\(\frac{1}{m+1}\)
= \(\frac{7-1}{9}\) × \(\frac{7-3}{9}\) × \(\frac{7-5}{5}\) × \(\frac{1}{2+1}\)
= \(\frac{6}{9}\) . \(\frac{4}{7}\) . \(\frac{2}{5}\) . \(\frac{1}{3}\) = \(\frac{16}{315}\)

ప్రశ్న 4.
\(\int_0^{\pi / 2} \sin ^4 x \cos ^4 x d x\)
సాధన:
\(\int_0^{\pi / 2} \sin ^m x \cdot \cos ^n x d x\)
m, n లు సరిసంఖ్యలు

ప్రశ్న 5.
\(\int_0^\pi\) sin³ x cos⁶ x dx
సాధన:
= \(\int_0^\pi\) sin² x cos⁶ x dx
= \(\int_0^\pi\)(1 – cos²x) . cos⁶x. sin x dx
cos x = t cos π = -1
-sin x dx = dt cos 0 = 1

ప్రశ్న 6.
\(\int_0^{2 \pi}\) sin² x cos⁴ x dx
సాధన:
sin² x . cos⁴ x dx సరి ప్రమేయము

ప్రశ్న 7.
\(\int_{-\pi / 2}^{\pi / 2} \sin ^2 \theta \cos ^7 \theta d \theta\)
సాధన:
sin² θ . cos⁷ θ సరి ప్రమేయము
f(θ) = sin² θ . cos⁷ θ dθ
f(-θ) = sin²(-θ) . cos⁷(-θ)
= f(θ)
= 2\(\int_0^{\pi / 2}\) sin² θ . cos⁷ θ dθ
\(\int_0^{\pi / 2}\) sin^mx.cosⁿx dx
n బేసి సంఖ్య, n = 7

ప్రశ్న 8.
\(\int_{-\pi / 2}^{\pi / 2}\) sin³θ cos³θ dθ
సాధన:
f(θ) = sin³θ . cos³θ
f(-θ) = sin³(-θ) cos³(-θ)
= sin³θ cos³ θ = -f(θ)
f(θ) బేసి ప్రమేయము
∴ \(\int_{-\pi / 2}^{\pi / 2}\)sin³θ . cos³θ dθ = 0

ప్రశ్న 9.
\(\int_0^a x\left(a^2-x^2\right)^{\frac{7}{2}} d x\)
సాధన:
x = a sin θ అనుకొనుము. a = a sin θ
dx = a cos θ dθ θ = π/2

ప్రశ్న 10.
\(\int_0^2 x^{3 / 2} \sqrt{2-x} d x\)
సాధన:
x = 2 cos² θ
dx = 4 cos θ sin θ dθ

II. క్రింది సమాకలనులను గణించండి.

ప్రశ్న 1.
\(\int_0^1 x^5(1-x)^{5 / 2} d x\)
సాధన:
x = – sin² θ
dx = 2 sin θ . cos θ . dθ

ప్రశ్న 2.
\(\int_0^4\)(16 – x²)^5/2 dx
సాధన:
x = 4 sin θ 4 = 4 sin θ
dx = 4 cos θ dθ sin θ = 1
θ = π/2
I = \(\int_0^{\pi / 2}\) (16 – 16sin²θ)^5/2 . 4 cos θ dθ

ప్రశ్న 3.
\(\int_{-3}^3\) (9 – x²)^3/2 x dx
సాధన:
Let f(x) = \(\left(9-x^2\right)_x^{3 / 2}\)
f(x) = (9 – (-x²))^3/2 (-x)
= (9 – x²)^3/2 . x
= f(-x)
∴ f బేసి ప్రమేయము
∴ \(\left(9-x^2\right)^{3 / 2}. x d x\) = 0

ప్రశ్న 4.
\(\int_0^5\) x³(25 – x²)^7/2 dx
సాధన:
I = \(\int_0^5\)x³(25 – x²)^7/2 dx అనుకొనుము
x = 5 sin θ
dx = 5 cos θ dθ

ప్రశ్న 5.

సాధన:
f(x) = sin⁸x. cos⁷ x అనుకొనుము
f(-x) = sin⁸(-x) . cos⁷(-x) = sin⁸x. cos⁷x
∴ f సరి ప్రమేయం

ప్రశ్న 6.
\(\int_3^7 \sqrt{\frac{7-x}{x-3}} d x\)
సాధన:
x = 3 cos² θ + 7 sin² θ
dx = (7 – 3) sin 2θ dθ
dx = 4 sin 2θ dθ
ఎగువ హద్దు :
x = 3 cos² θ + 7 sin² θ
7 = 3 cos² θ + 7 sin² θ
4 cos² θ = 0
cos θ = 0
θ = \(\frac{\pi}{2}\)

దిగువ హద్దు
x = 3 cos² θ + 7 sin² θ
3 = 3 sin² θ + 7 sin² θ
4 sin² θ = 0
sin θ = 0
θ = 0
7 – x = 7 – (3 cos²θ + 7 sin² θ)
= (7 – 3) cos²θ
= 4 cos²θ
x – 3 = 3 cos²θ + 7 sin² θ – 3
= (7 – 3) sin²θ
= 4 sin²θ

ప్రశ్న 7.
\(\int_2^6 \sqrt{(6-x)(x-2)} d x\)
సాధన:
x = 2 cos²θ + 6 sin²θ
dx = (6 – 2) sin 2θ dθ
dx = 4 sin 2θ dθ

ఎగువ హద్దు :
x = 2 cos²θ + 6 sin²θ
6 = 2 cos²θ + 6 sin²θ
4 cos²θ = 0
cos θ = 0
θ = \(\frac{\pi}{2}\)

దిగువ హద్దు:

x = 2 cos²θ + 6 sin²θ
2 = 2 cos²θ + 6 sin²θ
4 sin²θ = 0
θ = 0
6 – x = 6 – (2 cos²θ + 6 sin²θ)
= (6 – 2) cos²θ
= 4 cos²θ
x – 2 = 2 cos²θ + 6 sin²θ – 2
= (6 – 2)sin²θ
= 4 sin²θ

ప్రశ్న 8.
\(\int_0^{\pi / 2}\)tan⁵x cos⁸x dx
సాధన:

III. దిగువ సమాకలనులను సాధించండి.

ప్రశ్న 1.
\(\int_0^1\)x^7/2(1 – x)^5/2 dx
సాధన:
x = sin²θ
dx = 2 sin θ cos θ dθ

ప్రశ్న 2.
\(\int_0^\pi\) (1 + cos x)³ dx
సాధన:
\(\int_0^\pi\) (1 + cos x)³ dx
= \(\int_0^\pi\)(2 cos²\(\frac{x}{2}\))³ dx
= \(\int_0^\pi\) 2³. cos⁶ \(\frac{x}{2}\) dx
\(\frac{x}{2}\) = t ⇒ dx = 2 dt

ఎగువ హద్దు : ⇒ x = π ⇒ \(\frac{\pi}{2}\) = t
దిగువ హద్దు : ⇒ x = 0 ⇒ 0 = t
= 8 \(\int_0^{\pi / 2}\) cos⁶ 6(2 dt)

ప్రశ్న 3.
\(\int_4^9 \frac{d x}{\sqrt{(9-x)(x-4)}}\)
సాధన:
x = 4 cos²θ + 9 sin²θ
dx = (9 – 4) sin 2θ dθ
dx = 5 sin 2θ dθ
ఎగువ హద్దు :
x = 4 cos²θ + 9 sin²θ
9 = 4 cos²θ + 9 sin²θ
5 cos²θ = 0
θ = \(\frac{\pi}{2}\)
దిగువ హద్దు :
x = 4 cos²θ + 9 sin²θ
4 = 4 cos²θ + 9 sin²θ
5 sin²θ = o
θ = 0
9 – x = 9 – (4 cos²θ + 9 sin²θ)
= (9 – 4) cos²θ
= 5 cos²θ
x – 4 = 4 cos²θ + 9 sin²θ – 4
= (9 – 4)sin²θ
= 5 sin²θ

ప్రశ్న 4.
\(\int_0^5 x^2(\sqrt{5-x})^7 d x\)
సాధన:
x = 5 sin² θ
dx = 10 sinθ cos θ dθ

ప్రశ్న 5.
\(\int_0^{2 \pi}\) (1 + cos x)⁵ (1 – cos x)³ dx.
సాధన:

Students can go through AP Inter 2nd Year Physics Notes 2nd Lesson కిరణ దృశాశాస్త్రం, దృగ్ సాధనాలు will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 2nd Lesson కిరణ దృశాశాస్త్రం, దృగ్ సాధనాలు

→ కాంతి ఒక శక్తి రూపము. ఇది కంటిపై పడినప్పుడు మనకు దృశా జ్ఞానాన్ని కలిగిస్తుంది.

→ దృగ్గోచర కాంతిని గూర్చి దృశా శాస్త్రంలో అధ్యయనం చేస్తారు.

→ పరావర్తనాన్ని నునుపు తలం నుండి (లేదా) గరకు తలాలు గోడలు, నేల మొదలగు వాటి నుండి పొందవచ్చు.

→ ఎడారులలో ఎండమావులు ఏర్పడుట దృశా ఉదాహరణ.

→ నిజ ప్రతిబింబాలు ఎల్లప్పుడూ తలక్రిందులుగా మరియు మిథ్యా ప్రతిబింబాలు ఎల్లప్పుడూ నిలువుగా ఏర్పడతాయి.

→ పుటాకార దర్పణం ఏర్పరచే ప్రతిబింబం, నాభిని దాటి ఏర్పడదు.

→ పుటాకార దర్పణంలో f మరియు R రెండింటిని ధనాత్మకంగా తీసుకుంటాం.

→ కుంభాకార దర్పణంలో f మరియు R రెండింటిని రుణాత్మకంగా తీసుకుంటాం.

→ నిజ వస్తువులు మరియు నిజ ప్రతిబింబాల దూరాలను రుణాత్మకంగా తీసుకుంటాం.

→ మిథ్యా వస్తువులు మరియు మిథ్యా ప్రతిబింబాల దూరాలను ధనాత్మకంగా తీసుకుంటాం.

→ దర్పణం ఏర్పరచే ప్రతిబింబం నిజ ప్రతిబింబమైతే ఆవర్థనం రుణాత్మకం.

→ దర్పణం ఏర్పరచే ప్రతిబింబం మిథ్యా ప్రతిబింబమైతే ఆవర్థనం ధనాత్మకం.

→ ఉష్ణోగ్రత పెరిగితే వక్రీభవన గుణకము తగ్గుతుంది.

→ మంద కటకానికి నాభ్యంతరము తక్కువగా ఉంటుంది.

→ కాంతి కిరణము వక్రీభవన యానకంపై లంబంగా పతనం చెందినప్పుడు స్నేల్ నియమం విఫలమవుతుంది.

→ స్నేల్ నియమం ప్రకారం, పతన కోణము సైన్ విలువకు, వక్రీభవన కోణం సైన్ విలువకుగల నిష్పత్తి, వక్రీభవన గుణకానికి సమానం.

→ దర్పణం యొక్క వ్యాసాన్ని, దర్పణం ద్వారం అంటారు.

→ గోళాకార దర్పణం మధ్యబిందువును ధ్రువం అంటారు.

→ ధ్రువం మరియు దర్పణం యొక్క వక్రత కేంద్రములను కలిపే రేఖను ప్రధానాక్షం అంటారు.

→ గోళం యొక్క వ్యాసార్థముతో, దానిలో భాగంగా దర్పణం ఏర్పడితే దానిని వక్రతా వ్యాసార్థం అంటారు.

→ దర్పణం ధ్రువం నుండి ప్రధాన నాభి వరకుగల దూరాన్ని నాభ్యంతరము అంటారు.

→ కథకంపైబడే కాంతిని అభిసరణ (లేదా) అపసరణ చెందించే సామర్థ్యాన్ని కటకం యొక్క సామర్థ్యం అంటారు.

→ వర్షం పడిన తర్వాత సూర్యుడి నుండి వచ్చే తెల్లని కాంతి ఏర్పరచే వర్ణపటం ఇంద్రధనస్సువలె ఏర్పడుతుంది.

→ తెల్లని కాంతి వేరువేరు రంగులుగా విడిపోయే దృగ్విషయాన్ని కాంతి విక్షేపణం అంటారు.

→ హ్రస్వ దృష్టిగల వ్యక్తి దగ్గర వస్తువులను స్పష్టంగా చూడగలడు మరియు దూరపు వస్తువులను స్పష్టంగా చూడలేడు.

→ దీర్ఘ దృష్టిగల వ్యక్తి దూరపు వస్తువులను స్పష్టంగా చూడగలడు మరియు దగ్గర వస్తువులను స్పష్టంగా చూడలేడు.

→ పుటాకార దర్పణం నాభ్యంతరము (f) = \(\frac{R}{2}\)

→ దరణ సూత్రం \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)

→ రేఖీయ ఆవర్థనం (m) = \(\frac{I}{o}=\frac{-v}{u}=\frac{f}{f-u}=\frac{f-v}{f}\)

→ స్నేల్ సూత్రం, \(\frac{\sin \mathrm{i}}{\sin \mathrm{r}}\) = μ

→ యానకం వక్రీభవన గుణకం (µ) = \(\frac{c}{v}\)

→ µ = \(\frac{\mu_2}{\mu_1}\), µ₂ = \(\frac{1}{{ }_2 \mu_1}\)

→ µ = \(\frac{1}{\sin c}\)

→ \(\frac{-1}{\mathrm{u}}+\frac{\mu}{\mathrm{v}}=\frac{\mu-1}{\mathrm{R}}\)

→ కటక తయారీదారు సూత్రం \(\frac{1}{f}\) = (µ – 1)\(\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)

→ కటక సూత్రం \(\frac{-1}{u}+\frac{1}{v}=\frac{1}{R}\)

→ పుటాకార (లేదా) కుంభాకార కటకం రేఖీయ ఆవర్థనం m = \(\frac{I}{o}=\frac{v}{u}=\frac{f}{f+u}=\frac{f-v}{f}\)

→ కటకం యొక్క సామర్థ్యం (P)

→ రెండు కటకాలు స్పర్శలో ఉంటే, \(\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{f}_1}+\frac{1}{\mathrm{f}_2}\)

→ రెండు కటకాలు కొంత దూరంలో ఉన్నప్పుడు, \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}-\frac{d}{f_1 f_2}\)

→ నమ కటకం సామర్థ్యముP = P₁ + P₂(రెండూ స్పర్శలో)P = P₁ + P₂ – dP₁P₂(కొంత దూరంలో ఉన్నప్పుడు)

→ వక్రీభవన గుణకము (µ) = \(\frac{\sin \left(\frac{A+D_m}{2}\right)}{\sin A / 2}\)

→ విక్షేపణ సామర్థ్యము (ω) = \(\frac{\delta_{\mathrm{v}}-\delta_{\mathrm{R}}}{\delta}=\frac{\mu_{\mathrm{v}}-\mu_{\mathrm{r}}}{\mu-1}\)

→ సరళ సూక్ష్మదర్శిని ఆవర్థన సామర్థ్యము (m) = 1 + \(\frac{D}{f}\).

→ సంయుక్త సూక్ష్మదర్శిని ఆవర్ధన సామర్థ్యము (m) = \(\frac{\mathrm{v}_0}{\mathrm{u}_0}\left(1+\frac{\mathrm{D}}{\mathrm{f}_0}\right)=\frac{-\mathrm{L}}{\mathrm{f}_0}\left(1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\right)\)

Students can go through AP Inter 2nd Year Physics Notes 1st Lesson తరంగాలు will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 1st Lesson తరంగాలు

→ పదార్థము వాస్తవంగా కదలకుండా అలజడులను (శక్తులను) ప్రసారం చేసే వానిని తరంగాలు అంటారు.

→ యానకం కణాల కంపనాల ద్వారా శక్తి ప్రసారము జరిగే ప్రక్రియను తరంగ చలనం అంటారు.

→ తరంగం ప్రసార దిశకు యానకం కణాలు లంబంగా కంపిస్తే, వాటిని తిర్యక్ తరంగాలు అంటారు.

→ తరంగం ప్రసార దిశకు యానకం కణాలు సమాంతరంగా కంపిస్తే, వాటిని అనుదైర్ఘ్య తరంగాలు అంటారు.

→ కుడివైపు చలించు, పురోగామి తరంగ సమీకరణం y = a (sin ot – kx). ఇక్కడ x = స్థానభ్రంశం, ω = కోణీయ స్థానభ్రంశం, t = కాలం, k = తరంగ స్థిరాంకము.

→ తరంగాల అధ్యారోపణ నియమము : “రెండు లేదా అంతకన్నా ఎక్కువ తరంగాలు ఒకే దిశలో చలిస్తూ కలిస్తే, వాని ఫలిత స్థానభ్రంశం మొత్తం తరంగాల విడివిడి స్థానభ్రంశాల బీజీయ మొత్తంనకు సమానం.

→ తరంగాల అధ్యారోపణ సూత్రం, వ్యతికరణం, వివర్తనం, స్థిర తరంగాలు మరియు విస్పందనాలను వివరిస్తుంది.

→ యానకం చివర నుండి పురోగామి తరంగాలు పరావర్తనం చెందుతాయి. పరావర్తనం ఒక దృఢమైన సరిహద్దు వద్ద జరిగితే, పతన మరియు పరావర్తన తరంగాల మధ్య దశాభేదం 7 కు సమానం. తెరిచిన సరిహద్దు వద్ద పరావర్తన జరిగితే, పతన మరియు పరావర్తన తరంగాలు ఒకే దిశలో ఉంటాయి.

→ ఒకే కంపన పరిమితి మరియు పౌనఃపున్యం ఉన్న పతన మరియు పరావర్తన తరంగాలు పొడవుగల తీగవెంట వ్యతిరేక దిశలలో కలిస్తే, ఫలితంగా స్థిర తరంగం ఏర్పడును.

→ కంపిస్తున్న తీగ పౌనఃపున్యం v = \(\frac{\mathrm{P}}{2 l} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}\)

→ శూన్య కంపన పరిమితి స్థానాలను అస్పందనాలు అంటారు.

→ గరిష్ఠ కంపన పరిమితి స్థానాలను ప్రస్పందనాలు అంటారు.

→ వ్యవస్థలో సాధ్యమయ్యే తక్కువ సహజ పౌనఃపున్యంను ప్రాథమిక రీతి లేక మొదటి అనుస్వరం అంటారు.

→ బాహ్య పౌనఃపున్యం, సహజ పౌనఃపున్యంనకు దగ్గరగా ఉంటే అనునాదం ఏర్పడుతుంది.

→ T తన్యత, రేఖీయ సాంద్రత ఉన్న తంత్రి వేగం υ = \(\sqrt{\frac{\mathrm{T}}{\mu}}\)

→ B ఆయత గుణకం, p సాంద్రత ఉన్న ప్రవాహిలో ధ్వని వేగం, υ = \(\sqrt{\frac{B}{\rho}}\)

→ లోహ కడ్డీలో అనుదైర్ఘ్య తరంగాల వేగం, υ = \(\sqrt{\frac{Y}{\rho}}\)

→ రెండు వరుస అస్పందనాలు లేక ప్రస్పందనాల మధ్య దూరం కు సమానం.

→ రెండువైపులా దృఢంగా బిగించిన L పొడవుగల సాగదీసిన తీగ పౌనఃపున్యాలు v = \(\frac{\mathrm{nv}}{2 \mathrm{~L}}\), n = 1,2, 3, ……….

→ ఒకవైపు మూసి మరియొక వైపు తెరిచి ఉన్న L పొడవుగల గొట్టం పౌనఃపున్యాలు, v = \(\frac{\mathrm{nv}}{2 \mathrm{~L}}\) n = 1,2, 3, ……….

→ ఒక వస్తువును కంపింపచేసి, స్వేచ్ఛగా వదిలితే, అది చేసే కంపనాలను “సహజ కంపనాలు” అంటారు.

→ ఒక వస్తువు బాహ్య ఆవర్తన బల కంపనాల ప్రభావంతో కంపిస్తే, ఆ కంపనాలను బలాత్కృత కంపనాలు అంటారు.

→ సమీప పౌనఃపున్యాలు గల రెండు హరాత్మక ధ్వని తరంగాలు ఒకే దిశలో వ్యతికరణం చెంది, క్రమ ఆవర్తన కాలంలో ధ్వని వృద్ధి మరియు క్షీణత ఉన్న ధ్వనిని వింటాము. ఈ దృగ్విషయంను విస్పందనాలు అంటారు.

→ ధ్వని జనకం మరియు పరిశీలకుల మధ్య సాపేక్ష చలనం ఉంటే, పరిశీలకుడు వినే దృశ్య పౌనఃపున్యంలోని మార్పును డాప్లర్ ప్రభావం అంటారు.

→ యానకంలో ధ్వని వేగం, v = υλ ఇక్కడ v = \(\frac{1}{T}\)

→ తరంగ వేగం, υ = \(\frac{\omega}{\mathbf{k}}\)

→ తరంగ ప్రసార స్థిరాంకము, K = \(\frac{2 \pi}{\lambda}\)

→ కోణీయ వేగం ω = \(\frac{2 \pi}{\mathrm{T}}\) = 2πυ

→ ధన X-అక్షం దిశలో పురోగామి తరంగ సమీకరణం y = a.sin (ωt – kx). రుణ x అక్షం దిశలో y = a sin(ωt +kx)

→ అధ్యారోపణ సూత్రం నుండి ఫలిత తరంగం y = y₁ + y₂

→ స్థిర తరంగ సమీకరణం y = 2a sin kx cos ωt లేక y = 2a cos kx sin ωt.

→ సాగదీసిన తంత్రి లేక తీగలో

• తిర్యక్ కంపనాల వేగం υ = \(\sqrt{\frac{\mathrm{T}}{\mu}}\)
• ప్రాథమిక పౌనఃపున్య కంపనము, υ₀ = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)
• అనుస్వరాల పౌనఃపున్యం, υ_p = \(\frac{\mathrm{P}}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\) ఇక్కడ P అనుస్వరాల సంఖ్యను తెల్పుతుంది.

→ వేర్వేరు యానకంలలో న్యూటన్స్ ధ్వనివేగ సమీకరణము

• ఘన పదార్థంలో υ_s = \(\sqrt{\frac{Y}{\rho}}\)
• ద్రవ పదార్థంలో υ_l = \(\sqrt{\frac{K}{\rho}}\)
• వాయువులలో υ_g = \(\sqrt{\frac{\mathrm{P}}{\rho}}\)

→ వాయువులలో లాప్లాస్ ధ్వని వేగం ఫార్ములా
Y = ఘనపదార్థం యంగ్ గుణకం υ_g = \(\sqrt{\frac{\gamma \mathbf{P}}{\rho}}\)
k = ద్రవాల ఆయుత గుణకం మరియు P = వాయు పీడనం.

→ మూసిన గొట్టంలో

• ప్రాథమిక పౌనఃపున్యం వద్ద గొట్టం పొడవు l = \(\frac{\lambda}{4}\) ⇒ λ = 4l
• ప్రాథమిక పౌనఃపున్య కంపనము, v = \(\frac{v}{\lambda}=\frac{v}{4 l}\)
• మూసిన గొట్టంలో బేసి అనుస్వరాలను సపోర్టు చేయును. అనుస్వరాల పౌనఃపున్యాల నిష్పత్తి 1:3:5: ….. etc

→ తెరిచిన గొట్టంలో

• ప్రాథమిక పౌనఃపున్యం వద్ద గొట్టం పొడవు, l = \(\frac{\lambda}{2}\) ⇒ λ = 2l
• ప్రాథమిక పౌనఃపున్యం కంపనం, v₀ = \(\frac{v}{\lambda}=\frac{v}{2 l}\)
• తెరిచిన గొట్టం సహజ సంఖ్యల అనుస్వరాలను సపోర్టు చేస్తుంది. అనుస్వరాల పౌనఃపున్యాల నిష్పత్తి 1:2:3: ……….. etc

→ విస్పందనాల పౌనఃపున్యం ΔV = v₁ – v₂

→ డాప్లర్ ప్రభావ సాధారణ సమీకరణం, v’ = \(\left[\frac{v \pm v_0}{v \pm v_s}\right]\)v

→ యానకం ధ్వని వేగం (v) ను పరిగణనలోకి తీసుకుంటే, దృశ్య పౌనఃపున్యం
v’ = \(\left[\frac{v \pm v_0 \pm v_m}{v \pm v_s \pm v_m}\right]\)v సంజ్ఞ సంప్రదాయం పాటిస్తుంది.

Students can go through AP Inter 2nd Year Botany Notes 5th Lesson మొక్కలలో శ్వాసక్రియ will help students in revising the entire concepts quickly.

AP Inter 2nd Year Botany Notes 5th Lesson మొక్కలలో శ్వాసక్రియ

→ మనం ‘ఆహారం’ అని పిలిచే స్థూల అణువులు ఆక్సీకరణం చెందినప్పుడు ‘జీవ’ చర్యలకు కావలసిన శక్తి లభిస్తుంది.

→ హరిత మొక్కలు, సయనోబాక్టీరియమ్లు మాత్రమే తమ స్వంత ఆహారాన్ని తయారు చేసుకుంటాయి.

→ కణంలో ఆక్సీకరణ జరిగినప్పుడు ఆహారంలో ఉండే శక్తి అంతా ఒకేసారి విడుదలకాదు. ఎన్ఎమ్ల నియంత్రణలో

→ జరిగే చర్యల వల్ల శక్తి అంచెలంచెలుగా విడుదలై ATP రూపంలో నిల్వచేయబడుతుంది.

→ కణ ఆక్సీకరణలో తోడ్పడే పదార్థాలను శ్వాసక్రియాధస్థ పదార్థాలు అంటారు.

→ ATP ని కణశక్తి నగదు అంటారు.

→ శ్వాసక్రియ 2 రకాలు

• వాయుసహిత,
• అవాయు శ్వాసక్రియ.

→ వాయుసహిత శ్వాసక్రియ 2 సమక్షంలో 4 దశలుగా జరుగుతుంది.

→ గ్లూకోస్ విచ్ఛిన్నం చెంది 2 PAలుగా మారే క్రమాన్ని గ్లైకాలిసిస్ లేదా EMP పథం అంటారు.

→ పైరువిక్ ఆమ్లం పూర్తిగా ఆక్సీకరణం చెంది, హైడ్రోజన్ ను తొలగించి, 300, అణువులను ఏర్పరుస్తుంది.

→ పైరువిక్ ఆమ్లం ఆక్సీకరణ డీకార్టాక్సిలేషన్ చెంది పైరువిక్ డీహైడ్రోజినేజ్ సమక్షంలో కోఎన్జైమ్ – ఎ తో సంగ్రహణం చెంది అసిటైల్ కో. ఎన్జైమ్ A ఏర్పడుతుంది.

→ అసిటైల్ కో ఎన్జైమ్ A సంపూర్ణ ఆక్సీకరణం చెందిన శక్తిని NADPH + H⁺ రూపంలో క్రెబ్స్ వలయం ద్వారా విడుదల చేస్తుంది.

→ NADPH + H⁺, FADH₂ లు ఆక్సీకరణం చెంది విడుదలైన ఎలక్ట్రాన్లు, ETS ద్వారా 1/2 O₂ ను చేరి 1నీటి అణువును ఏర్పరుస్తాయి.

→ ATP సంశ్లేషణను పీటర్ మిట్చెల్ కెమీఆస్మాటిక్ సిద్ధాంతం ద్వారా వివరించవచ్చు.

→ 1 గ్లూకోస్ ఆక్సీకరణం చెంది 36 ATPలు ఏర్పడతాయి.

→ శ్వాసక్రియలో విచ్ఛిన్నక్రియ, నిర్మాణక్రియలు రెండూ కనిపిస్తాయి. కావున దానిని ఆంఫీభోలిక్పథం అంటారు.

→ శ్వాసక్రియలో అదస్థ పదార్థం ఆక్సీకరణం చెందినప్పుడు విడుదల అయిన CO₂, అణువుల సంఖ్యకు, గ్రహించబడిన O₂ అణువులకు మధ్య ఉన్న నిష్పత్తిని శ్వాసక్రియ కోషంట్ అంటారు.

→ కార్బోహైడ్రోట్ల శ్వాసక్రియ కోషంట్ – 1

→ కొవ్వుల శ్వాసక్రియ కోషంట్ – 1కన్నా తక్కువ (0.7)

→ ప్రొటీనుల శ్వాసక్రియ కోషంట్ – 1 కన్నా తక్కువ (0.9)

Students can go through AP Inter 2nd Year Botany Notes 4th Lesson ఉన్నత మొక్కలలో కిరణజన్యసంయోగక్రియ will help students in revising the entire concepts quickly.

AP Inter 2nd Year Botany Notes 4th Lesson ఉన్నత మొక్కలలో కిరణజన్యసంయోగక్రియ

→ ఆకు పచ్చని మొక్కలు కిరణజన్యసంయోగక్రియ అనే భౌతిక రసాయనిక చర్య ద్వారా కాంతిశక్తిని వాడుకుని కార్బోహైడ్రేట్లను సంశ్లేషణకు ఉపయోగించుకుంటాయి.

→ ఇది భూమి మీద ఉన్న సకల జీవులకు మూలాధారమైన ఆహారం తయారీకి, వాతావరణంలోని ప్రాణవాయువు విడుదలకు ఈ ప్రక్రియ దోహదపడుతుంది.

→ మోల్స్ అర్థ పత్రప్రయోగం ద్వారా, కిరణజన్యసంయోగక్రియకు CO₂, అవసరమని నిరూపించారు.

→ పచ్చని మొక్కలు పెరగడంలోగాలి ఆవశ్యకతను నిరూపించడానికి 1970లో జోసెఫ్ ప్రీస్ట్రీ ప్రయోగాలు చేసారు. జాన్ ఇంజన్ హౌజ్ ఒక నీటిమొక్కతో ప్రయోగాలు జరిపి, కేవలం మొక్కల ఆకుపచ్చని భాగాలే ఆక్సిజన్ ను విడుదలచేస్తాయని నిరూపించారు.

→ జూలియస్ వాన్ సాక్స్ మొడ్లల్లోని ఆకుపచ్చని భాగాలు గ్లూకోజ్ను తయారు చేస్తాయని అది పిండిపదార్థ రూపంలో నిల్వచేయబడుతుందని గుర్తించారు.

→ కిరణజన్యసంయోగక్రియలో నీటినుండి O₂ విడుదల అవుతుంది.

→ మొక్కల ఆకుపచ్చని భాగాలైన పత్రాలలోనే కాక, ఇతర ఆకుపచ్చని భాగాలలో కిరణజన్యసంయోగక్రియ జరుగుతుంది.

→ త్వచవ్యవస్థ కాంతిశక్తిని శోషించి ATP, NADPH లుగా ఏర్పడటానికి దోహదంచేస్తాయి.

→ ఆవర్ణికలో ఉన్న ఎన్జైమ్ చర్యలతో మొక్కలోకి CO₂, స్థాపించబడి, చక్కెర తయారుచేయబడి, అది పిదప పిండిపదార్థంగా మారుతుంది.

→ పత్రంలో కనిపించే రంగు ఒక వర్ణద్రవ్యం వల్ల గాక నాలుగు భిన్నమైన వర్ణద్రవ్యాల వలన కలుగుతుంది. అవి పత్రహరితం -ఎ, పత్రహరితం-బి, జాంథోఫిల్ మరియు కెరోటినాయిడ్లు.

→ వివిధ తరంగదైర్ఘ్యాల వద్ద కిరణజన్యసంయోగక్రియా రేటు తెలిపే చిత్రాన్ని చర్యవర్ణపటం అంటారు.

→ వివిధ వర్ణద్రవ్యాల కాంతిశోషణ సామర్థ్యాన్ని తెలిపే పటాన్ని శోషణ వర్ణపటము అంటారు.

→ కిరణజన్యసంయోగక్రియకు కావలసిన ముఖ్య వర్ణద్రవ్యం- పత్రహరితం

→ పత్రహరితం బి కెరోటినాయిడ్ లు జాంథోఫిల్ లును అదనపు వర్ణద్రవ్యాలు అంటారు.

→ చక్రియ కాంతి ఫాస్ఫారిలేషన్లో PS-I మాత్రమే పాల్గోంటుంది.

→ అచక్రియ కాంతి ఫాస్ఫారిలేషన్లో లో PS-I \ PS-II రెండూ పాల్గొంటాయి.

→ నీటి అణువు కాంతి సమక్షంలో నిన్నం చెంది 2Ht, 2e, 10, ఏర్పడతాయి.

→ థైలకాయిడ్ త్వచాలకిరువైపులా ప్రోటాన్ ప్రవణత ఏర్పటం వల్ల ATP సంశ్లేషణ జరుగుతుంది.

→ చక్కెర పదార్థాల తయారీకి దారితీసే ప్రక్రియలు జరగటంలో ATP – NADPH లు ఉపయోగపడతాయి. ఈ దశను జీవ సంశ్లేణ దశ అంటారు.

→ CO2 స్ధాపన లో మొదటి ఉత్పాదితము PGA (3C) అయిన, ఆ మొక్కలను C₃, మొక్కలు అంటారు. OAA (4C) అయినవాటిని C₄, మొక్కలు అంటారు.

→ క్యాన్ వలయము 3 దశలలో జరుగును.
a) కార్బాక్సిలేషన్
b) క్షయకరణ దశ
c) పునరుద్ధరణ దశ.

→ ప్రతి CO₂ అణుప్రస్థాపనకు 3ATP లు, 2NADPH లు అవసరము.

→ C₂, మొక్కలలో క్రాంజ్ అంతర్నిర్మాణం కనిపిస్తుంది. ఇవి అధిక ఉష్ణోగ్రతలను తట్టుకుంటాయి. అధికకాంతి తీవ్రతలకు ప్రతిస్పందిస్తాయి. వీటిలో కాంతి శ్వాసక్రియ జరగదు. ఎక్కువ ఉత్పత్తి జరుగుతుంది.

→ C₃, C₄, పథాలకు ప్రత్యామ్నాయంగా క్రాస్సులేసియస్ ఆమ్ల జీవక్రియా ద్వారా CO₂ స్థాపన జరుగుతుంది. ఉదా : కాక్టై (కాస్సులేసి)

→ కాంతి సమక్షంలో ఆకు పచ్చని కణజాలం O₂ ను గ్రహించి CO₂ ను విడుదల చేసే ప్రక్రియను కాంతిశ్వాస క్రియ అంటారు.

Students can go through AP Inter 2nd Year Botany Notes 3rd Lesson ఎన్జైమ్లు will help students in revising the entire concepts quickly.

AP Inter 2nd Year Botany Notes 3rd Lesson ఎన్జైమ్లు

→ అన్ని ఎన్జైమ్లు దాదాపుగా ప్రొటీనులే. కొన్ని కేంద్రకామ్లాలు ఎన్జైమ్లుగా పనిచేస్తాయి. వీటిని రైబోజైమ్లు అంటారు. 23 ‘S’ rRNA.

→ అధస్థ పదార్థము ‘S’ ఎన్జైమ్ నొక్కు లేదా సంచులుగా ఉండే క్రియాశీల స్థానానికి బంధితమై ES సంక్లిష్టం ఏర్పడుతుంది. ఈ బంధం విచ్చిన్నమై ఉత్పాదితం ‘P’ మరియు మార్పులేని ఎన్జైమ్ విడుదల అవుతాయి.

→ ES సంక్లిష్టం ఏర్పడే విధానాన్ని ఇమిల్ఫిషర్ ప్రతిపాదించిన తాళం – కప్ప, తాళం చెవి పరికల్పన, ఆ తరువాత డానియల్ ఇ-కోషాండ్ ప్రతిపాదించిన ‘ఇండ్యూస్డ్ ఫిట్ పరికల్పనలు వివరిస్తాయి.

→ ఎన్జైమ్లు ఒక నిరిష్ట ఉష్ణోగ్రత, pH ల వద్ద పనిచేస్తాయి. వాటిని యుక్తతమ ఉష్ణోగ్రత, యుక్తతమ pH అంటారు.

→ రసాయనం బందితం కావడంతోనే ఎన్జైమ్ క్రియాశీలత ఆగిపోయే విధానాన్ని నిరోధకత అంటారు. ఆ రసాయనాన్ని నిరోధకం అంటారు.

→ నిరోధకం తన అణునిర్మాణంలో అధస్థ పదార్థాన్ని దగ్గరగా పోలి ఉండి, ఎన్జైమ్ క్రియాశీలతను నిరోధిస్తే దానిని పోటీపడే నిరోధకము అంటారు.

→ నిరోధకం అధస్థపదార్థంతో నిర్మాణాత్మక పోలికను కలిగి ఉండక, క్రియాశీల స్థానం దగ్గర కాకుండా వేరేస్థానం వద్ద ఎన్జైమ్ నిరోధక సంక్లిష్టాన్ని ఏర్పరుస్తుంది. దీనిని పోటీపడని నిరోదకము అంటారు.

→ ఎన్జైమ్లను ఆరు విభాగాలుగా వర్గీకరించారు. అవి :

• ఆక్సిడోరిడక్టేజ్లు
• ట్రాన్స్ ఫరేజ్లు
• హైడ్రోలేజ్లు
• లయేజ్లు
• ఐసోమరేజ్లు
• లైగేజ్లు

→ గ్లూకోజ్ – 6 – ఫాస్ట్రోట్రాన్స్ఫరేజ్ కు ఎన్జైమ్ సంఖ్య 2.7.1.2. దీనిలో మొదటి సంఖ్య ఎన్జైమ్ విభాగమును, రెండో సంఖ్య ఎన్జైమ్ ఉపవిభాగమును, మూడో సంఖ్య ఉప-ఉప విభాగమును, నాలుగో సంఖ్య ఎన్జైమ్ వరుస సంఖ్యను తెలియచేస్తుంది.

→ ఎన్జైమ్లోని ప్రొటీను భాగాన్ని అవోఎన్జైమ్ అని, ప్రొటీను కాని భాగమును సహకారము అని అంటారు.

→ అపోఎన్జైమ్కు వదులుగా బందితమైన సేంద్రియ సహకారకాలను సహ ఎన్జైమ్లు అంటారు.

→ అపో ఎన్జైమ్కు గట్టిగా బందితమైన ఉన్న సేంద్రియ పదార్థాలను ప్రాస్థటిక్ సమూహాలు అంటారు.

→ వివిధ రకాల ఎన్జైమ్లు పాల్గోనే ఉత్ప్రేరక చర్యల్లో సహ ఎన్జైమ్ల అవశ్యక రసాయన అనుఘటకాలు విటమిన్లుగా ఉంటాయి.
ఉదా : NAD, NADP లు రెండు నియాసిన్లను కలిగి ఉంటాయి.

→ కార్టాక్సి పెద్డడేజ్కి జింక్ ఒక సహకారకంగా పనిచేస్తుంది.

Students can go through AP Inter 2nd Year Botany Notes 2nd Lesson ఖనిజ పోషణ will help students in revising the entire concepts quickly.

AP Inter 2nd Year Botany Notes 2nd Lesson ఖనిజ పోషణ

→ అన్ని జీవులకు పెరుగుదల, వృద్ధికి కార్టోహైడ్రేట్లు, ప్రొటీన్లు, కొవ్వులు వంటి స్థూల అణువులు, నీరు, వివిధ ఖనిజాలు ఎంతో అవసరము.

→ మొక్కలను నిర్దిష్ట మూలకాల ద్రావణంలో పెంచే సాంకేతిక పద్ధతిని హైడ్రోపోనిక్స్ అంటారు.

→ C, H, O, N, P, K, Ca, Mg మరియు Sలు స్థూల మూలకాలు.

→ Fe, Mn, In, MO, Cu, Cl, B మరియు Ni లు సూక్ష్మ మూలకాలు.

→ C, H, O లను నిర్మాణాత్మక మూలకాలు అంటారు.

→ మొక్కలలో శక్తి సంబంధ రసాయన పదార్థాలలో భాగంగా ఉన్న ఆవశ్యక మూలకాలు Mg, ఫాస్పరస్.

→ నికెల్, యూరియేజ్ అను ఎన్జైమ్కు ఉత్ప్రేరకము. ఇది నత్రజని జీవక్రియలో పాల్గొంటుంది.

→ ఆవశ్యక మూలకం గాఢత తక్కువైనపుడు మొక్క పెరుగుదల ఆగిపోయినట్లయితే ఆ గాఢతను సందిగ్ధ గాఢ అంటారు.

→ నత్రజని, పొటాషియమ్, మెగ్నీషియమ్ లోప లక్షణాలు వృద్ధ పత్రాలలో గోచరిస్తాయి.

→ సల్ఫర్, కాల్షియంల లోప లక్షణాలు మొదట లేత పత్రాలలో కనిపిస్తాయి.

→ పత్రాలు పత్రహరితాన్ని కోల్పోయి, పసుపు వర్ణంలోకి మారుటను నిర్హరితం అంటారు.

→ Ca, Mg, Cu మరియు K లోపం వల్ల కణజాలాలు చనిపోవడం జరుగును.

→ నికెల్ లోపం వల్ల పెకాన్ లో మౌస్ ఇయర్ వ్యాధి కలుగును.

→ అయాన్లు నిష్క్రియా లేక సక్రియా పద్ధతి ద్వారా శోషించబడతాయి.

→ ఖనిజ మూలకాలు బాష్పోత్సేకకర్షణ వల్ల దారువులో ఊర్ధ్వముఖంగా వహనం చెందుతున్న నీటి ద్వారా స్థానాంతరణ చెందుతాయి.

→ మొక్కల పెరుగుదలకు, అభివృద్ధికీ ‘కావలసిన అత్యధిక పోషకాలు శైథిల్యమైన (విచ్ఛిన్నం చెందిన) శిలల నుంచి ఏర్పడిన మృత్తిక ద్వారా వేర్లకు అందించబడతాయి.

→ నత్రజని సజీవులలో అత్యధికంగా ఉన్న మూలకము.

→ నత్రజని క్షయకరణం చెందించే నైట్రోజినేజ్ ఎన్జైమ్ ప్రత్యేకంగా కేంద్రకపూర్వ జీవులలోనే ఉంటుంది. వాటిని N2 స్థాపక జీవులు అంటారు.

→ నైట్రోజినేజ్ ఎన్జైమ్ MO – Fe ప్రొటీను. ఇది వాతావరణ నైట్రోజన్ ను అమ్మోనియాగా మారుస్తుంది.

→ నైట్రోజినేజ్ ఎన్జైమ్లను రక్షించడానికి లెగ్ హీమోగ్లోబిన్ అను ఆక్సిజన్ సమ్మారకం ఉంటుంది.

→ అమైడ్లు (ఆస్పర్జిన్, గ్లూటమిన్) లు మొక్కలలో ఎక్కువగా లభిస్తాయి. ఇవి ఎక్కువగా నత్రజనిని కలిగి ఉంటాయి. కనుక అవి మొక్కల దారునాళాల ద్వారా ఇతర భాగాలకు రవాణా చెందుతాయి).

Students can go through AP Inter 2nd Year Botany Notes 1st Lesson మొక్కలలో రవాణా will help students in revising the entire concepts quickly.

AP Inter 2nd Year Botany Notes 1st Lesson మొక్కలలో రవాణా

→ మొక్కలలో ఒక నిమిషంలో జరిగే పెరుగుదలను ఒక మిల్లీమీటర్ లోని పదిలక్షల వంతును నమోదు చేయగలిగే అంత సూక్ష్మగాహ్యంగా ఉన్న క్రెస్కోగ్రాఫ్ను సర్.జె.సి.బోస్ రూపొందించారు.

→ బోస్ పరిశోధనా సంస్థ కోల్కత్తాలో ఉన్నది.

→ ఎక్కువ దూరాల మధ్య జరిగే రవాణా నాళికావ్యవస్థ ద్వారా జరుగుతుంది. దీనిని స్థానాంతరణ అంటారు. నేలలో నాటుకొని ఉన్న మొక్కలలో దారువు ద్వారా జరిగే రవాణా తప్పనిసరిగా ఒకే దిశలో అనగా వేరు నుంచి కాండంలోకి జరుగుతుంది.

→ సేంద్రియ, ఖనిజ పోషకాలు అన్ని దిశలలో రవాణా చెందుతాయి.

→ వాయువులు లేదా ద్రవాలు అధిక గాఢత గల ప్రదేశం నుండి అల్ప గాఢత గల ప్రదేశంలోనికి చలించుటను అంటారు.

→ త్వచ ప్రొటీన్ల సహాయంతో విసరణ జరగాలంటే అంతకు ముందే గాఢత ప్రవణత ఏర్పడి ఉండాలి. దీనిని సులభతర విసరణ అంటారు.

→ పదార్థాలను గాఢతా ప్రవణతకు వ్యతిరేక దిశలో ప్రవహింపచేయడానికి శక్తిని వినియోగించే విధానమే సక్రియా రవాణా.

→ మొక్క జీవక్రియలన్నింటిలో నీరు ప్రధానంగా పాల్గొంటుంది. అన్ని జీవరాశులకు నీరు ముఖ్యంగా కావలసిన పదార్థం.

→ పూర్తి స్థాయికి పెరిగిన మొక్కజొన్న 1 రోజులో దాదాపు 3 లీటర్ల నీటిని పీల్చుకుంటుంది. కాగా ఆవమొక్క 5 గంటలలో తను బరువుకు సమానమైన నీటిని గ్రహిస్తుంది.

→ నీటిశక్మము = ద్రావిత శక్మము + పీడన శక్మము.

→ స్వచ్ఛమైననీటి నీటిశర్మ విలువ = 0

→ ద్రావిత శక్మం ఎల్లప్పుడూ ఋణాత్మకము.

→ పీడన శక్మం ధనాత్మకం కాని మొక్కలలో ఋణాత్మకము.

→ అర్థ పారగమ్య త్వచం ద్వారా నీరు అల్ప గాఢత గల ప్రదేశం నుంచి అధిక గాఢత గల ప్రదేశంలోకి రవాణా అగుటను ద్రవాభిసరణ అంటారు.

→ ద్రవాభిసరణను థిసిల్ గరాటు ప్రయోగం లేదా పొటాటో ఆస్మాస్కోప్ ప్రయోగము ద్వారా వివరించవచ్చు.

→ కణాల నుంచి నీరు బయటకు వెళ్ళిపోయినప్పుడు కణత్వచం కణ కవచం నుండి విడిపోయి కణద్రవ్య సంకోచం జరుగుతుంది.

→ సాధారణ జీవకణాలు అధిక గాఢత గల ద్రావణంలో ఉంచినప్పుడు శుథం చెందుతాయి. అలాంటి కణాలలో పీడనశక్మం ‘0’ అవుతుంది. కావున నీటిశక్మం, ద్రావితశక్మం సమానం అవుతాయి.

→ కొల్లాయిడ్ల వంటి ఘన పదార్థాలు నీటిని అధిశోషించుకొని విస్తారంగా ఘనపరిమాణంలో వృధ్ధి చెందే ప్రక్రియను నిపానం అంటారు. ఉదా : విత్తనాలు పొడిగా ఉన్న కొమ్మలు నీటిని పీల్చుకునే విధానము.

→ ప్రొటీన్లకు అధిక నివాన సామర్థ్యము, కార్బోహైడ్రేటులకు తక్కువ నిపాన సామర్థ్యం ఉంటాయి. అందువల్ల ప్రొటీన్లు ఎక్కువగా గల బఠాణీ గింజలు, పిండి పదార్థము ఎక్కువగా ఉన్న గోధుమగింజల కంటే ఎక్కువగా ఉబ్బుతాయి.

→ స్థూల ప్రవాహంలో పదార్థాలు రెండు బిందువుల మధ్య ఉన్న పీడన వ్యత్యాసాల వల్ల ఒక చోటు నుంచి మరొక చోటుకు స్థూలంగా చలిస్తాయి.

→ మూలకేశంలోకి ప్రవేశించిన నీరు దిగువన ఉన్న వేరు పొరలకు అపోప్లాస్ట్ పథం లేదా సింప్లాస్ట్ పథం ద్వారా చేరుతుంది.

→ శిలీంధ్రం, వేరు వ్యవస్థతో కలిసి ఏర్పడిన సహజీవన సాంగత్యాన్ని శిలీంధ్ర మూలము (మైకోరైజా) అంటారు.

→ నీరు నీటి బిందువుల రూపంలో బయటకు పోవుటను బిందుస్రావం అంటారు.

→ సిక్వియా సిమ్ పర్విరెన్స్ వంటి చాలా ఎత్తయిన వృక్షాలలో ఎక్కువ భాగము నీటి స్థానాంతరణకు వేరు పీడనం సరిపోదు.

→ సంసంజన – అసంజన, బాష్పోత్సేక కర్షణ నమూనాను డిక్సన్ ప్రతిపాదించారు.

→ పత్ర రంధ్రాలు పగలు తెరుచుకుని, రాత్రి మూసుకుంటే, ఫొటోయాక్టివ్ రకం అంటారు.

→ రసయుత మొక్కలలో (ఉదా : కాక్టస్లు, బయోఫిల్లమ్) పత్రరంధ్రాలు పగలు మూసుకుని రాత్రులందు తెరుచుకుంటాయి. వీటిని స్కోటోయాక్టివ్ రకం అంటారు.

→ పత్రరంధ్రాలు తెరుచుకునే మూసుకునే యాంత్రికాన్ని వివరించడానికి లెవిట్, K’ పంపు సిద్ధాంతాన్ని ప్రతిపాదించారు.

→ A B A (అబ్సిసిక్ ఆమ్లము) అనే సహజ బాష్పోత్సేక నిరోధకము నీటికొరత సందర్భాలలో పత్రరంధ్రం మూసుకునేటట్లు చేస్తుంది.

→ బాష్పోత్సేకం వల్ల మొక్కలకు అనేక ఉపయోగాలు ఉన్నాయి. అందువల్ల దీనిని “అవశ్యకమైన అనర్థం” గా అభివర్ణిస్తారు.

→ పీడన ప్రవాహం లేదా సమూహ ప్రవాహ సిద్ధాంతంను ముంచ్ ప్రతిపాదించారు.

→ సర్. జె.సి. బోస్
జననము : నవంబర్ 30, 1858
మరణము : నవంబర్ 23, 1937
దేశము : ఇండియన్
మొక్కలకు కూడ ప్రాణము ఉంటుందని వాటికి భావవ్యక్తీకరణ ఉంటుందని శాస్త్ర ప్రపంచానికి తెలియచేసిన వ్యక్తి సర్. జగదీష్ చంద్రబోస్. ఆయన సూక్ష్మతరంగ ధైర్ఘ్యవిద్యుత్ అయస్కాంత తరంగాల ను ఉత్పత్తి చేసి రేడియోతరంగాలను గుర్తించే ‘కొహెరర్’ అనుపరికరం రూపకల్పన చేసారు. ఆయన క్రెస్కోగ్రాఫ్ అనే అత్యంత అధునాతన పరి కరాన్ని రూపొందించారు. ఇది మొక్కలలో ఒక నిమిషంలో జరిగే పెరుదల ను ఒక మిల్లిమీటర్లోని పదిలక్షలవంతు వరకు నమోదు చేయకలిగే అంతసూక్ష్మ గ్రాహ్యంగా ఉంటుంది. బ్రిటిష్ ప్రభుత్వం ఆయనను ‘నైట్ హుడ్'(Knight Hood)గా అభివర్ణిస్తూ, అతని పేరుకు ముందు “సర్” అను బిరుదు నిచ్చినది.

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(e) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(e)

అభ్యాసం – 8(ఇ)

క్రింది అవకలన సమీకరణాలను ఏకఘాతీయ సమీకరణ రూపంలో రాసి I.F. లను కనుక్కోండి.

ప్రశ్న 1.
x \(\frac{d x}{d y}\) – y = 2x² sec² 2x
సాధన:
x \(\frac{d x}{d y}\) – y = 2x² sec² 2x
\(\frac{d x}{d y}\) – \(\frac{1}{x} \cdot y\) = 2x. sec² 2x
x లో రేఖీయ సమీకరణము
I.F. = \(\int_e-\frac{1}{x} \log x\) = e^{-log x} = e^{log 1/x} = \(\frac{1}{x}\)

ప్రశ్న 2.
y \(\frac{d x}{d y}\) – x = 2y³
సాధన:
y \(\frac{d x}{d y}\) – x = 2y³
\(\frac{d x}{d y}\) – \(\frac{1}{y} \cdot x\) = 2y²
I.F. = \(e^{\int-\frac{1}{y}} d y\) = e^{-log y} = \(e^{\log \frac{1}{y}}\) = \(\frac{1}{y}\)

II. క్రింది అవకలన సమీకరణాలను సాధించండి.

ప్రశ్న 1.
\(\frac{d y}{d x}\) + y tan x = cos³ x (May ’11)
సాధన:
I.F. = \(e^{\int \tan x d x}\) = e^{log sec x} = sec x
y. sec x = \(\int \sec x \cdot \cos ^3 x d x\)
= \(\int \cos ^2 x d x\)
= \(\frac{1}{2} \int(1+\cos 2 x) d x\)
= \(\frac{1}{2}\left(x+\frac{\sin 2 x}{2}\right)\) + c
సాధన 2y = x cos x + sin x. cos² x + c. cos x

ప్రశ్న 2.
\(\frac{d y}{d x}\) + y sec x = tan x
సాధన:

సాధన
y(sec x + tan x) = sec x + tan x – x + c

ప్రశ్న 3.
\(\frac{d y}{d x}\) – y tan x = e^x sec x.
సాధన:
I.F. = \(e^{-\int \tan x d x}\) = e^{log cos x} = cos x
y. cos x = ∫e^x. sec x. cos x dx = ∫ e^x dx
= e^x + c

ప్రశ్న 4.
x. \(\frac{d y}{d x}\) + 2y = log x.
సాధన:
I.F. = \(e^{\int \frac{2}{x} d x}\) = e^{2 log x} = e^{log x}2 = x²
= ∫x log x dx
= ∫log x. \(\left(\frac{x^2}{2}\right)\) – \(\frac{1}{2} \int x^2 \cdot \frac{1}{x} d x\)
= \(\frac{x^2}{2}\) log x – \(\frac{x^2}{4}\) + c

ప్రశ్న 5.
(1 + x²)\(\frac{\mathbf{d y}}{\mathbf{d x}}\) + y = \(e^{\tan ^{-1} x}\). (May ’07) (A.P. Mar. ’16)
సాధన:
\(\frac{d y}{d x}\) + \(\frac{1}{1+x^2}\).y = \(\frac{e^{\tan ^{-1} x}}{1+x^2}\)

ప్రశ్న 6.
\(\frac{d y}{d x}\) + \(\frac{2 y}{x}\) = 2x²
సాధన:
I.F. = \(e^{\int \frac{2}{x} d x}\) = e^{2 log x} = \(e^{\log x^2}\) = x²
y. x² = ∫2x⁴ dx = \(\frac{2 x^5}{5}\) + c

ప్రశ్న 7.
\(\frac{d y}{d x}\) + \(\frac{4 x}{1+x^2} y\) = \(\frac{1}{\left(1+x^2\right)^2}\)
సాధన:

ప్రశ్న 8.
x\(\frac{d y}{d x}\) + y = (1 + x)e^x
సాధన:

ప్రశ్న 9.
\(\frac{d y}{d x}\) + \(\frac{3 x^2}{1+x^3}\)y = \(\frac{1+x^2}{1+x^3}\)
సాధన:

ప్రశ్న 10.
\(\frac{d y}{d x}\) – y = -2e^-x.
సాధన:
I.F = \(e^{\int-d x}\) = e^-x
y. e^-x = -2∫e^2xdx = e^-2x + c
y = e^-x + c. e^x

ప్రశ్న 11.
(1 + x²)\(\frac{d y}{d x}\) + y = tan^-1x.
సాధన:

ప్రశ్న 12.
\(\frac{d y}{d x}\) + y tan x = sin x. [T.S. Mar. 16]
సాధన:
I.F. e^{∫tan x dx} = e^{log sec x} = sec x
y. sec x = ∫sin x. sec x dx = ∫tan x dx
= log sec x + c

III. ఈ క్రింది అవకలన సమీకరణాలను సాధించండి.

ప్రశ్న 1.
cos x. \(\frac{d y}{d x}\) + y sin x = sec² x
సాధన:
\(\frac{d y}{d x}\) + tan x. y = sec³ x
I.F. = e^{∫tan x dx} = e^{log sec x} = sec x
y. sec x = ∫sec⁴x dx = ∫(1 + tan² x) sec² x dx
= tan x + \(\frac{\tan ^3 x}{3}\) + c

ప్రశ్న 2.
sec x. dy = (y + sin x) dx.
సాధన:

ప్రశ్న 3.
x log x. \(\frac{d y}{d x}\) + y = 2 log x
సాధన:

ప్రశ్న 4.
(x + y + 1)\(\frac{d y}{d x}\) = 1 (Mar. 05)
సాధన:
\(\frac{d x}{d y}\) = x + y + 1
\(\frac{d x}{d y}\) – x = y + 1
I.F. = e^∫-dy = e^-y
x. e^-y = ∫e^-y (y + 1) dy
= -(y + 1). e^-y + ∫e^-y. dy
= -(y + 1) e^-y – e^-y
= -(y + 2) e^-y + c
x = -(y + 2) + c. e^y

ప్రశ్న 5.
x(x – 1)\(\frac{d y}{d x}\) – y = x³(x – 1)³
సాధన:

ప్రశ్న 6.
(x + 2y³)\(\frac{d y}{d x}\) = y
సాధన:

ప్రశ్న 7.
(1 – x²)\(\frac{d y}{d x}\) + 2xy = x\(\sqrt{1-x^2}\)
సాధన:

ప్రశ్న 8.
x(x – 1)\(\frac{d y}{d x}\) – (x – 2)y = x³(2x – 1)
సాధన:
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) – \(\frac{x-2}{x(x-1)} y\) = \(\frac{x^3(2 x-1)}{x(x-1)}\)
I.F. = \(e^{\int \frac{2-x}{x(x-1)}} d x\)
\(\frac{2-x}{x(x-1)}\) = \(\frac{A}{x}\) + \(\frac{B}{x-1}\)
2 – x = A(x – 1) + B.x
x = 0 ⇒ 2 = -A ⇒ A = -2
x = 1 ⇒ 1 – B ⇒ B = 1

ప్రశ్న 9.
\(\frac{d y}{d x}\)(x²y³ + xy) = 1 (Mar. ’11)
సాధన:
\(\frac{d x}{d y}\) =xy + x²y³
ఇది బెర్నౌలీ సమీకరణము
x^-2. \(\frac{d x}{d y}\) – \(\frac{1}{x} \cdot y\) = y³
z = \(-\frac{1}{x}\) అనుకొంటే \(\frac{\mathrm{dz}}{\mathrm{dy}}\) = \(\frac{1}{x^2} \frac{d x}{d y}\)

ప్రశ్న 10.
\(\frac{d y}{d x}\) + x sin 2y = x³ cos² y
సాధన:

ప్రశ్న 11.
y² + (x – \(\frac{1}{y}\))\(\frac{d y}{d x}\) = 0
సాధన:

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(d) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(d)

అభ్యాసం – 8(డి)

I. క్రింది అవకలన సమీకరణములను సాధించండి.

ప్రశ్న 1.
\(\frac{\mathbf{d y}}{\mathbf{d x}}\) = \(-\frac{(12 x+5 y-9)}{5 x+2 y-4}\)
సాధన:
b = -5, a = 5 ⇒ b = -a
(5x + 2y – 4)dy = (12x + 5y – 9) dx
(5x + 2y – 4)dy + (12x + 5y – 9) dx = 0
5 (x dy + y dx) + 2y dy – 4 dy + 12 x dx – 9 dx = 0
సమాకలనముచేయగా 5xy + y² – 4y + 6x² – 9x = c

ప్రశ్న 2.
\(\frac{\mathbf{d y}}{\mathbf{d x}}\) = \(\frac{-3 x-2 y+5}{2 x+3 y+5}\)
సాధన:
b = -2, a = 2 ⇒ b = -a
(2x + 3y + 5) dy = (- 3x – 2y + 5) dx
2x dy + 3y dy + 5 dy = -3x dx – 2y dx + 5 dx
2(x dy + y dx) + 3y dy + 3x dx + 5 dy – 5 dx = 0
సమాకలనము చేయగా
2xy + \(\frac{3}{2} y^2\) + \(\frac{3}{2} x^2\) + 5y – 5x = c
4xy + 3y² + 3x² – 10x + 10y = 2c = c’
సాధన
4xy + 3(x² + y²) – 10(x – y) = c

ప్రశ్న 3.
\(\frac{d y}{d x}\) = \(\frac{-3 x-2 y+5}{2 x+3 y-5}\)
సాధన:
\(\frac{d y}{d x}\) = \(\frac{-(3 x-2 y+5)}{2 x+3 y-5}\)
ఇక్కడ b = -2, a’ = 2
∵ b = -a’
(2x + 3y – 5) dy = -(3x – 2y + 5) dx
⇒2(x dy + y dx) + (3y – 5) dy + (3x – 5) dx = 0
⇒ 2d (xy) + (3y – 5) dy + (3x – 5) dx = 0
ఒక్కొక్కదాన్ని సమాకలనము చేయగా
2 \(\int\)d (xy) + \(\int\) (3y – 5) dy + \(\int\) (3x – 5) dx = 0
⇒2xy + 3.\(\frac{y^2}{2}\) – 5y + 3\(\frac{x^2}{2}\) – 5x = \(\frac{c}{2}\)
(లేదా) 3x² + 4xy + 3y² – 10x – 10y = c
కావలసిన సాధన

ప్రశ్న 4.
2(x – 3y + 1) \(\frac{d y}{d x}\) = 4x – 2y + 1
సాధన:
(2x – 6y + 2) dy = (4x – 2y + 1) dx
(2x – 6y + 2) dy – (4x – 2y + 1) dx = 0
2 (x dy + y dx) – 6y dy + 2 dy – 4x dx – dx = 0
సమాకలనము చేయగా, సాధన
2xy – 3y² – 2x² + 2y – x = c

ప్రశ్న 5.
\(\frac{d y}{d x}\) = \(\frac{x-y+2}{x+y-1}\)
సాధన:
b = -1, a’ – 1 ⇒ b = – a’
(x + y – 1) dy = (x – y + 2) dx
(x + y – 1) dy = (x − y + 2) dx = 0
(x dy + y dx) + y dy – dy – x dx – 2 dx = 0
సమాకలనము చేయగా
xy + \(\frac{y^2}{2}\) – \(\frac{x^2}{2}\) – y – 2x = c
2xy + y² – x² – 2y – 4x = 2c = c’

ప్రశ్న 6.
\(\frac{d y}{d x}\) = \(\frac{2 x-y+1}{x+2 y-3}\)
సాధన:
b = -1, a’ = 1 ⇒ b = -a’
(x + 2y – 3) dy = (2x – y + 1) dx
(x + 2y – 3) dy – (2x – y + 1) dx = 0
(x dy + y dx) + 2y dy – 3 dy – 2x dx – dx = 0
సమాకలనము చేయగా
xy + y² – x² – 3y – x = c

II. కింది అవకలన సమీకరణాలను సాధించండి.

ప్రశ్న 1.
(2x + 2y + 3) \(\frac{d y}{d x}\) = x + y + 1
సాధన:

9 తో గుణించగా
6v + log (3v + 4) = 9x + 9c
6(x + y) + log[3(x + y) + 4] = 9x + c
i.e. log (3x + 3y + 4) = 6y – 3x + c

ప్రశ్న 2.
\(\frac{d \mathbf{y}}{\mathbf{d x}}\) = \(\frac{4 x+6 y+5}{3 y+2 x+4}\)
సాధన:
\(\frac{d \mathbf{y}}{\mathbf{d x}}\) = \(\frac{4 x+6 y+5}{2 x+3 y+4}\)
v = 2x + 3y

64 తో గుణించగా
8v + 9 log (8v + 23) = 64x + 64c
8 (2x + 3y) – 64x + 9 log (16x + 24y + 23) = c’
8 తో భాగించగా
2x + 3y – 8x + \(\frac{9}{8}\) log (16x + 24y+23) = c”
3y – 6x + \(\frac{9}{8}\) log (16x + 24y + 23) = c”
3 తో భాగించగా సాధన
y – 2x + \(\frac{3}{8}\) log (16x + 24y + 23) = k

ప్రశ్న 3.
(2x + y + 1) dx + (4x + 2y – 1) dy = 0
సాధన:

2v + log (v – 1) = 3x + c
2v – 3x + log (v – 1) = c
2(2x + y) – 3x + log (2x + y – 1) = c
4x+2y-3x + log (2x + y – 1) = c
సాధన x + 2y + log (2x + y – 1) = c

ప్రశ్న 4.
\(\frac{d y}{d x}\) = \(\frac{2 y+x+1}{2 x+4 y+3}\)
సాధన:

8 తో గుణించగా
4v + log (4v + 5) = 8x + 8c
4(x + 2y) – 8x + log [4(x + 2y) + 5] = c’
సాధన
4x + 8y – 8x + log (4x + 8y + 5) = c’
8y – 4x + log (4x + 8y + 5) = c’

ప్రశ్న 5.
(x + y – 1) dy = (x + y + 1) dx
సాధన:

v – log v = 2x + c
x + y – log (x + y) = 2x – c
(x – y) + log (x + y) = c అనేది కావలసిన సాధన

III. కింది అవకలన సమీకరణాలను సాధించండి.

ప్రశ్న 1.
\(\frac{d y}{d x}\) = \(\frac{3 y-7 x+7}{3 x-7 y-3}\) (T.S. Mar. ’16)
సాధన:
x = x + h, y = y + k అనుకుంటే \(\frac{d y}{d x}\) = \(\frac{d y}{d x}\)


⇒ 14 ln x – ln c
= 3ln (v – 1) – 3ln (v + 1) – 7ln (v + 1) – 7ln (v – 1).
14ln x – ln c = 10 ln (v + 1) – 4 ln (v – 1)
ln (v + 1)⁵ + ln (v – 1)² + ln x⁷ = ln c
(v + 1)⁵. (v – 1)². x⁷ = c
\(\left(\frac{y}{x}+1\right)^5\left(\frac{y}{x}-1\right)^2\) . x⁷ = c
(y – x)² (y + x)⁵ = c
[y – (x – 1)]² (y + x – 1)⁵ = c
సాధన [y – x + 1]² (y + x – 1)⁵ = c.

ప్రశ్న 2.
\(\frac{\mathbf{d y}}{\mathbf{d x}}\) = \(\frac{6 x+5 y-7}{2 x+18 y-14}\)
సాధన:
\(\frac{\mathbf{d y}}{\mathbf{d x}}\) = \(\frac{6 x+5 y-7}{2 x+18 y-14}\)
x = X + h, y = Y + k


14 = A – \(\frac{7}{3}\) ⇒ A = 6
V = \(-\frac{1}{2}\) ⇒ 2 – 9 = B\(\left(-\frac{3}{2}-2\right)\)
-7 = \(-\frac{7}{2} B\) ⇒ B = 2
\(\int\left(\frac{6}{3 V-2}+\frac{2}{2 V+1}\right) d V\) = \(-3 \int \frac{d x}{x}\)
2 log(3V – 2) + log (2V + 1) = -3 log X + log c
log (3V – 2)².(2V + 1) + log X³ = log c
log X³(3V – 2) (2V + 1) = log c
X³(3v – 2)² (2V + 1) = c

ప్రశ్న 3.
\(\frac{d y}{d x}\) + \(\frac{10 x+8 y-12}{7 x+5 y-9}\) = 0
సాధన:

h, k విలువలను 10h + 8k – 12 = 0
7h + 5k – 9 = 0 అయ్యే విధంగా ఎన్నుకొందాం


5V + 7 = A(V + 2) + B (V + 1)
V = -1 ⇒ 2 = A(-1 + 2) = A ⇒ A = 2
V = -2 = -3 = B(-2 + 1) = -B, B = 3
\(\int\left(\frac{2}{(V+1)}+\frac{3}{(V+2)}\right) d V\) = \(-5 \int \frac{d X}{X}\)
2 log(V + 1) + 3 log (V + 2) = -5 log x + c
c = 2log(V + 1) + 3 log(V + 2) + 5 log X
= log (V + 1)². (V + 2)³. X⁵
log \(\left(\frac{Y}{X}+1\right)^2\) . \(\left(\frac{Y}{X}+2\right)^3\). X⁵
= log \(\frac{(Y+X)^2}{X^2} \frac{(Y+2 X)^3}{X^3}\) . X⁵
⇒ (Y + X)² . (Y + 2X)³ = e^c = c¹
(Y + 1 – X – 2)² (Y + 1 – 2x – 4)³ = c
సాధన: (x + y – 1)² (2x + y – 3)³ = c.

ప్రశ్న 4.
(x – y – 2) dx + (x – 2y – 3) dy = 0
సాధన:
దత్త సమీకరణము \(\frac{d y}{d x}\) = \(\frac{-x+y+2}{x-2 y-3}\)
x = X + h, y = Y + k
\(\frac{d y}{d x}\) = \(\frac{-(X+h)+(Y+k)+2}{(X+h)-2(Y+k)-3}\)
= \(\frac{-X-h+(-h+2 k+2)}{(X-2 Y)+(h-2 k-3)}\)
h, k విలువలు – h + k − 2 = 0
h – 2k – 3 = 0 అయ్యేవిధంగా ఎన్నుకొందాం.




కావలసిన సాధన

ప్రశ్న 5.
(x – y) dy = (x + y + 1) dx
సాధన:
\(\frac{d y}{d x}\) = \(\frac{x+y+1}{x-y}\)
x = X +h, y = Y + k ⇒ \(\frac{d Y}{d X}\) = \(\frac{\mathrm{dy}}{\mathrm{dx}}\)
\(\frac{d y}{d x}\) = \(\frac{X+h+Y+k+1}{(X+h)-(Y+k)}\)
= \(\frac{(X+Y)+(h+k+1)}{(X-Y)+(h-k)}\)
h, k విలువ లను h + k + 1 = 0
h – k = 0 అయ్యే విధంగా ఎన్నుకొందాం
సాధించగా h = \(-\frac{1}{2}\), k = \(-\frac{1}{2}\)
∴ \(\frac{d y}{d X}\) = \(\frac{X+Y}{X-Y}\)

tan^-1 V – \(\frac{1}{2}\)log (1 + v²) = log x + log c
2 tan^-1 V = log (1 + V²) + 2 log x + 2 log c = log c²x² (1 + v²)

ప్రశ్న 6.
(2x + 3y – 8) dx = (x + y – 3) dy
సాధన:
\(\frac{d y}{d x}\) = \(\frac{2 x+3 y-8}{x+y-3}\)
x = X + h, y = Y + k ⇒ \(\frac{\mathrm{d} Y}{\mathrm{~d} X}\) = \(\frac{\mathrm{dy}}{\mathrm{dx}}\)
\(\frac{d Y}{d X}\) = \(\frac{2(X+h)+3(Y+k)-8}{(X+h)+(Y+k)-3}\)
= \(\frac{(2 X+3 Y)+(2 h+3 k-8)}{(X+Y)+(h+k-3)}\)
h, k విలువ లను 2h + 3k – 8 = 0
h + k – 3 = 0 అయ్యే విధంగా ఎన్నుకొందాం


(1 + V) = A(2 – 2V) + B అనుకొందాం
V గుణకాలు సమానం చేయగా
1 = – 2A ⇒ A = -1/2
స్థిర పదాలు సమానం చేయగా
1 = 2A + B
= -1 + B
B = 2


ఇక్కడ, X = x – 1, Y = y – 2

ప్రశ్న 7.
\(\frac{d y}{d x}\) = \(\frac{x+2 y+3}{2 x+3 y+4}\)
సాధన:
x = X + h, y = Y + k అయితే \(\frac{d \mathrm{Y}}{\mathrm{dX}}\) = \(\frac{d y}{d x}\)
\(\frac{d Y}{d X}\) = \(\frac{(X+h)+2(Y+k)+3}{2(X+h)+3(Y+k)+4}\)
= \(\frac{(X+2 Y)+(h+2 k+3)}{(2 X+3 Y)+(2 h+3 k+4)}\)
h, k విలువలకు h + 2k + 3 = 0
2h + 3k + 4 = 0 అయ్యే విధంగా ఎన్నుకొందాం.

\(\frac{\mathrm{d} Y}{\mathrm{dX}}\) = \(\frac{X+2 Y}{2 X+3 Y}\)
ఇది సమఘాత సమీకరణము

ప్రశ్న 8.
\(\frac{d y}{d x}\) = \(\frac{2 x+9 y-20}{6 x+2 y-10}\)
సాధన:
దత్త సమీకరణము \(\frac{d y}{d x}\) = \(\frac{2 x+9 y-20}{6 x+2 y-10}\)
x = X + h, y = Y + k ⇒ \(\frac{d Y}{d X}\) = \(\frac{d y}{d x}\)
\(\frac{\mathrm{dY}}{\mathrm{dX}}\) = \(\frac{2(X+h)+9(Y+k)-20}{6(X+h)+2(Y+k)-10}\)
= \(\frac{(2 X+9 Y)+(2 h+9 k-20)}{(6 X+2 Y)+(6 h+2 k-10)}\)
h, k విలువలను 2h + 6k – 20 = 0
6h + 2k – 10 = 0 అయ్యే విధంగా ఎన్నుకొందాం

ఇది సమఘాత సమీకరణము
y = VX ⇒ \(\frac{d Y}{d X}\) = V + X. \(\frac{d V}{d X}\)


సాధన (X + 2Y) = (Y – 2X)²
ఇక్కడ X = x – 1, Y = y – 2
c(x – 1 + 2y – 4) = (y – 2 – 2x + 2)²
c(x + 2y – 5) = (y – 2x)²
= (2x – y)²