AP State Board Notes

Students can go through AP Board 7th Class Social Notes 3rd Lesson పటాల ద్వారా అధ్యయనం to understand and remember the concept easily.

AP Board 7th Class Social Notes 3rd Lesson పటాల ద్వారా అధ్యయనం

→ పటాలు మన ప్రయాణాన్ని సులభతరం చేయడంతోపాటు గమ్యాన్ని చేరడంలో కచ్చితత్వాన్ని చూపుతూ మార్గనిర్దేశనం చేస్తాయి.

→ క్రీ.శ. 1498 లో వాస్కోడిగామా భారతదేశంలోని కాలికట్ చేరుకున్నాడు.

→ సముద్ర మార్గం ద్వారా ప్రపంచాన్ని చుట్టి వచ్చిన మొదటి వ్యక్తి మాజిలాన్.

→ పటాల తయారీలో నావికులు, ప్రయాణికుల సహకారం ఎంతో విలువైంది.

→ సుమేరియన్లు బాబిలోనియన్లు ‘మట్టి పలకలను’ పటాలుగా ఉపయోగించారు.

→ అక్షాంశ, రేఖాంశ భావనలను ‘గ్రీకులు’ పటాల తయారీకి అన్వయించారు.

→ పటాల తయారీలో టాలమీ కృషి విశేషమైనదే కాక విరివిగా ఉపయోగించబడింది.

→ గెరార్డస్ మెర్కేటర్ ప్రవేశపెట్టిన ప్రక్షేపణం పటాల తయారీలో విశేష మార్పులను తీసుకు వచ్చింది.

→ పటంలోని అంశాలను లేదా విషయాన్ని పట శీర్షిక తెలుపుతుంది.

→ భూ ఉపరితలంపై వాస్తవ దూరాన్ని పటంలో సవరించి చూపడాన్ని ‘స్కేలు’ తెలియజేస్తుంది.

→ స్కేలును మూడు రకాలుగా చూపవచ్చు. 1) వాక్య రూప స్కేలు, 2) గ్రాఫ్ రూపంలోని స్కేలు, 3) నైష్పత్తిక స్కేలు.

→ వాస్తవ అంశాలను పటంలో యథాతథంగా చూపించడం కష్టం కనుక పటాల తయారీదారులు చిహ్నాలను ఉపయోగిస్తారు.

→ భారత సర్వేక్షణ శాఖ (సర్వే ఆఫ్ ఇండియా) టోపోషీట్స్ తయారీలో సాంప్రదాయక చిహ్నాలు ఉపయోగిస్తుంది.

→ MSL-సముద్రమట్టం నుండి ఎత్తు. ఒక ప్రదేశం యొక్క ఎత్తును కొలవడంలో దీనిని ప్రామాణికంగా స్వీకరిస్తారు.

→ పటములోని వివరాలను చదవడానికి లేదా అర్థం చేసుకోవడానికి ఉపకరించే అంశాలు లేదా చిహ్నాలను కలిగి ఉండే పట్టికను ‘లెజెండ్’ అంటారు.

→ ఒక ప్రదేశం యొక్క ఉనికిని గుర్తించుటకు అక్షాంశ రేఖాంశాలు ప్రాథమిక సమాచారాన్ని ఇస్తాయి.

→ పటాలను స్కేలు, అంశాలు మరియు విషయాల ఆధారంగా రాజకీయ, భౌతిక, విషయ నిర్దేశిత మరియు చారిత్రక పటాలుగా వర్గీకరించవచ్చును.

→ ఒక ప్రదేశం యొక్క పాలనా పరిధిని, పొరుగు దేశాలను, సరిహద్దులను, రాజధానులను, రాజకీయ పటాలు తెలియజేస్తాయి.

→ భారతదేశం 3.28 మి.చ.కి.మీ. విస్తీర్ణంతో ప్రపంచంలో ఏడవ పెద్ద దేశంగా గుర్తించబడింది.

→ మన దేశంలో 28 రాష్ట్రాలు, 8 కేంద్ర పాలిత ప్రాంతాలు కలవు.

→ భారతదేశం ఆసియా ఖండపు దక్షిణ భాగంలో ఉంది. అక్షాంశ రీత్యా 894-37°6′ ఉత్తర అక్షాంశాల మధ్య మరియు 6877-97°25′ తూర్పు రేఖాంశాల మధ్య విస్తరించి ఉంది.

→ కర్కటరేఖ భారతదేశం మధ్య గుండా పోతుంది.

→ అక్షాంశ రేఖాంశాలతో ఏర్పడిన గడుల వంటి అమరికను ‘గ్రిడ్’ అంటారు.

→ పర్వత శ్రేణులు, పీఠభూములు, మైదానాలు, నదులు, ఎడారులు, సరస్సులు, మెట్టభూములు మొదలైన భౌతిక స్వరూపాలకు సంబంధించిన సమాచారాలను తెలిపే పటాలను భౌతిక పటాలు అంటారు.

→ సమాన ఎత్తులో ఉన్న ప్రదేశాలను కలుపుతూ గీసే ఊహారేఖలను కాంటూరు రేఖలు అంటారు.

→ ఏదేని ప్రత్యేక అంశము లేదా విషయాలను తెలుపుటకు తయారు చేయబడిన పటాలను విషయ నిర్దేశిత పటాలు అంటారు.

→ టోపోగ్రాఫిక్ పటాలు భూ ఉన్నతి, భౌతిక స్వరూపము, వ్యవసాయ భూములు, నేలలు, నదులు, జనావాసాలు మొదలైన వివరాలు చూపుతాయి.

→ గడచిపోయిన కాలం యొక్క వివరాలను చూపించే పటాలను ‘చారిత్రక’ పటాలు అంటారు.

→ అశోకుని శాసనాలు : బృహత్ శాసనాలు, స్తంభ శాసనాలు, చిన్న శిలా శాసనాలు.

→ గోళాకారంగా ఉన్న భూమిపై ఉన్న అంశాలైన ఖండాలు ప్రదేశాలను వాటి ఆకారం, దిశలను సమతల ఉపరితలంపై సవరించి చూపడాన్ని ప్రక్షేపణం’ అంటారు.

→ పటాల తయారీలో ప్రక్షేపణ పద్ధతిని ప్రవేశపెట్టినవారు ‘డచ్’ కార్టోగ్రాఫర్ ‘గెరార్డస్ మెర్కేటర్’.

→ రెండు కాంటూరు రేఖల ధ్య గల దూరం, ఎత్తుల మధ్య వ్యత్యాసాన్ని తెలుపుతుంది.

→ కాంటూరు రేఖలు దగ్గరగా ఉంటే ఆ ప్రదేశం యొక్క వాలు తక్కువగా ఉంటుంది. రేఖల మధ్య దూరం ఎక్కువగా ఉంటే ఆ ప్రాంతం యొక్క వాలు ఎక్కువగా ఉంటుంది.

→ రాజకీయ పటాలు : ఒక ప్రదేశం యొక్క పాలనా పరిధిని, పొరుగు దేశాలను, సరిహద్దులను, రాజధానులను తెలియజేసే పటాలు.

→ భౌతిక పటాలు : వివిధ భూస్వరూపాలను, నిర్దిష్ట రంగులు, ఎత్తు పల్లములతో సూచించే పటాలు భౌతిక పటాలు.

→ చారిత్రక పటాలు : గడచిపోయిన కాలం యొక్క వివరాలను చూపించే పటాలను చారిత్రక పటాలు అంటారు. ఉదా : అశోకుని శాసనాలు గల ప్రదేశాలు.

→ శీర్షిక : పటంలోని అంశాలను లేదా విషయాన్ని పట శీర్షిక తెలుపుతుంది.

→ దిక్కులు : సాధారణంగా ఉత్తర దిక్కుకు పైన ఉండే విధంగా పటాలు తయారుచేయ బడతాయి. ప్రధాన దిక్కులు 4 (ఉత్తర, దక్షిణ, తూర్పు, పడమరలు).

→ స్కేలు : భూమిపై కల వాస్తవ దూరానికి పటంలో చూపబడిన దూరానికి కల నిష్పత్తిని స్కేలు అని పిలుస్తాం.

→ స్కేలు రకాలు :

1. వాక్య రూప స్కేలు
2. గ్రాఫ్ రూప స్కేలు
3. నైష్పత్తిక స్కేలు.

→ సాంప్రదాయిక చిహ్నాలు : పటాల తయారీలో ఉపయోగించే కొన్ని గుర్తులు. (వీటిని సర్వే ఆఫ్ ఇండియా టోపోషీట్స్ తయారీలో ఉపయోగిస్తుంది).

→ నమూనా చిత్రాలు : గణాంక వివరాలను, సమాచారాన్ని, పరిమాణాత్మక, గుణాత్మక విశ్లేషణలుగా చూపడానికి వీటిని ఉపయోగిస్తారు.

→ లెజెండ్ : పటములోని వివరాలను చదవడానికి లేదా అర్థం చేసుకోవడానికి ఉపకరించే అంశాలు లేదా చిహ్నాలను కలిగి ఉండే పట్టిక.

→ అక్షాంశ, రేఖాంశాలు : ఒక ప్రదేశం యొక్క ఉనికిని గుర్తించుటకు సంబంధించిన ప్రాథమిక సమాచారాన్ని తెలియజేస్తాయి.

→ అట్లాస్ : పటాల సంకలనాన్ని అట్లాస్ అంటారు.

→ పటాల్లో రకాలు :

1. రాజకీయ పటాలు
2. భౌతిక పటాలు
3. విషయ నిర్దేశిత పటాలు
4. చారిత్రక పటాలు

→ విషయ నిర్దేశిత పటాలు : ఏదేని ప్రత్యేక లేదా నిర్దిష్ట అంశము లేదా విషయాలను తెలుపుటకు తయారుచేయబడిన పటాలు. ఉదా : అడవులను చూపే పటాలు.

→ గ్రిడ్ : అక్షాంశ, రేఖాంశాలతో ఏర్పడిన గడుల వంటి అమరికను గ్రిడ్ అంటారు.

→ కాంటూరు రేఖలు : సమాన ఎత్తులో ఉన్న ప్రదేశాలను కలుపుతూ గీసే ఊహా రేఖలను కాంటూరు రేఖలు అంటారు.

→ ప్రక్షేపణం : గోళాకారంగా ఉన్న భూమిపై ఉన్న అంశాలైన ఖండాలు, ప్రదేశాలను వాటి ఆకారం, దిశలను సమతల ఉపరితలంపై సవరించి చూపడాన్ని ప్రక్షేపణం అంటారు. గెరార్డస్ మెర్కేటర్ ఈ పద్ధతిని ప్రవేశపెట్టాడు.

→ ఉనికి : అట్లాసుపై ఒక ప్రదేశం యొక్క అక్షాంశ, రేఖాంశాలను తెలుపును.

→ టోపోగ్రఫి : ఒక ప్రదేశంనకు సంబంధించిన భౌతిక స్వరూపాలను తెలుపునది.

→ సముద్ర మట్టం నుండి ఎత్తు (MSL) : ఒక ప్రదేశం యొక్క ఎత్తును కొలవడంలో MSL (సముద్ర మట్టం నుండి ఎత్తు)ను ప్రామాణికంగా స్వీకరిస్తారు.

→ ప్రాదేశిక సమాచారం : ఒక ప్రదేశానికి సంబంధించిన ప్రత్యక్ష, పరోక్ష సమాచారం.

→ కార్టోగ్రాఫర్ : పటాలను తయారు చేసేవారిని కార్టోగ్రాఫర్స్ అంటారు.

→ శాసనాలు : అధికారంలో ఉన్న వ్యక్తి లేదా రాజ కుటుంబాలు చేసే అధికారిక ప్రకటన.

→ టోపో షీట్స్ : ఒక ప్రాంతానికి సంబంధించిన సహజ స్వరూపాలు, మానవ సంబంధిత అంశాల వివరాలతో కూడిన పటాలు.

→ కేంద్రపాలిత ప్రాంతాలు : కేంద్ర ప్రభుత్వ పరిధిలోని ఒక పరిపాలన విభాగం.

→ సాంప్రదాయ చిహ్నాలు : భూమిపై వాస్తవ అంశాలను పటంలో చూపే చిహ్నాలు. పటంలో వీటిని వివిధ స్వరూపాలకు, అంశాలకు ప్రత్యామ్నాయంగా ఉపయోగిస్తారు.

→ సముద్రయానం : కొత్త ప్రదేశాల అన్వేషణకు సముద్ర ప్రయాణం చేయటం.

→ నీటి పారుదల : వివిధ వనరుల నుండి నీటి ప్రవాహాలు (ప్రత్యేకించి నదీ ఆధారిత ప్రవాహాలు).

1.

2.

3.

4.

Students can go through AP Board 7th Class Social Notes 2nd Lesson అడవులు to understand and remember the concept easily.

AP Board 7th Class Social Notes 2nd Lesson అడవులు

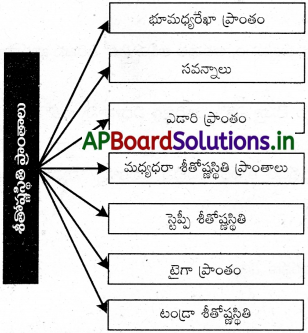
→ ఉష్ణోగ్రత, అవపాతం ఆధారముగా భూగోళ శాస్త్రవేత్తలు శీతోష్ణస్థితి మండలాలను నిర్వచించారు. వీరి ప్రకారం ప్రపంచంలో ఏడు శీతోష్ణ మండలాలు కలవు.

→ భూమధ్య రేఖకు ఇరువైపులా 5–10° ఉత్తర, దక్షిణ అక్షాంశాల మధ్య భూమధ్య రేఖ లేదా ఉష్ణ మండల శీతోష్ణస్థితి ప్రాంతం కలదు.

→ దట్టమైన అడవులతో ఉన్న ఈ (భూమధ్య రేఖ శీతోష్ణస్థితిని) ప్రాంతాన్ని సెల్వాలు అంటారు.

→ అమెజాన్లోని రెడ్ ఇండియన్లు, కాంగో పరీవాహకంలోని పిగ్మీలు వంటి ఆటవిక సమూహాలు ఈ ప్రాంతములో నివసిస్తున్నారు.

→ ‘సవన్నాలు’ భూమధ్యరేఖకు ఇరువైపులా 10°-20° ఉత్తర, దక్షిణ అక్షాంశాల మధ్య విస్తరించి ఉన్నాయి.

→ ‘ఎడారి ప్రాంతాలు’ ఖండాలకు పశ్చిమవైపున 15°-30° ఉత్తర, దక్షిణ అక్షాంశాల మధ్య విస్తరించి ఉన్నాయి.

→ ‘సహారా’ ఎడారి ప్రపంచంలోనే పెద్ద ఎడారి.

→ వేసవిలో పొడి వాతావరణము, శీతాకాలములో ఒక మాదిరి నుండి అధిక వర్షపాతం మధ్యధరా శీతోష్ణస్థితి ప్రాంతం యొక్క ప్రధాన లక్షణము.

→ అర్ధశుష్క ప్రాంతం (సమశీతోష్ణ) లో గడ్డిభూములు ‘స్టెప్పీలు’.

→ టైగా ప్రాంతం ఉత్తరార్ధ గోళంలో 559-70° ఉత్తర అక్షాంశాల మధ్య విస్తరించి ఉంది.

→ టైగా ప్రాంతం ప్రపంచంలో అధిక వాతావరణ వ్యత్యాసాలు కలిగి ఉన్న ప్రాంతాల్లో ఇది ఒకటి.

→ టైగా ప్రాంతంలో ‘ఫర్’ వాణిజ్యము ముఖ్యమైన మరియు ఆకర్షణీయమైన – కార్యకలాపము.

→ ఆర్కిటిక్ – ధృవ ప్రాంతాల మధ్య విస్తరించిన ‘టండ్రా’ ప్రాంతములో చలి చాలా ఎక్కువ.

→ ఒక ప్రదేశం యొక్క ఉష్ణోగ్రత, వర్షపాతం, నేలలు ఆ ప్రాంతం యొక్క వృక్షజాల రకాలను నిర్ధారిస్తాయి.

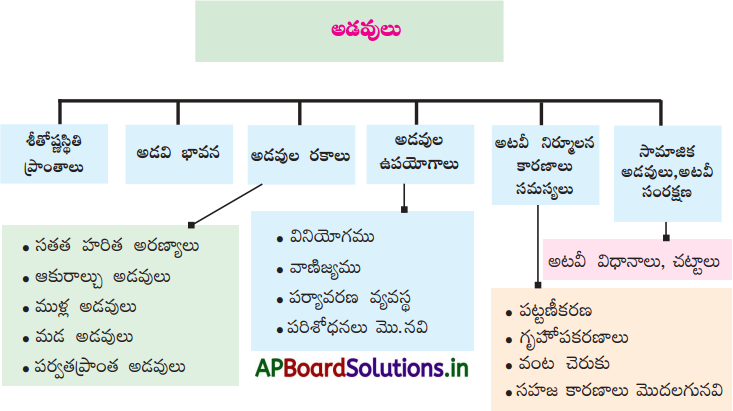
→ విశాల ప్రాంతంలో సహజ పరిస్థితులలో చెట్లు, పొదలతో కూడిన నిర్దిష్ట ప్రాంతాన్ని ‘అడవి’ అని పిలుస్తారు.

→ ఆదిమ జాతుల మనుగడకు అడవులు ప్రధాన స్థావరాలు.

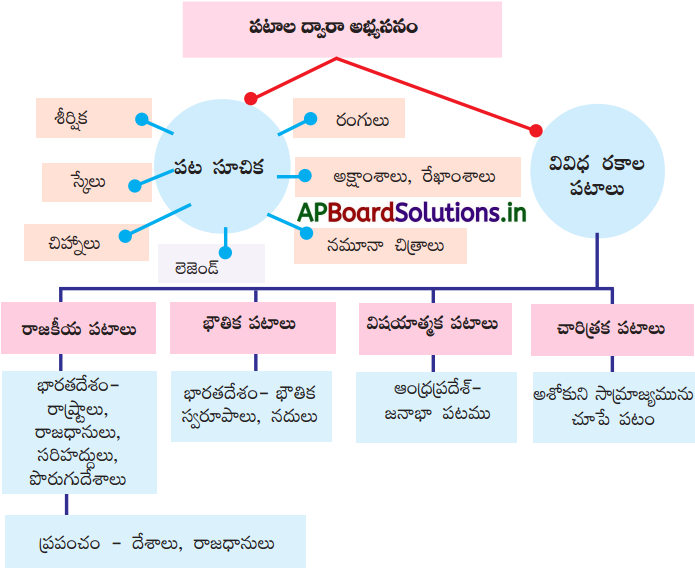
→ భారత ప్రభుత్వము పరిపాలన సౌలభ్యం కొరకు అడవులను మూడు రకాలుగా విభజించింది. అవి రిజర్వు, రక్షిత, వర్గీకరించని అడవులు.

→ వేట, మేత వంటి కార్యకలాపాలను నేషిధించిన అడవులు రిజర్వు అడవులు.

→ ప్రత్యేక వృక్షజాలం, జంతు జాలాలను రక్షించటానికి ఏర్పాటు చేయబడ్డ అడవులు, రక్షిత అడవులు. వర్గీకరించని అడవులలో జీవనోపాధి కొరకు అవసరమైన అటవీ ఉత్పత్తులను సేకరించవచ్చు మరియు పశువులను మేపుకోవచ్చును.

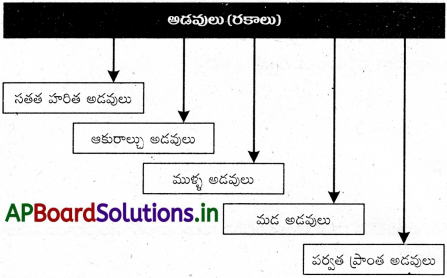
→ అధిక సాంవత్సరిక ఉష్ణోగ్రత మరియు వర్షపాతం ఉన్న ప్రాంతాల్లో ‘సతతహరిత అరణ్యాలు’ పెరుగుతాయి.

→ ఈ అడవులు ఏడాది పొడవునా పచ్చగా ఉంటాయి.

→ హిమాలయ ప్రాంతాలు, ఈశాన్య రాష్ట్రాలు, పశ్చిమ కనుమలు, కేరళలోను ఈ అడవులు పెరుగుతాయి.

→ మహాగని, ఎబోని, రోజ్ వుడ్, ఐవరివుడ్ వంటి వృక్ష జాతులు ఈ అడవులలో పెరుగుతాయి.

→ వివిధ రకాల సరీసృపాలు, సింహపు తోక కోతి (లయన్ టెయిల్డ్ మకాక్), కీటకాలు ఈ అడవుల్లో ఉంటాయి.

→ ఆకురాల్చు అడవులు 70-200 సెం.మీ.. వర్షపాతము ఉన్న ప్రాంతాలలో విస్తరించి ఉన్నాయి.

→ ఆకురాల్చు అడవులు ద్వీపకల్ప పీఠభూమిలో ఎక్కువగా విస్తరించి ఉన్నాయి.

→ ఆకురాల్చు అడవుల్లో టేకు, సాల్, వెదురు, రోజ్ వుడ్, చందనం, వేప వృక్షాలు కనిపిస్తాయి.

→ ఆకురాల్చు అడవుల్లో పులులు, చిరుతలు, కుందేళ్ళు, జింకలు, నెమళ్ళు, పక్షులు ప్రధాన జంతుజాలం.

→ ఆకురాల్చు అడవుల్లోని వృక్షాలు వేసవి నెలల్లో బాష్పోత్సేకాన్ని తగ్గించడానికి ఆకులు రాల్చుతాయి.

→ ముళ్ళ/పొద అడవులు తక్కువ వర్షపాతం వుండి, అధిక ఉష్ణోగ్రత ఉన్న ప్రాంతాల్లో పెరుగుతాయి.

→ ముళ్ళపొద అడవుల్లోని చెట్లు ముళ్లతోనూ, పొదలుగానూ ఉంటాయి.

→ ముళ్ళపొద అడవులు దక్కన్ పీఠభూమి, భారతదేశ ఎడారి ప్రాంతాల్లో ఉన్నాయి.

→ ముళ్ళ/పొద అడవుల్లో అకేషియా, బ్రహ్మ జెముడు, నాగజెముడు, బబుల్ మరియు రేగు వృక్ష జాతులు కలవు.

→ మడ/తీర ప్రాంతపు అడవులను చిత్తడి అడవులు అని కూడా అంటారు.

→ మడ/తీర ప్రాంతపు అడవుల్లోని చెట్లు సముద్రపు లవణీయతను, అలల తాకిడిని తట్టుకునేలా ఉంటాయి.

→ మడ/తీర ప్రాంతపు అడవుల్లో తెల్లమడ, సుందరి, పొన్న, బొడ్డుపొన్న మొదలగు వృక్షాలు పెరుగుతాయి.

→ మడ/తీర ప్రాంతపు అడవుల సమీపంలో చేపలు విరివిగా దొరుకుతాయి.

→ పశ్చిమ బెంగాల్ లోని సుందర్బన్ ప్రాంతాలలో ఈ మడ అడవులు విస్తరించి ఉన్నాయి.

→ పర్వత ప్రాంత అడవులు పర్వతాలు మరియు కొండ ప్రాంతాలలో పెరుగుతాయి.

→ పర్వత ప్రాంత అడవుల్లోని వృక్షాల ఆకులు సన్నని సూది ఆకారంలోనూ, త్రిభుజాకారంలోనూ ఉంటాయి.

→ హిమాలయ ప్రాంతంలో వివిధ రకాలైన శృంగాకారపు అడవులు ఉన్నాయి.

→ స్పర్, ఫర్, విల్లో, దేవదారు, సిల్వర్ ఫర్ మొదలైన వృక్షాలు ఈ అడవుల్లో ఉన్నాయి.

→ ధృవపు జింక, మంచు చిరుత ఇక్కడ ప్రధాన జంతు జాలము.

→ ISFR – ఇండియన్ స్టేట్ ఫారెస్ట్ రిపోర్టు.

→ ISFR – 2019 ప్రకారం భారతదేశములో 8,07,276 చ.కి.మీ. విస్తీర్ణం మేర భూమి అటవీ ప్రాంతములో కప్పబడి ఉంది.

→ మొత్తము భూభాగములో 24.56% ప్రపంచ అటవీ విస్తీర్ణంలో భారతదేశం 10వ స్థానంలో ఉంది.

→ జాతీయ అటవీ విధానం 1952 ప్రకారం మొత్తం భూభాగంలో 33%, మైదాన ప్రాంతాలలో 20%, కొండ ప్రాంతాలలో 60% విస్తీర్ణం గల భూమి అడవుల క్రింద ఉండాలి.

→ విస్తీర్ణ పరంగా మధ్యప్రదేశ్ రాష్ట్రం అత్యధిక అటవీ ప్రాంతాన్ని కల్గి ఉండగా అరుణాచల్ ప్రదేశ్ రెండవ స్థానంలో, హర్యానా చివరి స్థానంలోను ఉన్నాయి.

→ భారతదేశం 3.28 మిలియన్ చ.కి.మీ. విస్తీర్ణం, 30 డిగ్రీల అక్షాంశాల విస్తృతి కల్గి ఉంది.

→ భారతదేశం ఉత్తరం నుంచి దక్షిణానికి మధ్య దూరం 3,214 కి.మీ.లు.

→ భారత జాతీయ అటవీ నివేదిక-2019 ప్రకారం ఆంధ్రప్రదేశ్ రాష్ట్రం 37,392 చ.కి.మీ. విస్తీర్ణం అనగా మొత్తం విస్తీర్ణంలో 22.94% అటవీ ప్రాంతాన్ని కల్గి ఉంది.

→ YSR కడప జిల్లా అత్యధిక అటవీ ప్రాంతంతోను, కృష్ణాజిల్లా అత్యల్ప అటవీ ప్రాంతాన్ని కల్గి ఉంది.

→ సాంద్రత రీత్యా విశాఖపట్టణం జిల్లా మొదటి స్థానంలోను, కృష్ణాజిల్లా చివరి స్థానంలోనూ ఉంది.

→ ఆంధ్రప్రదేశ్ లో అడవులు ఉత్తరాన సింహాచలం కొండల నుండి దక్షిణాన శేషాచలం కొండల వరకు విస్తరించి ఉన్నాయి.

→ నల్లమల అడవి అతి పెద్ద అటవీ ప్రాంతం.

→ తేమతో కూడిన ఆకురాల్చు అడవులు శ్రీకాకుళం, విజయనగరం, తూర్పు గోదావరి జిల్లాల్లో కలవు.

→ తేమతో కూడిన ఆకురాల్చు అడవుల్లో వేగి, ఏగిస, వెదురు, మద్ది, బండారు – జట్టేగి మరియు సాల వృక్షాలు పెరుగుతాయి.

→ శుష్క ఆకురాల్చు అడవులు YSR కడప, కర్నూలు, అనంతపురం, చిత్తూరు జిల్లాల్లో కలవు.

→ శుష్క ఆకురాల్చు అడవుల్లో ముఖ్య వృక్షాలు మద్ది, టేకు, బిల్లు, వెలగ, ఏగిస, వేప, బూరుగ, మోదుగ మరియు ఎర్రచందనం.

→ ఎర్రచందనం కడప, చిత్తూరు జిల్లాల్లోని శేషాచలం అడవుల్లో పెరిగే అరుదైన వృక్షజాతి. ఎగుమతుల్లో ఆర్థిక వ్యవస్థలో ఈ వృక్షానికి విశేష స్థానం ఉంది.

→ చిట్టడవులు రాయలసీమ జిల్లాలయిన కడప, కర్నూలు, అనంతపురం, చిత్తూరు జిల్లాల్లో పెరుగుతాయి.

→ ‘చిట్టడవుల్లో తుమ్మ, బులుసు, రేగు, చందనం, వేప మొదలగు చెట్లు పెరుగుతాయి. కడప జిల్లాలోని శ్రీలంక మల్లేశ్వర అభయారణ్యంలో నివసించే ‘కలివికోడి’ని IUCN అరుదైన జాతులుగా తెలియజేసింది.

→ మడ/డెల్టా అడవులు ఆంధ్రప్రదేశ్ తీర ప్రాంతం 974 కి.మీ. ఈ తీరం వెంబడి ఈ అడవులున్నాయి.

→ మడ/డెల్టా అడవుల్లో, ఉప్పు పొన్న, బొడ్డు పొన్న, ఉరడ, మడ, తెల్లమడ, పత్రి తీగ, బలబండి తీగ చెట్లు ఇక్కడ పెరుగుతాయి.

→ తూర్పు గోదావరిలోని ‘కోరంగి’ ప్రాంతం మడ అటవీ ప్రాంతానికి చక్కని ఉదాహరణ. వృక్షజాలం, జంతుజాలాలను రక్షించటానికి 13 వన్యప్రాణుల అభయారణ్యాలు మరియు మూడు జాతీయ ఉద్యానవనాలు ఆంధ్రప్రదేశ్ లో స్థాపించబడ్డాయి.

→ బోండోలు, చెంచులు, కొండరెడ్లు, కొండ సవరలు, గోండ్లు, ఎరుకల మరియు యానాదులు ఆదిమజాతులవారు.

→ చెంచులు ఒక ఆదిమ తెగ, వీరు నల్లమల అడవిలో ఉంటారు.

→ బ్రిటీషు వారు 1864లో అటవీశాఖను ఏర్పాటు చేశారు.

→ 1988 జాతీయ అటవీ విధాన ప్రకటన వన సంరక్షణ , పునరుజ్జీవనం, అడవుల అభివృద్ధిలో గిరిజన భాగస్వాములను చేయడం అనేది ముఖ్యమైన అంశంగా ప్రకటించింది.

→ ప్రస్తుతం ఆంధ్రప్రదేశ్ స్థానిక గిరిజనులను భాగస్వామ్యం చేస్తూ ఎకో-టూరిజం విధానాన్ని బలోపేతం చేసింది.

→ బంజరు భూముల్లో, ఇతర ప్రదేశాలలో మొక్కలు నాటడం, అడవులను సంరక్షించడం ద్వారా పర్యావరణాన్ని సామాజిక మరియు గ్రామ అభివృద్ధులను పెంపొందించడం కోసం చేపట్టిన పథకాన్ని “సామాజిక అడవుల” పెంపకం అనవచ్చు.

→ 1894 – అడవుల చట్టం, 1950 – అడవుల పండుగ.
1952 – జాతీయ అటవీ విధానం, 1980 – వన సంరక్షణ చట్టం.
2006 – అటవీ హక్కుల చట్టం.

→ FPST – అటవీ నివాస షెడ్యూల్డ్ తెగలు.
OTFD – ఇతర సాంప్రదాయ అటవీ నివాసులు.

→ అడవుల ఉపయోగాలను నాలుగు రకాలుగా వర్గీకరించవచ్చును. అవి :
1) వినియోగం కొరకు
2) వాణిజ్యం కొరకు
3) పర్యావరణ వ్యవస్థల సమతుల్యం
4) పరిశోధనలు

→ సామాజిక, ఆర్థిక, మత, సాంస్కృతిక, మాండలిక సారూప్యాలు కలిగిన కుటుంబాలలో సంప్రదాయ సమూహాలుగా ఉన్న సామాజిక విభాగాన్ని ‘అటవీ జాతి’ అంటారు.

→ సెల్వాలు : దట్టమైన అడవులతో ఉన్న (భూమధ్య రేఖా ప్రాంతము) ప్రాంతం.

→ పోడు వ్యవసాయం : అడవులను కొంత మేరకు నరికి, కాల్చి గిరిజనులు చేయు వ్యవసాయం.

→ సవన్నాలు : ఉష్ణ మండలపు గడ్డి మైదానాలను సవన్నాలు అంటారు.

→ వాణిజ్య వ్యవసాయం : లాభం కోసం చేసే విస్తార వ్యవసాయం.

→ స్టెప్పీలు : సమశీతోష్ణ మండలపు గడ్డి భూములను స్టెప్పీలు అంటారు.

→ రిజర్వు అడవులు : వేట, మేత నిషేధించిన అడవులు.

→ రక్షిత అడవులు : ప్రత్యేక వృక్షజాలం, జంతు జాలాలను రక్షించటానికి ఏర్పాటు చేయబడ్డ అడవులు.

→ సతతహరిత అడవులు : ఏడాది పొడవునా పచ్చగా ఉండే అడవులు. . * చిత్తడి అడవులు : తీర ప్రాంతపు, మడ అడవులు.

→ ISFR : ఇండియన్ స్టేట్ ఫారెస్ట్ రిపోర్ట్.

→ ఎకో టూరిజం : (పర్యావరణ పర్యాటకం) సామాజిక ఆధారిత పర్యావరణ కేంద్రాల సందర్శనకై ఆంధ్రప్రదేశ్ ప్రభుత్వం ఏర్పాటు చేసిన నూతన విధానం.

→ IUCN : ప్రకృతి మరియు సహజ వనరుల పరిరక్షణ కోసం అంతర్జాతీయ యూనియన్.

→ FDST : అటవీ నివాస షెడ్యూల్డ్ తెగలు.

→ OTFD : ఇతర సాంప్రదాయ అటవీ నివాసులు.

→ అడవి : విశాల ప్రాంతంలో సహజ పరిస్థితులలో చెట్లు, పొదలతో కూడిన నిర్దిష్ట ప్రాంతం.

→ వృక్షజాలం : ఒక ప్రత్యేకమైన ప్రాంతంలో పెరిగే మొక్కలు.

→ జంతుజాలం : ప్రత్యేకమైన ప్రాంతంలో నివసించే జంతువులు.

→ దట్టమైన అరణ్యం : ఒక ప్రాంతంలో చెట్లు దగ్గర దగ్గరగా పెరగడం.

→ శీతోష్ణస్థితి : ఒక ప్రదేశంలోని దీర్ఘకాలపు సగటు వాతావరణపు స్థితి.

→ బాష్పోత్సేకం : చెట్ల నుంచి నీరు ఆవిరి కావడం.

→ సుందరవనాలు : పశ్చిమ బెంగాల్ లో పెరిగే మడజాతి వనాలు.

→ శృంగాకారపు చెట్లు : సూది ఆకారం ఆకులు గల పొదలు.

→ పట్టణీకరణ : ప్రజలు గ్రామీణ ప్రాంతాల నుంచి పట్టణాలకు వలస వెళ్లడం.

→ ఆదిమ వాసులు : ఒక ప్రాంతంలో ప్రాచీన కాలం నుండి నివసించేవారు.

→ భూగోళం వేడెక్కడం : భూ ఉపరితలం వేడెక్కడం.

→ నేల క్రమక్షయం : భూమి యొక్క పై పొరలు క్రమంగా తొలగించబడడం.

1.

2.

3.

Students can go through AP Board 7th Class Social Notes 13th Lesson ప్రపంచ పరివర్తనలో మహిళలు to understand and remember the concept easily.

AP Board 7th Class Social Notes 13th Lesson ప్రపంచ పరివర్తనలో మహిళలు

→ భారతదేశంలో 83, 6% మంది శ్రామిక మహిళలు వ్యవసాయ పనుల్లో నిమగ్నమై ఉన్నారు.

→ మన సమాజంలో మగ పిల్లలకు ఇచ్చినంత ప్రాధాన్యత ఆడపిల్లలకు ఉండదు.

→ 2015లో బాలికల సర్వతోముఖాభివృద్ధికిగాను ‘బేటీ బచావో బేటీ పఢావో’ అనే కార్యక్రమం ప్రారంభించారు.

→ పాఠశాలకు వెళ్ళడం అనేది బాలికల యొక్క ప్రాథమిక హక్కు.

→ ఆంధ్రప్రదేశ్ లో ప్రభుత్వం 1993లో సారాను నిషేధించింది.

→ మార్చి 8వ తేదీన అంతర్జాతీయ మహిళా దినోత్సవం జరుపుకుంటాము.

→ కాదంబరి గంగూలి, చంద్రముఖి బసు భారతదేశంలోని మొదటి ఇద్దరు మహిళా గ్రాడ్యుయేట్లు.

→ జానకి అమ్మాళ్ పద్మశ్రీ అవార్డు అందుకున్న మొదటి భారతీయ మహిళా శాస్త్రవేత్త.

→ అంతరిక్ష రంగంలోకి అడుగుపెట్టిన తొలి భారతీయ మహిళ కల్పనా చావ్లా.

→ కల్పనా చావ్లా 2003లో STS – 107 మిషన్ వైఫల్యం కారణంగా మరణించింది.

→ మహిళల వన్డే ఇంటర్నేషనల్ మ్యాచ్ లో 7,000 పరుగుల మార్కును అధిగమించిన మహిళా క్రికెటర్ ‘మిథాలీరాజ్.

→ మిథాలీ రాజ్ కు ‘లేడీ సచిన్’ అనే ట్యాగ్ ఉంది.

→ మహిళల అంతర్జాతీయ క్రికెట్లో అత్యధిక పరుగులు చేసిన క్రీడాకారిణిగా మిథాలీరాజ్ ప్రసిద్ధి పొందింది.

→ ఈమెకు ‘ఖేల్ రత్న’ పురస్కారం కూడా లభించింది.

→ ప్రాంజల్ పాటిల్ భారతదేశంలో మొదటి దృష్టి లోపం ఉన్న IAS అధికారిణి.

→ సీమారావు దేశంలోనే తొలి మహిళా కమాండో ట్రైనర్.

→ సీమారావు బ్రూస్ లీ అభివృద్ధి చేసిన మార్షల్ ఆర్ట్స్ లో జీత్ కునే డోలో శిక్షణ పొందిన ప్రపంచంలోని 10 మంది మహిళలలో ఒకరు.

→ ‘రాజ్ కుమారి దేవి’ SHG సేవలకుగాను 2019లో పద్మశ్రీ అవార్డు ఇచ్చారు.

→ ‘వందనాశివ’ ఒక పర్యావరణ వేత్త మరియు పర్యావరణ హక్కుల కార్యకర్త, – స్థానిక విత్తనాలను రక్షించటానికి ‘నవధాన్య’ అనే జాతీయ ఉద్యమం ఏర్పడటానికి ‘వందనాశివ’ ప్రయత్నాలు దారితీశాయి.

→ 1993లో రైట్ లైబ్లీ హుడ్ అవార్డును మరియు 2010 సిడ్ని శాంతి బహుమతిని (వందనా శివ) అందుకున్నారు.

→ లక్ష్మీ అగర్వాల్ యాసిడ్ దాడి భాదితురాలు.

→ లక్ష్మీ అగర్వాల్ NGO ఛన్‌ ఫౌండేషన్ కు డైరెక్టర్.

→ లక్ష్మీ అగర్వాల్ US ప్రథమ మహిళ మిచెల్ ఒబామాచే 2014లో ఇంటర్నేషనల్ ఉమెన్ ఆఫ్ కరేజ్ అవార్డును అందుకుంది.

→ ఈమె NDTV ఇండియన్ ఆఫ్ ది ఇయర్‌గా కూడా ఎంపికైంది.

→ నందిని హరినాథ్ ఇస్రో శాటిలైట్ సెంటర్ లో రాకెట్ శాస్త్రవేత్త.

→ ఈమె MOM ప్రాజెక్ట్ మేనేజర్, మిషన్ డిజైనర్ మరియు డిప్యూటీ ఆపరేషన్స్ డైరెక్టర్‌గా పనిచేశారు.

→ ఈమె ఇస్రోలో 20 ఏళ్ళుగా 14 మిషన్లలో పనిచేసారు.

→ UNO ప్రధాన కార్యదర్శిగా ఎంపిక చేసిన వాతావరణ సంక్షోభాన్ని ఎదుర్కోవడానికి పరిష్కారాలను అందించే యువజన సలహా సంఘ సభ్యులు ‘యంగో’లోని 7గురు సభ్యులలో ఒకరిగా ఎంపికైన యువతి ‘అర్చనా సోరెంగ్’.

→ మహనాజ్ అమి రచించిన పుస్తకం – ‘ఎంచుకునే దారిలో’.

→ లింగ వివక్షత : లింగాధారంగా వివక్షతను చూపుట. స్త్రీని తక్కువగాను, పురుషులను ఎక్కువగాను చూడటాన్ని లింగ వివక్షత అంటారు.

→ శారీరక వైకల్యం : శరీరంలోని ఏదైనా భాగం సరిగా పని చేయకపోవటం లేదా అసలు పని చేయకపోవటం.

→ పరివర్తన : ఆలోచనల్లో, మూస పద్ధతులలో మార్పు.

→ మహిళా ఉద్యమం : మూస పద్ధతులలో మార్పు తీసుకురావడానికి మహిళలు వ్యక్తిగతంగా మరియు సమష్టి పోరాటం చేయడమే మహిళా ఉద్యమం.

→ ఆత్మ గౌరవం : వ్యక్తిగతంగా (ఏ వివక్ష చూపకుండా) గౌరవింపబడటం. తనకు తాను గౌరవప్రదంగా ఉండటం.

→ మహిళా సాధికారత : మహిళలు స్వయంగా (ఇతరులపై ఆధారపడకుండా) విభిన్న సమస్యలపై నిర్ణయాలు తీసుకొనుట మరియు వారు కోరుకున్న లక్ష్యాలను సాధించటానికి, కొనసాగించటానికి మరింత స్వేచ్ఛ కల్గి ఉండటం. ఇది రాజకీయ మరియు ఆర్థిక సాధికారతలుగా పేర్కొన్నారు.

→ గిరిజనులు : కొండ (అటవీ) ప్రాంతంలో నివసించేవారు.

→ SHG : స్వయం సహాయక బృందం (Self Help Group)

→ NGO : Non Government Organisation.

→ ISRO : ఇండియన్ స్పేస్ రీసెర్చ్ ఆర్గనైజేషన్

→ మూస పద్ధతి : ఒక నిర్దిష్ట వర్గము లేదా వ్యక్తుల గురించి సాధారణీకరించిన నమ్మకం. ఇది ఒక నిర్దిష్ట సమూహంలోని వ్యక్తి గురించి ప్రజలకు ఉండే భావన.

→ వివక్ష : వ్యక్తులు, సమూహాలు, తరగతులు లేదా ఇతర వర్గాల ఆధారంగా వ్యక్తుల మధ్య అన్యాయమైన వ్యత్యాసాలను చూపే చర్య.

→ లింగ సమానత్వము : స్త్రీలు, పురుషులు అనే భేదభావం లేకుండా సామాన్య హక్కులు, బాధ్యతలు మరియు అవకాశాలు ఉండుట.

→ స్ఫూర్తిదాయక మహిళలు: ఇతరులను ప్రభావితం చేసే వ్యక్తిత్వం ఉన్నవారు.

Students can go through AP Board 7th Class Social Notes 12th Lesson మన పరిసరాలలో ఉన్న మార్కెట్లు to understand and remember the concept easily.

AP Board 7th Class Social Notes 12th Lesson మన పరిసరాలలో ఉన్న మార్కెట్లు

→ రద్దీగా ఉండే వ్యక్తులు, వివిధ రకాల వస్తువులు, పండ్లు, కూరగాయలు మరియు ఆ వస్తువులను కొనుగోలు చేసే వినియోగదారులు మరియు వాటిని విక్రయించే దుకాణాలు ఉండే ప్రాంతం.

→ పని చేసే విధానం ఆధారంగా మార్కెట్లను రెండు రకాలుగా విభజిస్తారు. అవి

1. భౌతిక మార్కెట్లు,
2. ఈ-మార్కెట్లు.

→ భౌతిక మార్కెటు అనేది కొనుగోలుదారులు, అమ్మకందారులు భౌతికంగా కలిసి వారికి అవసరమైన వస్తువులను కొనుగోలు చేసే ప్రాంతం.

→ అమ్మకందారులు మరియు కొనుగోలుదారులు స్థానికంగా ఒక నిర్ణీత ప్రాంతానికి పరిమితమైతే వాటిని స్థానిక మార్కెట్లు అంటారు.

→ స్థానిక మార్కెట్ల కంటే ఎక్కువ విస్తృతి కలిగి వుండి ఆయా ప్రాంతాలలో లేదా రాష్ట్రాల సముదాయంలో మాత్రమే లభించే వస్తువులను కలిగి వుండే మార్కెట్లను ప్రాంతీయ మార్కెట్లు అంటారు.

→ జాతీయ మార్కెట్ అనునది దేశంలోని అన్ని ప్రాంతాలలో వస్తువులు మరియు సేవల కోసం వర్తకం జరిగే మార్కెట్.

→ వివిధ దేశాల మధ్య జరిగే వస్తువులు మరియు సేవల వ్యాపారాన్ని అంతర్జాతీయ మార్కెట్ అంటారు.

→ రైతుబజార్లు జనవరి 1999లో ప్రారంభించబడినవి.

→ పట్టణ ప్రాంతాలలోని వివిధ అంతస్థులలోని దుకాణాలు, పెద్ద బహుళ అంతస్థుల ఎయిర్ కండీషన్డ్ భవనాలు. వీటినే షాపింగ్ మాల్స్ అంటారు.

→ పట్టణాలలో లేదా నగరాలలోని వివిధ ప్రాంతాలలో ఒకే ప్రాంగణంలో అన్ని రకాల వస్తువులను విక్రయించే దుకాణాలు ఉంటాయి. వీటిని షాపింగ్ కాంప్లెళ్లు అంటారు.

→ శ్రీనగర్‌లో ఫ్లోటింగ్ మార్కెట్లో అత్యంత సుందరమైన దాల్ సరస్సులో ఉ|| 5-7 వరకు కూరగాయల వ్యాపారం పడవల ద్వారా జరుగుతుంది.

→ ఈ పడవలను స్థానిక భాషలో ‘షికారా’ అంటారు.

→ మనం మన వద్ద వున్న చరవాణి ద్వారా లేదా అంతర్జాలంతో అనుసంధానమైన కంప్యూటర్ ద్వారా ఆదేశాలు ఇచ్చి మనకు నచ్చిన అనేక రకాలైన వస్తువులను ఇంటి నుండి బయటకు వెళ్ళకుండానే కొనుగోలు చేయవచ్చు. ఈ రకమైన మార్కెట్ ను ఈ-కామర్స్ లేదా ఆన్లైన్ మార్కెట్ అంటారు. ఎలక్ట్రానిక్ కామర్స్ లేదా ఈ-కామర్స్ అనునది ఒక వ్యాపార వేదిక.

→ వినియోగదారుడు అనగా తన వ్యక్తిగత ఉపయోగం కోసం లేదా స్వయం ఉపాధి ద్వారా తన జీవనోపాధిని సంపాదించుకోవడం కోసం, ఒక ఉత్పత్తిని కొనుగోలు చేసే లేదా ఒక సేవను వినియోగించుకొనే వ్యక్తి. వినియోగదారుని హక్కులను రక్షించడానికి రూపొందించిన చట్టాలను వినియోగదారుల రక్షణ చట్టాలు అంటారు.

→ వినియోగదారుల రక్షణ చట్టం ఆగస్టు 9, 2019న ఆమోదించబడింది.

→ వినియోగదారుల రక్షణ చట్టం 1986 ప్రకారం జాతీయ వినియోగదారుల వివాద పరిష్కార కమీషన్ (ఎన్.సి.డి. ఆర్.సి) 1988 లో స్థాపించబడినది.

→ ఎన్.సి.డి.ఆర్.సి ప్రధాన కార్యా లయం కొత్త ఢిల్లీలో ఉంది.

→ వినియోగదారుల హెల్ప్ లైన్ నంబర్ : నేషనల్ టోల్ ఫ్రీ నెంబర్ 1800-114000 లేదా 14404.

→ ప్రతి సంవత్సరం డిసెంబరు 24ను భారతదేశంలో జాతీయ వినియోగదారుల దినోత్సవంగా జరుపుకుంటారు.

→ మార్కెట్ : రద్దీగా ఉండే వ్యక్తులు, వివిధ రకాల వస్తువులు, పండ్లు, కూరగాయలు మరియు ఆ వస్తువులను కొనుగోలు చేసే వినియోగదారులు మరియు వాటిని విక్రయించే దుకాణాలు ఉండే ప్రాంతం.

→ భౌతిక మార్కెట్ : కొనుగోలుదారులు, అమ్మకందారులు భౌతికంగా కలిసి వారికి అవసరమైన వస్తువులను కొనుగోలు చేసే ప్రాంతం.

→ స్థానిక మార్కెట్లు : కొనుగోలుదారులు మరియు అమ్మకందారులు స్థానికంగా వస్తువులు ఉత్పత్తి అయ్యే ఒక నిర్ణీత ప్రాంతానికి పరిమితమైతే వాటిని స్థానిక మార్కెట్లు అంటారు.

→ ప్రాంతీయ మార్కెట్లు : స్థానిక మార్కెట్ల కంటే ఎక్కువ విస్తృతిని కలిగి ఉండి ఆయా ప్రాంతాలలో లేదా రాష్ట్రాల సముదాయంలో మాత్రమే లభించే వస్తువులను కల్గి ఉండే మార్కెట్లు.

→ జాతీయ మార్కెట్లు : జాతీయ మార్కెట్ అనునది దేశంలోని అన్ని ప్రాంతాలలో వస్తువులు మరియు సేవల కోసం వర్తకం జరిగే మార్కెట్. ఉదాహరణకు తీరప్రాంత రాష్ట్రాలలో లభించే చేపలను దేశవ్యాప్తంగా అమ్మడం.

→ అంతర్జాతీయ మార్కెట్లు : వివిధ దేశాల మధ్య జరిగే వస్తువులు మరియు సేవల వ్యాపారాన్ని అంతర్జాతీయ మార్కెట్ అంటారు.

→ పొరుగు మార్కెట్లు : మన ఇంటి పక్కన లేదా వీధి చివరలో కన్పించే దుకాణాలు.

→ వారాంతపు సంత : ప్రతి వారం ఒక నిర్దిష్టమైన రోజున ఉదయాన్నే ఏర్పాటు చేయబడి సాయంత్రం మూసివేయబడే మార్కెట్.

→ క్రెడిట్ కార్డు : ఋణ సౌలభ్యాన్ని వినియోగించుకొని వస్తువులు కొనుగోలు చేయుటకు ఆర్థిక సంస్థలు జారీ చేసే కారు.

→ రైతు బజారు : రైతులే నేరుగా వినియోగదారులకి తమ ఉత్పత్తులు అమ్ముకునే మార్కెట్.

→ షాపింగ్ మాల్స్ : పట్టణ ప్రాంతాలలోని వివిధ అంతస్థులలోని దుకాణాలు, పెద్ద బహుళ అంతస్థుల ఎయిర్ కండీషన్ భవనాలు.

→ ఈ షాపింగ్ కాంప్లెక్స్ : పట్టణాలు మరియు నగరాలలోని వివిధ ప్రాంతాలలో ఒకే ప్రాంగణంలో దాదాపు అన్ని రకాల వస్తువులను విక్రయించే దుకాణాలు.

→ ఫ్లోటింగ్ మార్కెట్ : నీటిలో తేలియాడే మార్కెట్స్.

→ వినియోగదారుల రక్షణ చట్టాలు : వినియోగదారుని హక్కులను రక్షించడానికి రూపొందించిన చట్టాలు.

→ ఉత్పత్తిదారుడు : ఆహారం, వస్తువులు లేదా సామగ్రిని తయారుచేసే ఒక వ్యక్తి, ఒక కంపెనీ లేదా ఒక దేశం.

→ కొనుగోలుదారు : వ్యాపార రీత్యా వస్తువులను పెద్ద మొత్తంలో కొనుగోలు చేయువారు.

→ వ్యాపారి : కొనుగోలు మరియు విక్రయించే వ్యక్తి.

→ టోకు వర్తకుడు : వ్యక్తులకు లేదా సంస్థలకు పెద్ద మొత్తంలో వస్తువులు విక్రయించు వ్యక్తి లేదా సంస్థ.

→ చిల్లర వర్తకుడు : చిన్న మొత్తంలో ప్రజలకు వస్తువులు విక్రయించే వ్యక్తి లేదా వ్యాపారం.

→ వినియోగదారుడు వస్తువులను కొనుగోలు చేసే లేదా సేవలను వినియోగించుకునే వ్యక్తి.

→ క్రెడిట్ : కొనుగోలు చేసిన వస్తువులకు తరువాత చెల్లించే ఏర్పాటు.

→ వృత్తి : జీవనోపాధికై చేసే పని లేదా ఉద్యోగం.

→ సంస్థ : వ్యాపార కార్యకలాపాలు నిర్వహించే యంత్రాంగం.

→ వేదిక : ప్రజల ఫిర్యాదులను విని తీసుకోవాల్సిన చర్యలను సూచించే న్యాయస్థానాలు.

→ అయోగ్యత : అనైతిక లేదా అన్యాయమైన.

Students can go through AP Board 7th Class Social Notes 11th Lesson రహదారి భద్రత to understand and remember the concept easily.

AP Board 7th Class Social Notes 11th Lesson రహదారి భద్రత

→ రహదారి ప్రమాదాలు అనగా ఏదైనా ఆకస్మిక సంఘటన వలన వాహనం లేదా ప్రయాణీకులు ప్రమాదవశాత్తు గాయపడటం లేదా మరణించడం మరియు భౌతిక ఆస్తులకు నష్టం కలగటం వంటివి.

→ నేటి ప్రపంచంలో రోడ్డు మరియు రవాణా ప్రతి మనిషి జీవితంలో అంతర్భాగంగా మారాయి.

→ ప్రస్తుత రవాణా వ్యవస్థ, దూరాలను తగ్గించింది కానీ మరోవైపు అది జీవితాలను ప్రమాదంలో పడవేసింది.

→ ప్రతి సంవత్సరం రోడ్డు ప్రమాదాలు లక్షలాది మంది ప్రాణాలు కోల్పోవడం మరియు కోట్లాదిమంది తీవ్రమైన గాయాలపాలవడానికి కారణమవుతున్నాయి.

→ అవగాహనా రాహిత్యం మరియు అజాగ్రత్త వల్ల ప్రజలు ఎక్కువ ప్రమాదాలకు గురియగుచున్నారు.

→ భారతదేశంలోని రోడ్డు రవాణా మరియు రహదారుల మంత్రిత్వశాఖ ప్రతి సంవత్సరం జనవరి నెలలో రోడ్డు భద్రతా వారోత్సవాలు నిర్వహిస్తుంది.

→ రహదారులపై గేదెలు, మేకలు, గొర్రెలు వంటి జంతువులను యథేచ్ఛగా వదిలివేయుట. దమ్ము చక్రాలతో ట్రాక్టర్లను నడుపుట వంటివి రహదారి ప్రమాదాలకు కారణాలు.

→ ట్రాఫిక్ గుర్తులు 3 రకాలు :

1. తప్పనిసరిగా పాటించవలసిన గుర్తులు,
2. సమాచార గుర్తులు,
3. హెచ్చరిక గుర్తులు.

→ తప్పనిసరిగా పాటించవలసిన గుర్తులు ఎర్ర వృత్తాలు ఏమి చేయకూడదో తెలుపుతాయి.

→ సమాచార గుర్తులు – నీలం రంగు దీర్ఘచతురస్రంలోని గుర్తులు తెలియజేస్తాయి.

→ హెచ్చరిక గుర్తులు – ముక్కోణం లోపల ఉన్న గుర్తులు హెచ్చరిస్తాయి.

→ ట్రాఫిక్ లైట్ రంగు సంకేతాలు – ఎరుపు – ఆగండి, ఆరెంజ్ – వెళ్ళడానికి సిద్ధంగా ఉండండి; ఆకుపచ్చ – వాహనం ముందుకు వెళ్ళడానికి.

→ ఫుట్ పాత్, పాదచారుల ఉపయోగం కోసం రహదారికి ఇరువైపుల వేయబడింది.

→ ఒకే రహదారిపై ట్రాఫిక్ యొక్క రెండు దిశలను వేరు చేయడానికి రహదారిని రెండు భాగాలుగా విభజించారు. దీనిని రోడ్ డివైడర్ అంటారు.

→ జీబ్రా క్రాసింగ్ అంటే పాదచారులు రహదారిని సురక్షితంగా దాటే ప్రదేశం.

→ డ్రైవింగ్ లైసెన్స్ లేకుండా వాహనం నడపడం నేరం.

→ రహదారి భద్రత : రహదారి వాడకంలో వినియోగదారుల భద్రతను సూచిస్తుంది.

→ ఫుట్ పాత్ : రహదారికి ఇరువైపులా పాదచారులు నడవటానికి వీలుగా ఉండే దారి.

→ ఎరుపురంగు : గీత ముందు ఆగాలని సూచిస్తుంది.

→ ఆరెంజ్ రంగు : వెళ్ళడానికి సిద్ధంగా ఉండాలని సూచిస్తుంది.

→ ఆకుపచ్చ రంగు : వాహనాన్ని కదిలించమని సూచిస్తుంది.

→ ట్రాఫిక్ విద్య : ట్రాఫిక్ నియమ నిబంధనలు సరళంగా, స్పష్టంగా తెలియజేయటం.

→ ట్రామా కేర్ : స్వల్ప లేక తీవ్ర గాయాలపాలైన క్షతగాత్రులకు హాస్పిటల్ కి తీసుకువెళ్ళిన వెంటనే ఇచ్చే తక్షణ చికిత్స.

→ ప్రథమ చికిత్స : ప్రమాదానికి గురైన వ్యక్తికి పూర్తి వైద్య సహాయం అందేలోగా ఇచ్చే ప్రాథమిక వైద్యం.

→ రోడ్డు డివైడర్ : ఇది సిమెంట్ దిమ్మలతో లేదా పెయింట్ తో రోడ్డును రెండు లేదా అంతకంటే ఎక్కువ భాగాలుగా విభజించేది.

→ జీబ్రా క్రాసింగ్ : ఇవి రోడ్డుకు సమాంతరంగా చిత్రించిన ప్రత్యామ్నాయ నలుపు మరియు తెలుపు చారలు. సాధారణంగా వీటిని జీబ్రా క్రాసింగ్ అని పిలుస్తారు. ఇది పాదచారులు రోడ్డును ఒక వైపు నుండి మరొక వైపుకు దాటడానికి ఉద్దేశించబడింది.

→ రైల్వే క్రాసింగ్ : రహదారి, రైల్వే లైనను కలిసే ప్రదేశం.

→ ట్రాఫిక్ : వ్యక్తులు, వస్తువులు, వాహనాలు మరియు పాదచారులు ఒక ప్రదేశం నుండి మరొక ప్రదేశానికి పయనించేటప్పుడు ఏర్పడే రద్దీ.

→ పాదచారి : కాలి నడకన ప్రయాణించే వ్యక్తి.

→ రోడ్డు ప్రమాదం : ఒక వాహనం మరొక వాహనాన్ని లేదా వస్తువును ఢీ కొట్టడం.

→ కెర్బ్ డ్రిల్ : చిన్న పిల్లలు రహదారిని దాటుటకు ఆచరించాల్సిన పద్ధతి.

→ డ్రైవింగ్ లైసెన్స్ : వాహనాలను నడిపే నియమ నిబంధనలను పరిశీలించి ఇచ్చే అనుమతి పత్రం. వాహనదారులు దీనిని తప్పక పొందవలసి ఉంటుంది.

→ R.T.A. కార్యాలయం : Regional Transport Authority Office రీజనల్ ట్రాన్స్ పోర్ట్ అథారిటీ అధికారి వారి కార్యాలయము.

Students can go through AP Board 7th Class Social Notes 10th Lesson రాష్ట్ర ప్రభుత్వం to understand and remember the concept easily.

AP Board 7th Class Social Notes 10th Lesson రాష్ట్ర ప్రభుత్వం

→ భారతదేశంలో మనకు రెండు స్థాయిలలో ప్రభుత్వం ఉంది. ఒకటి కేంద్రంలో, మరొకటి రాష్ట్రంలో ఉంది.

→ రాష్ట్ర ప్రభుత్వం ఆ రాష్ట్ర పరిపాలనకు బాధ్యత వహిస్తుంది.

→ రాష్ట్ర ప్రభుత్వం మూడు అంగాల ద్వారా పరిపాలన నిర్వహిస్తుంది.
అవి

1. శాసన నిర్మాణ శాఖ,
2. కార్య నిర్వాహక శాఖ,
3. న్యాయ శాఖ. గవర్నరు.

→ శాసనసభ మరియు శాసన మండలిలను కలిపి శాసన నిర్మాణ శాఖ అంటారు.

→ చట్టాలను తయారుచేయడం శాసన నిర్మాణ శాఖ యొక్క ప్రాథమిక విధి.

→ భారతదేశంలో ప్రతి రాష్ట్రానికి ఒక గవర్నరు ఉంటారు.

→ ప్రధాన మంత్రి, కేంద్ర మంత్రి మండలి సిఫారసు మేరకు రాష్ట్రపతి అయిదు సంవత్సరాల పదవీ కాలానికి గవర్నర్ ని నియమిస్తారు.

→ ఆర్టికల్ 158 (33) ప్రకారం రెండు లేక ఎక్కువ రాష్ట్రాలకు ఒకే వ్యక్తిని గవర్నర్ గా నియమించవచ్చు.

→ అన్ని అసెంబ్లీ నియోజక వర్గాలకు కేంద్ర ఎన్నికల సంఘం ఎన్నికలు నిర్వహిస్తుంది.

→ MLA – శాసన సభ సభ్యుడు.

→ MLC – శాసన మండలి సభ్యుడు.

→ శాసన మండలి పరోక్షంగా ఎన్నుకోబడిన వారితో పనిచేస్తుంది.

→ 6 సంవత్సరాల పదవీ కాలం ముగిసిన 1/3 వ వంతు సభ్యులు పదవీ విరమణ చేయగా కొత్త సభ్యులు ఎన్నికవుతారు.

→ ఆర్టికల్ 171 (1) ప్రకారం ఒక రాష్ట్ర శాసన మండలి సభ్యుల సంఖ్య, ఆ రాష్ట్ర శాసనసభ సభ్యుల సంఖ్యలో 1/4 వ వంతుకు మించరాదు.

→ 1/12 వ వంతు మంది సభ్యులు ఉపాధ్యాయులచే ఎన్నుకోబడతారు.

→ శాసన సభకు ఆర్థికపర అంశాలలో ఎక్కువ అధికారాలు కలవు.

→ గవర్నర్ రాష్ట్రానికి అధిపతి.

→ గవర్నర్ అనుమతి తర్వాత మాత్రమే అన్ని బిల్లులు చట్టంగా మారతాయి.

→ ఆర్టికల్ 163 (1) ప్రకారం గవర్నర్ తన విధులను నిర్వర్తించడంలో సహాయపడడానికి మరియు సలహా ఇవ్వడానికి ముఖ్యమంత్రి నాయకత్వంలోని మంత్రి మండలి ఉండాలి.

→ ముఖ్యమంత్రి క్యాబినెట్ సభ్యులకు వివిధ మంత్రిత్వ శాఖలను కేటాయిస్తారు.

→ హైకోర్టు రాష్ట్ర స్థాయిలో అత్యున్నత న్యాయ విభాగం. రాష్ట్రంలోని చట్టాల అమలుకు బాధ్యత వహిస్తుంది.

→ భారత రాష్ట్రపతి హైకోర్టు ప్రధాన న్యాయమూర్తిని నియమిస్తారు, పదవీకాలం – 62 సంవత్సరాలు.

→ కేంద్ర, రాష్ట్ర ప్రభుత్వ విధులు/అధికారాలు మూడు జాబితాలుగా విభజించబడ్డాయి.

1. కేంద్ర జాబితా,
2. రాష్ట్ర జాబితా,
3. ఉమ్మడి జాబితా.

→ సాధారణంగా అధికార పక్షానికి చెందిన సభ్యుడు రాష్ట్ర శాసనసభ లేక శాసనమండలిలో బిల్లును ప్రవేశపెడతారు.

→ ఆర్థిక బిల్లును గవర్నరు ముందస్తు అనుమతి పొందిన తరువాత మాత్రమే శాసనసభలో ప్రవేశపెడతారు.

→ రెండు సభల ఆమోదం, గవర్నర్ ఆమోదం తెలిపి సంతకం చేసిన తరువాతనే బిల్లు చట్టంగా మారుతుంది.

→ చట్టాన్ని ‘గెజిట్’లో ప్రచురిస్తారు.

→ జిల్లా కలెక్టర్, జిల్లా పరిపాలనకు అధిపతి.

→ జిల్లా స్థాయిలో ఉన్న కోర్టును జిల్లా కోర్టు అంటారు.

→ ప్రత్యామ్నాయ వివాద పరిష్కార యంత్రాంగాలలో లోక్ అదాలత్ ఒకటి.

→ లోక్ అదాలత్ కు లీగల్ సర్వీస్ అథారిటీస్ యాక్ట్ – 1987 ప్రకారం- చట్టబద్ధమైన హోదా ఇవ్వబడింది.

→ తహసీల్దార్ మండల స్థాయిలో ముఖ్య పరిపాలనా కార్యనిర్వాహణాధికారి.

→ గ్రామ రెవెన్యూ అధికారి గ్రామ స్థాయి పరిపాలనలో ముఖ్య పరిపాలనా కార్యనిర్వాహక అధికారి.

→ ప్రభుత్వం : ప్రభుత్వం అనేది రాజ్యం యొక్క ఒక లక్షణం. ఒక చట్టపరమైన నిర్మితి లేదా వ్యవస్థ. వివిధ విభాగాలతో నిర్దేశింపబడిన అధికార విధులను ప్రభుత్వం కొనసాగిస్తుంది.

→ శాసన నిర్మాణ శాఖ : చట్టాలు శాసనాలను తయారు చేసే శాఖ.

→ కార్యనిర్వాహక శాఖ : చట్టాలను శాసనాలను అమలు చేయు శాఖ.

→ న్యాయశాఖ : ప్రభుత్వం చేసిన చట్టాలు శాసనాలను వ్యాఖ్యానించడంతో పాటు వాటిని పరిరక్షించడం, అమలుకు బాధ్యత వహించు శాఖ.

→ సాధారణ ఎన్నికలు : శాసన సభ(ల) పదవీ కాలం పూర్తయిన తరువాత ఎన్నిక కోసం నిర్వహించే ఎన్నికలు.

→ : ఇది శాసనపరమైన/చట్టపరమైన ప్రతిపాదనల ముసాయిదా.

→ MLA : శాసన సభ సభ్యుడు (Member of Legislative Assembly).

→ MLC : శాసన మండలి సభ్యుడు (Member of Legislative Council).

→ ఎన్నికల సంఘం : దేశంలో / రాష్ట్రంలో ఎన్నికలు నిర్వహించు రాజ్యాంగబద్ధ సంస్థ.

→ మెజారిటీ : ఎక్కువ ఓట్లు / సీట్లు వచ్చినవారు.

→ అధికార పార్టీ : ప్రజాస్వామ్య వ్యవస్థలో శాసనసభకు (చట్ట సభలకు) జరిగిన ఎన్నికల్లో మెజారిటి పొంది, అధికారం పొందిన పార్టీ.

→ ప్రతిపక్ష పార్టీ : రాజకీయంగా ఒకటి లేదా అంతకంటే ఎక్కువగానీ పార్టీలు అధికార పార్టీని వ్యతిరేకించే పార్టీలు.

→ సార్వత్రిక వయోజన ఓటు హక్కు : ఒక నిర్దిష్ట వయస్సు (18 సం||) నిండిన పౌరులందరికి ఏవిధమైన వివక్షత లేకుండా ఓటు హక్కు కల్పించడం.

→ రహస్య ఓటింగ్ విధానం : ఎన్నికల సమయంలో ఓటరు తను ఓటు వేసే విషయంలో గోప్యతను కల్గి ఉండటం.

→ లోక్ అదాలత్ : ప్రజా న్యాయ స్థానం, ప్రత్యామ్నాయ వివాద పరిష్కార యంత్రాంగంలో ఒకటి.

→ సివిల్ వివాదాలు : వ్యక్తుల మధ్య ఒప్పందాలు/నియమాల ఉల్లంఘన వల్ల ఏర్పడే వివాదం.
ఉదా : భూ, ఆస్తి, విడాకులు, అద్దె మొదలైనవి.

→ క్రిమినల్ వివాదాలు : చట్ట ఉల్లంఘనకు పాల్పడితే పోలీసులు పెట్టే కేసులు. ఉదా : దొంగతనం, లంచం, హత్య, దోపిడీ, లంచాలు ఇవ్వటం మొదలైనవి.

→ మేజిస్టీరియల్ అధికారాలు : న్యాయ, శాంతి భద్రతలకు సంబంధించిన అధికారాలు.

→ సుప్రీం కోర్టు : దేశంలోని అత్యున్నత న్యాయస్థానం.

→ హైకోర్టు : రాష్ట్రంలోని అత్యున్నత న్యాయస్థానం.

→ జిల్లా కోర్టు : జిల్లా స్థాయిలో అత్యున్నత న్యాయస్థానం.

→ CPC : సివిల్ ప్రొసీజర్ కోడ్.

→ CrPC : క్రిమినల్ ప్రొసీజర్ కోడ్.

→ నియోజక వర్గం : ఒక ప్రాంత పరిధిలో నివసిస్తున్న ఓటర్లందరూ తమ ప్రతినిధులను ఎన్నుకునే ఒక నిర్దిష్ట ప్రాంతం.

→ ద్విసభా వ్యవస్థ : రెండు శాసనసభలతో కూడిన ప్రభుత్వాన్ని ద్విసభా వ్యవస్థ అంటారు.

→ గెజిట్ : ప్రభుత్వ చర్యలు మరియు నిర్ణయాలను తెలియజేసే అధికారిక ప్రచురణ.

→ సమన్స్ : సభ సభ్యులందరినీ సమావేశపరచటం.

→ ప్రోరోగ్ : సభను నిరవధికంగా వాయిదా వేయడం.

→ బ్యూరోక్రసి : ప్రభుత్వ ఉద్యోగులు కీలక విధాన నిర్ణేతలుగా ఉన్న ప్రభుత్వ వ్యవస్థ.

→ సయోధ్య / రాజీ కుదుర్చుకోవడం : న్యాయస్థానాల ప్రమేయం లేకుండా మధ్యవర్తుల ద్వారా వివాదాలు పరిష్కరించుకోవడం.

→ సర్వే రాళ్ళు : భూ సరిహద్దులను నిర్ణయించడం కొరకు ఏర్పాటు చేయబడిన గుర్తులు.

→ మ్యానిఫెస్టో : ఎన్నికల ముందు రాజకీయ పార్టీలు ప్రకటించే హామీల పత్రం.

→ సమావేశపరచడం : శాసనసభ సభ్యులందరినీ సమావేశపరచడం.

→ సంకీర్ణం : ప్రభుత్వ ఏర్పాటు కోసం రాజకీయ పార్టీలు కలవడం.

1.

2.

Students can go through AP Board 7th Class Social Notes 9th Lesson భారత రాజ్యాంగం – పరిచయం to understand and remember the concept easily.

AP Board 7th Class Social Notes 9th Lesson భారత రాజ్యాంగం – పరిచయం

→ బ్రిటిషు పార్లమెంటు చేసిన చట్టాలలో, భారత ప్రభుత్వ చట్టం-1935 చాలా ముఖ్యమైన చట్టం.

→ 1928వ సంవత్సరంలో భారతదేశానికి రాజ్యాంగాన్ని రూపొందించడానికి భారత జాతీయ కాంగ్రెస్ సహా అన్ని పార్టీలు ఒక కమిటీని ఏర్పాటు చేసాయి.

→ ఈ కమిటీ చైర్మన్ గా మోతీలాల్ నెహ్రూ వ్యవహరించారు.

→ ఈ కమిటీ తన నివేదికను 1929వ సం||లో సమర్పించింది.

→ దీనిని నెహ్రూ నివేదిక అని పిలుస్తారు. ఇది మొదటి రాజ్యాంగపత్రంగా పరిగణించబడుతుంది.

→ 1931వ సం||లో, కరాచీలో జరిగిన భారత జాతీయ కాంగ్రెస్ సమావేశం స్వతంత్ర భారతదేశం యొక్క రాజ్యాంగం ఎలా ఉండాలో ఒక తీర్మానాన్ని ఆమోదించింది.

→ నెహ్రూ నివేదిక మరియు కరాచీ తీర్మానం రెండూ సార్వత్రిక వయోజన ఓటు హక్కు స్వేచ్ఛ మరియు సమానత్వ హక్కుకు కట్టుబడి ఉన్నాయి.

→ భారత జాతీయ కాంగ్రెస్ ను 1885వ సంవత్సరంలో స్థాపించారు.

→ రాజ్యాంగాన్ని రూపొందించడానికి, ఎన్నుకోబడిన ప్రతినిధుల చేత ఏర్పడిన సభనే ‘రాజ్యాంగ సభ’ అంటారు.

→ 1946 కెబినేట్ మిషన్ ప్లాన్ ప్రకారం రాజ్యాంగ సభకు జూలై, 1946లో ఎన్నికలు జరిగాయి.

→ బ్రిటిషు పాలనలో ఉన్న రాష్ట్రాలు లేదా ప్రాంతాల నుండి 292 మంది సభ్యులను ఎన్నుకున్నారు.

→ స్వదేశీ సంస్థానాలు అన్ని కలిసి 93 మంది సభ్యులను సిఫార్సు చేసాయి.

→ ఢిల్లీ, అజ్మీర్ – మేవాడ్, కూర్గ్ మరియు బ్రిటిషు బెలూచిస్తాన్ నుండి నలుగురు సభ్యులను ఎన్నుకున్నారు.

→ దీంతో భారత రాజ్యాంగ సభ మొత్తం సభ్యుల సంఖ్య 389కి చేరుకున్నది.

→ ఈ 389 మంది సభ్యులలో 26 మంది షెడ్యూల్డ్ కులాలకు చెందినవారు, 9 మంది మహిళా సభ్యులు కలరు.

→ 1947 ఆగస్టులో దేశ విభజనతో రాజ్యాంగ సభను భారత రాజ్యాంగ సభ మరియు పాకిస్తాన్ రాజ్యాంగ సభగా విభజించారు.

→ భారత రాజ్యాంగ సభలో 299 మంది సభ్యులున్నారు.

→ డా|| బాబు రాజేంద్రప్రసాద్ రాజ్యాంగ సభ అధ్యక్షునిగా, తరువాత మొదటి రాష్ట్రపతిగా ఎన్నికయ్యారు.

→ రెండోసారి రాష్ట్రపతిగా ఎన్నికైన ఏకైక వ్యక్తి డా॥ బాబు రాజేంద్రప్రసాద్ (1950-1962).

→ 1947, ఆగస్టు 29న డా|| B.R. అంబేద్కర్ అద్యక్షతన, ఏడుగురు సభ్యులతో కూడిన ముసాయిదా కమిటీని ఏర్పాటు చేసారు.

→ ముసాయిదా రాజ్యాంగాన్ని తయారుచేసి 1948లో రాజ్యాంగ సభకు సమర్పించారు.

→ ముసాయిదా రాజ్యాంగంలో 315 ప్రకరణలు మరియు ‘8’ షెడ్యూలు ఉన్నాయి.

→ రాజ్యాంగ సభ చేత 1949, నవంబర్ 26న భారత రాజ్యాంగం ఆమోదించబడి, 1950, జనవరి 26న అమల్లోకి వచ్చింది.

→ డా|| బి. ఆర్. అంబేద్కరను “భారత రాజ్యాంగ పిత”గా అభివర్ణిస్తారు.

→ డా|| బి.ఆర్. అంబేద్కర్ 1947లో స్వతంత్ర భారతదేశపు మొట్టమొదటి న్యాయశాఖామంత్రిగా నియమించబడ్డారు.

→ డా|| బి.ఆర్. అంబేద్కర్ 14 ఏప్రిల్, 1891న సెంట్రల్ ప్రావిన్సెస్లో జన్మించారు.

→ భారతదేశంలో రాజ్యాంగ దినోత్సవం ప్రతి సంవత్సరం నవంబర్ 26న జరుపుకొంటాము.

→ రాజ్యాంగ సభ మన రాజ్యాంగాన్ని తయారుచేయడానికి 2 సంవత్సరాల, 11 నెలల 18 రోజులు పట్టింది.

→ రాజ్యాంగం కలిగి ఉన్న ఉపోద్ఘాతమును ‘రాజ్యాంగ పీఠిక’ అంటారు.

→ 13 – 12 – 1946 న రాజ్యాంగ సభ ప్రారంభ సమావేశంలో జవహర్‌లాల్ నెహ్రూ “లక్ష్యాల తీర్మానం”ను ప్రతిపాదించాడు. ఇదే రాజ్యాంగ పీఠికకు మూల ఆధారం.

→ ‘సామ్యవాదం’, ‘లౌకిక’ పదాలు 1976లో 42వ రాజ్యాంగ సవరణ ద్వారా పీఠికలో చేర్చబడ్డాయి.

→ హక్కులు అనేవి వ్యక్తుల సహేతుకమైన వాదనలు.

→ ప్రాథమిక హక్కులనేవి ఒక దేశం తన పౌరులను రక్షించడానికి రాజ్యాంగం ప్రకారం గుర్తించబడినవి.

→ భారత రాజ్యాంగంలో 3వ భాగంలో, ఆర్టికల్ 14 నుండి 32 వరకు ఆరు ప్రాథమిక హక్కులు ఉన్నాయి.

→ సమానత్వపు హక్కు (ప్రకరణ 14-18) అంటరానితనం రద్దు, బిరుదులు రద్దు అనే అంశాలు కలవు.

→ స్వేచ్ఛా హక్కు (ప్రకరణ 19-22) ఆరు రకాలైన స్వేచ్చలకు హామీ ఇస్తుంది.

→ పీడనాన్ని నిరోధించే హక్కు (ప్రకరణ 23-24) వెట్టి చాకిరి, బాల కార్మిక వ్యవస్థను నిషేధిస్తుంది.

→ మత స్వాతంత్ర్యపు హక్కు (ప్రకరణ 25-28) మత వ్యవహారాల్లో ప్రభుత్వం తటస్థంగా ఉంటుంది.

→ విద్యా సాంస్కృతికపు హక్కు (ప్రకరణ 29-30) మత, భాషా ప్రాతిపదికన విద్యా సంస్థలను ఏర్పాటు చేసుకునే హక్కు.

→ రాజ్యాంగ పరిహారపు హక్కు (ప్రకరణ 31-32) అన్ని ప్రాథమిక హక్కులను పరిరక్షించే హక్కు.

→ సమాచార హక్కు చట్టాన్ని (RTI) భారత పార్లమెంట్ 2005లో ఆమోదించింది.

→ 2002లో 86వ రాజ్యాంగ సవరణ ద్వారా భారత పార్లమెంట్ ఆమోదంతో రాజ్యాంగంలో విద్యను ప్రాథమిక హక్కుగా చెప్పే 21-A ప్రకరణను చేర్చారు.

→ బాలల ఉచిత మరియు నిర్బంధ విద్యాహక్కు చట్టాన్ని 2009లో భారత పార్లమెంటు ఆమోదించింది. ఈ చట్టం ఏప్రిల్ 1, 2010న అమల్లోకి వచ్చింది.

→ పౌరులందరి నైతిక బాధ్యతలుగా ‘విధులను’ నిర్వచించారు.

→ ప్రాథమిక విధులను 1976లో 42వ రాజ్యాంగ సవరణ ద్వారా మన రాజ్యాంగంలోని ఆర్టికల్ 51ఎ, భాగం-43. లో పొందుపరిచారు.

→ ఈ ప్రాథమిక విధులు ‘రష్యా’ రాజ్యాంగం నుండి స్వీకరించబడ్డాయి.

→ విలువలు వ్యక్తుల ప్రవర్తనను నిర్ణయించే అంతర్గత ప్రమాణాలు. ఇవి మన చర్యలను ప్రేరేపిస్తాయి.

→ రాజ్యాంగం : దేశం యొక్క స్వభావం, ప్రభుత్వ రూపం, పౌరుల హక్కులు మరియు విధులను తెలియజేసే నిబంధనలతో కూడిన ప్రాథమిక చట్టం.

→ సర్వసత్తాక : బాహ్య మరియు అంతర్గత విషయాలపై నిర్ణయం తీసుకునే పూర్తి అధికారం.

→ సామ్యవాదం : సమాజంలో సామాజిక, ఆర్థిక మరియు రాజకీయ అసమానతలు తగ్గించడం ద్వారా సామాజిక న్యాయం అందించటం.

→ లౌకికవాదం : మత వ్యవహారాలలో ప్రభుత్వం జోక్యం చేసుకోకుండా తటస్థంగా ఉండటం.

→ ప్రజాస్వామ్యం : ప్రజలచే ఎన్నుకోబడిన ప్రజాప్రతినిధులచే ప్రభుత్వం నడపబడటం.

→ గణతంత్ర వ్యవస్థ : రాజ్యా ధినేత ప్రతి ఎన్నికల ద్వారా ఎన్నుకోబడితే అది గణతంత్ర వ్యవస్థ.

→ ప్రకరణ : (అధికరణ) రాజ్యాంగంలోని ఒక నిర్దిష్ట అంశంపై నిర్దిష్ట నియమం లేదా సూత్రాన్ని సూచిస్తుంది.

→ భాగం : ఒక భావనకు సంబంధించిన ప్రకరణల సముదాయమును సూచిస్తుంది.

→ షెడ్యూలు : ప్రకరణలలో పేర్కొనబడని అదనపు సమాచారం లేదా వివరాలను సూచిస్తుంది.

→ ప్రాథమిక హక్కులు : ఒక దేశం తన పౌరులను రక్షించడానికి రాజ్యాంగం ప్రకారం గుర్తించబడినవి.

→ హక్కులు : వ్యక్తుల సహేతుకమైన వాదనలు.

→ విధులు : పౌరుల యొక్క నైతిక బాధ్యతలు

→ రాజ్యాంగ సభ : రాజ్యాంగాన్ని రూపొందించడానికి, ఎన్నుకోబడిన ప్రతినిధులచే ఏర్పడిన సభ.

→ ముసాయిదా కమిటి : ముసాయిదా రాజ్యాంగాన్ని తయారు చేసే కమిటి. అంటే రాజ్యాంగాన్ని రాజ్యాంగ సభ ఆమోదించక ముందు సభ సూచనలను గ్రంథస్తం చేయటం.

→ రాజ్యాంగ పీఠిక : రాజ్యాంగానికి ముందు మాట, ఉపోద్ఘాతం లాంటిది.

→ వయోజన ఓటు హక్కు : ఒక నిర్దిష్ట వయస్సు కల్గిన వారికి కల్పించే ఓటు హక్కు.

→ రాజ్యాంగ సవరణ : ఒక దేశ రాజ్యాంగాన్ని సవరించడం.

→ సౌభ్రాతృత్వం : సోదర భావంతో కలిసి ఉండటం.

→ ప్రావిన్స్ : బ్రిటిష్ పాలనలో, భారతదేశంలోని పరిపాలనా విభాగం.

→ స్వదేశీ సంస్థానం : ఇవి బ్రిటిష్ కాలంలో స్వదేశీ రాజ్యాలు.

→ పౌరుడు : ఒక రాష్ట్రం లేదా దేశంలో సభ్యుడు మరియు అక్కడ చట్టపరమైన హక్కులు ఉన్న వ్యక్తి.

→ పౌరసత్వం : ఒక నిర్దిష్ట దేశంలో పౌరుడికి ఉన్న స్థానం లేదా స్థితి.

→ సమాఖ్య : కేంద్ర ప్రభుత్వం మరియు రాష్ట్ర ప్రభుత్వం మధ్య అధికార పంపిణీ.

→ ద్వంద్వ ప్రభుత్వం : రెండు వ్యవస్థలకు పాలనాధికారం ఉన్న ప్రభుత్వ విధానం.

1.

2.

3.

Students can go through AP Board 7th Class Social Notes 8th Lesson భక్తి – సూఫీ to understand and remember the concept easily.

AP Board 7th Class Social Notes 8th Lesson భక్తి – సూఫీ

→ భక్తి ఉద్యమం 8వ శతాబ్దంలో మొదలై 17వ శతాబ్దం వరకు కొనసాగింది.

→ భక్తి అంటే దేవుని యందు ప్రేమ.

→ భక్తి రెండు రకాలుగా ఉంటుంది. అది సగుణ భక్తి, నిర్గుణ భక్తి.

→ సగుణ భక్తి అనగా భగవంతుని ఒక ఆకారంలో పూజించడం.

→ నిర్గుణ భక్తి అనగా భగవంతుని నిరాకారంగా పూజించడం.

→ భక్తి ఉద్యమాన్ని ఆదిశంకరాచార్యులు ప్రారంభించారు.

→ ఆదిశంకరాచార్యులు కేరళలోని కాలడి గ్రామంలో జన్మించారు. వీరు అద్వైత సిద్ధాంతాన్ని ప్రబోధించారు.

→ వివేక చూడామణి, సౌందర్యలహరి, శివానందలహరి, ఆత్మబోధలు ఆదిశంకరాచార్యుల వారి రచనలు.

→ రామానుజాచార్యులు శ్రీ పెరంబుదూలో క్రీ.శ. 1017లో జన్మించాడు.

→ రామానుజాచార్యులు విశిష్టాద్వైతాన్ని ప్రబోధించారు. శ్రీభాష్యం పేరుతో బ్రహ్మ సూత్రాలమ వ్యాఖ్యానించారు.

→ మధ్వాచార్యులు ద్వైత సిద్ధాంతాన్ని ప్రాచుర్యంలోకి తెచ్చారు. ద్వైతమనగా రెండు అని అర్థం. దీని ప్రకారం బ్రహ్మ మరియు ఆత్మ రెండూ వేర్వేరు అంశాలు.

→ వల్లభాచార్యుల ఆలోచనా విధానాన్ని శుద్ద అద్వైతమంటారు.

→ రామానందుడు ప్రయాగలో జన్మించారు.

→ రామానందుని శిష్యుడు కబీర్.

→ హిందూ ముస్లింల సమైక్యత కొరకు ప్రయత్నించిన మొదటి సాధువుగా కబీర్ ని చెప్పవచ్చు.

→ సంత్ రవిదాస్ బెనారస్లో నివసించారు. “హరిలో అందరూ, అందరిలోనూ హరి” అనేది వీరి బోధనల సారాంశం.

→ మీరాబాయి రాజ కుటుంబంలో జన్మించి కృష్ణ భక్తి తత్వాన్ని ప్రచారం చేసింది.

→ మీరాబాయి సంత్ రవిదాస్ యొక్క శిష్యురాలు.

→ చైతన్య మహాప్రభుని ‘శ్రీ గౌరంగ’ అని కూడా పిలుస్తారు.

→ శంకర దేవుడు అస్సాం ప్రాంత సాధువు.

→ శంకరదేవుడు సాంఘిక, ఆధ్యాత్మిక కార్యక్రమాలకు అన్ని వర్గాల ప్రజలు సమావేశమవడానికి సత్రాలు లేక మఠములు మరియు నామ ఘర్లను ప్రారంభించాడు.

→ సిక్కు మత స్థాపకుడు గురునానక్, కబీర్ బోధనలను ఈయన విశేషంగా అభిమానించాడు.

→ గురునానక్ లాహోర్ సమీపంలోని ‘తల్వండి’ గ్రామంలో క్రీ.శ. 1469లో జన్మించాడు.

→ జ్ఞానేశ్వర్ ‘భగవత్ దీపిక’ పేరుతో భగవద్గీతకు వ్యాఖ్యానాన్ని రాశాడు. దీనినే ‘జ్ఞానేశ్వరి’ అని కూడా అంటారు.

→ జ్ఞానేశ్వర్ మరాఠీ భాషలో బోధనలు చేశాడు.

→ మొల్లమాంబ ప్రసిద్ధ తెలుగు కవయిత్రి. రామాయణాన్ని తెలుగులో రాసింది.

→ తాళ్ళపాక అన్నమాచార్యగా ప్రసిద్ధిగాంచిన అన్నమయ్య కడప జిల్లాలోని తాళ్ళపాక గ్రామంలో జన్మించాడు.

→ అన్నమయ్యను పద కవితా పితామహుడు అంటారు.

→ అన్నమయ్య శ్రీవేంకటేశ్వరుడిని కీర్తిస్తూ 32 వేల సంకీర్తనలు రాశారని ప్రతీతి.

→ ఇస్లాం మతంలోని సాంఘిక మత సంస్కరణ ఉద్యమాన్ని ‘సూఫీ ఉద్యమం’ అంటారు.

→ సూఫీ అనే పదం ‘సాఫ్’ అనే అరబిక్ పదం నుంచి గ్రహించబడింది. సాఫ్ అనగా స్వచ్ఛత లేదా శుభ్రత.

→ ఖ్వాజా మొయినుద్దీన్ చిస్తీ భారతదేశానికి చెందిన గొప్ప సూఫీ సాధువు.

→ ఖ్వాజా మొయినుద్దీన్ చిస్తీ ద్వారా భారతదేశంలో ‘చిస్తీ’ పద్దతి స్థాపించబడింది.

→ ఖ్వాజా మొయినుద్దీన్ చిస్తీ క్రీ.శ. 1143లో పర్షియాలోని ‘సీయిస్థాన్’లో జన్మించారు.

→ ఖ్వాజా మొయినుద్దీన్ చిస్తీ క్రీ.శ. 1192లో భారతదేశాన్ని సందర్శించారు.

→ ఖ్వాజా మొయినుద్దీన్ చిస్తీ వారి దర్గా రాజస్థాన్‌లోని ‘అజ్మీర్’లో ఉన్నది.

→ నిజాముద్దీన్ ఔలియా చిస్తీ సాధువులలో అత్యంత ప్రసిద్ధి గాంచినవాడు.

→ గోదాదేవి తిరుప్పావైని రచించెను.

→ వహదాత్-ఉల్-ఉజూద్ అనగా ఏకేశ్వరోపాసనని సూఫీతత్వం విశ్వసిస్తుంది.

→ జీవుడు దేవుడిలోని అంశ అని విశిష్టాద్వైతం చెప్పింది.

→ భక్తి : భక్తి అనగా దేవుని యందు ప్రేమ.

→ సగుణ భక్తి : భగవంతుని ఒక ఆకారంలో పూజించడం.

→ నిర్గుణ భక్తి : భగవంతుని నిరాకారంగా పూజించడం.

→ ద్వైత సిద్ధాంతం : ద్వైతమనగా రెండు. బ్రహ్మ మరియు ఆత్మ. రెండూ వేర్వేరు అంశాలని చెప్పే సిద్ధాంతం. జీవుడు వేరు మరియు దేవుడు వేరు.

→ అద్వైత సిద్ధాంతం : అంతా ఒక్కటే “బ్రహ్మం’ అని చెప్పే సిద్ధాంతం. బ్రహ్మం ఒక్కటే అంతా నిండి వుంది. జీవుడే దేవుడు.

→ విశిష్టాద్వైత సిద్ధాంతం : జీవుడు దేవుడిలోని అంశ.

→ బ్రహ్మ సూత్రాలు : వ్యాసుడు లేదా బాదరాయణుడు రచించాడు. బ్రహ్మ సూత్రాలనే వేదాంత సూత్రం అని కూడా అంటారు.

→ వచనములు : బసవేశ్వరుని రచనలను వచనములంటారు.

→ మఠములు : సన్యాస జీవితం గడుపు సాధువులుండు నివాసాలు.

→ గురు గ్రాంథ్ సాహెబ్ : సిక్కుల పవిత్ర గ్రంథం. దీనిని గురునానక్ రచించారు.

→ సూఫీ ఉద్యమం : ఇస్లాం మతంలోని సాంఘిక, మత సంస్కరణోద్యమం.

→ సూఫీ : సూఫీ పదం సాఫ్ అనే అరబిక్ పదం నుంచి గ్రహించబడింది. దీని అర్థం స్వచ్ఛత లేదా శుభ్రత.

→ సౌభ్రాతృత్వం : ప్రజలందరి మధ్య ‘సోదర భావం’.

→ ఉపనిషత్తులు : వీటికి వేదాంతాలు అని పేరు. ఇవి వేదాలలో చివరి భాగాలుగా చెప్పబడినవి.

→ నిగూఢార్థం : ప్రత్యేక ఆసక్తి లేదా జ్ఞానంతో కొందరు సాధకులు తెలుసుకున్న తత్వజ్ఞానం.

→ సమతా వాదం : అందరూ సమానమేనన్న ఆలోచనా విధానం.

→ పరవశం : వ్యక్తి తనను తాను మరచిపోయే భావాతీత స్థితి.

→ మోక్షం : భౌతిక విషయాలకు అతీతమైన చైతన్యాన్ని పొంది ఆత్మ భగవత్ సాన్నిధ్యాన్ని చేరడం.

1.

2.

3.

4.

Students can go through AP Board 7th Class Social Notes 7th Lesson మొఘల్ సామ్రాజ్యం to understand and remember the concept easily.

AP Board 7th Class Social Notes 7th Lesson మొఘల్ సామ్రాజ్యం

→ ఢిల్లీ సుల్తానులలో చివరి పాలకుడైన ఇబ్రహీం లోడీని క్రీ.శ. 1526లో పానిపట్టు యుద్ధంలో ఓడించి బాబర్ మొఘల్ సామ్రాజ్యాన్ని స్థాపించాడు.

→ క్రీ.శ. 1530లో బాబర్ మరణించెను.

→ మొఘల్ అనే పదం ‘మంగోల్’ అనే పదం నుంచి వచ్చింది.

→ బాబర్ తరువాత అతని కుమారుడు హుమాయూన్ సింహాసనానికి వచ్చెను.

→ షేర్షా క్రీ.శ. 1539లో చౌసా యుద్ధంలో మరియు క్రీ.శ. 1540లో జరిగిన కనౌజ్ యుద్ధంలో హుమాయూనన్ను ఓడించి ఇరాను తరిమివేసెను.

→ క్రీ. శ. 1555లో హుమాయూన్ తిరిగి ఢిల్లీని ఆక్రమించుకొనెను. క్రీ. శ. 1556లో మరణించెను.

→ షేర్షా సూర్ ఒక ఆప్షన్ నాయకుడు.

→ షేర్షా ఢిల్లీలో సూర్ రాజవంశాన్ని స్థాపించాడు.

→ షేర్షా తన సామ్రాజ్యాన్ని కాబూల్ నుండి బెంగాల్ మరియు మాళ్వా వరకు విస్తరించాడు.

→ అక్బర్ సంరక్షకుడు బైరాం ఖాన్.

→ క్రీ. శ. 1556లో రెండవ పానిపట్టు యుద్ధంలో అక్బర్, హేముని ఓడించినాడు.

→ మేవాడ్ పాలకుడైన మహారాణా ప్రతాప్, అక్బతో జీవితాంతం పోరాటం చేసాడు.

→ బీర్బల్, అక్బర్ సన్నిహితుడు. గొప్ప గాయకుడు మరియు కవి.

→ అహ్మద్ నగర్ రాణి అయిన చాంద్ బీబీ అక్బర్ అధికారాన్ని వ్యతిరేకించిన మహిళ.

→ జహంగీర్ అసలు పేరు ‘సలీమ్’.

→ షాజహాన్ జహంగీర్ కుమారుడు.

→ ఔరంగజేబు కాలంలో గురుతేజ్ బహదూర్, గురుగోవింద్ సింగ్ మరియు శివాజీ మొదలగువారు తిరుగుబాట్లు చేశారు.

→ ఔరంగజేబు క్రీ. శ. 1685లో బీజాపూర్, క్రీ.శ. 1687లో గోల్కొండను జయించాడు.

→ మొఘల్లది కేంద్రీకృత పరిపాలన, చక్రవర్తికే అన్ని అధికారాలు ఉండేవి.

→ అక్బర్ తన సామ్రాజ్యాన్ని అనేక సుబాలుగా విభజించి ప్రతి సుబాకు ఒక ‘సుబేదార్’ను నియమించాడు.

→ అక్బర్ తన రాజ్యా న్ని ’15’ సుబాలుగా విభజించాడు.

→ సుబాలను ‘సర్కారులుగా’, సర్కారులను ‘పరగణాలుగా విభజించాడు.

→ అక్బరు భూమిని సర్వే చేయించి, పండించిన పంట ప్రకారం పన్ను నిర్ణయించే వ్యవసాయ పద్ధతిని ప్రవేశపెట్టాడు.

→ భూమిని నాలుగు రకాలుగా విభజించి 1/3వ వంతు పంటను పన్నుగా వసూలు చేశారు.

→ అక్బర్ పాలనలో షేర్షా పరిపాలనా ముద్ర కొంత వరకు ప్రస్ఫుటమవుతుంది.

→ సైనిక విధానంలో అక్బర్ మన్సబ్ దారీ వ్యవస్థను ప్రవేశపెట్టాడు.

→ మన్నబ్ అంటే హోదా లేదా ర్యాంక్. ఇది 1) ర్యాంక్, 2) జీతాలు, 3) సైనిక బాధ్యతలు నిర్ధారించడానికి ఉపయోగించిన గ్రేడింగ్ పద్ధతి.

→ రాజపుత్రులలో ‘శిశోడియా’ వంశస్తులు మొఘలుల అధికారాన్ని అంగీకరించలేదు.

→ ఔరంగజేబు మరణానంతరము సామ్రాజ్యము విచ్ఛిన్నమైంది.

→ మొఘలులు సున్ని మతస్తులు. అక్బర్ మత సహనాన్ని పాటించాడు.

→ జిజియా పన్ను మరియు యాత్రికుల పన్నులను అక్బర్ రద్దు చేసాడు.

→ జిజియా పన్ను మరియు యాత్రికులపై పన్నులను ఔరంగజేబు తిరిగి విధించాడు.

→ ఔరంగజేబు ప్రజల నైతిక జీవనాన్ని పరిశీలించడానికి ‘ముతావాసిబ్’ అనే మతాధికారులను నియమించాడు.

→ అక్బర్ క్రీ. శ. 1575లో ఫతేపూర్ సిక్రీ వద్ద ‘ఇబాదత్ ఖానా’ అనే ప్రార్ధనా మందిరాన్ని నిర్మించాడు.

→ 1582 లో దీన్-ఇ-ఇలాహి అనే నూతన మతాన్ని అక్బర్ ప్రకటించాడు.

→ దీన్-ఇ-ఇలాహి అంటే ‘అందరితో శాంతి’ లేదా ‘విశ్వజనీన శాంతి’,

→ దీన్-ఇ-ఇలాహి మతంలో ’18’ మంది మాత్రమే చేరారు.

→ మొఘలులచే నియమించబడిన ప్రజాపనుల విభాగం సామ్రాజ్యంలో విస్తృతమైన రహదారి వ్యవస్థను రూపొందించింది.

→ వ్యవసాయ పన్ను ద్వారా వచ్చే ఆదాయం ముఖ్యమైన ఆదాయ వనరుగా ఉండేది.

→ షేర్షా సూర్ పాలనలో ప్రవేశపెట్టిన రూపాయి (వెండి నాణెం) మరియు దామ్ (రాగి నాణెం)లను మొఘలులు కొనసాగించారు.

→ మొఘల్ వ్యవస్థలో చెప్పుకోదగినది అక్బర్ కాలం నాటి రెవెన్యూ పాలన ‘జల్ట్’.

→ 1/3వ వంతు నుండి సగం వరకు భూమిశిస్తుగా నిర్ణయించారు.

→ అక్బర్ తన మత గురువు షేక్ సలీం ‘చిస్తి’ గౌరవార్థం రాజధానిని ఆగ్రా నుండి సిక్రీకి మార్చాలనుకున్నాడు.

→ ‘ఫతే’ అనగా విజయం

→ అక్బర్ ‘ఫతేబాద్’ అనే నగరాన్ని నిర్మించాడు. ఇదే ‘ఫతేపూర్ సిక్రి’.

→ అక్బర్ గుజరాత్ విజయాలకు జ్ఞాపకార్థంగా బులంద్ దర్వాజాను నిర్మించాడు.

→ ఎర్రకోట షాజహాన్ కాలం నాటి మొఘలుల సృజనాత్మక శైలికి తార్కాణం.

→ షాజహాన్ తన భార్య అయిన ముంతాజ్ ప్రేమకు గుర్తుగా తాజ్ మహల్ నిర్మించాడు.

→ ఖురాన్, ఫత్వా-ఇ-ఆలంగిరి మొదలైన ఇస్లామిక్ చట్టాలను స్వదేశీ భాషలలో బోధించటానికి ‘మక్తాబ్’ పాఠశాలలను నిర్మించారు మొఘలులు.

→ పర్షియన్ భాష అధికార భాషగా చలామణి అయినది.

→ బాబర్ ‘బాబర్ నామా’ను రచించాడు.

→ అబుల్ ఫజల్ ‘అయిన్-ఇ-అక్బరీ’, ‘అక్బర్ నామా’ అనే గ్రంథాలను రచించాడు.

→ తుజుక్-ఇ-జహంగీరీ అనే గ్రంథం జహంగీర్ ఆత్మకథ.

→ ప్రముఖ హిందీ కవి తులసీదాస్ రామాయణాన్ని ‘రామచరిత మానస్’ అనే పేరుతో హిందీలో రచించాడు.

→ మొఘలుల కాలంలో మినియేచర్ చిత్రకళ ప్రారంభమైంది.

→ అక్బర్ ఆస్థానంలో ‘తాన్ సేన్’ అనే సంగీత కళాకారుడు కలడు.

→ అక్బర్ ఆస్థానంలో 36 మంది సంగీతకారులు ఉన్నట్లు అబుల్ ఫజల్ పేర్కొన్నాడు.

→ మొఘల్ సామ్రాజ్యం క్రీ. శ. 1857లో బహదూర్ షా-II కాలంలో పతనమైంది.

→ జహంగీర్ పోషణలో చిత్రకళ అత్యున్నత స్థాయికి చేరుకుంది.

→ మరాఠా రాజ్య స్థాపకుడు. ‘శివాజీ’.

→ శివాజీ పూనే సమీపంలో శివనేరి కోటలో జన్మించాడు.

→ శివాజీ తండ్రి షాజీ భోంస్లే, తల్లి జిజియా బాయి.

→ శివాజీ సమర్థ రామదాస్ మరియు ఇతర మహారాష్ట్ర సాధువుల బోధనలచే ప్రభావితుడైనాడు.

→ శివాజీ దాదాజీ కొండదేవ్, తానాజీ మాల్ సురే వద్ద యుద్ధ విద్యలనభ్యసించాడు.

→ శివాజీ తన 19వ ఏట బీజాపూర్ సుల్తాన్ మహ్మద్ ఆదిల్ షా మరణానంతరం తోరణదుర్గంను జయించాడు.

→ బీజాపూర్ సుల్తాన్ శివాజీని అణచివేయడానికి తన సేనాధిపతి అఫలాఖానను పంపించాడు. కాని శివాజీ అతనిని సంహరించాడు.

→ ఔరంగజేబు శివాజీని, అణచడానికి తన సేనాని షయిస్తఖానను దక్కను పంపించాడు. కాని శివాజీ ఇతనిని కూడా ఓడించాడు.

→ ఔరంగజేబు తర్వాత రాజా జైసింగ్ నాయకత్వంలో పెద్ద సైన్యాన్ని శివాజీ పైకి పంపగా, శివాజీ ఓడింపబడ్డాడు.

→ రాయగఢ్ లో శివాజీకి ‘ఛత్రపతి’ బిరుదు ఇవ్వబడింది.

→ శివాజీకి పరిపాలనలో అష్టప్రధానులు అనే మంత్రులు సహాయపడ్డారు.

→ అష్టప్రధానులలో ప్రధానమంత్రిని ‘పీష్వా’ అని పిలిచేవారు.

→ శివాజీ మరణానంతరం ఏర్పడిన సంక్షోభంను పీష్వాలు విజయవంతంగా అధిగమించారు.

→ సుబాలు : మొఘల్ సామ్రాజ్యంలోని విభాగాలు (రాష్ట్రాలు).

→ సుబేదార్ : ‘సుబాకు’ అధికారి.

→ సర్కారులు : సుబా యొక్క భాగాలు (జిల్లాలు).

→ పరగణాలు : సర్కారు యొక్క భాగాలు (మండలాలు / తాలూకాలు)

→ రూపాయి : వెండి నాణెం

→ దామ్ : రాగి నాణెం

→ మన్సబ్దార్ : సైనిక హోదా (ర్యాంక్) కలిగి అక్బర్ పరిపాలన బాధ్యతను పంచుకునే అధికారులు.

→ సున్నీ మతం : ఇస్లాంలోని ఒక సంప్రదాయ మతం.

→ జిజియా పన్ను : ముస్లిం పాలనలో హిందువులు’ చెల్లించే పన్ను.

→ ముతావాసిబ్ : ప్రజల నైతిక జీవనాన్ని పరిశీలించడానికి ఔరంగజేబు నియమించిన మత అధికారులు.

→ దీన్-ఇ-ఇలాహి : “అందరితో శాంతి” లేదా “విశ్వజనీన శాంతి”, అక్బర్ ప్రకటించిన నూతన మతము.

→ జబ్త్ : అక్బర్ కాలంలో తోడర్మల్ ప్రవేశపెట్టిన రెవెన్యూ విధానము.

→ ఫతే : ఫతే అనగా విజయం.

→ బులంద్ దర్వాజ : గుజరాత్ విజయాలకు జ్ఞాపకార్థంగా అక్బర్ నిర్మించిన కట్టడము.

→ తాజ్ మహల్ : షాజహాన్ తన భార్య జ్ఞాపకార్థం పాలరాతితో కట్టించిన సమాధి.

→ ఖురాన్ : ఇస్లాంల పవిత్ర గ్రంథము.

→ మక్తాబ్ : ఖురాన్, ఇస్లామిక్ చట్టాలను బోధించే పాఠశాల.

→ నవరత్నాలు : అక్బర్ ఆస్థానంలోని (కవులు) కళాకారులు తొమ్మిది మందిని నవరత్నాలు అంటారు.

→ ఛత్రపతి : శివాజి (మహరాజ్)కి రాయగఢ్ లో ఇవ్వబడిన బిరుదు.

→ పీష్వా : శివాజి పరిపాలనలో ప్రధాన మంత్రిని పీష్వా అంటారు.

→ అష్ట ప్రధానులు : శివాజి పాలనలో సహాయపడే ఎనిమిది మంది మంత్రులు (అధికారులు).

→ రాజపుత్రులు : ఉత్తర భారతదేశంలో ధైర్యసాహసాలు కలిగిన శక్తివంతమైన రాజవంశములు.

→ పోరాట యోధుడు : ధైర్యుడైన లేదా అనుభవజ్ఞుడైన సైనికుడు లేదా పోరాట యోధుడు.

→ రీజెంట్ : ఒక చక్రవర్తి మైనర్ లేదా అసమర్ధుడు అయినప్పుడు ఒక రాష్ట్రాన్ని పరిపాలించడానికి నియమించబడిన వ్యక్తి.

→ మత విశ్వాసి : మత విశ్వాసాన్ని విశ్వసించే లేదా ఆచరించే వ్యక్తి.

→ గెరిల్లా యుద్ధం : కొంత మంది సైనికుల ఆకస్మిక దాడి, ఒక యుద్ధ వ్యూహం.

→ వ్యవసాయిక : వ్యవసాయ భూముల యాజమాన్యం మరియు వాడకానికి సంబంధించినది.

1.

3.

4.

Students can go through AP Board 7th Class Social Notes 6th Lesson విజయనగర సామ్రాజ్యం to understand and remember the concept easily.

AP Board 7th Class Social Notes 6th Lesson విజయనగర సామ్రాజ్యం

→ విజయనగర సామ్రాజ్యం క్రీ.శ. 1336 నుండి క్రీ.శ. 1646 వరకు 200 సంవత్సరాలకు పైగా భారతదేశ చరిత్రలో గొప్ప స్థానాన్ని ఆక్రమించింది.

→ 14, 16 శతాబ్దాలలో మొత్తం దక్షిణ భారతదేశంలో విస్తరించిన, ప్రపంచంలో రెండవ అతి పెద్ద రాజధాని నగరం కల సామ్రాజ్యపు రాజధాని.

→ లండన్, పారిస్ కంటే పెద్దదిగా పేరుగాంచింది. విజయనగర సామ్రాజ్యానికి ‘హంపి’ రాజధానిగా ఉండేది.

→ విజయనగరం ఆ కాలంలో ప్రపంచంలోనే అత్యంత ధనిక రాజ్యం.

→ క్రీ.శ. 1336లో సంగమ వంశానికి చెందిన మొదటి హరిహర రాయలు మొదటి బుక్క రాయలు చేత విద్యారణ్య స్వామి వారి ప్రోత్సాహముతో విజయనగర సామ్రాజ్యం స్థాపించబడింది.

→ మొదటి హరిహర, బుక్కరాయలు మొదటగా వరంగల్లుకు చెందిన కాకతీయ రాజు రెండవ ప్రతాపరుద్రుని ఆస్థానంలో క్రీ.శ. 1323లో పని చేశారు.

→ క్రీ.శ. 1336లో విజయనగరము అనే కొత్త నగరాన్ని ‘తుంగభద్ర’ నదికి దక్షిణ ఒడ్డున స్థాపించారు.

→ హంపి వద్ద ఉన్న శిథిలాలు 1805లో ఇంజనీర్, పూరాతత్వవేత్త అయిన కల్నల్ కొలిన్ మెకంజీ కాలంలో వెలుగులోకి వచ్చాయి.

→ సంగమ రాజవంశంలో గొప్ప పాలకుడు ‘రెండవ దేవరాయలు’.

→ రెండవ దేవరాయలను ప్రౌఢ దేవరాయలు అని కూడా అంటారు.

→ రెండవ దేవరాయలు కళింగ సైన్యాన్ని ఓడించాడు. కొండవీడును స్వాధీనం చేసుకుని రాజమండ్రి వరకు తన అధికారాన్ని సుస్థిరం చేశాడు.

→ సంగమ రాజవంశం తరువాతి రెండవ రాజవంశం సాళువ రాజవంశం.

→ సాళువ వంశం సాళువ నరసింహరాయలచే స్థాపించబడింది.

→ తుళువ రాజవంశం విజయనగర సామ్రాజ్యంలోని మూడవ రాజవంశం.

→ శ్రీకృష్ణ దేవరాయలు విజయ నగరాన్ని పాలించిన పాలకులలో చాలా శక్తివంతమైన పాలకుడు.

→ తుళువ వంశ స్థాపకుడు వీర నరసింహరాయలు.

→ శ్రీకృష్ణ దేవరాయలు తుళువ వంశానికి చెందినవాడు.

→ శ్రీకృష్ణ దేవరాయలు విదేశీ వాణిజ్యం యొక్క ప్రాధాన్యతను అర్థం చేసుకుని ఓడల ద్వారా వ్యాపారాన్ని అభివృద్ధి చేసాడు.

→ ‘దివానీ’ యుద్ధంలో ముస్లిం సైన్యాలు శ్రీకృష్ణదేవరాయల చేత నిర్ణయాత్మకంగా ఓడించబడ్డాయి.

→ క్రీ.శ. 1520లో ఆదిల్ షాను ఓడించి రాయచూర్ నగరాన్ని స్వాధీనం చేసుకున్నాడు.

→ శ్రీకృష్ణ దేవరాయలు పోర్చుగీసు మరియు అరబ్ వ్యాపారులతో స్నేహపూర్వక సంబంధాలు కొనసాగించాడు.

→ సాహిత్యం, కళలను గొప్పగా పోషించి, శ్రీకృష్ణదేవరాయలు ‘ఆంధ్ర భోజుడు’ అని పిలువబడ్డాడు.

→ “దేశ భాషలందు తెలుగు లెస్స” అని శ్రీకృష్ణదేవరాయలు పలికాడు.

→ అష్ట దిగ్గజములు అని పిలువబడే ఎనిమిది మంది ప్రముఖ పండితులు శ్రీకృష్ణదేవరాయల ఆస్థానంలో ఉండేవారు.

→ ‘ఆంధ్ర కవితా పితామహుడు’ అని అల్లసాని పెద్దనను పిలిచేవారు. అతని రచనల్లో ‘మను చరిత్ర’, ‘హరికథాసారం’ ముఖ్యమైనవి.

→ శ్రీకృష్ణ దేవరాయలు స్వయంగా కవి. తెలుగులో ‘ఆముక్త మాల్యద’ సంస్కృతంలో జాంబవతి కళ్యాణం, ఉషా పరిణయం ఈయన ముఖ్యమైన రచనలు.

→ విజయనగరంలో విఠలస్వామి, హజారా రామస్వామి ఆలయాలను కూడా శ్రీకృష్ణదేవరాయలు నిర్మించాడు.

→ విజయనగరంలో తన తల్లి నాగలాంబ జ్ఞాపకార్థం నాగలాపురం అనే కొత్త నగరాన్ని కూడా నిర్మించాడు.

→ విజయనగర సామ్రాజ్యం యొక్క నాల్గవ మరియు చివరి రాజవంశం అరవీడు / అరవీటి రాజవంశం.

→ తళ్ళికోట యుద్ధం తర్వాత విజయనగర సామ్రాజ్యం క్షీణించింది.

→ విజయనగర రాజుల పాలనలో రాజు సంపూర్ణ అధికారాన్ని కల్గి ఉండేవాడు.

→ ఈ సామ్రాజ్యాన్ని మండలాలు, నాడులు, స్థలాలు, గ్రామాలుగా విభజించారు.

→ మండల పాలకుని ‘మండలేశ్వరుడు’ లేదా ‘నాయక్’ అని పిలిచేవారు.

→ సాధారణంగా ఉత్పత్తిలో 1/6 (ఆరవ వంతు) వ భూమి శిస్తుగా నిర్ణయించారు.

→ సైన్యంలోని ఉన్నత స్థాయి అధికారులను నాయకులు లేదా పాలిగార్లు అని పిలిచేవారు.

→ పాలిగార్ల సేవలకు బదులుగా వారికి భూమి మంజూరు చేయబడింది. ఈ భూములను ‘అమరం’ అని పిలిచేవారు.

→ విజయనగర సామ్రాజ్యంలో కోటలను, సాయుధ దళాలను నియంత్రించే సైనిక అధికారులను అమర నాయకులు అంటారు.

→ సైనికుల జీతాలు సాధారణంగా నగదు రూపంలో చెల్లించేవారు.

→ వీరు యుద్ధంలో విష వాయువులను గుర్తించడానికి “పక్షులను” ఉపయోగించేవారు.

→ కుమార కంపన భార్య గంగాదేవి ‘మధురా విజయం’ అనే ప్రసిద్ధ రచన చేసింది.

→ వ్యవసాయం ప్రజల ప్రధాన వృత్తిగా కొనసాగింది.

→ “వరాహ” అనునది ప్రధాన బంగారు నాణెం.

→ మలబార్ తీరంలో అనేక నౌకాశ్రయాలు ఉండేవి. వాటిలో ప్రధానమైనది ‘కన్ననూర్’.

→ పశ్చిమాన అరేబియా, పర్షియా, దక్షిణాఫ్రికా మరియు పోర్చుగల్ మరియు తూర్పున బర్మా, మలయా ద్వీపకల్పం మరియు చైనాతో వాణిజ్య సంబంధాలు వృద్ధి చెందాయి.

→ పత్తి, పట్టు, సుగంధ ద్రవ్యాలు, బియ్యం, ఇనుము, సురేకారం మరియు చక్కెర ఎగుమతులలో ప్రధాన వస్తువులు.

→ గుర్రాలు, ముత్యాలు, రాగి, పగడము, పాదరసం, చైనా పట్టు మరియు వెల్వెట్ వస్త్రాలను దిగుమతి చేసుకొన్నారు.

→ ఓడల నిర్మాణ కళ అభివృద్ధి చెందింది.

→ శ్రీకృష్ణ దేవరాయలు కాలంలో పోర్చుగీసు యాత్రికులైన డువార్టే బార్బోసా మరియు డొమింగో పేర్లు విజయనగరాన్ని సందర్శించారు.

→ దేవరాయ-II కాలంలో ఇటాలియన్ యాత్రికుడు నికోలో కాంటి మరియు పర్షియన్ యాత్రికుడు అబ్దుల్ రజాట్లు విజయనగర సామ్రాజ్యాన్ని సందర్శించారు.

→ విఠల స్వామి దేవాలయము, హజారా రామాలయం దేవాలయాలు కాంచీపురంలోని వరద రాజ దేవాలయము మరియు ఏకాంబర నాథ దేవాలయాలు విజయనగర రాజుల నిర్మాణ శైలి గొప్పతనానికి ఉదాహరణలుగా నిలుస్తాయి.

→ తిరుపతిలో శ్రీకృష్ణదేవరాయలు మరియు అతని రాణుల యొక్క లోహ చిత్రాలు లోహాల పనితనానికి ఉదాహరణలు.

→ ఈ కాలంలో కర్ణాటక సంగీత సాంప్రదాయం అభివృద్ధి చెందింది.

→ విద్యారణ్య స్వామి ‘సంగీత సర్వస్వం’ అనే గ్రంథాన్ని రాశారు.

→ ప్రౌఢ దేవరాయలు రాసిన ‘మహానాటక సుధానిధి’ అను రచన కూడా సంగీతానికి చెందినదే.

→ కర్ణాటక సంగీత త్రయం దీక్షితార్, శ్యామశాస్త్రి మరియు త్యాగరాజ స్వామి తంజావూరు ఆస్థానానికి చెందినవారు.

→ భరతనాట్యం భరత ముని చేత పరిచయం చేయబడింది.

→ సిద్ధేంద్ర యోగి ప్రవేశపెట్టిన ‘కూచిపూడి’, ‘పేరిణి’ నాట్యం కూడా ఈ కాలంలో ప్రాచుర్యం పొందాయి.

→ భాగవతం నుండి ప్రత్యేకంగా ఉద్భవించిన ఇతివృత్తాలతో ‘యక్షగానమనే’ నృత్య రూపకం కూడా ప్రజాధరణ పొందింది.

→ ఆళియరామ రాయలు పాలనలో మహ్మదీయ సంయుక్త దళాలు కూటమిగా ఏర్పడి క్రీ.శ. 1565లో ‘తళ్ళికోట’ వద్ద అతనిని ఓడించాయి.

→ తళ్ళికోట యుద్ధాన్నే రాక్షస తంగడి యుద్ధం అని కూడా అంటారు.

→ విజయనగర రాజ్యానికి చివరి పాలకుడు మూడవ శ్రీరంగ రాయలు.

→ రెడ్డి రాజులు క్రీ.శ. 1325 నుండి 1448 వరకు వంద సంవత్సరాల పాటు తీరప్రాంతంతో పాటు మధ్య ఆంధ్రాను పాలించారు.

→ వీరి మొదటి రాజధాని “అద్దంకి’, తరువాత దానిని ‘కొండవీడు’కు మార్చారు.

→ ఆంధ్ర మహాభారతమును రచించిన కవిత్రయములో ఒకరైన ‘ఎర్రాప్రగడ’ ప్రోలయ వేమారెడ్డి ఆస్థాన కవిగా ఉండేవాడు. ఆయనకు ప్రబంధ పరమేశ్వరుడు అనే బిరుదు ఉంది.

→ అల్లావుద్దీన్ బహ్మన్‌షా క్రీ.శ. 1347లో బహమనీ రాజ్యాన్ని స్థాపించాడు.

→ అల్లావుద్దీన్ బహ్మను హసన్ గంగూ అని కూడా పిలుస్తారు. ఇతని రాజధాని ‘గుల్బర్గా’.

→ అహ్మదాలిషా రాజధానిని గుల్బర్గా నుండి ‘బీదర్’కు మార్చాడు.

→ మూడవ మహ్మద్ షా విజయానికి కారణం ఆయన మంత్రి మహమూద్ గవాన్ సేవలు, సలహాలు.

→ మహమూద్ గవాన్ పర్షియన్ వ్యాపారి.

→ మూడవ మహమ్మద్ షా క్రీ.శ. 1482లో మరణించాడు.

→ మూడవ మహమ్మద్ షా తర్వాత బహమనీ సామ్రాజ్యం అహ్మద్ నగర్, బీరార్, బీదర్, బీజాపూర్, గోల్కొండ అనే ఐదు భాగాలుగా విడిపోయింది.

→ దో ఆబ్ (అంతర్వేది) : రెండు నదుల మధ్య ప్రాంతం.

→ అష్ట దిగ్గజములు : శ్రీకృష్ణ దేవరాయల ఆస్థానమంధళి, ఎనిమిది మంది కవులు / పండితులు.

→ మండలేశ్వరుడు : మండల పాలకుడు.

→ అశ్విక దళం : గుర్రాలపై కూర్చొని యుద్ధం చేసే సైన్యంలోని ఒక దళం.

→ పాలిగార్లు : సైన్యంలోని ఉన్నత స్థాయి అధికారులు

→ అమరం : పాలిగార్ల సేవలకు బదులు మంజూరు చేయబడిన భూమి.

→ అమర నాయకులు : కోటలను, సాయుధ దళాలను నియంత్రించే సైనిక అధికారులు.

→ వరాహ : విజయనగర సామ్రాజ్యంలోని బంగారు నాణెం.

→ కన్ననూర్ : మలబార్ తీరంలోని ప్రధానమైన నౌకాశ్రయం.

→ రాయగోపురం : ఎత్తైన ఆలయ ముఖద్వారం.

→ కర్ణాటక సంగీత త్రయం : దీక్షితార్, శ్యామశాస్త్రి మరియు త్యాగరాజ స్వామి.

→ కస్టమ్ సుంకాలు : ఎగుమతులు, దిగుమతులపై పన్నులు.

→ నాడులు : మండలం యొక్క విభాగాలు (ప్రస్తుత జిల్లా స్థాయి)

→ అంతర్వేది : రెండు నదుల మధ్య ఉన్న భూభాగము.

→ ఫిరంగులు : యుద్ధాలలో ఉపయోగించే పెద్ద శక్తివంతమైన తుపాకులు.

→ నాయక : చక్రవర్తి తరపున పౌర మరియు సైనిక విధులను నిర్వర్తించేవారు.

→ వ్యాపారులు : అమ్మకము మరియు కొనుగోళ్ళు చేసేవారు.

→ దండయాత్ర : సాయుధ దళాల దాడి, ఆక్రమణ లేదా ముట్టడి.

1.

2.

3.

4.

Students can go through AP Board 7th Class Social Notes 5th Lesson కాకతీయ రాజ్యం to understand and remember the concept easily.

AP Board 7th Class Social Notes 5th Lesson కాకతీయ రాజ్యం

→ మధ్యయుగ కాలంలో దక్షిణ భారతదేశంలో ఐదు ముఖ్యమైన రాజ్యాలు ఆవిర్భవించాయి. అవి :

→ కల్యాణి చాళుక్యులు, యాదవులు, కాకతీయులు, హోయసల మరియు పాండ్య రాజ్యాలు.

→ కల్యాణి చాళుక్య వంశ స్థాపకుడు రెండవ తైలపుడు. వీరి రాజధాని బీదర్ జిల్లాలో గల బసవ కళ్యాణి.

→ వీరు సంస్కృత, కన్నడ భాషలను ప్రోత్సహించారు.

→ బిల్హణుడు విక్రమాంకదేవ చరిత్రను రాశాడు.

→ రన్నడు అను ప్రసిద్ధ కన్నడ కవి వీరి ఆస్థానానికి చెందినవాడు.

→ కల్యాణి చాళుక్యులు ఘటికులు అనే విద్యా సంస్థలను స్థాపించారు.

→ యాదవులు మొదట కళ్యాణి చాళుక్యుల సామంతులుగా పనిచేశారు.

→ యాదవుల రాజధాని దేవగిరి.

→ బిల్లమ యాదవ రాజవంశం స్థాపకుడు.

→ సింఘన యాదవ రాజులలో సుప్రసిద్ధుడు.

→ హోయసాలుల ద్వారా సముద్రంనకు చెందినవారు.

→ బిత్తుగ విష్ణువర్ధన కాలంలో వీరు ప్రాముఖ్యత పొందారు.

→ ద్వైత సిద్ధాంతం – మధ్వాచార్యులు, విశిష్టాద్వైతము – రామానుజాచార్యులు అనుసరించారు.

→ పాండ్యులు ‘మదురై’ ను రాజధానిగా చేసుకుని పాలించారు.

→ పాండ్య రాజైన కులశేఖరుడు శ్రీలంక వరకు విజయవంతమైన దండయాత్రను పూర్తి చేసాడు.

→ మార్కోపోలో అను వెన్నీసు యాత్రికుడు కులశేఖరుని పాలనా కాలములో సందర్శించి అతని పాలనను ప్రశంసించాడు.

→ కాకతీయులు మొదట్లో రాష్ట్రకూటులు మరియు పశ్చిమ చాళుక్యులకు సామంతులుగా పనిచేశారు.

→ ‘కాకతి’ అనే దేవతను ఆరాధించిన కారణంగా వీరికి కాకతీయులు అను పేరు వచ్చింది.

→ ‘కాకతి’ దుర్గా దేవి యొక్క మరొక రూపం.

→ కాకతీయ రాజవంశం ‘గుంద్యెన’ చేత స్థాపించబడింది.

→ కాకతీయులు తమ మొదటి రాజధానిగా ‘హనుమకొండ’ నుండి పాలన ప్రారంభించారు.

→ కాకతీయ రాజు రుద్రదేవుడు కొత్త రాజధాని ఓరుగల్లును నిర్మించటముతో తమ రాజధానిని హనుమకొండ నుండి ఓరుగల్లుకు మార్చారు.

→ వీరిని ఆంధ్ర రాజులు అని కూడా పిలుస్తారు.

→ మొదటి తెలుగు గ్రంథముగా పిలువబడుతున్న ‘శ్రీమదాంధ్ర మహాభారతం’ రచించిన ‘తిక్కన’ ఈ కాలమునకు చెందినవాడు.

→ కాళేశ్వరము (తెలంగాణ), శ్రీశైలము (రాయలసీమ), ద్రాక్షారామం (తీర ఆంధ్ర ప్రాంతము)లను కలిపి త్రిలింగ దేశం అంటారు.

→ ఓరుగల్లు ప్రస్తుత పేరు వరంగల్, ప్రాచీన నామం – ఏకశిలా నగరం.

→ రెండవ ప్రోలరాజు (క్రీ.శ. 1116-1157) పాలన కాకతీయ చరిత్రలో ముఖ్యమైన మైలురాయి.

→ రుద్రదేవుని (క్రీ.శ. 1158-1195) విజయాలు హనుమకొండ శాసనంలో వివరించబడ్డాయి.

→ రుద్రదేవుడు సంస్కృత భాషలో ‘నీతి సారము’ అనే గ్రంథం రాశాడు.

→ రుద్రదేవుడు హనుమకొండలో వెయ్యి స్తంభాల గుడిని నిర్మించాడు.

→ రుద్రదేవుడు స్థాపించిన ఓరుగల్లు అతని వారసులకు రాజధానిగా మారింది.

→ గణపతి దేవుడు (క్రీ.శ. 1199-1162)కు “మహా మండలేశ్వర” అనే బిరుదు కలదు.

→ కాకతీయ పాలకులలో గణపతి దేవుడు అత్యంత శక్తివంతమైనవాడు.

→ గోదావరి ప్రాంతం నుండి మొదలుకొని చెంగల్పట్టు వరకు మరియు ఎలగందల నుండి సముద్రం వరకు తన సామ్రాజ్యాన్ని (గణపతి దేవుడు) నిర్మించాడు.

→ ‘మోటుపల్లి’ శాసనాన్ని గణపతి దేవుడు జారీ చేశాడు.

→ గణపతి దేవుడు ఓరుగల్లు కోట నిర్మాణమును పూర్తి చేసాడు.

→ ‘అన్నపక్షి’ అనే సంస్కృత పదం పౌరాణిక పక్షి హంసను సూచిస్తుంది.

→ హంస కాకతీయ కళాతోరణం పైన రెండు వైపులా ఉంచబడింది.

→ క్రీ.శ. 1262లో రుద్రమదేవి పాలన ప్రారంభమైంది.

→ రుద్రమదేవి ఆస్థానాన్ని సందర్శించిన ఇటాలియన్ యాత్రికుడు మార్కోపోలో ఆమె పరిపాలనా సామర్థ్యాన్ని ప్రశంసించినాడు.

→ ఆంధ్రప్రదేశ్ లోని పశ్చిమ గోదావరి జిల్లాలో ఉన్న నిడదవోలు పాలకుడు ‘చాళుక్య వీరభద్రుడు’ని వివాహం చేసుకుంది.

→ రుద్రమదేవి తన మనవడు ప్రతాపరుద్రుని తదుపరి వారసుడిగా ప్రకటించింది.

→ రుద్రమదేవికి గల ఇతర పేర్లు రుద్రమాంబ, రుద్రదేవ మహారాజు.

→ కాకతీయుల రాజ్యపాలన సైనిక ప్రాతిపదికగా నిర్వహించబడింది.

→ తమ రాజ్య భాగాలను చిన్న విభాగాలుగా విభజించి నాయంకరులు అనే సైనిక నాయకులను వాటి పరిపాలకులుగా నియమించారు.

→ ప్రతాపరుద్రుని కాలం నాటికి దాదాపు 172’ మంది నాయంకరులు వుండేవారు.

→ గ్రామ పరిపాలన విభాగాలను ‘స్థల’ మరియు ‘నాడు’ అనే రెండు ప్రధాన తరగతులుగా విభజించారు.

→ పది నుండి అరవై వరకు గ్రామాల సమూహాన్ని ‘స్థల’ అంటారు.

→ కొన్ని స్థలాల కలయికతో ఏర్పాటు చేయబడిన ప్రాంతాన్ని ‘నాడు’ అంటారు.

→ ‘ఆయగార్లు’ అని పిలువబడే గ్రామ అధికారులు గ్రామాల పాలనను పర్యవేక్షించేవారు.

→ గ్రామము ప్రాథమిక పరిపాలనా విభాగము.

→ గ్రామంలోని భూమి సంబంధ రికార్డులను పర్యవేక్షించే అధికారి ‘కరణం’.

→ గ్రామ రక్షక భటుడు ‘తలారి’.

→ రాజుకి చెందిన ప్రభుత్వ భూమిని ‘రాచ పొలం’ అంటారు.

→ నీటి వసతి గలిగిన భూమిని వెలిపొలం (వెలిచేను) అనేవారు.

→ వివిధ రకాల పండ్ల చెట్లతో కూడిన భూమి – తోట పొలం (తోట భూమి).

→ ప్రభుత్వ భూమిని కౌలు ప్రాతిపదికన సాగు చేసిన రైతులు ‘అర్ధశిరి’ అని పిలువబడ్డారు.

→ ‘ఇల్లరి’ అనేది కాకతీయుల నాటి గృహ పన్ను.

→ ‘పుల్లరి’ అనేది కాకతీయుల నాటి అటవీ ఉత్పత్తులపై పన్ను.

→ ‘అడ్డపట్టు సుంకం’ అనేది కాకతీయుల నాటి గొర్రెల మందపై విధించిన పన్ను.

→ పన్ను వసూలు కోసం కాకతీయులు ‘సుంకాధికారి’ అనే వారిని నియమించారు.

→ విదేశీ వాణిజ్యం అభివృద్ధి చేసే ఉద్దేశ్యంతో ‘మోటుపల్లి’ నౌకాశ్రయాన్ని అభివృద్ధి చేశారు.

→ నేరుగా చక్రవర్తికి చెల్లించవలసిన పన్నులు. దరిశనం, అప్పనం, ఉపకృతి అను పన్నులు.

→ కాకతీయుల కాలంలో శైవ మతం బాగా ప్రసిద్ది చెందింది.

→ మల్లికార్జున పండితారాధ్యుడు ‘శివతత్వసారము’ అనే గ్రంథాన్ని రచించాడు.

→ కాకతీయుల కాలంలో ‘పేరిణి’ ప్రసిద్ధ నాట్యం. పద్మశ్రీ నటరాజ రామకృష్ణ ఈ నృత్యంలో ప్రఖ్యాతిగాంచారు.

→ పాల్కురికి సోమనాథుడు ‘బసవ పురాణం’ అనే గ్రంథాన్ని రచించాడు.

→ నన్నెచోడుడు ‘కుమారసంభవం’ అనే గ్రంథాన్ని రచించాడు.

→ విద్యానాథుడు సంస్కృతంలో ‘ప్రతాపరుద్రీయము’ అనే గ్రంథాన్ని రచించాడు.

→ జయాపసేనాని సంస్కృతంలో ‘గీత రత్నావళి’ ‘నృత్య రత్నావళి’ అనే గ్రంథాలు రచించాడు.

→ వల్లభరాయుడు తెలుగులో ‘క్రీడాభిరామం’ అనే గ్రంథాన్ని రచించాడు.

→ వెయ్యి స్తంభాల ఆలయాన్ని ‘రుద్రేశ్వర’ ఆలయం అంటారు. ఇది హనుమకొండలో ఉంది.

→ వెయ్యి స్తంభాల ఆలయాన్ని రుద్రదేవుడు నిర్మించాడు. ‘ఏకశిలా’ నంది ఈ ఆలయ ప్రధాన ఆకర్షణ.

→ వరంగల్ ప్రాంతంలోని ‘పాలంపేట’ గ్రామానికి సమీపంలో రామప్ప ఆలయం కలదు.

→ రేచర్ల రుద్రుడు రామప్ప ఆలయాన్ని నిర్మించాడు.

→ ఈ ఆలయంలో విష్ణువు మరియు శివుడులను ఒకే చోట ఆరాధించటం ప్రసిద్ది.

→ ఈ ఆలయంలో నల్ల గ్రానైట్ రాయితో నిర్మించిన విగ్రహాలు కలవు.

→ స్తంభాల పైన చెక్కిన శిల్పాలతో మండప నిర్మాణము, అంతరాలయము మరియు గర్భగుడి నిర్మాణ నమూనాలను అనుసరించారు. ఈ శైలిని ‘త్రికూట పద్ధతి’ అని కూడా అంటారు.

→ క్రీ.శ. 1323లో ఉలుగ్ ఖాన్ నాయకత్వంలో ఢిల్లీ సుల్తానులు కాకతీయ రాజ్యాన్ని ఆక్రమించుకున్నారు. ప్రతాపరుద్రుని ఖైదు చేశారు.

→ ‘విలస’ శాసనము ఢిల్లీ సుల్తానులు, కాకతీయులపై చేసిన దండయాత్రల గురించి, ‘ముసునూరి నాయకుల’ గురించి తెల్పుతుంది.

→ ముసునూరి నాయకుల్లో ఒకరైన ప్రోలయ నాయకుడు ‘రేకపల్లె’ రాజధానిగా అధికారంలోకి వచ్చాడు.

→ ముసునూరి కాపయ నాయకుడు క్రీ.శ. 1336లో తుగ్లక్ పాలనను వరంగల్ నుండి తరిమికొట్టడానికి తిరుగుబాటును నడిపించాడు.

→ ఘటికలు : మధ్యయుగం నాటి విద్యా సంస్థలు / కళాశాలలు.

→ సామంతులు : చక్రవర్తికి కప్పం చెల్లించే రాజులు.

→ ద్వైతము : రెండుగా ఉన్నవి (ఆత్మ, పరమాత్మ).

→ అద్వైతము : ఒక్కటి మాతమ్రే (పరమాత్మ).

→ చరిత్రకారుడు : మానవులకి సంబంధించిన గడచిన సంఘటనల గురించి అధ్యయనం చేసి వ్రాసే వ్యక్తి.

→ పురావస్తు శాస్త్రవేత్త : పురాతన భవనాలు, అవశేషాలు, శిల్పం, శాసనాలు మరియు పురావస్తు త్రవ్వకాల గురించి అధ్యయనం చేసే వ్యక్తి.

→ కాకతీయులు : ‘కాకతి’ అనే దేవతను ఆరాధించిన వారు కాకతీయులు.

→ త్రిలింగ దేశం : కాళేశ్వరము (తెలంగాణ), శ్రీశైలము (రాయలసీమ), ద్రాక్షారామం (కోస్తా ఆంధ్రలను) కలిపి త్రిలింగ దేశం అంటారు.

→ దివిసీమ : కృష్ణానది బంగాళాఖాతంలో కలిసే ముందు రెండు పాయలుగా విడిపోతుంది. ఈ రెండు పాయల మధ్య ప్రాంతమే దివిసీమ.

→ అన్నపక్షి : పౌరాణిక పక్షి ‘హంస’

→ మార్కోపోలో : ఇటాలియన్ యాత్రికుడు రుద్రమదేవి ఆస్థానాన్ని సందర్శించాడు.

→ నాయంకరులు : కాకతీయుల చిన్న విభాగాలకు పరిపాలకులుగా నియమించబడిన సైనిక నాయకులు.

→ స్థల : పది నుండి అరవై వరకు గ్రామాల సమూహం.

→ నాడు : కొన్ని స్థలాల కలయికతో ఏర్పాటు చేయబడిన ప్రాంతం నాడు.

→ ఆయగార్లు : గ్రామ పాలనను పర్యవేక్షించే గ్రామ అధికారులు.

→ కరణం : గ్రామంలోని భూమి సంబంధ రికార్డులను పర్యవేక్షించే అధికారి.

→ రెడ్డి : గ్రామ పెద్ద.

→ తలారి : గ్రామ రక్షక భటుడు.

→ రాచపొలం : రాజుకి చెందిన ప్రభుత్వ భూమి.

→ వెలిపొలం (వెలిచేను) : నీటి వసతి గలిగిన భూమి.

→ తోట పొలం (తోట భూమి) : వివిధ రకాల పండ్ల చెట్లతో కూడిన భూమి.

→ ‘అర్ధశిరి’ : ప్రభుత్వ భూమిని కౌలు ప్రాతిపదికన సాగుచేసిన రైతులు.

→ ‘ఇల్లరి’ : గృహపన్ను.

→ పుల్లరి : అటవీ ఉత్పత్తులపై పన్ను.

→ అడ్డపట్టు సుంకం : గొర్రెల మందపై విధించిన పన్ను.

→ సుంకాధికారి : పన్నులు వసూలు చేయటం కోసం నియమించిన అధికారి.

→ పేరిణి నాట్యం : యుద్ధ సమయంలో ప్రదర్శించే కాకతీయుల నాటి ప్రసిద్ధ నాట్యం.

→ ఏకశిలా నంది : ఒకే రాయిపై చెక్కిన నంది విగ్రహము.

→ సప్త స్వరాలు : ఏడు స్వరములు (స,రి,గ,మ,ప,ద,ని).

→ విలాస శాసనము : ముసునూరి నాయకుల గూర్చి తెలుపు శాసనము.

→ ఇతిహాసాలు : రామాయణం, మహాభారతం భారతదేశ ఇతిహాసాలు.

→ త్రికూట పద్దతి : మండపము, అంతరాలయము మరియు గర్భగుడి ఇలాంటి మూడు నిర్మాణ నమూనాలతో నిర్మితమైన శైలిని త్రికూట పద్ధతి అంటారు.

→ వారసత్వం : పూర్వీకుల నుండి అందించబడినది.

→ రేకపల్లె : పాపికొండల సమీపంలో శబరి నది లోయలో కల్గిన ప్రాంతం.

→ సామంత ప్రభువులు : చక్రవర్తి ఆదేశాలు లేదా సూచనలను విధేయతతో అనుసరిస్తూ అతని అధీనంలో ఉన్నవారు.

→ పోషకులు : సంస్కృతిని మరియు వారసత్వంను పెంపొందించడానికి తమ సహాయాన్ని మద్దతును ఇచ్చిన పాలకులు.

→ వీర శైవం : హిందూ మతం నుండి మధ్య యుగములో నూతనముగా ఆవిర్భవించిన ఒక శాఖ.

→ శాసనం : లిఖించబడిన ఒక చారిత్రక సంఘటన లేదా ఆదేశము.

→ శోభ : ప్రకాశవంతమైన శిల్పకళా ప్రదర్శన.

→ రాజవంశం : ఒకే సంతతికి చెందిన పాలకులు వారసత్వ పాలన చేయుట.

→ సయోధ్య కుదరని సామంత ప్రభువులు : చక్రవర్తికి అవిధేయులుగా ఉన్నవారు.

→ శాంతి ఒప్పందము : యుద్ధము. ముగింపు తరువాత కొనసాగడానికి మరియు అనుసరించడానికి కుదుర్చుకున్న అంగీకారము.

→ వారసుడు : వంశ పారంపర్యంగా బాధ్యతలు చేపట్టే అర్హత కలిగిన వ్యక్తి.

→ తెగ : ఒక సాధారణ పూర్వీకుల నుండి వచ్చిన వారి సమూహం.

1.

2.

3.

4.

Students can go through AP Board 7th Class Social Notes 4th Lesson ఢిల్లీ సుల్తానులు to understand and remember the concept easily.

AP Board 7th Class Social Notes 4th Lesson ఢిల్లీ సుల్తానులు

→ క్రీ. శ. 13వ శతాబ్దము నుండి 16వ శతాబ్దం వరకు ఢిల్లీ సుల్తానులు భారతదేశానికి ఢిల్లీ నగరాన్ని రాజధానిగా చేసుకుని పరిపాలించారు.

→ గతాన్ని అధ్యయనం చేయడమే చరిత్ర.

→ చారిత్రక ఆధారాలను స్థూలంగా రెండు రతాలుగా వర్గీకరించారు. అవి :

1. పురావస్తు ఆధారాలు,
2. వాజ్మయ (లిఖిత) ఆధారాలు.

→ ప్రాచీన యుగం – క్రీ.శ. 8వ శతాబ్దం వరకు
మధ్య యుగం – క్రీ.శ. 8 నుండి 18 శతాబ్దం వరకు
ఆధునిక యుగం – క్రీ.శ. 18వ శతాబ్దం నుండి ప్రస్తుతం

→ తోమార వంశానికి చెందిన రాజపుత్రులు దిల్లిక లేదా దిల్లికాపుర (ప్రస్తుత ఢిల్లీ) నిర్మించి రాజధానిగా చేసుకుని పరిపాలించారు.

→ క్రీ.శ. 1192వ సంవత్సరంలో మహ్మద్ ఘోరి రెండవ తతాయివ్ యుద్ధంలో పృథ్వీరాజ్ చౌహాన్ ను ఓడించి ఢిల్లీని స్వాధీనం చేసుకున్నాడు.

→ మహ్మద్ ఘోరి హత్యానంతరం అతని ప్రతినిధి అయిన కుతుబుద్దీన్ ఐబక్ మామ్లుక్ లేదా బానిస వంశాన్ని క్రీ. శ. 1206లో ఢిల్లీ పాలకునిగా ఢిల్లీ సుల్తానుల సామ్రాజ్యాన్ని స్థాపించాడు.

→ మొదట లాహోర్ రాజధానిగా ఢిల్లీ సామ్రాజ్యాన్ని ఐబక్ స్థాపించాడు.

→ ఇల్ టుట్ మిష్ కాలంలో రాజధాని ఢిల్లీకి మార్చబడినది.

→ ఇల్ టుట్ మిష్ ఢిల్లీకి తొలి సర్వ స్వతంత్ర పాలకునిగా, ఢిల్లీ సామ్రాజ్యానికి అసలైన స్థాపకునిగా పరిగణింపబడతాడు.

→ ఇల్ టుట్ మిష్ తరువాత ఇతని కుమార్తె రజియా సుల్తానా ఢిల్లీ సింహాసనాన్ని అధిష్టించారు.

→ బానిస వంశ పరిపాలన ‘కైకుబాదు’ కాలంలో ముగిసింది.

→ సుల్తానా రజియా (1236 – 1239) ఢిల్లీని పాలించిన ఏకైక మహిళ.

→ ఖిల్జీ వంశ స్థాపకుడు జలాలుద్దీన్ ఖిల్జీ.

→ అల్లావుద్దీన్ ఖిల్జీ (1296- 1316) గూఢచారి వ్యవస్థను స్థాపించాడు.

→ అల్లావుద్దీన్ ఖిల్జీ దక్షిణ భారతదేశాన్ని జయించడానికి మాలిక్ కాఫర్ ఆధ్వర్యంలో సైన్యాన్ని పంపించాడు.

→ అల్లావుద్దీన్ ఖిల్జీ మార్కెట్ సంస్కరణల్లో భాగంగా వస్తువుల ధరను క్రమబద్ధీకరించాడు.

→ అల్లావుద్దీన్ ఖిల్జీ గుర్రాలు బదిలీ కాకుండా వాటిపై ముద్ర వేసే పద్ధతిని ప్రవేశపెట్టాడు.

→ చంగిజ్ ఖాన్ మంగోలియన్లను ఏకం చేసి 1206వ సంవత్సరంలో మంగోల్ రాజ్యాన్ని స్థాపించాడు.

→ మంగోలులు క్రీ.శ. 1221-1368 వరకు భారతదేశంపై అనేక సార్లు దండయాత్ర చేసారు.

→ ఖిల్జీలలో చివరి పాలకుడైన ‘ఖుస్రూ’ పాలనను అంతం చేసి ఘియాసుద్దీన్ తుగ్లక్, తుగ్లక్ వంశాన్ని స్థాపించాడు.

→ మహ్మద్ బీన్ తుగ్లక్ (1324-1351) రాజధానిని ఢిల్లీ నుండి దేవగిరి (దౌలతాబాద్)కి మార్చాడు. రాగి నాణాలు ముద్రించాడు. వ్యవసాయ సంస్కరణలు చేపట్టాడు.

→ సయ్యద్ వంశ స్థాపకుడు కిజర్ ఖాన్.

→ సయ్యద్ వంశ చివరి పాలకుడు ఆలమ్ షా బహలాల్ చేతిలో ఓడిపోవటంతో లోడి వంశ పాలన సంక్రమించింది. ఢిల్లీ సుల్తానులలో చివరి పాలకుడైన ఇబ్రహీం లోడీని మొఘల్ వంశస్థుడైన బాబర్ ఓడించి, భారతదేశంలో మొఘల్ వంశ స్థాపన చేసాడు.

→ తుగ్లక్ వంశ పాలనా కాలంలో క్రీ. శ. 1398వ సంవత్సరంలో తైమూర్ భారతదేశంపై దండయాత్ర చేసి ఢిల్లీని స్వాధీనపరచుకున్నాడు.

→ ఢిల్లీ సుల్తానుల కాలంలో సుల్తాన్ సర్వాధికారి.

→ ఢిల్లీ సుల్తానుల కాలంలో షరియత్ లేదా ఇస్లామిక్ నిబంధనల ప్రకారం పరిపాలన జరుగుతుంది.

→ రాజ్యాన్ని ఇకాలు, పరగణాలు, షికు మరియు గ్రామాలుగా విభజించారు.

→ గ్రామ పరిపాలనలో కేంద్రం జోక్యం చేసుకోదు.

→ ఇల్ టుట్ మిష్ సైనిక అవసరాల కోసం బానిసలను కొనుగోలు చేసేవాడు. పర్షియాలో ఈ పద్ధతిని ‘బందగాన్’ అని పిలుస్తారు.

→ ఇల్ టుట్ మిష్ కాలంలో చిహల్ గని సర్దారులు కీలక పాత్ర పోషించారు.

→ పరిపాలనలో సహకరించడం కోసం టర్కిష్ ప్రభువులతో కూడిన వ్యవస్థనే తుర్కాన్-ఇ-చిహల్ గని లేదా చాలీసా అనేవారు.

→ ఢిల్లీ సుల్తానులు తమ రాజ్యాన్ని ఇకాలుగా విభజించారు.

→ ఇక్తా సైనికాధికారులను ఇక్తాదార్లు లేదా ముకీలు అంటారు.

→ ఇక్తాదార్ పదవి వారసత్వముగా ఉండేది కాదు, తరచుగా బదిలీలు ఉండేవి.

→ వ్యవసాయము ప్రధాన వృత్తి. 1/3వ వంతు శిస్తు చెల్లించాలి.

→ పత్తి, ముత్యాలు, ధాన్యం, నీలిమందు మొదలైనవి ప్రధాన ఎగుమతులు.

→ టంకా (వెండి), జిటాల్ (రాగి) నాణేలు ప్రామాణిక నాణేలుగా వాడుకలో ఉండేవి.

→ ఢిల్లీ సుల్తానుల కాలంలో అరబిక్ మరియు ఇస్లాం శైలుల మిశ్రమంతో కూడిన వాస్తు నిర్మాణాలు, కళలు అభివృద్ధి చెందాయి.

→ స్వదేశీ నిర్మాణాలలో ట్రూబీట్ పద్ధతి తర్వాత అర్క్యుట్ పద్ధతి ప్రవేశపెట్టబడింది.

→ కుతుబ్ మినార్‌ను కువ్వత్-ఉల్-ఇస్లాం మసీదు ఆవరణలో నిర్మించారు.

→ కుతుబ్ మినారను కుతుబుద్దీన్ ఐబక్, ఇల్ టుట్ మిషన్లు కట్టించి సూఫి సన్యాసి అయిన కుతుబుద్దీన్ భక్తియార్ ఖాకీకి అంకితం ఇచ్చారు.

→ అలైదర్వాజాను అల్లావుద్దీన్ ఖిల్జీ కువ్వత్-ఉల్-ఇస్లామ్ మసీదుకు దక్షిణ ద్వారం వలే నిర్మించాడు.

→ తారిక్-అల్-హింద్ (భారతదేశ చరిత్ర) అనే గ్రంథాన్ని అల్ బెరూని రచించాడు.

→ అమీర్ ఖుస్రూ అనేక ద్విపద పద్యాలు రచించాడు.

→ అమీర్ ఖుస్రూకు భారతదేశపు చిలుక (టుటి-ఐ-హింద్) అనే బిరుదు కలదు.

→ 1398 తైమూరు దండయాత్రలలో దేశ సంపదని తరలించి వేశారు.

→ క్రీ.శ. 1526లో మొఘల్ పాలకుడైన బాబర్ మొదటి పానిపట్టు యుద్ధంలో ఇబ్రహీం లోడీని ఓడించాడు.

→ బానిస వంశం-కుతుబుద్దీన్ ఐబక్ స్థాపకుడు, కాలం : 1206-1290

→ ఖిల్జీ వంశం-జలాలుద్దీన్ ఖిల్జీ స్థాపకుడు, కాలం : 1290-1320

→ తుగ్లక్ వంశం-ఘియాజుద్దీన్ తుగ్లక్ స్థాపకుడు, కాలం : 1321-1414

→ సయ్యద్ వంశం-కిజరిన్ స్థాపకుడు, కాలం : 1414-1451

→ లోడి వంశం-బహలాల్ లోడి స్థాపకుడు, కాలం : 1451-1526

→ చరిత్ర : గతాన్ని అధ్యయనం చేయడమే చరిత్ర.

→ పురావస్తు ఆధారాలు : పురావస్తు సముదాయములైన (నాణాలు, శాసనాలు, స్మారకాలు, కళాఖండములు) ప్రాచీన నాగరికతా అవశేష సంపద.

→ వాజ్మయ ఆధారాలు : లిఖిత ఆధారాలు, సాహిత్య (సారస్వత) ఆధారాలు.

→ ప్రాచీన యుగం : 8వ శతాబ్దం వరకు

→ మధ్య యుగం : 8 నుండి 18వ శతాబ్దం వరకు

→ ఆధునిక యుగం : 18వ శతాబ్దం నుండి ప్రస్తుతం

→ వజీరులు : ఢిల్లీ సుల్తానుల మంత్రులు

→ సంచార జాతులు : ‘ఒక చోట స్థిర నివాసం ఏర్పరుచుకోని జాతులు. నిరంతరం ఒక ప్రాంతం నుండి మరొక ప్రాంతానికి వెళ్ళేటటువంటివారు.

→ సుల్తాన్ : రాజ్యంలో సర్వాధికారి (రాజు).

→ చిహల్గని : పరిపాలనలో సహకరించడం కొరకు టర్కిష్ ప్రభువులతో కూడిన వ్యవస్థ. దీనిని ఇల్ టుట్ మిష్ ప్రారంభించాడు.

→ బందగాన్ : సైనిక అవసరాల కోసం బానిసలను కొనుగోలు చేసే పద్ధతిని పర్షియాలో బందగాన్ అంటారు.

→ ఇక్షాలు : ఢిల్లీ సుల్తానుల కాలం నాటి రాష్ట్రాలు.

→ ఇక్టాదార్ (ముక్తీలు) : ఇకాల యొక్క సైనికాధికారులు.

→ ట్రూబీట్ శైలి : రెండు నిలువు స్తంభాలపై అడ్డంగా ఒక దూలము పెట్టి దానిపై కప్పులు, తలుపులు, కిటికీలు మొదలైనవి తయారుచేయబడేవి.

→ ఆర్క్యుట్ శైలి : తలుపులు, కిటికీలపై ప్రత్యేకంగా ఉండి వాటిపై గల బరువును మోయునట్లుగా ఆర్చి నిర్మాణం ఉంటుంది.

→ రాజవంశం : వారసత్వంగా వచ్చే పాలకుల పరంపర.

→ ప్రకటన : అధికారికంగా వెల్లడి చేసిన సమాచారం.

→ దోహాలు : రెండు పంక్తులలో వ్రాయబడిన పద్యాలు. వీటిలో పాదంలోని పదాలు, లయ దాదాపు సమానంగా ఉంటాయి.

→ కార్యానా : పరిశ్రమలు / కార్యశాలలు

→ షరియత్ : ఇస్లాం న్యాయ సూత్రాలు

1.

2.

3.

4.