Inter 2nd Year

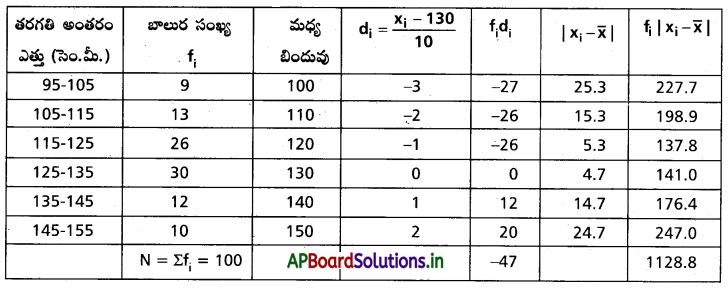
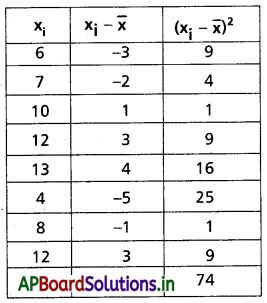
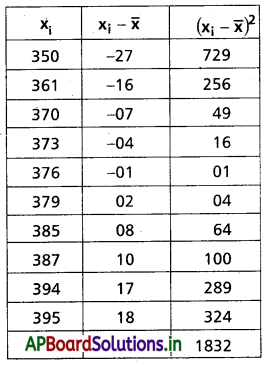
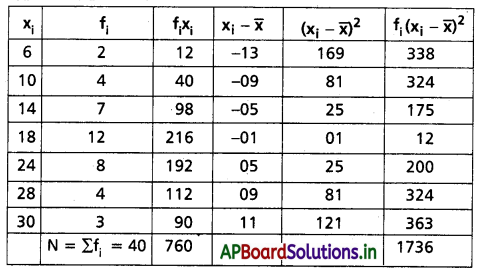
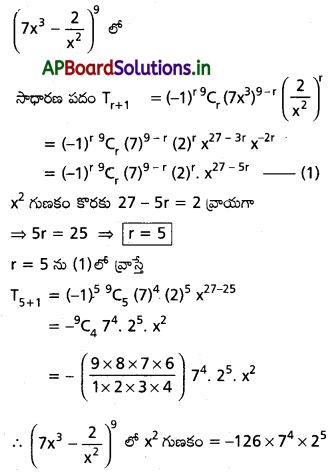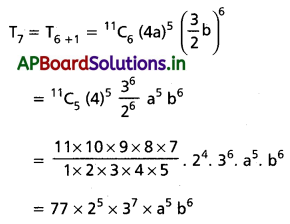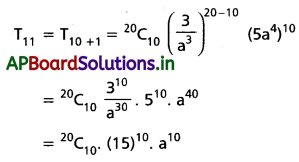Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 9 సంభావ్యత Exercise 9(c) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 9 సంభావ్యత Exercise 9(c)

అభ్యాసం – 9(సి)

I.

ప్రశ్న 1.
ఒక గుట్టలో గల 50 స్కూలలో 5 చెడిపోయినవి. ఈ గుట్టలో నుంచి మూడు స్క్రూలను యాదృచ్ఛికంగా తీశారు. (a) తీసిన స్కూలను తిరిగి భర్తీ చేసే విధంగా (b) తీసిన స్క్రూలను తిరిగి భర్తీ చేయని విధంగా వీటిని ఎంపిక చేశారనుకుంటే, మూడు స్క్రూలు పనిచేసేవి అయ్యే సంభావ్యతను కనుక్కోండి.
సాధన:
మొత్తం స్క్రూల సంఖ్య = 50
అందు చెడిపోయినవి = 5
మంచివి = 45
E అనేది 3 స్క్రూలు చెడిపోయినవి అయ్యే ఘటన.
(a) ఒక స్క్రూను ఎన్నుకొన్న వెంటనే తిరిగి అందులోకే చేర్చడం.
P(E) = \(\frac{{ }^{45} C_1}{{ }^{50} C_1} \times \frac{{ }^{45} C_1}{{ }^{50} C_1} \times \frac{{ }^{45} C_1}{{ }^{50} C_1}\) {తీసిన స్క్రూలను తిరిగి భర్తీ చేయబడినది}
= \(\frac{45}{50} \times \frac{45}{50} \times \frac{45}{50}\)
= \(\frac{9}{10} \times \frac{9}{10} \times \frac{9}{10}\)
= \(\left(\frac{9}{10}\right)^3\)
(b) ఒక స్క్రూను ఎన్నుకొన్న వెంటనే తిరిగి అందులోకి చేర్చకపోవడం
P(E) = \(\frac{{ }^{45} C_1}{{ }^{50} C_1} \times \frac{{ }^{44} C_1}{{ }^{49} C_1} \times \frac{{ }^{43} C_1}{{ }^{48} C_1}\)
= \(\frac{45}{50} \times \frac{44}{49} \times \frac{43}{48}\)
= \(\frac{1419}{1960}\)

ప్రశ్న 2.
ఒక యాదృచ్ఛిక ప్రయోగంలో A, B, C లు మూడు స్వతంత్ర ఘటనలవుతూ P(A ∩ B^C ∩ C) = \(\frac{1}{4}\), P(A^C ∩ B ∩ C^C) = \(\frac{1}{8}\)‚ P(A^C ∩ B^C ∩ C^C) = \(\frac{1}{4}\) అయినప్పుడు P(A), P(B), P(C) లను కనుక్కోండి.
సాధన:
A, B, C లు మూడు స్వతంత్ర ఘటనలు

ప్రశ్న 3.
ఒక సంచిలో 3 నల్లని, 4 తెల్లని బంతులు ఉన్నాయి. రెండో సంచిలో 4 నల్లని, 3 తెల్లని బంతులు ఉన్నాయి. ఒక పాచికను, దొర్లించి దానిపై 1 లేదా 3 పడినప్పుడు మొదటి సంచిని ఎంపిక చేస్తారు. మిగిలిన సందర్భాలలో రెండో సంచిని ఎంపిక చేస్తారు. ఒక సంచిని ఈ విధంగా ఎంపిక చేసినప్పుడు ఒక నల్లని బంతిని తీసే సంభావ్యతను కనుక్కోండి.
సాధన:
పాచికపై 1 లేదా 3 పడినప్పుడు మొదటి సంచిని ఎంపిక చేస్తారు.
∴ మొదటి సంచిని ఎన్నుకొనేందుకు సంభావ్యత = \(\frac{2}{6}=\frac{1}{3}\)
∴ రెండవ సంచిని ఎన్నుకొనేందుకు సంభావ్యత = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
మొదటి సంచిని ఎంపికచేసి అందులో నల్లబంతి తీసేందుకు సంభావ్యత = \(\frac{1}{3} \times \frac{3}{7}=\frac{3}{21}\)
ఇక రెండవ సంచిని ఎంపికచేసి అందులో నల్ల బంతి తీసేందుకు సంభావ్యత = \(\frac{2}{3} \times \frac{4}{7}=\frac{8}{21}\)
∴ ఎన్నుకొన్న సంచి నుంచి నల్లని బంతి వచ్చే సంభావ్యత = \(\frac{3}{21}+\frac{8}{21}=\frac{11}{21}\)

ప్రశ్న 4.
A, B, C లు ఒక బుడగను పేల్చడానికి ప్రయత్నం చేస్తారు. 5 ప్రయత్నాలలో 4 సార్లు A సఫలమవుతాడు. 4 ప్రయత్నాలలో 3 సార్లు B, 3 ప్రయత్నాలలో 2 సార్లు C సఫలం అవుతారు. ముగ్గురు ఏకకాలంలో బుడగను పేల్చడానికి సంసిద్ధం అయితే, కనీసం ఇద్దరు బుడగను పేల్చివేసే సంభావ్యతను కనుక్కోండి.
సాధన:
A అనేవాడు బుడగను పేల్చడానికి సంభావ్యత P(A) = \(\frac{4}{5}\)

వారి ముగ్గురిలో కనీసం ఇరువురు బుడగను పేల్చడానికి సంభావ్యత.
A, B, C లు స్వతంత్ర ఘటనలు

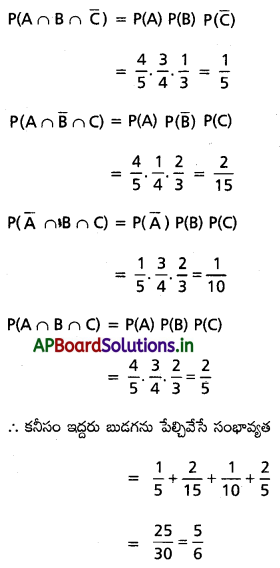
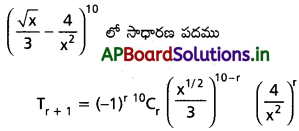
ప్రశ్న 5.
A, B లు రెండు ఘటనలైతే \(P\left(\frac{A}{B}\right) P(B)+P\left(\frac{A}{B^C}\right) P\left(B^C\right)=P(A)\) అని చూపండి.
సాధన:

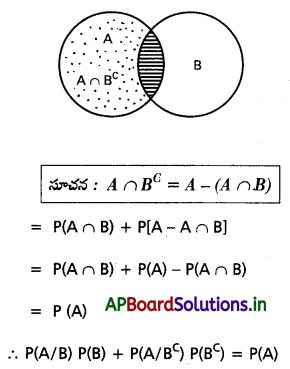
ప్రశ్న 6.
ఒక జత పాచికలను దొర్లించారు. ఏ పాచిక 2ను చూప నట్లయితే, ఆ పాచికలపై మొత్తం 7 రాగల సంభావ్యత ఎంత?
సాధన:
A అనేది రెండు పాచికలపై మొత్తం 7 రాగల ఘటన. అప్పుడు
A = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
B అనేది ఏ పాచిక 2 ను చూపనట్టి ఘటన.
B = {(1,1), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 3), (6, 4), (6, 5), (6, 6)}
n(B) = 25
A ∩ B = ((1, 6), (3, 4), (4, 3), (6, 1)}
n(A ∩ B) = 4
కావలసిన సంభావ్యత
\(P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}=\frac{n(A \cap B)}{n(B)}=\frac{4}{25}\)

ప్రశ్న 7.
ఒక జత పాచికలను దొర్లించారు. ఆ పాచికలపై మొత్తం 7 అయినప్పుడు, ఏ ఒక పాచిక రెండు చూపకపోయే సంభావ్యతను కనుక్కోండి.
సాధన:
పాచికలపై మొత్తం 7 రావటం అనే ఘటన A అనుకుంటే,
A = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
∴ n(A) = 6
ఏ ఒక పాచిక రెండు చూపకపోవటం అనే ఘటన B అనుకుంటే,
B = {(1,1), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 3), (5, 4), (5, 5), (5, 6) (6, 1), (6, 3), (6, 4), (6, 5), (6, 6)}
A ∩ B = {(1, 6), (3, 4), (4, 3), (6, 1)}
n(A ∩ B) = 4
∴ కావలసిన సంభావ్యత
\(P\left(\frac{B}{A}\right)=\frac{P(A \cap B)}{P(A)}=\frac{n(A \cap B)}{n(A)}=\frac{4}{6}=\frac{2}{3}\)

ప్రశ్న 8.
A, B లు ఒక యాదృచ్ఛిక ప్రయోగంలోని ఘటనలు; P(B) ≠ 1, \(P\left(\frac{A}{B^C}\right)=\frac{P(A)-P(A \cap B)}{1-P(B)}\) అని చూపండి.
సాధన:
నియత సంభావ్యతా నిర్వచనం నుండి
\(P\left(\frac{A}{B^C}\right)=\frac{P\left(A \cap B^C\right)}{P\left(B^C\right)}=\frac{P(A)-P(A \cap B)}{1-P(B)}\)
[∵ A ∩ B^C = A – (A ∩ B), P(B^C) = 1 – P(B)]

ప్రశ్న 9.
ఒక పాత్రలో 12 ఎర్రని బంతులు, 12 ఆకుపచ్చని బంతులు ఉన్నాయి. ఒకదాని వెంబడి మరొకటి, భర్తీ చేయని విధంగా రెండు బంతులను తీశారు. మొదట తీసిన బంతి ఎర్రనిది అయినప్పుడు, రెండో బంతి ఆకుపచ్చనిది కాగల సంభావ్యతను కనుక్కోండి.
సాధన:
పాత్రలోని బంతుల సంఖ్య = 12 + 12 = 24
అందులో ఒక బంతిని ఎన్నుకొనే విధానాలు = ²⁴C₁ = 24 = n(S)
E₁ అనేది మొదటిసారి తీసిన బంతి ఎర్రనిది అయ్యే ఘటన
n(E₁) = ¹²C₁ = 12
P(E₁) = \(\frac{n\left(E_1\right)}{n(S)}=\frac{12}{24}=\frac{1}{2}\)
మొదటిసారి తీసిన బంతి సంచిలో చేర్చలేదు కనుక ఇప్పుడు సంచిలోని బంతుల సంఖ్య = 23
రెండవసారి తీసిన బంతి ఆకుపచ్చనిది అయ్యే ఘటన E₂ అనుకుందాం.
\(P\left(\frac{E_2}{E_1}\right)=\frac{12}{23}\)
P(E₁ ∩ E₂) = P(E₁) . P(E₁/E₂)
కావలసిన సంభావ్యత = \(\frac{1}{2} \times \frac{12}{23}=\frac{6}{23}\)

ప్రశ్న 10.
ఒక పాచికను, వరుసగా 2 సార్లు దొర్లించారు. రెండో ప్రయత్నంలో చూపే సంఖ్య, మొదటి ప్రయత్నంలో చూపే సంఖ్య కంటే పెద్దది కాగల సంభావ్యత ఎంత?
సాధన:
ఒక పాచికను వరుసగా రెండుసార్లు దొర్లించారు.
కనుక n(S) = 6 × 6 = 36
E అనేది మొదటి ప్రయత్నంలో దొర్లించినప్పుడు పాచికపై వచ్చే సంఖ్య కంటే రెండో ప్రయత్నంలో దొర్లించినప్పుడు దానిపై వచ్చే సంఖ్య పెద్దది అయ్యే ఘటన
E = {(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6)}
n(E) = 15
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{15}{36}=\frac{5}{12}\)

ప్రశ్న 11.
ఒక చీట్ల పేక కట్ట నుంచి ఒక పేక ముక్కను యాదృచ్ఛికంగా తీశారు. తీసినది ఆసు అయ్యే ఘటన, ఆటీను అయ్యే ఘటన స్వతంత్ర ఘటనలని చూపండి. [May ’13]
సాధన:
ఒక చీట్లపేక కట్టనుంచి ఒక ముక్కను యాదృచ్ఛికంగా తీస్తే ఆసు అయ్యే ఘటన A అని, ఆటీను అయ్యే ఘటన B అని అనుకొనుము.
∴ P(A) = \(\frac{4}{52}=\frac{1}{13}\)
P(B) = \(\frac{13}{52}=\frac{1}{4}\)
A ∩ B అనునది ఆటీను ఆసు అయ్యే ఘటన
P(A ∩ B) = \(\frac{1}{52}=\frac{1}{13} \cdot \frac{1}{4}\) = P(A) . P(B)
∴ A, B లు స్వతంత్ర ఘటనలు.

ప్రశ్న 12.
A అనే బాలుడు స్కాలర్షిప్ పొందే సంభావ్యత 0.9, B అనే మరో బాలుడు స్కాలర్షిప్ పొందే సంభావ్యత 0.8, వీరిలో కనీసం ఒకరు స్కాలర్షిప్ పొందే సంభావ్యత ఎంత?
సాధన:
బాలుడు A స్కాలర్షిప్ పొందడానికి సంభావ్యత P(A) = 0.9
బాలుడు B స్కాలర్షిప్ పొందడానికి సంభావ్యత P(B) = 0.8
A, B లు స్వతంత్ర ఘటనలు
P(A ∪ B) = P(A) + P(B) – P(A) P(B)
= 0.9 + 0.8 – (0.9) (0.8)
= 1.7 – 0.72
= 0.98
n(S) = ⁵²C₁ = 52
n(A) = ⁴C₁ = 4
n(B) = ¹³C₁ = 13
∴ A, B లో కనీసం ఒకరు స్కాలర్షిప్ పొందడానికి సంభావ్యత = P(A ∪ B) = 0.98

ప్రశ్న 13.
P(A ∪ B) = 0.65, P(A ∩ B) = 0.15 అయ్యేటట్లు A, Bలు రెండు ఘటనలు. అప్పుడు P(A^C) + P(B^C) విలువను కనుక్కోండి. [May ’11; Mar. ’05]
సాధన:
A, B లు రెండు ఘటనలు.
P(A ∪ B) = 0.65, P(A ∩ B) = 0.15
∵ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ 0.65 = P(A) + P(B) – 0.15
⇒ P(A) + P(B) = 0.65 + 0.15 = 0.80
ఇప్పుడు P(A^C) + P(B^C) = [1 – P(A)] + [1 – P(B)]
= 2 – (P(A) + P(B))
= 2 – 0.80
= 1.2
∴ P(A^C) + P(B^C) = 1.2

ప్రశ్న 14.
A, B, C స్వతంత్ర ఘటనలు అయితే, A ∪ B మరియు C కూడా స్వతంత్ర ఘటనలని చూపండి.
సాధన:
A, B, C లు స్వతంత్ర ఘటనలు కనుక A, B; B, C; C, Aలు కూడా స్వతంత్ర ఘటనలే.
P(A ∩ B ∩ C) = P(A) P(B) P(C) ……(1)
P(A ∩ C) = P(A) . P(C)
P(B ∩ C) = P(B) . P(C)
P[(A ∪ B) ∩ C] = P[(A ∩ C) ∪ (B ∩ C)]
= P(A ∩ C) + P(B ∩ C) – P[(A ∩ C) ∩ (B ∩ C)]
= P(A) . P(C) + P(B) . P(C) – P(A ∩ B ∩ C)
= P(A) . P(C) + P(B) . P(C) – P(A) . P(B) . P(C)
= P(C) [P(A) + P(B) – P(A) – P(B)]
= P(C) [P(A ∪ B)]
∴ P[(A ∪ B) ∩ C) = P(A ∪ B) . P(C)
కనుక A ∪ B, C లు స్వతంత్ర ఘటనలు.

ప్రశ్న 15.
రెండు ఘటనలు జరిగే సంభావ్యత \(\frac{1}{6}\) అయ్యేటట్లు, రెండూ జరగకపోవడానికి గల సంభావ్యత \(\frac{1}{3}\) అయ్యేటట్లుగా A, B లు రెండు స్వతంత్ర ఘటనలు. P(A) ను కనుక్కోండి.
సాధన:
A, B లు స్వతంత్ర ఘటనలు
P(A ∩ B) = \(\frac{1}{6}\)
⇒ P(A) . P(B) = \(\frac{1}{6}\) …….(1)

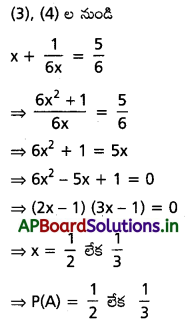
ప్రశ్న 16.
ఒక నిష్పాక్షిక పాచికను దొర్లించారు.
A = {1, 3, 5}, B = {2, 3}, C = {2, 3, 4, 5} ఘటనలను తీసుకోండి.
(i) P(A ∩ B), P(A ∪ B) (ii) \(P\left(\frac{A}{B}\right), P\left(\frac{B}{A}\right)\) (iii) \(P\left(\frac{A}{C}\right), P\left(\frac{C}{A}\right)\) (iv) \(P\left(\frac{B}{C}\right), P\left(\frac{C}{B}\right)\) లను కనుక్కోండి.
సాధన:
ఒక పాచికను దొర్లించారు.
n(S) = 6
∵ A = {1, 3, 5)
⇒ P(A) = \(\frac{3}{6}=\frac{1}{2}\)
B = {2, 3)
⇒ P(B) = \(\frac{2}{6}=\frac{1}{3}\)
C = {2, 3, 4, 5}
⇒ P(C) = \(\frac{4}{6}=\frac{2}{3}\)
(i) A ∩ B = {3}
∴ P(A ∩ B) = \(\frac{1}{6}\)
A ∪ B = {1, 2, 3, 5}
P(A ∪ B) = \(\frac{4}{6}=\frac{2}{3}\)

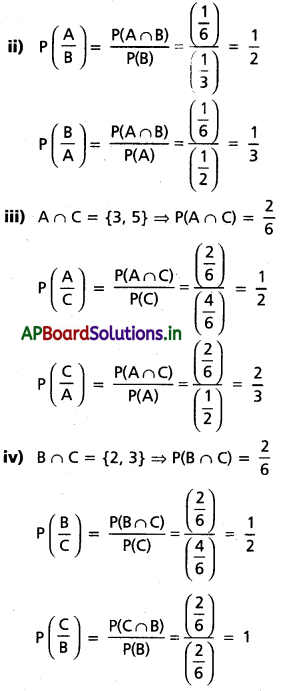
ప్రశ్న 17.
A, B, C ఒక యాదృచ్ఛిక ప్రయోగంలోని మూడు ఘటనలు. క్రింది వాటిని నిరూపించండి.
(i) \(P\left(\frac{A}{A}\right)\) = 1
సాధన:
\(P\left(\frac{A}{A}\right)=\frac{P(A \cap A)}{P(A)}=\frac{P(A)}{P(A)}=1\)

(ii) \(P\left(\frac{\phi}{A}\right)\) = 0
సాధన:
\(P\left(\frac{\phi}{A}\right)=\frac{P(A \cap \phi)}{P(A)}=\frac{P(\phi)}{P(A)}=\frac{0}{P(A)}=0\)

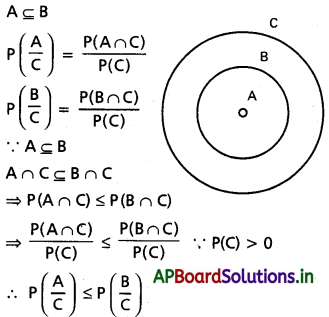
(iii) A ⊆ B ⇒ \(P\left(\frac{A}{C}\right) \leq P\left(\frac{B}{C}\right)\)
సాధన:

(iv) P(A – B) = P(A) – P(A ∩ B)
సాధన:
A – B = {x/x ∈ A ∩ x ∉ B}
∴ A-B = A – (A ∩ B)

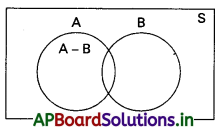
P(A – B) = P[A – (A ∩ B) = P(A) – P(A ∩ B)]

(v) A, B లు పరస్పర వివర్జితాలై, P(B) > 0 అయితే \(P\left(\frac{A}{B}\right)\) = 0.
సాధన:
A, B లు పరస్పర వివర్జితాలు.
∴ A ∩ B = φ
\(P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}=\frac{P(\phi)}{P(B)}=\frac{0}{P(B)}=0\)

(vi) A, B లు పరస్పర వివర్జితాలైతే, \(P\left(\frac{A}{B^C}\right)=\frac{P(A)}{1-P(B)}\); P(B) ≠ 1.
సాధన:
A, B లు పరస్పర వివర్జిత ఘటనలు.
A ∩ B = φ
∴ P(A ∩ B) = 0

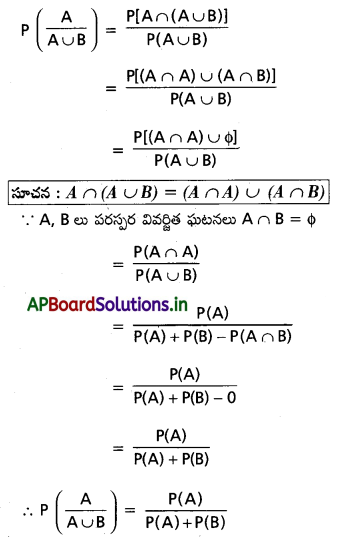
(vii) A, B పరస్పర వివర్జితాలైతే, P(A ∪ B) ≠ 0 అయితే \(\mathbf{P}\left(\frac{\mathbf{A}}{\mathbf{A} \cup \mathbf{B}}\right)=\frac{\mathbf{P}(\mathbf{A})}{\mathbf{P}(\mathbf{A})+\mathbf{P}(\mathbf{B})}\)
సాధన:

ప్రశ్న 18.
ఒక నాణేన్ని మూడుసార్లు ఎగురవేశారనుకోండి. మూడు బొమ్మలు వచ్చే ఘటన A, మొదటిసారి ఎగురవేసినప్పుడు బొమ్మ వచ్చే ఘటన B అనుకోండి. అప్పుడు A, B లు అస్వతంత్ర ఘటలని చూపండి.
సాధన:
నాణేన్ని మూడు సార్లు ఎగురవేశారు కనుక
n(S) = 2³ = 8
A అనేది 3 బొమ్మలు వచ్చే ఘటన
n(A) = ³C₃ = 1
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{1}{8}\)
B అనేది మొదటిసారి ఎగురవేసినపుడు బొమ్మ వచ్చే ఘటన.
B{(HTT), (HHT), (HHH), (HTH)}
P(B) = \(\frac{4}{8}=\frac{1}{2}\)
A ∩ B = {HHH}
n(A ∩ B) = 1
P(A ∩ B) = \(\frac{1}{8}\)
P(A) . P(B) = \(\frac{1}{8} \times \frac{1}{2}=\frac{1}{16}\)
∴ P(A ∩ B) ≠ P(A) . P(B)
∴ A, B లు అస్వతంత్ర ఘటనలు.

ప్రశ్న 19.
ఒక నిష్పాక్షిక పాచికల యుగ్మాన్ని దొర్లించారు. రెండింటి పై ముఖాలపై ఒకే సంఖ్య వచ్చే ఘటన A అనుకోండి. రెండింటి ముఖాల పైన వచ్చే సంఖ్యల మొత్తం 7 కంటే ఎక్కువ అయ్యే ఘటన B అనుకోండి. అప్పుడు (i) \(P\left(\frac{A}{B}\right)\) (ii) \(P\left(\frac{B}{A}\right)\) లను కనుక్కోండి.
సాధన:
రెండు నిష్పాక్షిక పాచికలను దొర్లించారు. కనుక
n(S) = 36
A అనేది రెండు పాచికలపై ఒకే సంఖ్య వచ్చే ఘటన
A = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6,6)}
n(A) = 6
B అనేది రెండింటి పైన వచ్చే సంఖ్యల మొత్తం 7 కంటే ఎక్కువ అయ్యే ఘటన.
B = {(2, 6), (3, 5), (3, 6), (4, 4), (4, 5) (4, 6), (5, 3), (5, 4), (5, 5), (5, 6) (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(B) = 15
A ∩ B = {(4, 4), (5, 5), (6, 6)}
n(A ∩ B) = 3

ప్రశ్న 20.
A, B లు స్వతంత్ర ఘటనలనడానికి ఆవశ్యక పర్యాప్త నియమం \(P\left(\frac{A}{B}\right)=P\left(\frac{A}{B^C}\right)\) అని చూపండి.
సాధన:
A, B లు స్వతంత్ర ఘటనలు అని నిరూపించటానికి P(A ∩ B) = P(A) . P(B) అని చూపాలి.

II.

ప్రశ్న 1.
P(A) = 0.6, P(B) = 0.75 తో A, B స్వతంత్ర ఘటనలనుకోండి. అప్పుడు (i) P(A ∩ B) (ii) P(A ∪ B) (iii) \(P\left(\frac{B}{A}\right)\) (iv) P(A^C ∩ B^C) లను కనుక్కోండి. [Mar. ’14]
సాధన:
A, B లు స్వతంత్ర ఘటనలు.
P(A) = 0.6, P(B) = 0.7
(i) P(A ∩ B) = P(A) . P(B)
= 0.6 × 0.7
= 0.42
(ii) P(A ∪ B) = P(A) + P(B) – P(A) . P(B)
= 0.6 + 0.7 – 0.42
= 1.3 – 0.42
= 0.88
(iii) \(P\left(\frac{B}{A}\right)\) = P(B) = 0.7
∵ A, B లు స్వతంత్ర ఘటనలు
(iv) P(A^C ∩ B^C) = P(A^C) . P(B^C)
(∵ A, B లు స్వతంత్ర ఘటనలైన A^C, B^C లు కూడా స్వతంత్ర ఘటనలు)
= [1 – P(A)] [1 – P(B)]
= (1 – 0.6) (1 – 0.7)
= (0.4) (0.3)
= 0.12

ప్రశ్న 2.
ఒక క్రికెట్ ఆటలో ఇండియాపై ఆస్ట్రేలియా గెలిచే సంభావ్యత \(\frac{1}{3}\). ఇండియా, ఆస్ట్రేలియా 3 ఆటలలో ఆడితే,
(i) ఆస్ట్రేలియా మూడు ఆటలు ఓడిపోయే సంభావ్యతను,
(ii) ఆస్ట్రేలియా కనీసం ఒక ఆట గెలిచే సంభావ్యతను కనుక్కోండి.
సాధన:
E అనేది ఇండియాపై ఆస్ట్రేలియా గెలిచే ఘటన అనుకుందాం.
P(E) = \(\frac{1}{3}\)
P(\(\bar{E}\)) = 1 – P(E)
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
(i) ఆస్ట్రేలియా మూడు ఆటలు ఓడిపోవడానికి సంభావ్యత = (P(\(\bar{E}\)))3
= \(\left(\frac{2}{3}\right)^3\)
= \(\frac{8}{27}\)
(ii) ఆస్ట్రేలియా కనీసం ఒక ఆట గెలిచే సంభావ్యత = 1 – (P(\(\bar{E}\)))3
= 1 – \(\frac{8}{27}\)
= \(\frac{19}{27}\)

ప్రశ్న 3.
I, II, III అంకెలను కలిగిన మూడు పెట్టెలలో క్రింది విధంగా బంతులు ఉన్నాయి. [A.P. Mar. ’16]

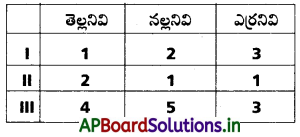
ఒక పెట్టెను ఎంచుకొని అందులోనుంచి ఒక బంతిని యాదృచ్ఛికంగా తీశారు. బంతి ఎర్రనిదైతే అది పెట్టె II నుంచి తీయగల సంభావ్యతను కనుక్కోండి.
సాధన:
E₁, E₂, E₃ లు వరుసగా I, II, III పెట్టెలను ఎన్నుకునే ఘటనలు అనుకుందాం.
P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\)
పెట్టె I నుండి ఎర్ర బంతిని ఎన్నుకోవటానికి సంభావ్యత
P(R/E₁) = \(\frac{3}{6}=\frac{1}{2}\)
ఇట్లే P(R/E₂) = \(\frac{1}{4}\), P(R/E₃) = \(\frac{3}{12}=\frac{1}{4}\)
తీసిన బంతి ఎర్రనిది అయితే అది పెట్టె II నుంచి తీయగల సంభావ్యత (బేయీ సిద్ధాంతం నుంచి)

ప్రశ్న 4.
ఒకనికి నిర్మాణపు కంపెనీలో ఉద్యోగం లభించింది. ఆ కంపెనీలోని పనివారు సమ్మెకు దిగే సంభావ్యత 0.65 సమ్మె లేనప్పుడు నిర్మాణం పని సరైన సమయంలో పూర్తయ్యే సంభావ్యత 0.80. సమ్మె ఉన్నప్పటికీ, నిర్మాణం పని పూర్తయ్యే సంభావ్యత 0.32, అయితే నిర్మాణం పని సరైన సమయంలో పూర్తయ్యే సంభావ్యతను నిర్ధారించండి.
సాధన:
P(S) = కంపెనీలోని పనివారు సమ్మెకు దిగే సంభావ్యత = 0.65
P(\(\bar{S}\)) = కంపెనీలోని పనివారు సమ్మెకు దిగకుండా ఉండుటకు సంభావ్యత
= 1 – P(S)
= 1 – 0.65
= 0.35
\(P\left(\frac{E}{S}\right)\) = సమ్మె ఉన్నప్పటికీ, నిర్మాణం పని పూర్తయ్యే సంభావ్యత = 0.32
\(P\left(\frac{E}{\bar{S}}\right)\) = సమ్మె లేకుండా నిర్మాణ పని సరైన సమయంలో పూర్తయ్యే సంభావ్యత = 0.80
P(E) = నిర్మాణపని సరైన సమయంలో పూర్తి కావడానికి సంభావ్యత
= \(P(S) P\left(\frac{E}{S}\right)+P(\bar{S}) P\left(\frac{E}{\bar{S}}\right)\)
= (0.65) (0.32) + (0.35) (0.08)
= 0.2080 + 0.2800
= 0.4880

ప్రశ్న 5.
ఏవైనా రెండు ఘటనలు A, B లకు P(A ∩ B) – P(A) . P(B) = P(A^C) P(B) – P(A^C ∩ B) = P(A) P(B^C) – P(A ∩ B^C) అని చూపండి.
సాధన:
P(A^C) P(B) – P(A^C ∩ B)
= [1 – P(A)] P(B) – P[B – (A ∩ B)]
= P(B) – P(A) P(B) – P(B) + P(A ∩ B)
= P(A ∩ B) – P(A) P(B)
∴ P(A^C) P(B) – P(A^C ∩ B) = P(A ∩ B) – P(A) P(B) …….(1)
P(A) P(B^C) – P(A ∩ B^C) = P(A) [1 – P(B)] – P[A – (A ∩ B)]
= P(A) – P(A) P(B) – P(A) + P(A ∩ B)
= P(A ∩ B) – P(A) P(B)
∴ P(A) P(B^C) – P(A ∩ B^C) = P(A ∩ B) – P(A) P(B) ……..(2)
∴ (1), (2) ల నుండి,
P(A ∩ B) – P(A) P(B) = P(A^C) P(B) – P(A^C ∩ B) = P(A) P(B^C) – P(A ∩ B^C)

III.

ప్రశ్న 1.
మూడు పాత్రలు క్రింది విధంగా బంతులను కలిగి ఉన్నాయి.
పాత్ర I: 1 తెల్లనిది, 2 నల్లనివి
పాత్ర II: 2 తెల్లనివి, 1 నల్లనివి
పాత్ర III: 2 తెల్లనివి, 2 నల్లనివి
ఒక పాత్రను యాదృచ్ఛికంగా ఎంపికచేసి, దాని నుంచి ఒక బంతిని తీశారు. అది తెల్లనిదిగా గుర్తించారు. ఆ బంతి పాత్ర III నుంచి తీయగల సంభావ్యతను కనుక్కోండి.
సాధన:
i పాత్రను ఎన్నుకొనే ఘటనను E_i (i = 1, 2, 3) తో సూచిస్తే, i అనే పాత్రను ఎన్నుకోవటానికి సంభావ్యత P(E_i)
ఇచ్చట P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\)
i పాత్ర నుండి తెల్లబంతి రావటం అనే ఘటనను (W/E_i) తో సూచిస్తే, దాని సంభావ్యత P(W/E_i) అవుతుంది.
ఇప్పుడు P(W/E₁) = \(\frac{1}{3}\)
P(W/E₂) = \(\frac{2}{3}\)
P(W/E₃) = \(\frac{2}{4}\)
తీసిన బంతి తెల్లనిది అయితే అది పాత్ర III నుంచి రావటానికి సంభావ్యత (బేయీ సిద్ధాంతం నుంచి)

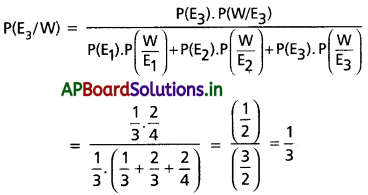
ప్రశ్న 2.
ఒక కాల్పుల పోటీలో A, B, C లక్ష్యాన్ని ఛేదించే సంభావ్యతలు వరుసగా \(\frac{1}{2}, \frac{2}{3}, \frac{3}{4}\). వీరందరూ ఒకే లక్ష్యాన్ని కాల్పులు జరిపినప్పుడు
(i) ఒకే ఒకరు లక్ష్యాన్ని ఛేదించే
(ii) కనీసం ఒకరు లక్ష్యాన్ని ఛేదించే సంభావ్యతలను కనుక్కోండి.
సాధన:
కాల్పుల పోటీలో A, B, C లక్ష్యాన్ని ఛేదించే సంభావ్యతలు వరుసగా

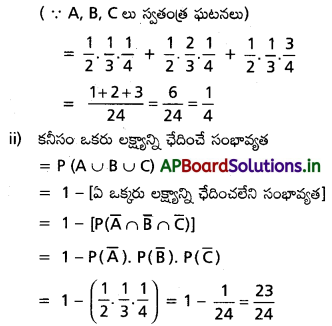
ప్రశ్న 3.
ఒక కళాశాలలో 25% బాలురు, 10% బాలికలు గణితాన్ని అభ్యసిస్తున్నారు. విద్యార్థుల సంఖ్యలో బాలికలు 60% యాదృచ్ఛికంగా ఎంపిక చేసిన ఒక విద్యార్థి గణితం చదువుతున్నట్లయితే, ఆ విద్యార్థి బాలిక కాగల సంభావ్యతను కనుక్కోండి.
సాధన:
ఎన్నుకోబడిన విద్యార్థి బాలిక కాగల సంభావ్యత
P(G) = \(\frac{60}{100}=\frac{6}{10}\)
ఎన్నుకోబడిన విద్యార్థి బాలుడు కాగల సంభావ్యత
P(B) = 1 – P(G)
= 1 – \(\frac{6}{10}\)
= \(\frac{4}{10}\)
బాలుడు గణితం అభ్యసించడానికి సంభావ్యత
P(M/B) = \(\frac{25}{100}=\frac{1}{4}\)
ఇట్లే P(M/G) = \(\frac{10}{100}=\frac{1}{10}\)
ఎంపిక చేసిన విద్యార్థి గణితం చదువుతున్నట్లయితే, ఆ విద్యార్థి బాలిక కాగల సంభావ్యత (బేయీ సిద్ధాంతం ప్రకారం)

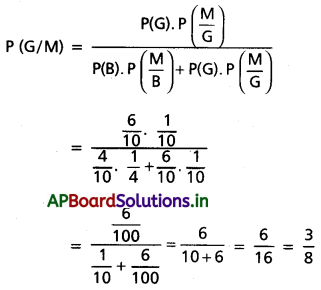
ప్రశ్న 4.
ఒకనికి ‘3’ సార్లలో ‘2’ సార్లు నిజం చెప్పే అలవాటు ఉంది. అతడు ఒక పాచికను దొర్లించి అది ‘1’ అని నివేదిస్తాడు. అది నిజంగా ‘1’ అయ్యే సంభావ్యతను కనుక్కోండి.
సాధన:
P(T) = ప్రతి 3 సార్లలో 2 సార్లు నిజం చెప్తే అంతని సంభావ్యత = \(\frac{2}{3}\)
P(F) = 1 – P(T)
= 1 – \(\frac{2}{3}\)
= \(\frac{1}{3}\)
అతడు 1 అని నివేదించిన తరువాత పాచిక 1 చూపితే నిజం చెప్పినట్లు మరియు 1 చూపకపోతే అబద్ధం చెప్పినట్లు.
P(1) = \(\frac{1}{6}\) మరియు P(T) = \(\frac{5}{6}\)
P(T/1) = P(1 పడితే నిజం చెప్పినట్లు) = \(\frac{2}{3}\)
P(F/T) = P(అబద్ధం చెప్పినట్లు నిజం కాకపోతే) = \(\frac{1}{3}\)
బేయీ సిద్ధాంతం నుంచి

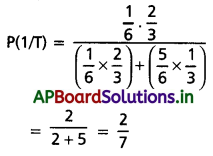
∴ అది నిజంగా 1 అయ్యే సంభావ్యత = \(\frac{2}{7}\)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 9 సంభావ్యత Exercise 9(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 9 సంభావ్యత Exercise 9(b)

అభ్యాసం – 9(బి)

I.

ప్రశ్న 1.
నాలుగు నిష్పాక్షిక నాణేలను ఒకేసారి ఎగురవేసినప్పుడు 2 బొమ్మలు, 2 బొరుసులు పడే సంభావ్యతను కనుక్కోండి. [Mar. ’02]
సాధన:
4 నాణేలను ఒకేసారి ఎగురవేశారు.
∴ n(S) = 2⁴ = 16
E అనేది రెండు బొమ్మలు, రెండు బొరుసులు రావటం అనే ఘటన
n(E) = ⁴C₂
= \(\frac{4 \times 3}{1 \times 2}\)
= 6
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{6}{16}=\frac{3}{8}\)

ప్రశ్న 2.
లీపు సంవత్సరం కాని సందర్భంలో (i) 53 ఆదివారాలు (ii) 52 ఆదివారాలు మాత్రమే వచ్చే సంభావ్యతను కనుక్కోండి. [Mar. ’07, May ’06]
సాధన:
లీపు సంవత్సరం కాని సాధారణ సంవత్సరంలో 365 రోజులుంటాయి. అంటే 52 వారాలు పోగా, ఒకరోజు మిగులుతుంది.
ఆ ఒక్కరోజు ఆది (లేక) సోమ (లేక) మంగళ (లేక) బుధ (లేక) గురు (లేక) శుక్ర (లేక) శనివారం కావచ్చు.
∴ శాంపిల్ ఆవరణ S = {ఆది, సోమ, మంగళ, బుధ, గురు, శుక్ర, శని}
n(S) = 7
(i) E అనేది సాధారణ సంవత్సరంలో 53 ఆదివారాలు ఉండే ఘటన
n(E) = 1
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{1}{7}\)
(ii) ఇక 52 ఆదివారాలు మాత్రమే ఉండే ఘటన సంభావ్యత
P(E^C) = 1 – P(E)
= 1 – \(\frac{1}{7}\)
= \(\frac{6}{7}\)

ప్రశ్న 3.
రెండు పాచికలను దొర్లించారు. ఏ పాచిక 2 ను చూపని సందర్భానికి సంభావ్యత ఎంత?
సాధన:
రెండు పాచికలను దొర్లించారు.
కనుక n(S) = 6² = 36
E అనేది ఏ పాచిక 2 చూపని ఘటన
n(E) = 5 × 5 = 25
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{25}{36}\)

ప్రశ్న 4.
ఒక చీట్లపేక కట్ట నుంచి యాదృచ్ఛికంగా ఒక పేక ముక్కను తీసే ప్రయోగంలో ఇస్ఫేటు ముక్కను తీసే ఘటనను తోను, బొమ్మను కలిగిన కార్డును (రాజు, రాణి లేదా జాకీ) తీసే ఘటనను B తోనూ సూచిద్దాం. అప్పుడు A, B, (A ∩ B), (A ∪ B) ల సంభావ్యతను కనుక్కోండి.
సాధన:
చీట్ల పేక కట్ట నుంచి ఒక పేకను తీసితిరి.
∴ n(S) = ⁵²C₁ = 52
(i) A అనేది తీసిన పేక ముక్క ఇస్ఫేటు కావటం అనే ఘటన
∴ n(A) = ¹³C₁ = 13
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{13}{52}=\frac{1}{4}\)
(ii) B అనేది బొమ్మను కలిగిన కార్డును తీసే ఘటన
∴ n(B) = ¹²C₁ = 12
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{12}{52}=\frac{3}{13}\)
(iii) ఘటన A ∩ B అనేది తీసిన కార్డు బొమ్మను కలిగిన ఇస్ఫేటు కార్డు కావటం అనే ఘటన
∴ n(A ∩ B) = 3
∴ P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{3}{52}\)
(iv) ఘటన A ∪ B అనేది తీసిన పేక ముక్క ఇస్ఫేటు లేదా బొమ్మను కలిగిన కార్డు కావడం అనే ఘటన
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{1}{4}+\frac{3}{13}-\frac{3}{52}\)
= \(\frac{13+12-3}{52}\)
= \(\frac{22}{52}\) లేదా \(\frac{11}{26}\)

ప్రశ్న 5.
60 బాలురు, 20 బాలికలు గల తరగతిలో సగం మంది బాలురు, సగం మంది బాలికలు క్రికెట్పై అవగాహన కలిగినవారు. ఈ తరగతి నుంచి ఒక విద్యార్థిని ఎంపిక చేసినప్పుడు, బాలుడు లేదా క్రికెట్ తెలిసిన వ్యక్తి అయ్యే ఘటనకు సంభావ్యతను కనుక్కోండి.
సాధన:
ఎంపిక చేసినవాడు బాలుడు అయ్యే ఘటన A, ఎంపిక చేసినవారు క్రికెట్ తెలిసిన వ్యక్తి అయ్యే ఘటన B అనుకుందాం.
n(S) = ^{(60 + 20)}C₁ = 80
n(A) = 60, n(B) = (30 + 10) = 40
(∵ సగం మంది బాలురు, సగం మంది బాలికలకు క్రికెట్పై అవగాహన ఉంది.)
A ∩ B అనేది క్రికెట్ తెలిసిన బాలుడు కావటం అనే ఘటన అవుతుంది.
∴ n(A ∩ B) = 30 (సగం మంది బాలురకు క్రికెట్పై అవగాహన ఉంది).
∴ P(A) = \(\frac{60}{80}\), P(B) = \(\frac{40}{80}\), P(A ∩ B) = \(\frac{30}{80}\)
∴ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{60}{80}+\frac{40}{80}-\frac{30}{80}\)
= \(\frac{70}{80}\)
= \(\frac{7}{8}\)

ప్రశ్న 6.
రెండు ఘటనలు A, B లకు P(A^C ∩ B^C) = 1 + P(A ∩ B) – P(A) – P(B) అని చూపండి.
సాధన:
A^C ∩ B^C = (A ∪ B)^C కనుక
P(A^C ∩ B^C) = P[(A ∪ B)^C]
= 1 – P(A ∪ B)
= 1 – [P(A) + P(B) – P(A ∩ B)]
= 1 + P(A ∩ B) – P(A) – P(B)
∴ P(A^C ∩ B^C) = 1 + P(A ∩ B) – P(A) – P(B)

ప్రశ్న 7.
‘ముందుగా 3ను దొర్లించిన వాళ్ళు ఆట గెలిచినట్లు’ అనే షరతుపై A, B అనే ఇద్దరు వ్యక్తులు పాచిక దొర్లించారు. ఆటను ముందుగా A మొదలు పెడితే, A, B లు వరుసగా ఆట గెలిచే సంభావ్యతను కనుక్కోండి.
సాధన:
పాచికను దొర్లించినపుడు ‘3’ చుక్కలున్న ముఖం తిరగబడుటకు సంభావ్యత p = \(\frac{1}{6}\)
∴ సఫల సంభావ్యత p = \(\frac{1}{6}\)
విఫల సంభావ్యత q = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
A గెలిచే ఘటన జరగాలంటే
1. మొదటి యత్నంలోనే A గెలవాలి (ఈ ఘటన సంభావ్యత p) లేదా
2. మొదటి రెండు యత్నాలలో A, B లు ఓడిపోయి, తరువాత యత్నంలో A గెలవాలి.
ఈ ఘటన సంభావ్యత = q . q . p = q²p లేదా
3. మొదటి నాలుగు యత్నాలలో A, B లు ఓడిపోయి ఆ తరువాత యత్నంలో A గెలవాలి.
ఈ ఘటన సంభావ్యత = q . q . q . q . p = q⁴ . p ……
ఈ విధంగా A పాచికపై ‘3’ చుక్కలు వచ్చేవరకు ఆట కొనసాగుతుంది.
పై ఘటనలన్నీ పరస్పర వివర్జితాలు.
∴ సంకలన సిద్ధాంతం నుంచి A గెలుపు సంభావ్యత
P(A) = p + q²p + q⁴P + …..
= p[1 + q² + q⁴ + …..]

∴ B గెలుపు సంభావ్యత = 1 – P(A) = 1 – \(\frac{6}{11}\) = \(\frac{5}{11}\)

ప్రశ్న 8.
A, B, C లు ఒక పట్టణం నుంచి వెలువడే వార్తాపత్రికలు. ఆ పట్టణ జనాభాలో 20% Aని, 16% Bని, 14% C ని, 8% A, B రెండింటిని, 5% A, C రెండింటిని, 4% B, C రెండింటిని, 2% మూడింటినీ చదువుతారు. కనీసం ఒక వార్తాపత్రికను చదివే జనాభా శాతాన్ని కనుక్కోండి.
సాధన:
P(A) = \(\frac{20}{100}\) = 0.2
P(B) = \(\frac{20}{100}\) = 0.16
P(C) = \(\frac{14}{100}\) = 0.14
P(A ∩ B) = \(\frac{8}{100}\) = 0.08
P(B ∩ C) = \(\frac{4}{100}\) = 0.04
P(C ∩ A) = \(\frac{5}{100}\) = 0.05
P(A ∩ B ∩ C) = \(\frac{2}{100}\) = 0.02
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
= 0.2 + 0.16 + 0.14 – 0.08 – 0.04 – 0.05 + 0.02
= 0.52 – 0.17
= 0.35
= \(\frac{35}{100}\)
∴ జనాభాలో కనీసం ఒక పత్రికైనా చదివేవారు = 35%

ప్రశ్న 9.
1 నుంచి 30 వరకు సంఖ్యలను వేసిన 30 టిక్కెట్ల నుంచి యాదృచ్ఛికంగా ఒక టిక్కెట్ను ఎంపికచేస్తే, ఆ టిక్కెట్పై గల సంఖ్య (i) 5 లేదా 7 గుణిజం (ii) 3 లేదా 5 గుణిజం కాగల సంభావ్యతను కనుక్కోండి. [Mar. ’08]
సాధన:
1 నుండి 30 వరకు అంకెలున్న 30 టిక్కెట్ల నుండి యాదృచ్ఛికంగా ఒక టిక్కెట్ ఎన్నుకునే విధాల సంఖ్య
n(S) = ³⁰C₁ = 30
(i) E₁ అనేది ఆ అంకె 5 యొక్క గుణిజం కావటం అనే ఘటన
E₁ = {5, 10, 15, 20, 25, 30}
n(E₁) = 6
P(E₁) = \(\frac{\mathrm{n}\left(E_1\right)}{\mathrm{n}(S)}=\frac{6}{30}=\frac{1}{5}\)
E₂ అనేది ఆ అంకె 7 యొక్క గుణిజం కావటం అనే ఘటన
E₂ = {7, 14, 21, 28}
n(E₂) = 4
P(E₂) = \(\frac{n\left(E_2\right)}{n(S)}=\frac{4}{30}\)
∵ E₁ ∩ E₂ = φ
P(E₁ ∪ E₂) = P(E₁) + P(E₂)
= \(\frac{6}{30}+\frac{4}{30}\)
= \(\frac{10}{30}\)
= \(\frac{1}{3}\)
(ii) E₁ అనేది అంకె 3 యొక్క గుణిజం కావటం అనే ఘటన
E₁ = (3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
n(E₁) = 10
P(E₁) = \(\frac{n\left(E_1\right)}{n(S)}=\frac{10}{30}\)
E₂ అనేది అంకె 5 యొక్క గుణిజం కావటం అనే ఘటన
E₂ = {5, 10, 15, 20, 25, 30)
n(E₂) = 6
P(E₂) = \(\frac{n\left(E_2\right)}{n(S)}=\frac{6}{30}\)
E₁ ∩ E₂ = {15, 30}
P(E₁ ∩ E₂) = \(\frac{2}{30}\)
P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
= \(\frac{10}{30}+\frac{6}{30}-\frac{2}{30}\)
= \(\frac{14}{30}\)
= \(\frac{7}{15}\)

ప్రశ్న 10.
20 వరస సహజ సంఖ్యల నుంచి రెండు సంఖ్యలను యాదృచ్ఛికంగా ఎంపిక చేస్తే, ఆ రెండు సంఖ్యల మొత్తం (i) ఒక సరిసంఖ్య కావడానికి (ii) ఒక బేసి సంఖ్య కావడానికి సంభావ్యతను కనుక్కోండి.
సాధన:
20 వరస సహజ సంఖ్యల నుంచి 2 సంఖ్యలను ఎంపిక చేసే విధానాలు
n(S) = ²⁰C₂
= \(\frac{20 \times 19}{1 \times 2}\)
= 190
వీటిలో 10 బేసిసంఖ్యలు, 10 సరిసంఖ్యలు
(i) E అనేది ఎంపిక చేసిన రెండు సంఖ్యల మొత్తం సరి సంఖ్య కావాలి అనే ఘటన.
రెండు బేసి సంఖ్యల మొత్తం సరి సంఖ్య అవుతుంది లేదా రెండు సరి సంఖ్యల మొత్తం సరి సంఖ్య అవుతుంది.
∴ n(E) = ¹⁰C₂ + ¹⁰C₂
= \(\frac{2(10)(9)}{1 \times 2}\)
= 90
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{90}{190}=\frac{9}{19}\)
(ii) ఎంపిక చేసిన రెండు సంఖ్యల మొత్తం బేసిసంఖ్య కావడానికి సంభావ్యత
P(E^C) = 1 – P(E)
= 1 – \(\frac{9}{19}\)
= \(\frac{10}{19}\)

ప్రశ్న 11.
ఒక నాణేన్ని 3 సార్లు ఎగరవేయడం, వచ్చిన ఫలితాన్ని రాయడం ఒక క్రీడ. అన్ని ఎగరవేతలలోనూ, ఒకే ఫలితం వస్తే ఒక బాలుడు గెలిచినట్లు, అట్లా కాకపోతే ఓడినట్లు భావిస్తారు. ఆ బాలుడు క్రీడలో ఓడిపోయే సంభావ్యతను కనుక్కోండి.
సాధన:
ఒక నాణేన్ని 3 సార్లు ఎగరవేస్తే n(S) = 2³ = 8
అన్ని ఎగరవేతలలోనూ, ఒకే ఫలితం వస్తే, అంటే అన్ని బొమ్మలు లేదా అన్ని అచ్చులు వస్తే బాలుడు గెలిచినట్లుగా భావిస్తారు.
కనుక బాలుడు గెలిచే ఘటన E అయితే
P(E) = \(\frac{2}{8}=\frac{1}{4}\)
∵ E = {HHH, TTT}
∴ ఆ బాలుడు క్రీడలో ఓడిపోయే సంభావ్యత
P(E^C) = 1 – P(E)
= 1 – \(\frac{1}{4}\)
= \(\frac{3}{4}\)

ప్రశ్న 12.
E₁ ∩ E₂ = φ తో E₁, E₂, రెండు ఘటనలు. అప్పుడు \(P\left(E_1^c \cap E_2^c\right)=P\left(E_1^c\right)-P\left(E_2\right)\) అని చూపండి.
సాధన:
E₁ ∩ E₂ = φ
⇒ E₁, E₂ లు పరస్పర వివర్జిత ఘటనలు కనుక
E₁ ∩ E₂ = φ
ఇప్పుడు \(P\left(E_1^c \cap E_2^c\right)\) = P[(E₁ ∪ E₂)^C]
= 1 – P(E₁ ∪ E₂)
= 1 – [P(E₁) + P(E₁)] (∴ E₁, E₂ పరస్పర వివర్జిత ఘటనలు)
= 1 – P(E₁) – P(E₂)
= [1 – P(E₁)] – P(E₂)
= \(P\left(E_1^c\right)\) – P(E₂)

II.

ప్రశ్న 1.
ఒక జత పాచికలను 24 సార్లు దొర్లించారు. ఈ 24 పర్యాయాలలో ఎప్పుడూ ఒక జత 6ను దొర్లించని వ్యక్తి గెలిచినట్లుగా భావిస్తారు. ఆ వ్యక్తి గెలిచే సంభావ్యత ఎంత?
సాధన:
పాచికను 2 సార్లు దొర్లిస్తే పూర్ణ లఘు ఘటనల సంఖ్య = 6 × 6 = 36
రెండు పాచికలను 24 సార్లు దొర్లించారు కనుక n(S) = (36)²⁴
E అనేది దొర్లించిన 24 సార్లలో ఏ ఒక్కసారీ రెండింటిపై 6 రాకపోవటం అనే ఘటన
n(E) = 35 × 35 × ……. × 35 (24 సార్లు) = (35)²⁴
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{(35)^{24}}{(36)^{24}}=\left(\frac{35}{36}\right)^{24}\)

ప్రశ్న 2.
P ఒక సంభావ్యతా ప్రమేయం అయితే, ఏదైనా రెండు ఘటనలు A, B లకు P(A ∩ B) ≤ P(A) ≤ P(A ∪ B) ≤ P(A) + P(B) అని చూపండి.
సాధన:

ఏవేని రెండు సమితులు A, B లకు
A ∩ B ⊆ A ⊆ A ∪ B
P(A ∩ B) ≤ P(A) ≤ P(A ∪ B) ……(1)
సంభావ్యతల సంకలన సిద్ధాంతం నుండి
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
∴ 0 ≤ P(A ∩ B) ≤ 1
⇒ P(A ∪ B) ≤ P(A) + P(B) ……(2)
∴ (1), (2) ల నుండి
P(A ∩ B) ≤ P(A) ≤ P(A ∪ B) ≤ P(A) + P(B)

ప్రశ్న 3.
ఒక పెట్టెలోని 15 బల్బులలో 5 పనిచేయనివి. పెట్టెలో నుంచి యాదృచ్ఛికంగా 5 బల్బులను తీసినప్పుడు, క్రింది ఘటనల సంభావ్యతను కనుక్కోండి.
(i) వాటిలో ఏదీ లోపం లేనిది కావటం అనేది
(ii) వాటిలో ఏదో ఒకటి పని చేయనిది
(iii) వాటిలో కనీసం ఒకటి పనిచేయనిది.
సాధన:
పెట్టెలో ఉన్న 15 బల్బులలో 5 పనిచేయనివి కలిగి ఉన్నవి. మిగిలిన 10 మంచివి.
పెట్టె నుండి యాదృచ్ఛికంగా 5 బల్బులను ఎన్నుకునే విధాలు n(S) = ¹⁵C₅
(i) E₁ అనేది 5 బల్బులు ఏదీ లోపం లేనిది అనే ఘటన అంటే అన్నీ మంచివి కావటం అనే ఘటన
n(E₁) = ¹⁰C₅

ప్రశ్న 4.
A, B లు IIT లో ప్రవేశం కోరుకుంటున్నారు. A ఎంపిక కాగల సంభావ్యత 0.5, ఇద్దరూ ఎంపిక కాగల సంభావ్యత 0.3 అయితే, B ఎంపిక కాగల సంభావ్యత 0.9 అయ్యే అవకాశం ఉందా?
సాధన:
P(A) = 0.5; P(A ∩ B) = 0.3
∵ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ P(A ∪ B) = 0.5 + P(B) – 0.3
⇒ P(A ∪ B) = 0.2 + P(B) [∵ P(A ∪ B) ≤ 1]
⇒ 0.2 + P(B) ≤ 1
⇒ P(B) ≤ 0.8
కనుక P(B) = 0.9 కావడం అసాధ్యం.

ప్రశ్న 5.
ఒక కాంట్రాక్టరు రోడ్డు కాంట్రాక్టును పొందే సంభావ్యత \(\frac{2}{3}\), భవనం కాంట్రాక్టును పొందే సంభావ్యత \(\frac{5}{9}\), కనీసం ఒక కాంట్రాక్టునైనా పొందే సంభావ్యత \(\frac{4}{5}\). అతడు రెండు కాంట్రాక్టులనూ పొందే సంభావ్యతను కనుక్కోండి. [A.P. Mar. ’16]
సాధన:
కాంట్రాక్టరు రోడ్డు కాంట్రాక్టు పొందటానికి సంభావ్యత
P(A) = \(\frac{2}{3}\)
భవనం కాంట్రాక్టు పొందడానికి సంభావ్యత
P(B) = \(\frac{5}{9}\)
కనీసం ఒకటి పొందటానికి సంభావ్యత
P(A ∪ B) = \(\frac{4}{5}\)
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
రెండు కాంట్రాక్టులనూ పొందటానికి సంభావ్యత
∴ P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= \(\frac{2}{3}+\frac{5}{9}-\frac{4}{5}\)
= \(\frac{30+25-36}{45}\)
= \(\frac{19}{45}\)

ప్రశ్న 6.
25 మంది సభ్యులు గల ఒక కమిటీలో ప్రతి సభ్యుడు గణితంలో గానీ, సాంఖ్యక శాస్త్రంలో గానీ లేదా రెండింటిలో గానీ ప్రవీణులై ఉంటారు. వీరిలో 19 మంది గణితం లోనూ, 16 మంది సాంఖ్యకశాస్త్రంలోనూ ప్రవీణులైతే, కమిటీ నుంచి ఎంపిక చేసిన ఒక సభ్యుడు రెండింటిలోనూ ప్రవీణుడై ఉండే సంభావ్యతను కనుక్కోండి. [T.S. Mar. ’16]
సాధన:
ఎన్నుకొన్న వ్యక్తి గణితంలో ప్రవీణుడయ్యే ఘటన = M
సాంఖ్యకశాస్త్ర ప్రవీణుడయ్యే ఘటన = S అనుకుందాం.
P(M) = \(\frac{19}{25}\), P(S) = \(\frac{16}{25}\)
ప్రతివారూ ఏదో ఒక శాస్త్రంలో ప్రవీణులు.
∴ M ∪ S ఒక నిశ్చిత ఘటన, P(M ∪ S) = 1
సంభావ్యతల సంకలన సిద్ధాంతం నుండి
P(M ∪ S) = P(M) + P(S) – P(M ∩ S)
∴ P(M ∩ S) = \(\frac{19}{25}+\frac{16}{25}\) – 1
= \(\frac{35}{25}\) – 1
= \(\frac{10}{25}\)
= \(\frac{2}{5}\)
∴ ఎన్నుకొన్న వ్యక్తి రెండు శాస్త్రాల్లోనూ ప్రవీణుడయ్యే ఘటన సంభావ్యత = \(\frac{2}{5}\)

ప్రశ్న 7.
ఒక పరుగు పందెంలో A, B, C మూడు గుర్రాలు. A పందెం గెలిచే సంభావ్యత B సంభావ్యతకు రెట్టింపు, B పందెం గెలిచే సంభావ్యత C గెలుపుకి రెట్టింపు అయితే, A, B, C లు ఆ పందెం గెలవగల సంభావ్యతలేవి? [Mar. ’14, ’13]
సాధన:
ఇచ్చట A, B, C లు పరస్పర వివర్జిత ఘటనలు
P(A) + P(B) + P(C) = 1 ……(1)
దత్తాంశము నుంచి P(A) = 2P(B), P(B) = 2P(C) ……..(2)
(1), (2)ల నుంచి
2P(B) + P(B) + P(C) = 1
⇒ 3P(B) + P(C) = 1
⇒ 3 (2) P(C) + P(C) = 1
⇒ 7 P(C) = 1
⇒ P(C) = \(\frac{1}{7}\)
∴ P(C) = \(\frac{1}{7}\), P(B) = \(\frac{2}{7}\), P(A) = \(\frac{4}{7}\)

ప్రశ్న 8.
ఒక సంచిలో 12 రెండు రూపాయి నాణేలు, 7 రూపాయి నాణేలు, 4 అర్ధరూపాయి నాణేలు ఉన్నాయి. ఆ సంచి నుంచి యాదృచ్ఛికంగా మూడు నాణేలను ఎంపిక చేస్తే,
(i) మూడు నాణేల మొత్తం గరిష్టం కావడానికి
(ii) మూడు నాణేల మొత్తం కనిష్ఠం కావడానికి
(iii) మూడు నాణేలు వేర్వేరు విలువలను కలిగి ఉండటానికి గల సంభావ్యతలను కనుక్కోండి.
సాధన:
సంచిలోని నాణేల సంఖ్య = 12 + 7 + 4 = 23
వాటి నుండి యాదృచ్ఛికంగా 3 నాణేలను ఎన్నుకొనే విధాల సంఖ్య n(S) = ²³C₃
(i) E₁ అనేది ఎన్నుకున్న 3 నాణేల మొత్తం గరిష్టం కావడం అనే ఘటన అంటే మూడు రెండు రూపాయి నాణేలు కావాలి.
అందువలన n(E₁) = ¹²C₃
P(E₁) = \(\frac{n\left(E_1\right)}{n(S)}=\frac{{ }^{12} C_3}{{ }^{23} C_3}\)
(ii) E₂ అనేది ఎన్నుకున్న 3 నాణేల మొత్తం కనిష్టం కావడం అనే ఘటన అంటే మూడు నాణేలు అర్థరూపాయి నాణేలు కావాలి.
n(E₂) = ⁴C₃
P(E₂) = \(\frac{n\left(E_2\right)}{n(S)}=\frac{{ }^4 C_3}{{ }^{23} C_3}\)
(iii) E₃ అనేది ఒక్కొక్కటి ఒక్కో రకం నాణెం కావడం అనే ఘటన
n(E₃) = ¹²C₁ × ⁷C₁ × ⁴C₁ = 12 × 7 × 4
P(E₃) = \(\frac{n\left(E_3\right)}{n(S)}=\frac{12 \times 7 \times 4}{{ }^{23} C_3}\)

ప్రశ్న 9.
మూడు ఘటనలు A, B, C ల సంభావ్యతలు క్రింది విధంగా ఉన్నాయి.
P(A) = 0.3, P(B) = 0.4, P(C) = 0.8, P(A ∩ B) = 0.08, P (A ∩ C) = 0.28, P(A ∩ B ∩ C) = 0.09, P(A ∪ B ∪ C) ≥ 0.75. P(B ∩ C) అంతరం [0.23, 0.48] లో ఉంటుందని చూపండి.
సాధన:
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
⇒ P(A ∪ B ∪ C) = 0.3 + 0.4 + 0.8 – 0.08 – 0.28 – P(B ∩ C) + 0.09
= 1.59 – 0.36 – P(B ∩ C)
= 1.23 – P(B ∩ C)
దత్తాంశం నుంచి 0.75 ≤ P(A ∪ B ∪ C) ≤ 1
⇒ 0.75 ≤ 1.23 – P(B ∩ C) ≤ 1
⇒ -0.48 ≤ -P(B ∩ C) ≤ -0.23
⇒ 0.23 ≤ P(B ∩ C) ≤ 0.48
∴ P(B ∩ C) ∈ [0.23, 0.48]

ప్రశ్న 10.
మూడు పరస్పర వివర్జిత ఘటనల సంభావ్యతలు వరుసగా \(\frac{1+3 P}{3}, \frac{1-P}{4}, \frac{1-2 P}{2}\) అయితే \(\frac{-1}{3} \leq P \leq \frac{1}{2}\) అని నిరూపించండి.
సాధన:
ఇచ్చిన దత్తాంశం ప్రకారం,
∴ 0 ≤ \(\frac{1+3 P}{3}\) ≤ 1
⇒ 0 ≤ 1 + 3P ≤ 3
⇒ -1 ≤ 3P ≤ 2
⇒ \(\frac{-1}{3} \leq P \leq \frac{2}{3}\) ……….(1)
∴ 0 ≤ \(\frac{1-P}{4}\) ≤ 1
⇒ 0 ≤ 1 – P ≤ 4
⇒ -1 ≤ -P ≤ 3
⇒ 1 ≥ P ≥ -3
⇒ -3 ≤ P ≤ 1 …….(2)
∴ 0 ≤ \(\frac{1-2 P}{2}\) ≤ 1
⇒ 0 ≤ 1 – 2P ≤ 2
⇒ -1 ≤ -2P ≤ 1
⇒ 1 ≥ 2P ≥ -1
⇒ -1 ≤ 2P ≤ 1
⇒ \(\frac{-1}{2} \leq P \leq \frac{1}{2}\) ………(3)
(1), (2), (3) ల నుండి \(\frac{-1}{3} \leq P \leq \frac{1}{2}\)

ప్రశ్న 11.
ఒకడు పండుగరోజు A, B, C, D అనే 4 దేవాలయాలను యాధృచ్ఛిక క్రమంలో దర్శించుకోవాలనుకుంటాడు. అతడు (i) Bకి ముందుగా A (ii) B కి ముందుగా A మరియు Cకి ముందుగా B లను దర్శించుకొనే సంభావ్యతలను కనుక్కోండి.
సాధన:
(i) A, B, C, D లు కుర్చిలలో B కి ముందుగా A కూర్చొనే విధంగా దేవాలయాలు దర్శించుకొనుట, ముందుగా C, D లు 4 కుర్చీలలో కూర్చొనగల విధానాలు సంఖ్య ⁴P₂ = 12
మరియు మిగిలిన రెండు కుర్చీలలో B కి ముందుగా A కూర్చొనే విధానాల సంఖ్య 1.
n(S) = 24
B కి ముందుగా A దేవాలయం దర్శించుకొనే సంభావ్యత
B = \(\frac{12 \times 1}{24}=\frac{1}{2}\)
(i) మాదిరిగా ముందుగా D ను 4 కుర్చీలలో కూర్చొనగల విధానాల సంఖ్య 4.
మిగిలిన మూడు కుర్చీలలో Bకి ముందుగా A మరియు C కి ముందుగా B కూర్చొనగల విధానాల సంఖ్య.
n(S) = 4! = 24
∴ B కి ముందుగా A మరియు C కి ముందుగా B దేవాలయాలను దర్శించుకొనే సంభావ్యత = \(\frac{4 \times 1}{24}=\frac{1}{6}\)

ప్రశ్న 12.
ఒక కంపెనీలోని ఉద్యోగుల నుంచి 5 గురు వ్యక్తులను ఈ కంపెనీ పాలకవర్గ ప్రతినిధులుగా ఎన్నుకొన్నారు. 5గురు వ్యక్తుల వివరాలు క్రింది విధంగా వున్నాయి.

పై సమూహం నుంచి ఒక వ్యక్తిని యాధృచ్ఛికంగా ప్రసంగ కర్తగా ఎన్నుకొంటే, ఆ వ్యక్తి పురుషుడు లేదా 35 సంవత్సరాలు పైబడినవాడు అయ్యే సంభావ్యతను కనుక్కోండి.
సాధన:
5 గురు వ్యక్తులు గల పాలకవర్గం నుంచి యాదృచ్ఛికంగా ఒక వ్యక్తిని ఎన్నుకొంటే, ఎన్నుకొనే వ్యక్తి పురుషుడు అయ్యే ఘటనను A అని, మరియు 35 సంవత్సరములు దాటిన వ్యక్తి అయ్యే ఘటనను B అని మరియు శింపుల్ ఆవరణం S అనుకొనుము.
∴ n(S) = ⁵C₁ = 5
n(A) = ³C₁ = 3
P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{3}{5}\)
n(B) = ²C₁ = 2
P(B) = \(\frac{n(B)}{n(S)}\) = \(\frac{2}{5}\)
n(A ∩ B) = ¹C₁ = 1
P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}\) = \(\frac{1}{5}\)
సంభావ్యతపై సంకలన సిద్ధాంతంననుసరించి
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{3}{5}+\frac{2}{5}-\frac{1}{5}\)
= \(\frac{4}{5}\)

ప్రశ్న 13.
వందమందీ విద్యార్థుల నుంచి 40 మరియు 60 మంది విద్యార్ధులు గల రెండు సెక్షన్లు ఏర్పడ్డాయి. నీవు, నీ మిత్రుడు ఆవందమందిలో ఉండి
(i) మీ ఇద్దరూ ఒకే సెక్షన్లోకి ప్రవేశించే
(ii) వేర్వేరు సెక్షన్లలోకి ప్రవేశించే సంభావ్యతలను కనుక్కోండి.
సాధన:
S శాంపుల్ ఆవరణం అనుకొనుము.
n(S) = 100 మంది
విద్యార్థులను 40 మరియు 60 మంది విద్యార్థులుగా రెండు సెక్షన్లుగా గల విధానాల సంఖ్య = \(\frac{100 !}{40 ! 60 !}\)
(i) మీ ఇద్దరు ఒకే సెక్షన్లో ప్రవేశించే ముందుగా మీ ఇద్దరు మొదటి సెక్షన్లోకి ప్రవేశించగా మిగిలిన 98 మంది విద్యార్ధులను 38, 60 గా విభజించగల విధానాల సంఖ్య = \(\frac{98 !}{38 ! 60 !}\)
ఇదే విధంగా మీ ఇద్దరు రెండవ సెక్షన్లోకి ప్రవేశించగా మిగిలిన 98 మంది విద్యార్థులను 40, 58 గా విభజించగల విధానాల సంఖ్య

(ii) వేర్వేరు సెక్షన్లోకి ప్రవేశించే
∴ వేర్వేరు సెక్షన్లలోకి ప్రవేశించే సంభావ్యత = 1 – P(E)
= 1 – \(\frac{17}{33}\)
= \(\frac{16}{33}\)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 9 సంభావ్యత Exercise 9(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 9 సంభావ్యత Exercise 9(a)

అభ్యాసం – 9(ఎ)

I.

ప్రశ్న 1.
ఒక పాచికను దొర్లించే ప్రయోగంలో క్రింది ఘటనలు తీసుకొందాం.
A = {1, 3, 5}, B = {2, 4, 6}, C = { 1, 2, 3}
ఈ ఘటనలు సమసంభవాలేనా?
సాధన:
A, B, C ఘటనలు మూడింటిలో ఏ ఘటన సంభవమైనా, మిగతా ఘటనలు సంభవాని కంటే ఎక్కువగా సంభవించడానికి గల కారణం ఏమీ లేదు.
కనుక ఈ ఘటనలు సమసంభవ ఘటనలు.

ప్రశ్న 2.
ఒక పాచికను దొర్లించే ప్రయోగంలో క్రింది ఘటనలను తీసుకొందాం.
A = {1, 3, 5}, B = {2, 4}, C = {6}
ఈ ఘటనలు పరస్పర వివర్జితాలేనా?
సాధన:
A, B, C ఘటనలలో ఏ ఘటన సంభవమైనా, మిగతా ఘటనలలో మరోదాని సంభవాన్ని నిరోధిస్తుంది.
కనుక A, B, Cలు పరస్పర వివర్జిత ఘటనలు లేదా A ∩ B = φ, B ∩ C = φ, C ∩ A = φ
∴ A, B, C ఘటనలు పరస్పర వివర్జిత ఘటనలు.

ప్రశ్న 3.
ఒక పాచికను దొర్లించే ప్రయోగంలో క్రింది ఘటనలను తీసుకొందాం.
A = {2, 4, 6}, B = {3, 6}, C = {1, 5, 6}
ఈ ఘటనలు పూర్ణఘటనలేనా?
సాధన:
ఒక పాచికను దొర్లించే ప్రయోగంలో శాంపిల్ ఆవరణ
S = {1, 2, 3, 4, 5, 6}
∵ A ⊂ S, B ⊂ S, C ⊂ S మరియు
A ∪ B ∪ C = S
∴ A, B, C లు పూర్ణ ఘటనలు.

II.

ప్రశ్న 1.
పరస్పర వివర్ణిత, పూర్ణ ఘటనలకు రెండు ఉదాహరణలను ఇవ్వండి.
సాధన:
(i) ఒక పాచికను దొర్లించే యాదృచ్ఛిక ప్రయోగంలో శాంపిల్ ఆవరణ S = {1, 2, 3, 4, 5, 6).
E₁ అనేది పాచికను దొర్లించినపుడు బేసి అంకెరావటం అనే ఘటన
E₁ = {1, 3, 5}
E₂ అనేది పాచికను దొర్లించినప్పుడు సరిఅంకె రావటం అనే ఘటన
E₂ = {2, 4, 6}
అప్పుడు E₁ ⊂ S, E₂ ⊂ S మరియు E₁ ∪ E₂ = S, E₁ ∩ E₂ = φ
∴ E₁, E₂ లు పరస్పర వివర్జిత, పూర్ణ ఘటనలు.

(ii) రెండు నాణేలను ఒకేసారి దొర్లించే యాదృచ్ఛిక ప్రయోగంలో శాంపిల్ ఆవరణ
S = {HH, HT, TH, TT}
(H బొమ్మను, T అచ్చును సూచిస్తుంది)
E₁ అనేది రెండు నాణేలను ఒకేసారి దొర్లించినపుడు కనీసం ఒక బొమ్మ రావటం అనే ఘటన
∴ E₁ = {HH, HT, TH}
E₂ అనేది రెండు నాణేలను ఒకేసారి దొర్లించినపుడు రెండూ అచ్చులు కావటం అనే ఘటన
∴ E₂ = {TT}
∵ E₁ ⊂ S, E₂ ⊂ S, E₁ ∪ E₂ = S మరియు E₁ ∩ E₂ = φ
∴ E₁, E₂ లు పరస్పర వివర్జిత, పూర్ణ ఘటనలు.

ప్రశ్న 2.
పరస్పర వివర్జిత ఘటన గానీ, పూర్ణ ఘటన గానీ కానట్టి ఘటనలకు రెండు ఉదాహరణలను ఇవ్వండి.
సాధన:
(i) ఒక పాచికను దొర్లించే యాదృచ్ఛిక ప్రయోగంలో E₁ అనేది సరి ప్రధాన సంఖ్య రావటం అనే ఘటన, E₂ అనేది సరిసంఖ్య రావటం అనే ఘటన అనుకుంటే,
S = {1, 2, 3, 4, 5, 6}, E₁ = {2}, E₂ = {2, 4, 6}
E₁ ∩ E₂ = {2} ≠ φ, E₁ ∪ E₂ = {2, 4, 6} ⊂ S
కనుక E₁, E₂ లు రెండు పరస్పర వివర్జితం గానీ, పూర్ణ ఘటనలు గానీ కానటువంటి ఘటనలు.

(ii) రెండు నాణేలను దొర్లించినపుడు ఒక బొమ్మ రావటం అనేది ఘటన E₁, కనీసం ఒక బొమ్మ రావటం అనేది E₂ అనుకుంటే
S = {HH, HT, TH, TT}
E₁ = {HT, TH}
E₂ = {HH, HT, TH}
ఇచ్చట E₁ ∩ E₂ = {(H, T), (T, H)} ≠ φ
E₁ ∪ E₂ = {(H, H), (H, T), (T, H)} ⊂ S
∴ E₁, E₂ లు పరస్పర వివర్జితం గానీ, పూర్ణ ఘటనలు గానీ కానటువంటి ఘటనలు.

ప్రశ్న 3.
సమసంభవాలు గానీ, పూర్ణ ఘటనగానీ కానటువంటి ఘటనలకు రెండు ఉదాహరణలిమ్ము.
సాధన:
(i) రెండు నాణేలను ఎగురవేసే యాదృచ్ఛిక ప్రయోగంలో E₁ అనేది ఒక బొరుసు రావటం అనే ఘటన E₂ అనేది కనీసం ఒక ‘బొరుసు’ రావటం అనే ఘటన అనుకుంటే,
శాంపిల్ ఆవరణ
S = {HH, HT, TH, TT}
E₁ = {HT, TH}
E₂ = {HT, TH, TT}
P(E₁) = \(\frac{2}{4}=\frac{1}{2}\), P(E2) = \(\frac{3}{4}\)
∵ P(E₁) ≠ P(E₂)
E₁, E₂ లు సమసంభవాలు కానీ ఘటనలు.
E₁ ∪ E₂ = {HT, TH, TT} ⊂ S
∴ E₁, E₂ లు పూర్ణ ఘటనలు కావు.

(ii) పాచికను దొర్లించే యాదృచ్ఛిక ప్రయోగంలో
E₁ అనేది బేసి ప్రధాన సంఖ్య రావటం అనే ఘటనను, E₂ అనేది బేసి సంఖ్య రావటం అనే ఘటన అనుకుంటే,
S = {1, 2, 3, 4, 5, 6}, E₁ = {3, 5}, E₂ = {1, 3, 5}
P(E₁) = \(\frac{2}{6}\), P(E₂) = \(\frac{3}{6}\)
∵ P(E₁) ≠ P(E₂)
∴ E₁, E₂ లు సమసంభవాలు కానీ ఘటనలు
E₁ ∪ E₂ = {1, 3, 5) ⊂ S
∴ E₁, E₂ లు పూర్ణ ఘటనలు కావు.

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 8 విస్తరణ కొలతలు Exercise 8(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 8 విస్తరణ కొలతలు Exercise 8(a)

అభ్యాసం – 8(ఎ)

I.

ప్రశ్న 1.
క్రింది దత్తాంశానికి మధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుక్కోండి.
(i) 38, 70, 48, 40, 42, 55, 63, 46, 54, 44
సాధన:
దత్తాంశానికి అంకమధ్యమము
\(\bar{x}=\frac{38+70+48+40+42+55+63+46+54+44}{10}\)
= \(\frac{500}{10}\)
= 50
విచలనాల పరమ మూల్యాలు \(\left|x_i-\bar{x}\right|\)
|50 – 38|, |50 – 70|, |50 – 48|, |50 – 40|, |50 – 42|, |50 – 55|, |50 – 63|, |50 – 46|, |50 – 54|, |50 – 44|
= 12, +20, 2, 10, 8, +5, +13, 4, +4, 6
∴ మధ్యమం నుంచి మధ్యమ విచలనం = \(\frac{\sum_{i=1}^{10}\left|x_i-\bar{x}\right|}{10}\)
= \(\frac{12+20+2+10+8+5+13+4+4+6}{10}\)
= \(\frac{84}{10}\)
= 8.4

(ii) 3, 6, 10, 4, 9, 10
సాధన:
దత్తాంశానికి అంకమధ్యమము
\(\bar{x}=\frac{3+6+10+4+9+10}{6}\)
= \(\frac{42}{6}\)
= 7
విచలనాల పరమ మూల్యాలు \(\left|x_i-\bar{x}\right|\)
|3 – 7|, |16 – 7|, |10 – 7|, |4 – 7|, |9 – 7|, |10 – 7|
= 14, 1, 3, 3, 2, 3
∴ మధ్యమం నుంచి మధ్యమ విచలనం = \(\frac{\sum_{i=1}^6\left|x_i-\bar{x}\right|}{6}\)
= \(\frac{4+1+3+3+2+3}{6}\)
= \(\frac{16}{6}\)
= 2.666

ప్రశ్న 2.
క్రింది దత్తాంశానికి మధ్యగతం నుంచి మధ్యమ విచలనాన్ని కనుక్కోండి. [A.P. Mar. ’16]
(i) 13, 17, 16, 11, 13, 10, 16, 11, 18, 12, 17
సాధన:
అవర్గీకృత దత్తబిందువులు
13, 17, 16, 11, 13, 10, 16, 11, 18, 12, 17
దత్తబిందువులను పరిమాణం పరంగా ఆరోహణక్రమంలో వ్రాయగా
10, 11, 11, 12, 13, 13, 16, 16, 17, 17, 18
∴ మధ్యగతం = 13 = b (అనుకొనిన)
పరమ మూల్య విలువలు
|13 – 10|, |13 – 11|, |13 – 11|, |13 – 12|, |13 – 13|, |13 – 13|, |13 – 16|, |13 – 16|, |13 – 17|, |13 – 17|, |13 – 18|
= 3, 2, 2, 1, 0, 0, 3, 3, 4, 4, 5
∴ మధ్యగతం నుంచి మధ్యమ విచలనం = \(\frac{\sum_{i=1}^{11}\left|x_i-b\right|}{11}\)
= \(\frac{3+2+2+1+0+0+3+3+4+4+5}{11}\)
= \(\frac{27}{11}\)
= 2.45

(ii) 4, 6, 9, 3, 10, 13, 2
సాధన:
అవర్గీకృత దత్తబిందువులు
4, 6, 9, 3, 10, 13, 2
దత్తబిందువులను పరిమాణం పరంగా ఆరోహణక్రమంలో వ్రాయంగా
2, 3, 4, 6, 9, 10, 13
∴ మధ్యగతం = 6 = b (అనుకొనిన)
పరమ మూల్య విలువలు
|6 – 2|, |6 – 3|, |6 – 4|, |6 – 6|, |6 – 9|, |6 – 10|, |6 – 13|
= 4, 3, 2, 0, 3, 4, 7
∴ మధ్యగతం నుంచి మధ్యమ విచలనం = \(\frac{\sum_{i=1}^7\left|x_i-b\right|}{7}\)
= \(\frac{4+3+2+0+3+4+7}{7}\)
= 3.285

ప్రశ్న 3.
క్రింది విభాజనానికి మధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుక్కోండి.
(i)

సాధన:
పట్టికను నిర్మిద్దాం

(ii)

సాధన:
పట్టికను నిర్మిద్దాం

ప్రశ్న 4.
క్రింది పౌనఃపున్య విభాజనానికి మధ్యగతం నుంచి మధ్యమవిచలనాన్ని కనుక్కోండి.

సాధన:

\(\frac{N}{2}\) = 13
∴ మధ్యగతం = 7
మధ్యగతం నుంచి మధ్యమ విచలనం = \(\frac{1}{N}\) Σf_i |x_i – మధ్యగతం|
= \(\frac{1}{26}\) (84)
= 3.23

II.

ప్రశ్న 1.
(i) క్రింది అవిచ్ఛిన్న విభాజనాలకు మధ్యగతం నుంచి మధ్యమ విచలనాన్ని కనుక్కోండి.

సాధన:
పట్టికను నిర్మిద్దాం

\(\frac{N}{2}\) = 25 వ పరిశీలన, 20-30 తరగతి అంతరంలో ఉన్నది.
ఇదే మధ్యగత తరగతి
∴ మధ్యగతం = \(L+\left\{\frac{\frac{N}{2}-P \cdot C \cdot f}{f}\right\}i\)
= 20 + \(\left\{\frac{25-14}{14}\right\} 10\)
= 20 + 7.857
= 27.857
∴ మధ్యగతం నుంచి మధ్యమ విచలనం = \(\frac{1}{N} \sum_{i=1}^6 f_1 \mid x_i\) – మధ్యగతం|
= \(\frac{1}{50}\) (517.1)
= 10.34

(ii)

సాధన:
\(\frac{\mathrm{N}}{2}=\frac{100}{2}\) = 50వ పరిశీలన, 40-50 తరగతి అంతరంలో ఉన్నది.
ఇదే మధ్యగత తరగతి
∴ మధ్యగతం = \(L+\left\{\frac{\frac{N}{2}-P \cdot C \cdot f}{f}\right\} \times i\)
= 40 + \(\left\{\frac{50-32}{28}\right\} \times 10\)
= 40 + 6.43
= 46.43
పట్టికను నిర్మిద్దాం

∴ మధ్యగతం నుంచి మధ్యమ విచలనం = \(\frac{1}{N} \sum_{i=1}^8 f_i \mid x_i\) – మధ్యగతం|
= \(\frac{1}{100}\) (1428.6)
= 14.286

ప్రశ్న 2.
క్రింది అవిచ్ఛిన్న విభాజనానికి మధ్యమం నుంచి మధ్యమ విచలనాన్ని కనుక్కోండి.

సాధన:
ఊహత్మక మధ్యమం a = 130 మరియు h = 10
పట్టికను నిర్మిద్దాం

\(\bar{x}=a+\left(\frac{\sum f_i d_i}{N}\right) h\)
= 130 + \(\left(\frac{-47}{100}\right) 10\)
= 130 – 4.7
= 125.3
మధ్యమం నుంచి మధ్యమ విచలనం = \(\frac{1}{N} \sum_{i=1}^6 f_i\left|x_i-\bar{x}\right|\)
= \(\frac{1}{100}\) (1428.8)
= 14.288

ప్రశ్న 3.
క్రింది ఇచ్చిన విచ్ఛిన్న దత్తాంశానికి విస్తృతిని కనుక్కోండి.
(i) 6, 7, 10, 12, 13, 4, 8, 12
సాధన:
ఇచ్చిన విచ్ఛిన్న దత్తాంశం 6, 7, 10, 12, 13, 4, 8, 12
మధ్యమం \(\overline{\mathrm{x}}=\frac{6+7+10+12+13+4+8+12}{8}\)
= \(\frac{72}{8}\)
= 9
పట్టికను నిర్మిద్దాం

విస్తృతి σ² = \(\frac{1}{n} \sum\left(x_i-\bar{x}\right)^2\)
= \(\frac{1}{8}\) (74)
= 9.25

(ii) 350, 361, 370, 373, 376, 379, 385, 387, 394, 395
సాధన:
ఇచ్చిన విచ్ఛిన్న దత్తాంశం 350, 361, 370, 373, 376, 379, 385, 387, 394, 395
మధ్యమం \(\bar{x}=\frac{350+361+370+373+376+379+385+387+394+395}{10}\) = 377
పట్టికను నిర్మిద్దాం

విస్తృతి σ² = \(\frac{1}{n} \sum_{i=1}^{10}\left(x_i-\bar{x}\right)^2\)
= \(\frac{1}{10}\) (1832)
= 183.2

ప్రశ్న 4.
క్రింది పౌనఃపున్య విభాజనానికి విస్తృతి, ప్రామాణిక విచలనాలను కనుక్కోండి.

సాధన:
పట్టికను నిర్మిద్దాం

\(\bar{x}=\frac{\sum f_i x_i}{N}=\frac{760}{40}=19\)
విస్తృతి σ² = \(\frac{1}{N} \sum_{i=1}^7 f_i\left(x_i-\bar{x}\right)^2\)
= \(\frac{1}{40}\) (1736)
= 43.4
∴ ప్రామాణిక విచలనం σ = \(\sqrt{43.4}\) = 6.59

III.

ప్రశ్న 1.
542 సభ్యుల వయస్సు విభాజనం తెలిపే క్రింది పట్టికలోని దత్తాంశానికి సోపాన విచలన పద్ధతినుపయోగించి మధ్యమాన్ని, విస్తృతిని కనుక్కోండి.

సాధన:
ఊహత్మక మధ్యమం A = 55 మరియు h = 10
అపుడు y_i = \(\frac{x_i-55}{10}\)
పట్టికను నిర్మిద్దాం

మధ్యమం \(\bar{x}=A+\left(\frac{\sum f_i y_i}{N}\right) h\)
= 55 + \(\left(\frac{-15}{542}\right) 10\)
= 55 – 0.277
= 54.723 సం॥
విస్తృతి σ² = \(\frac{h^2}{N^2}\left[N \sum f_i y_i^2-\left(\sum f_i y_i\right)^2\right]\)
= \(\frac{100}{(542)^2}\) [542(765) – (-15)²]
= \(\frac{100}{293764}\) [414630 – 225]
= \(\frac{100}{293764}\) (414405)
= 141.07 సం॥

ప్రశ్న 2.
రెండు విభాజనాల విచలనాంకాలు 60, 70 వాటి ప్రామాణిక విచలనాలు వరసగా 21, 16 వాటి అంకమధ్యమాలను కనుక్కోండి.
సాధన:
ఇచ్చిన విభాజనాల విచలనాంకం C.V = 60
ప్రామాణిక విచలనం σ = 21
విచలనాంకం = \(\frac{\sigma}{\bar{x}} \times 100\)
⇒ \(\bar{x}=\frac{\sigma}{C . V} \times 100\) = \(\frac{21}{60}\) × 100
అంకమధ్యమం = 35
ఇచ్చిన విభాజనాల విచలనాంకం C.V = 70
ప్రామాణిక విచలనం = 16
విచలనాంకం = \(\frac{\sigma}{\bar{x}} \times 100\)
⇒ \(\bar{x}=\frac{\sigma}{C . V} \times 100\)
= \(\frac{16}{70}\) × 100
= 22.85

ప్రశ్న 3.
10 రోజులపాటు జరిగిన వర్తకంలో క్రింది ఇచ్చిన X, Y వాటాల (షేరుల) ధరల నుంచి, ఏ షేరు (వాటా) ఎక్కువ నిలకడ కలిగినదో కనుక్కోండి.

సాధన:
X వాటాల మధ్యమం
\(\bar{x}=\frac{35+54+52+53+56+58+52+50+51+49}{10}=\frac{510}{10}\) = 51
Y వాటాల మధ్యమం
\(\bar{y}=\frac{108+107+105+105+106+107+104+103+104+101}{10}\)
= \(\frac{1050}{10}\)
= 105

X వాటాల ప్రామాణిక విచలనం = σ_x = \(\sqrt{\frac{1}{n} \Sigma\left(x_i-\bar{x}\right)^2}\)
= \(\sqrt{\frac{1}{10}(350)}\)
= 5.92
Y వాటాల ప్రామాణిక విచలనం = σ_y = \(\sqrt{\frac{1}{n} \sum\left(y_i-\bar{y}\right)^2}\)
= \(\sqrt{\frac{1}{10}(40)}\)
= 2
X వాటాల విచలనాంకం = \(\frac{\sigma_x}{\bar{x}} \times 100\)
= \(\frac{5.92}{51}\) × 100
= 11.61
Y వాటాల విచలనాంకం = \(\frac{\sigma_y}{\bar{y}} \times 100\)
= \(\frac{2}{105}\) × 100
= 1.91
\(\bar{x}<\bar{y}\) మరియు X వాటాల విచలనాంకం > Y వాటాల విచలనాంకం కావున
∴ Y షేరు (వాటా) ఎక్కువ నిలకడ కలిగి ఉన్నది.

ప్రశ్న 4.
5 పరిశీలనల మధ్యమం 4.4. వాటి నిస్తృతి 8.24. వాటిలో మూడు పరిశీలనలు 1, 2, 6 అయితే మిగిలిన రెండు పరిశీలనలను కనుక్కోండి.
సాధన:
కావలసిన రెండు పరిశీలనలు x, y అనుకొనుము.
దత్తాంశాల నుండి 5 పరిశీలనల మధ్యమం 4.4
⇒ \(\frac{1+2+6+x+y}{5}\) = 4.4
⇒ 9 + x + y = 22
⇒ x + y = 13 ……..(1)
5 పరిశీలనల విస్తృతి = 8.24
⇒ \(\frac{1}{5}\) [(1 – 4.4)² + (2 – 4.4)² + (6 – 4.4)² + (x – 4.4)² + (y – 4.4)²] = 8.24
⇒ (-3.4)² + (-2.4)² + (1.6)² + x² – 8.8x + 19.36 + y² – 8.8y + 19.36 = 41.2
⇒ x² + y² – (8.8) (x + y) = 41.2 – 11.56 – 5.76 – 2.56 – 19.36 – 19.36
⇒ x² + y² – (8.8) (13) = -17.4
⇒ x² + y² = -17.4 + 114.4
⇒ x² + y² = 97
(x + y)² = x² + y² + 2xy
⇒ 169 = 97 + 2xy
⇒ 2xy = 72
⇒ xy = 36
(x – y)² = (x + y)² – 4xy
= 169 – 144
= 25
⇒ x – y = 5 …….(2)
(1) + (2) ⇒ 2x = 18
⇒ x = 9
(1) – (2) ⇒ 2y = 8
⇒ y = 4
∴ కావలసిన మిగిలిన రెండు పరిశీలనలు 4, 9.

ప్రశ్న 5.
9 అంశాలు కలిగిన ఒక సమితి యొక్క అంకమధ్యమం, ప్రామాణిక విచలనాలు వరసగా 43, 5. ఈ సమితికి 63 విలువ గల ఒక అంశం చేర్చితే, ఇచ్చిన 10 అంశాల సమితికి కొత్త మధ్యమం, ప్రామాణిక విచలనాన్ని కనుక్కోండి.
సాధన:
దత్తాంశం నుండి 9 అంశాల అంకమధ్యమం = 43
∴ \(\bar{x}=\frac{1}{9} \sum_{i=1}^9 x_i\) = 43
⇒ Σx_i = 387
9 అంశాలు కలిగిన సమితికి 63 విలువగల ఒక అంశం చేర్చగా
Σy_i = Σx_i + 63
= 387 + 63
= 450
∴ \(\frac{1}{10} \sum y_i\) = \(\frac{1}{10}\) (450) = 45
∴ కొత్త మధ్యమం = 45
దత్తాంశం నుండి 9 అంశాల ప్రామాణిక విచలనం = 5
⇒ σ = 5
⇒ σ² = 25
⇒ \(\frac{1}{9} \sum_{i=1}^9\left(x_i-\bar{x}\right)^2\) = 5
⇒ \(\sum_{i=1}^9\left(x_i-43\right)^2\) = 225 …….(1)
కొత్త విస్తృతి σ² = \(\frac{1}{10} \sum_{i=1}^{10}\left(y_i-45\right)^2\)
= \(\frac{1}{10}\) [(x₁ – 45)² + (x₂ – 45)² + …….. + (x₉ – 45)² + (63 – 45)²]
మొదట 9 అంశాలు ఒకే రకం i.e, x_i = y_i, i = 1, 2, 3, …., 9
= \(\frac{1}{10}\) [(x₁ – 43 – 2)² + (x₂ – 43 – 2)² + ……. + (x₉ – 43 – 2)² + 324]
= \(\frac{1}{10}\) [(x₁ – 43)² + 4 – 2 . 2 . (x₁ – 43) + (x₂ – 43)² + 4 – 2 . 2 . (x₂ – 43) + …. + (x₉ – 43)² + 4 – 2 . 2 . (x₉ – 43) + 324]
= \(\frac{1}{10}\) [(x₁ – 43)² + (x₂ – 43)² + …… + (x₉ – 43)² + 36 – 4{x₁ – 43 + x₂ – 43 ….. + x₉ – 43} + 324]
= \(\frac{1}{10}\) [225 + 36 – 4(x₁ + x₂ + ……. + x₉ – 387) + 324]
= \(\frac{1}{10}\) [225 + 36 – 4(387 – 387) + 324]
= \(\frac{1}{10}\) [585]
= 58.5
కొత్త ప్రామాణిక విచలనం σ = \(\sqrt{58.5}\) = 7.65

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(d) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(d)

అభ్యాసం – 7(డి)

ప్రశ్న 1.
\(\frac{5 x+6}{(2+x)(1-x)}\) ను x లో ఘాతశ్రేణిగా విస్తరించ గలిగే ప్రదేశాన్ని తెలుపుతూ, x³ గుణకాన్ని కనుక్కోండి.
సాధన:
\(\frac{5 x+6}{(2+x)(1-x)}=\frac{A}{2+x}+\frac{B}{1-x}\) అనుకుందాం.
5x + 6 = A(1 – x) + B(2 + x)
x = 1 ⇒ 11 = B(2 + 1)
⇒ 11 = 3B
⇒ B = \(\frac{11}{3}\)
x = -2 ⇒ -4 = A(1 + 2)
⇒ -4 = 3A
⇒ A = \(-\frac{4}{3}\)
∴ A = \(-\frac{4}{3}\), B = \(\frac{11}{3}\)

ప్రశ్న 2.
\(\frac{3 x^2+2 x}{\left(x^2+2\right)(x-3)}\) ను x లో ఘాతశ్రేణిగా విస్తరించ గలిగే అంతరాన్ని తెలుపుతూ x⁴ గుణకాన్ని కనుక్కోండి.
సాధన:
\(\frac{3 x^2+2 x}{\left(x^2+2\right)(x-3)}=\frac{A}{x-3}+\frac{B x+C}{x^2+2}\) అనుకుందాం.
3x² + 2x = A(x² + 2) + (Bx + C) (x – 3) ….(1)
x = 3 వ్రాస్తే, 27+ 6 = A(9 + 2)
⇒ 33 = 11A
⇒ A = 3
(1) లో x² గుణకాలను పోల్చగా
3 = A + B
⇒ B = 3 – A
= 3 – 3
= 0
(1) లో స్థిరపదాలను పోల్చగా
2A – 3C = 0
⇒ 3C = 2A
⇒ 3C = 6
⇒ C = 2
∴ A = 3, B = 0, C = 2

ప్రశ్న 3.
\(\frac{x-4}{x^2-5 x+6}\) ను x లో ఘాతశ్రేణిగా విస్తరించగలిగే ప్రదేశాన్ని తెలుపుతూ, xⁿ గుణకాన్ని కనుక్కోండి.
సాధన:
\(\frac{x-4}{x^2-5 x+6}=\frac{A}{x-2}+\frac{B}{x-3}\) అనుకుందాం.
x – 4 = A(x – 3) + B(x – 2) ……(1)
x = 2 వ్రాస్తే, -2 = A(2 – 3)
⇒ -2 = -A
⇒ A = 2
x = 3 వ్రాస్తే, -1 = B(3 – 2)
⇒ -1 = B
⇒ B = -1
∴ A = 2, B = -1

ప్రశ్న 4.
\(\frac{3 x}{(x-1)(x-2)^2}\) ను x లో ఘాతశ్రేణిగా విస్తరించగలిగే ప్రదేశాన్ని తెలుపుతూ xⁿ గుణకాన్ని కనుక్కోండి.
సాధన:
\(\frac{3 x}{(x-1)(x-2)^2}\) = \(\frac{A}{x-1}+\frac{B}{x-2}+\frac{C}{(x-2)^2}\) అనుకొనుము.
= \(\frac{A(x-2)^2+B(x-1)(x-2)+C(x-1)}{(x-1)(x-2)^2}\)
∴ 3x = A(x – 2)² + B(x – 1) (x – 2)+ c(x – 1) ……(1)
x = 1 వ్రాస్తే, 3 = A(1 – 2)²
⇒ A = 3
x = 2 వ్రాస్తే, 6 = C(2 – 1)
⇒ C = 6
(1) లో x² గుణకాలను పోల్చగా
0 = A + B
⇒ B = -A
⇒ B = -3
∴ A = 3, B = -3, C = 6

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(c) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(c)

అభ్యాసం – 7(సి)

క్రింది భిన్నాలను పాక్షిక భిన్నాలుగా విడగొట్టండి.

ప్రశ్న 1.
\(\frac{x^2}{(x-1)(x-2)}\)
సాధన:
\(\frac{x^2}{(x-1)(x-2)}=1+\frac{A}{x-1}+\frac{B}{x-2}\) అనుకుందాం.
x² = (x – 1) (x – 2) + A(x – 2) + B(x – 1)
x = 1 వ్రాస్తే, 1 = A(-1) ⇒ A = -1
x = 2 వ్రాస్తే, 4 = B(1) ⇒ B = 4
∴ A = -1, B = 4
∴ \(\frac{x^2}{(x-1)(x-2)}=1-\frac{1}{x-1}+\frac{4}{x-2}\)

ప్రశ్న 2.
\(\frac{x^3}{(x-1)(x+2)}\)
సాధన:

ప్రశ్న 3.
\(\frac{x^3}{(2 x-1)(x-1)^2}\)
సాధన:
\(\frac{x^3}{(2 x-1)(x-1)^2}\) = \(\frac{1}{2}+\frac{A}{2 x-1}+\frac{B}{x-1}+\frac{C}{(x-1)^2}\) అనుకుందాం.
2x³ = (2x – 1) (x – 1)² + 2A(x – 1)² + 2B(2x – 1) (x – 1) + 2C(2x – 1)
x = \(\frac{1}{2}\) వ్రాస్తే, 2(\(\frac{1}{8}\)) = 2A(\(\frac{1}{4}\))
⇒ A = \(\frac{1}{2}\)
x = 1 వ్రాస్తే, 2(1) = 2C(1)
⇒ C = 1
x = 0 వ్రాస్తే, 0 = (-1) (1) + 2A(1) + 2B(-1) (-1) + 2C(-1)
⇒ 2A + 2B – 2C = 1
⇒ 2B = 1 + 2C – 2A
⇒ 2B = 1 + 2 – 1
⇒ 2B = 2
⇒ B = 1
∴ A = \(\frac{1}{2}\), B = 1, C = 1
∴ \(\frac{x^3}{(2 x-1)(x-1)^2}\) = \(\frac{1}{2}+\frac{1}{2(2 x-1)}+\frac{1}{(x-1)}+\frac{1}{(x-1)^2}\)

ప్రశ్న 4.
\(\frac{x^3}{(x-a)(x-b)(x-c)}\)
సాధన:
\(\frac{x^3}{(x-a)(x-b)(x-c)}\) = \(1+\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c}\) అనుకోండి.
(x – a)(x – b)(x – c) చే గుణించగా
x³ = (x – a)(x – b)(x – c) + A(x – b) (x – c) + B(x – a) (x – c) + C(x – a) (x – b)
x = a ⇒ a³ = A(a – b) (a – c)
⇒ A = \(\frac{a^3}{(a-b)(a-c)}\)
x = b ⇒ b³ = B(b – a) (b – c)
⇒ B = \(\frac{b^3}{(b-a)(b-c)}\)
x = c ⇒ c³ = C(c – a) (c – b)
⇒ C = \(\frac{c^3}{(c-a)(c-b)}\)
∴ \(\frac{x^3}{(x-a)(x-b)(x-c)}\) = \(1+\frac{a^3}{(a-b)(a-c)(x-a)}+\frac{b^3}{(b-a)(b-c)(x-b)}\) + \(\frac{c^3}{(c-a)(c-b)(x-c)}\)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(b)

అభ్యాసం – 7 (బి)

క్రింది భిన్నాలను పాక్షిక భిన్నాలుగా విడగొట్టండి.

ప్రశ్న 1.
\(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}\) [May, Mar. ’11]
సాధన:
\(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+2}\) అనుకుందాం.
2x² + 3x + 4 = A(x² + 2) + (Bx + C) (x – 1) …….(1)
x = 1 వ్రాస్తే, 2 + 3 + 4 = A(1 + 2)
⇒ 9 = 3A
⇒ A = 3
(1) లో x² గుణకాలను పోల్చగా
2 = A + B
⇒ B = 2 – A
⇒ B = 2 – 3
⇒ B = -1
(1) లో స్థిరపదాలను పోల్చగా
4 = 2A – C
⇒ C = 2A – 4
= 6 – 4
= 2
∴ A = 3, B = -1, C = 2
\(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{3}{x-1}+\frac{-x+2}{x^2+2}\)

ప్రశ్న 2.
\(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}\)
సాధన:
\(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}=\frac{A}{2+x}+\frac{B x+C}{1-x+x^2}\) అనుకుందాం.
3x – 1 = A(1 – x + x²) (Bx + C) (2 + x) …….(1)
x = -2 వ్రాస్తే, -7 = A(1 + 2 + 4)
⇒ -7 = 7A
⇒ A = -1
(1) లో x² గుణకాలను పోల్చగా
0 = A + B
⇒ B = -A = 1
స్థిరపదాలను పోల్చగా
-1 = A + 2C
⇒ 2C = -1 – A
⇒ 2C = -1 + 1
⇒ 2C = 0
⇒ C = 0
∴ A = -1, B = 1, C = 0
\(\frac{3 x-1}{\left(1-x+x^2\right)(2+x)}=-\frac{1}{2+x}+\frac{x}{1-x+x^2}\)

ప్రశ్న 3.
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}\)
సాధన:
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{A}{x+2}+\frac{B x+C}{x^2+1}\) అనుకుందాం.
x² – 3 = A(x² + 1) + (Bx + C) (x + 2) …..(1)
x = -2 వ్రాస్తే, 4 – 3 = A(4 + 1)
⇒ 1 = 5A
⇒ A = \(\frac{1}{5}\)
(1) లో x² గుణకాలను పోల్చగా
1 = A + B
⇒ B = 1 – A
⇒ B = 1 – \(\frac{1}{5}\)
⇒ B = \(\frac{4}{5}\)
(1) లో స్థిరపదాలను పోల్చగా
-3 = A + 2C
⇒ 2C = -3 – A
⇒ 2C = -3 – \(\frac{1}{5}\)
⇒ 2C = \(-\frac{16}{5}\)
⇒ C = \(-\frac{8}{5}\)
∴ A = \(\frac{1}{5}\), B = \(\frac{4}{5}\), C = \(-\frac{8}{5}\)
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{1}{5(x+2)}+\frac{4 x-8}{5\left(x^2+1\right)}\)

ప్రశ్న 4.
\(\frac{x^2+1}{\left(x^2+x+1\right)^2}\)
సాధన:
\(\frac{x^2+1}{\left(x^2+x+1\right)^2}=\frac{A x+B}{x^2+x+1}+\frac{C x+D}{\left(x^2+x+1\right)^2}\) అనుకుందాం.
x² + 1 = (Ax + B) (x² + x + 1) + (Cx + D) ……(1)
(1) లో x³ గుణకాలను పోల్చగా, A = 0
(1) లో x² గుణకాలను పోల్చగా, A + B = 1 ⇒ B = 1
(1) లో x గుణకాలను పోల్చగా, A + B + C = 0
⇒ 1 + C = 0
⇒ C = -1
(1) లో స్థిరపదాలను పోల్చగా, B + D = 1
⇒ D = 1 – B
= 1 – 1
= 0
∴ A = 0, B = 1, C = -1, D = 0
∴ Ax + B = 1, Cx + D = -x
∴ \(\frac{x^2+1}{\left(x^2+x+1\right)^2}=\frac{1}{x^2+x+1}-\frac{x}{\left(x^2+x+1\right)^2}\)

ప్రశ్న 5.
\(\frac{x^3+x^2+1}{(x-1)\left(x^3-1\right)}\)
సాధన:

∴ x³ + x² + 1 = A(x – 1) (x² + x + 1) + B(x² + x + 1) + (Cx + D) (x – 1)² ……(2)
x = 1 ను (2) లో వ్రాయగా
1 + 1 + 1 = A(0) + B(1 + 1 + 1) + (C(1) + D) (0)
⇒ 3B = 3
⇒ B = 1
(2) లో x³ గుణకాలను పోల్చగా
1 = A + C ….(3)
(2) లో x² గుణకాలను పోల్చగా
1 = A(1 – 1) + B(1) + C(-2) + D(1)
⇒ 1 = B – 2C + D
⇒ 1 = 1 – 2C + D
⇒ 2C = D ……..(4)
x = 0 ను (2) లో వ్రాయగా
1 = A(-1) (1) + B(1) + D(-1)²
⇒ A + B + D = 1
⇒ -A + 1 + D = 1
⇒ A = D ……..(5)
(3), (4), (5) ల నుండి
1 = D + \(\frac{D}{2}\)
⇒ \(\frac{3D}{2}\) = 1
⇒ D = \(\frac{2}{3}\)
(5) నుండి A = \(\frac{2}{3}\)
(4) నుండి C = \(\frac{\mathrm{D}}{2}=\frac{\left(\frac{2}{3}\right)}{2}=\frac{1}{3}\)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(a)

అభ్యాసం – 7(ఎ)

I. క్రింది భిన్నాలను పాక్షిక భిన్నాలుగా విడగొట్టండి.

ప్రశ్న 1.
\(\frac{2 x+3}{(x+1)(x-3)}\)
సాధన.
\(\frac{2 x+3}{(x+1)(x-3)}=\frac{A}{x+1}+\frac{B}{x-3}\) అనుకుందాం.
∴ 2x + 3 = A(x – 3) + B(x + 1) …..(1)
(1) లో x = -1 వ్రాస్తే, 1 = A(-4) ⇒ A = \(-\frac{1}{4}\)
(1) లో x = 3 వ్రాస్తే, 9 = B(4) ⇒ B = \(\frac{9}{4}\)
\(\frac{2 x+3}{(x+1)(x-3)}=\frac{-1}{4(x+1)}+\frac{9}{4(x-3)}\)

ప్రశ్న 2.
\(\frac{5 x+6}{(2+x)(1-x)}\)
సాధన:
\(\frac{5 x+6}{(2+x)(1-x)}=\frac{A}{2+x}+\frac{B}{1-x}\) అనుకుందాం.
5x + 6 = A(1 – x) + B(2 + x) …..(1)
(1) లో x = -2 వ్రాస్తే, -10 + 6 = A(1 + 2) ⇒ A = \(-\frac{4}{3}\)
(1) లో x = 1 వ్రాస్తే, 5 + 6 = B(2 + 1) ⇒ B = \(\frac{11}{3}\)
∴ \(\frac{5 x+6}{(2+x)(1-x)}=-\frac{4}{3(2+x)}+\frac{11}{3(1-x)}\)

II.

ప్రశ్న 1.
\(\frac{3 x+7}{x^2-3 x+2}\)
సాధన:
\(\frac{3 x+7}{x^2-3 x+2}=\frac{3 x+7}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}\) అనుకుందాం.
3x + 7 = A(x – 2) + B(x – 1) ……(1)
(1) లో x = 1 వ్రాస్తే, 10 = -A ⇒ A = -10
(1) లో x = 2 వ్రాస్తే, 13 = B
∴ \(\frac{3 x+7}{x^2-3 x+2}=\frac{-10}{x-1}+\frac{13}{x-2}\)

ప్రశ్న 2.
\(\frac{x+4}{\left(x^2-4\right)(x+1)}\) [Mar. ’14]
సాధన:
\(\frac{x+4}{\left(x^2-4\right)(x+1)}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{x-2}\)
x + 4 = A(x2 – 4) + B(x + 1)(x – 2) + C(x + 1)(x + 2) …….(1)
(1) లో x = -1 వ్రాస్తే, 3 = A(1 – 4)
⇒ 3 = -3A
⇒ A = -1
(1) లో x = -2 వ్రాస్తే,
2 = B(-2 + 1) (-2 – 2)
⇒ 2 = 4B
⇒ B = \(\frac{1}{2}\)
(1) లో x = 2 వ్రాస్తే,
6 = C(2 + 1) (2 + 2)
⇒ 6 = 12C
⇒ C = \(\frac{1}{2}\)
∴ \(\frac{x+4}{\left(x^2-4\right)(x+1)}=-\frac{1}{x+1}+\frac{1}{2(x+2)}+\frac{1}{2(x-2)}\)

ప్రశ్న 3.
\(\frac{2 x^2+2 x+1}{x^3+x^2}\)
సాధన:
\(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{2 x^2+2 x+1}{x^2(x+1)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+1}\)
2x² + 2x + 1 = Ax(x + 1) + B(x + 1) + Cx² ……(1)
(1) లో x = 0 వ్రాస్తే, 1 = B
(1) లో x = -1 వ్రాస్తే, 2 – 2 + 1 = C(1) ⇒ C = 1
ఇరువైపులా x² గుణకాలు పోల్చగా
2 = A + C
⇒ A = 2 – C
= 2 – 1
= 1
∴ \(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\)

ప్రశ్న 4.
\(\frac{2 x+3}{(x-1)^3}\)
సాధన:
\(\frac{2 x+3}{(x-1)^3}\)
x – 1 = y అనుకుంటే x = y + 1
⇒ \(\frac{2 x+3}{(x-1)^3}=\frac{2(y+1)+3}{y^3}=\frac{2 y+5}{y^3}\)

ప్రశ్న 5.
\(\frac{x^2-2 x-6}{(x-2)^3}\)
సాధన:
x – 2 = y అనుకొనుము
⇒ x = y + 2

III.

ప్రశ్న 1.
\(\frac{x^2-x+1}{(x+1)(x-1)^2}\)
సాధన:
\(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{A}{x+1}+\frac{B}{x-1}+\frac{C}{(x-1)^2}\) అనుకుందాం.
x² – x + 1 = A(x – 1)² + B(x + 1)(x – 1) + C(x + 1) …….(1)
x = -1 వ్రాస్తే, 1 + 1 + 1 = A(4) ⇒ A = \(\frac{3}{4}\)
x = 1 వ్రాస్తే, 1 – 1 + 1 = C(2) ⇒ C = +\(\frac{1}{2}\)
1 లో x² గుణకాలను పోల్చగా
A + B = 1
⇒ B = 1 – A
⇒ B = 1 – \(\frac{3}{4}\)
⇒ B = \(\frac{1}{4}\)
∴ \(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{3}{4(x+1)}+\frac{1}{4(x-1)}+\frac{1}{2(x-1)^2}\)

ప్రశ్న 2.
\(\frac{9}{(x-1)(x+2)^2}\)
సాధన:
\(\frac{9}{(x-1)(x+2)^2}=\frac{A}{x-1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}\) అనుకొందాం.
9 = A(x + 2)² + B(x – 1) (x + 2) + C(x – 1) ……(1)
x = 1 వ్రాస్తే, 9 = 9A ⇒ A = 1
x = -2 వ్రాస్తే, 9 = -3C ⇒ C = -3
(1) లో x² గుణకాలను పోల్చగా
A + B = 0
⇒ B = -A = -1
∴ \(\frac{9}{(x-1)(x+2)^2}=\frac{1}{x-1}-\frac{1}{x+2}-\frac{3}{(x+2)^2}\)

ప్రశ్న 3.
\(\frac{1}{(1-2 x)^2(1-3 x)}\)
సాధన:
\(\frac{1}{(1-2 x)^2(1-3 x)}=\frac{A}{1-3 x}+\frac{B}{1-2 x}+\frac{C}{(1-2 x)^2}\) అనుకుందాం.
1 = A(1 – 2x)² + B(1 – 3x) (1 – 2x) + C(1 – 3x) ……..(1)
x = \(\frac{1}{3}\) వ్రాస్తే, 1 = A\(\left(1-\frac{2}{3}\right)^2\)
⇒ 1 = \(\frac{A}{9}\)
⇒ A = 9
x = \(\frac{1}{2}\) వ్రాస్తే, 1 = C(1 – \(\frac{3}{2}\))
⇒ 1 = \(-\frac{C}{2}\)
⇒ C = -2
(1) లో x² గుణకాలను పోల్చగా
0 = 4A + 6B
6B = -4A – 36
B = -6
∴ \(\frac{1}{(1-2 x)^2(1-3 x)}=\frac{9}{1-3 x}-\frac{6}{1-2 x}-\frac{2}{(1-2 x)^2}\)

ప్రశ్న 4.
\(\frac{1}{x^3(x+a)}\)
సాధన:
\(\frac{1}{x^3(x+a)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x^3}+\frac{D}{x+a}\) అనుకుందాం.
= \(\frac{A \cdot x^2(x+a)+B(x)(x+a)+C(x+a)+D x^3}{x^3(x+a)}\)
∴ 1 = A(x²) (x + a) + Bx(x + a) + C(x + a) + Dx³ ……..(1)
x = 0 ను (1) లో వ్రాస్తే, 1 = A(0) + B(0) + C(0 + a) + D(0)
⇒ 1 = C (a)
⇒ C = \(\frac{1}{a}\)
x = -a ను (1) లో వ్రాస్తే, 1 = A(0) + B(0) + C(0) + D(-a)³
⇒ 1 = D(-a³)
⇒ D = \(-\frac{1}{a^3}\)
(1) లో x³ గుణకాలను పోల్చగా
0 = A + D
⇒ A = -D
⇒ A = \(\frac{1}{a^3}\)
(1) లో x² గుణకాలను పోల్చగా
0 = Aa + B
⇒ B = -aA
⇒ B = \(-a\left(\frac{1}{a^3}\right)\)
⇒ B = \(-\frac{1}{a^2}\)

ప్రశ్న 5.
\(\frac{x^2+5 x+7}{(x-3)^3}\)
సాధన:

ప్రశ్న 6.
\(\frac{3 x^3-8 x^2+10}{(x-1)^4}\)
సాధన:

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(c) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(c)

అభ్యాసం – 6(సి)

ప్రశ్న 1.
క్రింది సమాసాల విలువలను 4 దశాంశాలకు సవరించి కనుక్కోండి.
(i) \(\sqrt[5]{242}\)
సాధన:

(ii) \(\sqrt[7]{127}\)
సాధన:

(iii) \(\sqrt[5]{32.16}\)
సాధన:

(iv) √199
సాధన:

(v) \(\sqrt[3]{1002}-\sqrt[3]{998}\)
సాధన:

(vi) \((1.02)^{3 / 2}-(0.98)^{3 / 2}\)
సాధన:

= 2[0.0299995]
= 0.0599990
≈ 0.059999
∴ \((1.02)^{3 / 2}-(0.98)^{3 / 2}\) = 0.059999

ప్రశ్న 2.
x² ఆపై x ఘాతాలు ఉపేక్షించేంతగా |x| స్వల్పమైతే క్రింది సమాసాల ఉజ్జాయింపు విలువలను కనుక్కోండి.
(i) \(\frac{(4+3 x)^{1 / 2}}{(3-2 x)^2}\)
సాధన:

(ii) \(\frac{\left(1-\frac{2 x}{3}\right)^{3 / 2}(32+5 x)^{1 / 5}}{(3-x)^3}\)
సాధన:

(iii) \(\sqrt{4-x}\left(3-\frac{x}{2}\right)^{-1}\)
సాధన:

(iv) \(\frac{\sqrt{4+x}+\sqrt[3]{8+x}}{(1+2 x)+(1-2 x)^{-1 / 3}}\)
సాధన:

(v) \(\frac{(8+3 x)^{2 / 3}}{(2+3 x) \sqrt{4-5 x}}\)
సాధన:

ప్రశ్న 3.
s, t లు ధన వాస్తవసంఖ్యలు, s తో పోల్చినపుడు t విలువ చాలా తక్కువ అయితే \(\left(\frac{s}{s+t}\right)^{1 / 3}-\left(\frac{s}{s-t}\right)^{1 / 3}\) యొక్క ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:
s తో పోల్చినపుడు విలువ చాలా తక్కువ కనుక \(\frac{t}{s}\) అత్యల్పం
∴ |\(\frac{t}{s}\)| < 1

ప్రశ్న 4.
p, q లు ధన వాస్తవ సంఖ్యలు, q తో సరి పోలిస్తే p విలువ చాలా తక్కువ అయితే \(\left(\frac{q}{q+p}\right)^{1 / 2}+\left(\frac{q}{q-p}\right)^{1 / 2}\) యొక్క ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:
q తో సరిపోలిస్తే p విలువ చాలా తక్కువ కనుక \(\frac{p}{q}\) అత్యల్పం

ప్రశ్న 5.
x⁴, ఆపై x ఘాతాలు ఉపేక్షిస్తే \(\sqrt[3]{x^2+64}-\sqrt[3]{x^2+27}\) యొక్క ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 6.
3√3 విలువను \(\frac{2}{3}\) యొక్క ఆరోహణ ఘాతాలలో వ్రాయండి.
సాధన:

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(b)

అభ్యాసం – 6(బి)

I.

ప్రశ్న 1.
క్రింది సమాసాలకు ద్విపద విస్తరణ వ్యవస్థితంచే x ల సమితులు కనుక్కోండి. [T.S. Mar. ’16, Mar. ’11]
(i) \((2+3 x)^{-2 / 3}\)
సాధన:

(ii) \((5+x)^{3 / 2}\)
సాధన:

(iii) (7 + 3x)^-5
సాధన:

(iv) \(\left(4-\frac{x}{3}\right)^{-1 / 2}\)
సాధన:

ప్రశ్న 2.
క్రింది విస్తరణలో సూచించిన పదాలు కనుక్కోండి.
(i) \(\left(1+\frac{x}{2}\right)^{-5}\) లో 6వ పదం
సాధన:

(ii) \(\left(1-\frac{x^2}{3}\right)^{-4}\) విస్తరణలో 7వ పదం
సాధన:

(iii) \((3-4 x)^{-2 / 3}\) విస్తరణలో 10వ పదం
సాధన:

(iv) \(\left(7+\frac{8 y}{3}\right)^{7 / 4}\) విస్తరణలో 5వ పదం
సాధన:

ప్రశ్న 3.
క్రింది విస్తరణలలో మొదటి 3 పదాలు వ్రాయండి.
(i) \((3+5 x)^{-7 / 3}\)
సాధన:

(ii) (1 + 4x)^-4
సాధన:

(iii) \((8-5 x)^{2 / 3}\)
సాధన:

(iv) \((2-7 x)^{-3 / 4}\)
సాధన:

ప్రశ్న 4.
క్రింది విస్తరణలో సాధారణ పదం ((r + 1)వ పదం) కనుక్కోండి.
(i) \((4+5 x)^{-3 / 2}\)
సాధన:

(ii) \(\left(1-\frac{5 x}{3}\right)^{-3}\)
సాధన:

(iii) \(\left(1+\frac{4 x}{5}\right)^{5 / 2}\)
సాధన:

(iv) \(\left(3-\frac{5 x}{4}\right)^{-1 / 2}\)
సాధన:

II.

ప్రశ్న 1.
\(\frac{1+2 x}{(1-2 x)^2}\) విస్తరణలో x10 గుణకం కనుక్కోండి.
సాధన:
\(\frac{1+2 x}{(1-2 x)^2}\) = (1 + 2x) (1 – 2x)^-2
= (1 + 2x) [1 + 2(2x) + 3(2x)² + 4(2x)³ + 5(2x)⁴ + 6(2x)⁵ + 7(2x)⁶ + 8(2x)⁷ + 9(2x)⁸ + 10(2x)⁹ + 11(2x)¹⁰ + …….. + (r + 1) . (2x)^r +……]
∴ \(\frac{1+2 x}{(1-2 x)^2}\) లో x¹⁰ గుణకం = (11) (2)¹⁰ + 10 (2) (2⁹)
= 2¹⁰ (11 + 10)
= 21 × 2¹⁰

ప్రశ్న 2.
\((1-4 x)^{-3 / 5}\) విస్తరణలో x⁴ గుణకం కనుక్కోండి.
సాధన:

ప్రశ్న 3.
(i) \(\frac{(1-3 x)^2}{(3-x)^{3 / 2}}\) విస్తరణలో x⁵ గుణకాన్ని కనుక్కోండి.
సాధన:

(ii) \(\frac{(1+x)^2}{\left(1-\frac{2}{3} x\right)^3}\) విస్తరణలో x⁸ గుణకాన్ని కనుక్కోండి.
సాధన:

(iii) \(\frac{(2+3 x)^3}{(1-3 x)^4}\) విస్తరణలో x⁷ గుణకాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 4.
\(\frac{\left(1+3 x^2\right)^{3 / 2}}{(3+4 x)^{1 / 3}}\) విస్తరణలో x³ గుణకాన్ని కనుక్కోండి.
సాధన:

III.

ప్రశ్న 1.
క్రింది అనంతశ్రేణుల మొత్తాలు కనుక్కోండి.
(i) \(1+\frac{1}{3}+\frac{1.3}{3.6}+\frac{1.3 .5}{3.6 .9}+\ldots \ldots \ldots\)
సాధన:
దత్తశ్రేణి S = \(1+\frac{1}{1} \cdot \frac{1}{3}+\frac{1.3}{1.2}\left(\frac{1}{3}\right)^2+\frac{1.3 \cdot 5}{1.2 .3}\left(\frac{1}{3}\right)^3\) + ……..

(ii) \(1-\frac{4}{5}+\frac{4.7}{5.10}-\frac{4.7 .10}{5.10 .15}+\ldots \ldots\)
సాధన:

(iii) \(\frac{3}{4}+\frac{3.5}{4.8}+\frac{3.5 .7}{4.8 .12}+\ldots\) (Mar. ’11)
సాధన:

(iv) \(\frac{3}{4.8}-\frac{3.5}{4.8 .12}+\frac{3.5 .7}{4.8 .12 .16}-\ldots \ldots\) [T.S. Mar. ’16]
సాధన:

ప్రశ్న 2.
t = \(\frac{4}{5}+\frac{4.6}{5.10}+\frac{4.6 .8}{5.10 .15}+\) …….∞ అయితే, 9t = 16 అని చూపండి.
సాధన:

ప్రశ్న 3.
x = \(\frac{1.3}{3.6}+\frac{1.3 .5}{3.6 .9}+\frac{1.3 .5 .7}{3.6 .9 .12}+\ldots \ldots\) అయితే 9x² + 24x = 11 అని చూపండి. [T.S. Mar. ’16]
సాధన:


3x = 3√3 – 4
⇒ 3x + 4 = 3√3
ఇరువైపుల వర్గం చేయగా
(3x + 4)² = (3√3)²
⇒ 9x² + 24x + 16 = 27
⇒ 9x² + 24x = 11

ప్రశ్న 4.
x = \(\frac{5}{(2 !) \cdot 3}+\frac{5.7}{(3 !) \cdot 3^2}+\frac{5 \cdot 7 \cdot 9}{(4 !) \cdot 3^3}+\ldots\) అయితే x² + 4x విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 5.
క్రింది అనంత శ్రేణి మొత్తం కనుక్కోండి. [A.P. Mar. ’16, Mar. ’05]
\(\frac{7}{5}\left(1+\frac{1}{10^2}+\frac{1.3}{1.2} \cdot \frac{1}{10^4}+\frac{1.3 .5}{1.2 .3} \cdot \frac{1}{10^6}+\ldots\right)\)
సాధన:

ప్రశ్న 6.
x ఒక శూన్యేతర అకరణీయ సంఖ్య అయితే \(1+\frac{x}{2}+\frac{x(x-1)}{2.4}+\frac{x(x-1)(x-2)}{2.4 .6}+\ldots \ldots\) \(=1+\frac{x}{3}+\frac{x(x+1)}{3.6}+\frac{x(x+1)(x+2)}{3.6 .9}+\ldots\) అని నిరూపించండి.
సాధన:

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(a)

అభ్యాసం – 6(ఎ)

I.

ప్రశ్న 1.
ద్విపద సిద్ధాంతాన్ని ఉపయోగించి క్రింది సమాసాలను విస్తరించి వ్రాయండి.
(i) (4x + 5y)⁷
సాధన:

(ii) \(\left(\frac{2}{3} x+\frac{7}{4} y\right)^5\)
సాధన:

(iii) \(\left(\frac{2 p}{5}-\frac{3 q}{7}\right)^6\)
సాధన:

(iv) (3 + x – x²)⁴
సాధన:

ప్రశ్న 2.
క్రింది పదాలు వ్రాసి సూక్ష్మీకరించండి.
(i) \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\) లో 6వ పదం [May ’13]
సాధన:

(ii) (3x – 4y)¹⁰ లో 7వ పదం
సాధన:

(iii) \(\left(\frac{3 p}{4}-5 q\right)^{14}\) లో 10వ పదం
సాధన:

(iv) \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\) లో rవ పదం (1 ≤ r ≤ 9)
సాధన:

ప్రశ్న 3.
క్రింది సమాసాల ద్విపద విస్తరణలలో పదాల సంఖ్యను కనుక్కోండి.
(i) \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\)
సాధన:
(x + a)ⁿ విస్తరణలో n పదాల సంఖ్య = (n + 1)
∴ \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\) ద్విపద విస్తరణలో పదాల సంఖ్య = 9 + 1 = 10

(ii) (3p + 4q)¹⁴
సాధన:
(3p + 4q)¹⁴ ద్విపద విస్తరణలో పదాల సంఖ్య = 14 + 1 = 15

(iii) (2x + 3y + z)⁷ [Mar. ’07; Mar. ’14, ’13]
సాధన:
(a + b + c)ⁿ విస్తరణలో పదాల సంఖ్య = \(\frac{(n+1)(n+2)}{2}\)
n ధన పూర్ణాంకం కనుక
(2x + 3y + z)⁷ లో పదాల సంఖ్య = \(\frac{(7+1)(7+2)}{2}\)
= \(\frac{8 \times 9}{2}\)
= 36

ప్రశ్న 4.
(4x – 7y)⁴⁹ + (4x + 7y)⁴⁹ విస్తరణలో శూన్యేతర గుణకాలు కలిగిన పదాలు ఎన్ని?
సాధన:

ప్రశ్న 5.
(1 + x)³⁹ విస్తరణలో చివరి 20 గుణకాల మొత్తం కనుక్కోండి.
సాధన:

ప్రశ్న 6.
(1 + x)²ⁿ, (1 + x)^2n-1 విస్తరణలలో A, B లు వరుసగా xn గుణకాలు అయితే \(\frac{A}{B}\) విలువ కనుక్కోండి.
సాధన:
ఇచ్చిన దత్తాంశం ప్రకారం (1 + x)²ⁿ మరియు (1 + x)^2n-1 విస్తరణలో xⁿ గుణకాలు A మరియు B అనుకొందాం.
∴ A = ²ⁿC_n
B = ^2n-1C_n

II.

ప్రశ్న 1.
క్రింది గుణకాలను కనుక్కోండి.
(i) \(\left(3 x-\frac{4}{x}\right)^{10}\) లో x^-6 గుణకం
సాధన:

(ii) \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\) లో x¹¹ గుణకం
సాధన:

(iii) \(\left(7 x^3-\frac{2}{x^2}\right)^9\) లో x² గుణకం
సాధన:

(iv) \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)^7\) లో x^-7 గుణకం
సాధన:

ప్రశ్న 2.
క్రింది సమాసాల ద్విపద విస్తరణలలో x లేని పదం (స్థిర పదం) కనుక్కోండి.
(i) \(\left(\frac{\sqrt{x}}{3}-\frac{4}{x^2}\right)^{10}\)
సాధన:

(ii) \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\)
సాధన:

(iii) \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\)
సాధన:

(iv) \(\left(\frac{2 x^2}{5}+\frac{15}{4 x}\right)^9\)
సాధన:

ప్రశ్న 3.
క్రింది సమాసాల ద్విపద విస్తరణలలో మధ్యపదం (పదాలు) కనుక్కోండి.
(i) \(\left(\frac{3 x}{7}-2 y\right)^{10}\)
సాధన:
(x + a)ⁿ విస్తరణలో n సరిసంఖ్య అయిన మధ్యపదం \(T_{\left(\frac{n+1}{2}\right)}\), n బేసిసంఖ్య అయిన రెండు పదాలు \(\frac{T_{n+1}}{2}\), \(\frac{T_{n+3}}{2}\) మధ్యపదాలు అవుతాయి.

(ii) \(\left(4 a+\frac{3}{2} b\right)^{11}\)
సాధన:

(iii) (4x² + 5x³)¹⁷
సాధన:

(iv) \(\left(\frac{3}{a^3}+5 a^4\right)^{20}\)
సాధన:

ప్రశ్న 4.
క్రింది సమాసాల ద్విపద విస్తరణలలో సంఖ్యాపరంగా గరిష్ఠ పదం (పదాలు) కనుక్కోండి.
(i) (4 + 3x)¹⁵, x = \(\frac{7}{2}\)
సాధన:

(ii) (3x + 5y)¹², x = \(\frac{1}{2}\), y = \(\frac{4}{3}\)
సాధన:

(iii) (4a – 6b)¹³, a = 3, b = 5
సాధన:

(iv) (3 + 7x)ⁿ, x = \(\frac{4}{5}\), n = 15
సాధన:
(3 + 7x)ⁿ = \(\left[3\left(1+\frac{7}{3} x\right)\right]^n\)

ప్రశ్న 5.
క్రింది వాటిని నిరూపించండి.
(i) 2.C₀ + 5.C₁ + 8.C₂ + ….. + (3n+2).C_n = (3n + 4) . 2^n-1
సాధన:

(ii) n ఒక సరిధన పూర్ణంకమైతే C₀ – 4 . C₁ + 7 . C₂ – 10 . C₃ + …… = 0
సాధన:

(iii) \(\frac{C_1}{2}+\frac{C_3}{4}+\frac{C_5}{6}+\frac{C_7}{8}+\ldots \ldots=\frac{2^n-1}{n+1}\)
సాధన:

(iv) \(C_0+\frac{3}{2} \cdot C_1+\frac{9}{3} \cdot C_2+\frac{27}{4} \cdot C_3+\ldots \ldots\) \(+\frac{3^n}{n+1} \cdot C_n=\frac{4^{n+1}-1}{3(n+1)}\)
సాధన:

(v) C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ….. + 2ⁿ . C_n = 3ⁿ [May ’07]
సాధన:

ప్రశ్న 6.
క్రింది మొత్తాలను కనుక్కోండి.
(i) \(\frac{{ }^{15} C_1}{{ }^{15} C_0}+2 \cdot \frac{{ }^{15} C_2}{{ }^{15} C_1}+3 \cdot \frac{{ }^{15} C_3}{{ }^{15} C_2}+\ldots \ldots\) \(+15 \cdot \frac{{ }^{15} C_{15}}{{ }^{15} C_{14}}\)
సాధన:

(ii) C₀ . C₃ + C₁ . C₄ + C₂ . C₅ + ….. + C_n-3 . C_n
సాధన:

(iii) 2² . C₀ + 3² . C₁ + 4² . C₂ + …… + (n+2)² . C_n
సాధన:

(iv) 3C₀ + 6C₁ + 12C₂ + …… + 3 . 2ⁿ . C_n
సాధన:

ప్రశ్న 7.
ద్విపద సిద్ధాంతాన్ని ఉపయోగించి ప్రతి ధన పూర్ణాంకం nకు 50ⁿ – 49n – 1 ను 49² భాగిస్తుందని చూపండి.
సాధన:

ప్రశ్న 8.
ద్విపద సిద్ధాంతాన్ని ఉపయోగించి ప్రతి ధన పూర్ణాంకం nకు 5⁴ⁿ + 52n – 1 ను 676 భాగిస్తుందని చూపండి.
సాధన:

ప్రశ్న 9.
(1 + x + x²)ⁿ = a₀ + a₁x + a₂x² + …… + a_2n x²ⁿ, అయితే
(i) a₀ + a₁ + a₂ + ……. + a_2n = 3ⁿ
(ii) a₀ + a₂ + a₄ + …… + a_2n = \(\frac{3^n+1}{2}\)
(iii) a₁ + a₃ + a₅ + …….. + a_2n-1 = \(\frac{3^n-1}{2}\)
(iv) a₀ + a₃ + a₆ + a₉ + …… = 3^n-1 అని చూపండి.
సాధన:

ప్రశ్న 10.
(1 + x + x² + x³)⁷ = b₀ + b₁x + b₂x² + ……. + b₂₁ x²¹ అయితే
(i) b₀ + b₂ + b₄ + …… + b₂₀
(ii) b₁ + b₃ + b₅ + ….. + b₂₁ విలువలు కనుక్కోండి.
సాధన:

ప్రశ్న 11.
\(\left(2+\frac{8 x}{3}\right)^n\) విస్తరణలో x¹¹, x¹² గుణకాలు సమానమైతే n విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 12.
2²⁰¹³ ను 17 తో భాగించగా వచ్చే శేషాన్ని కనుక్కోండి.
సాధన:
2⁴ = 16
2⁴ ను 17 తో భాగించగా వచ్చే శేషం – 1
2²⁰¹³ = (2⁴)⁵⁰³ . 2¹
∴ 2²⁰¹³ ను 17 తో భాగించగా వచ్చే శేషం (-1)⁵⁰³ . 2
= (-1) . 2
= -2

ప్రశ్న 13.
(1 + x)²¹ ద్విపద విస్తరణలో (2r + 4), (3r + 4) పదాల గుణకాలు సమానమయితే విలువ కనుక్కోండి.
సాధన:

III.

ప్రశ్న 1.
(1 + x)ⁿ విస్తరణలో x⁹, x¹⁰, x¹¹ పదాల గుణకాలు అంకశ్రేఢిలో ఉంటే, n² – 41n + 398 = 0 అని చూపండి.
సాధన:

ప్రశ్న 2.
(1 + x)ⁿ విస్తరణలో 3 వరస గుణకాలు 36, 84, 126 అయితే n విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 3.
(a + x)ⁿ విస్తరణలో 2, 3, 4 పదాల గుణకాలు వరుసగా 40, 70, 1080 అయితే a, x, n విలువలు కనుక్కోండి. [T.S. Mar ’16, May ’06]
సాధన:

ప్రశ్న 4.
(1 + x)ⁿ విస్తరణలో r, (r + 1), (r + 2) పదాల గుణకాలు అంకశ్రేఢిలో ఉంటే n² – (4r + 1)n + 4r² – 2 = 0 అని చూపండి.
సాధన:

ప్రశ్న 5.
\(\left(2 x^3-\frac{3}{x^2}\right)^{14}\) విస్తరణలో x³², x^-18 గుణకాల మొత్తం కనుక్కోండి.
సాధన:

ప్రశ్న 6.
(x + a)ⁿ ద్విపద విస్తరణలో బేసిపదాల మొత్తం P, సరిపదాల మొత్తం Q అయితే (i) P² – Q² = (x² – a²)ⁿ (ii) 4PQ = (x + a)²ⁿ – (x – a)²ⁿ అని నిరూపించండి. [A.P. Mar. ’16]
సాధన:

ప్రశ్న 7.
(1 + x)ⁿ ద్విపద విస్తరణలో 4 వరుస పదాల గుణకాలు వరుసగా a₁, a₂, a₃, a₄ అయితే \(\frac{a_1}{a_1+a_2}+\frac{a_3}{a_3+a_4}=\frac{2 a_2}{a_2+a_3}\) అని చూపండి. [Mar. ’11; May ’07]
సాధన:

ప్రశ్న 8.
\(\left({ }^{2 n} C_0\right)^2-\left({ }^{2 n} C_1\right)^2+\left({ }^{2 n} C_2\right)^2-\left({ }^{2 n} C_3\right)^2+\) ……. \(+\left({ }^{2 n} C_{2 n}\right)^2=(-1)^{22 n} C_n\) అని నిరూపించండి.
సాధన:

ప్రశ్న 9.
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) …. (C_n-1 + C_n) = \(\frac{(n+1)^n}{n !}\) · C₀ . C₁ . C₂ …… C_n అని నిరూపించండి.
సాధన:

ప్రశ్న 10.
\((1+3 x)^n\left(1+\frac{1}{3 x}\right)^n\) విస్తరణలో x లేని పదం (స్థిర పదం) కనుక్కోండి.
సాధన:

ప్రశ్న 11.
(1 + x)²ⁿ ద్విపద విస్తరణలోని మధ్యపదం \(\frac{1.3 .5 \ldots \ldots(2 n-1)}{n !}(2 x)^n\) అనిచూపండి. [May ’06]
సాధన:

ప్రశ్న 12.
(1 + 3x – 2x²)¹⁰ = a₀ + a₁x + a₂x² + …. + a₂₀x²⁰ అయితే
(i) a₀ + a₁ + a₂ + …… + a₂₀ = 2¹⁰
(ii) a₀ – a₁ + a₂ – a₃ + ……… + a₂₀ = 4¹⁰ అని నిరూపించండి.
సాధన:

ప్రశ్న 13.
(3√3 + 5)²ⁿ⁺¹ = x, f = x – [x] అయితే (ఇక్కడ [x] అనేది x పూర్ణాంక భాగాన్ని సూచిస్తుంది.), x . f విలువ కనుక్కోండి.
సాధన:
(3√3 + 5)²ⁿ⁺¹ = x
f = x – [x] ⇒ 0 < f < 1
F = (3√3 – 5)²ⁿ⁺¹ అనుకోండి.
5 < 3√3 < 6
⇒ 0 < 3√3 – 5 < 1
⇒ 0 < (3√3 – 5)²ⁿ⁺¹ < 1
⇒ 0 < F < 1
⇒ 0 > -F > -1
⇒ -1 < -F < 0

ప్రశ్న 14.
R, n లు ధన పూర్ణాంకాలు, n బేసి పూర్ణాంకం, 0 < F < 1, (5√5 + 11)ⁿ = R + F అయితే
(i) R ఒక సరి పూర్ణాంకం
(ii) (R + F) . F = 4ⁿ అని చూపండి.
సాధన:
(i) R, n లు ధన పూర్ణాంకాలు
0 < F < 1, (5√5 + 11)ⁿ = R + F
(5√5 – 11)ⁿ = f అనుకోండి.
121 < 125 < 144 కనుక
ఇప్పుడు 11 < 5√5 < 12
⇒ 0 < 5√5 – 11 < 1
⇒ 0 < (5√5 – 11)ⁿ < 1
⇒ 0 < f < 1
⇒ 0 > -f > -1
∴ -1 < -f < 0
R + F – f = (5√5 + 11)ⁿ – (5√5 – 11)ⁿ
= \(\left[{ }^n C_0(5 \sqrt{5})^n+{ }^n C_1(5 \sqrt{5})^{n-1}(11)\right.\)

ప్రశ్న 15.
I, n లు ధన పూర్ణాంకాలు 0 < f < 1, (7 + 4√3)ⁿ = I + f అయితే
(i) I ఒక బేసి పూర్ణాంకం
(ii) (I + f) (I – f) = 1 అని చూపండి.
సాధన:
I, n లు ధన పూర్ణాంకాలు
(7 + 4√3)ⁿ = I + f, 0 < f < 1
7 – 4√3 = F అనుకోండి.
∴ 36 < 48 < 49
ఇప్పుడు 6 < 4√3 < 7
⇒ -6 > 4√3 > -7
⇒ -7< -4√3 < -6
⇒ 0 < (7 – 4√3)ⁿ < 1
∴ 0 < F < 1
I + f + F = (7 + 4√3)ⁿ + (7 – 4√3)ⁿ

= \(2\left[{ }^n C_0 7^n+{ }^n C_2 7^{n-2}(4 \sqrt{3})^2+\ldots . .\right]\)
= 2k, k పూర్ణాంకం
∴ I + f + F సరిపూర్ణాంకం.
⇒ f + F పూర్ణాంకం, (I పూర్ణాంకం కనుక)
కానీ 0 < f < 1, 0 < F < 1
⇒ 0 < f + F < 2
∴ f + F = 1 …….(1)
⇒ I + 1 సరి పూర్ణాంకం.
∴ I బేసి పూర్ణాంకం.
(I + f) (I – f) = (I + f) F, (1) నుండి
= (7 + 4√3)ⁿ (7 – 4√3)ⁿ
= [(7 + 4√3) (7 – 4√3)]ⁿ
= (49 – 48)ⁿ
= 1

ప్రశ్న 16.
n ధన పూర్ణాంకం అయితే \(\sum_{r=1}^n r^3\left(\frac{{ }^n C_r}{{ }^n C_{r-1}}\right)^2=\frac{(n)(n+1)^2(n+2)}{12}\) అని నిరూపించండి.
సాధన:

ప్రశ్న 17.
\(\left(5^{1 / 6}+2^{1 / 8}\right)^{100}\) విస్తరణలో కరణీయ పదాల సంఖ్యను కనుకోండి.
సాధన:
సాధారణ పదం
\(T_{r+1}={ }^{100} C_r\left(5^{1 / 6}\right)^{100-r}\left(2^{1 / 8}\right)^r\) = \({ }^{100} C_r 5^{\frac{100-r}{6}} \cdot 2^{\frac{r}{8}}\)
0 ≤ r ≤ 100 లో r = 4, 10, 16, 22, 28, 34, 40, 46, 52, 58, 64, 70, 76, 82, 88, 94, 100 అయితే \(\frac{100-r}{6}\) ఒక పూర్ణాంకం
0 ≤ r ≤ 100 లో r = 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96\(\frac{r}{8}\) ఒక పూర్ణాంకం
0 ≤ r ≤ 100 అయితే r = 16, 40, 64, 88 అయితే \(\frac{100-r}{6}, \frac{r}{8}\) లు రెండూ పూర్ణాంకాలు
∴ \(\left(5^{1 / 6}+2^{1 / 8}\right)^r\) విస్తరణలో అకరణీయ పదాలు = 4
∴ \(\left(5^{1 / 6}+2^{1 / 8}\right)^r\) విస్తరణలో కరణీయ పదాల సంఖ్య = 101 – 4 = 97

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(e) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(e)

అభ్యాసం – 5(ఇ)

I.

ప్రశ్న 1.
ⁿC₄ = 210, అయితే n విలువ ఎంత?
సాధన:
సూచన: ⁿC_r = \(\frac{n !}{(n-r) ! r !}\) = \(\frac{n \cdot(n-1)(n-2) \ldots \ldots / n-(r-1)]}{1.2 .3 \ldots \ldots \ldots . .}\)
ⁿC₄ = 210
⇒ \(\frac{n(n-1)(n-2)(n-3)}{1.2 .3 .4}\) = 10 × 21
⇒ n(n – 1) (n – 2) (n – 3) = 10 × 21 × 1 × 2 × 3 × 4
⇒ n(n – 1) (n – 2) (n – 3) = 10 × 7 × 3 × 2 × 3 × 4
⇒ n(n – 1) (n – 2) (n – 3) = 10 × 9 × 8 × 7
∴ n = 10

ప్రశ్న 2.
¹²C_r = 495, అయితే r విలువ కనుక్కోండి.
సాధన:
సూచన: ⁿC_r = ⁿC_n-r
¹²C_r = 495
= 5 × 99
= 11 × 9 × 5
= \(\frac{12 \times 11 \times 9 \times 5 \times 2}{12 \times 2}\)
= \(\frac{12 \times 11 \times 10 \times 9}{1.2 .3 .4}\)
= ¹²C₄ లేదా ¹²C₈
∴ r = 4 లేదా 8

ప్రశ్న 3.
10 . ⁿC₂ = 3 . ⁿ⁺¹C₃, అయితే n విలువ ఎంత?
సాధన:
10 . ⁿC₂ = 3 . ⁿ⁺¹C₃
⇒ 10 × \(\frac{n(n-1)}{1.2}=\frac{3(n+1) n(n-1)}{1.2 .3}\)
⇒ 10 = n + 1
⇒ n = 9

ప్రశ్న 4.
ⁿP_r = 5040, ⁿC_r = 210 అయితే n, r విలువలను కనుక్కోండి. [A.P. Mar. ’16]
సాధన:
సూచన: ⁿP_r = r! ⁿC_r మరియు ⁿP_r = n(n – 1) (n – 2)…. [n – (r – 1)]
ⁿP_r = 5040, ⁿC_r = 210
r! = \(\frac{{ }^n P_r}{{ }^n C_r}=\frac{5040}{210}=\frac{504}{21}\) = 24 = 4!
∴ r = 4
ⁿP_r = 5040
ⁿP₄ = 5040
= 10 × 504
= 10 × 9 × 56
= 10 × 9 × 8 × 7
= ¹⁰P₄
∴ n = 10
∴ n = 10, r = 4

ప్రశ్న 5.
ⁿC₄ = ⁿC₆, అయితే n ఎంత?
సాధన:
సూచన: ⁿC_r = ⁿC_s ⇒ r = s or r + s = n
ⁿC₄ = ⁿC₆
∴ n = 4 + 6 = 10

ప్రశ్న 6.
¹⁵C_2r-1 = ¹⁵C_2r+4 అయితే r విలువ కనుక్కోండి. [Mar. ’14, ’05]
సాధన:
¹⁵C_2r-1 = ¹⁵C_2r+4
⇒ 2r – 1 = 2r + 4 లేదా (2r – 1) + (2r + 4) = 15
⇒ 4r + 3 = 15
⇒ 4r = 12
⇒ r = 3
∴ 2r – 1 = 2r + 4
⇒ -1 = 4 ఇది అసాధ్యం
∴ r = 3

ప్రశ్న 7.
¹⁷C_2t+1 = ¹⁷C_3t-5, అయితే t విలువ ఎంత?
సాధన:
¹⁷C_2t+1 = ¹⁷C_3t-5
⇒ 2t + 1 = 3t – 5 లేదా (2t + 1) + (3t – 5) = 17
⇒ 1 + 5 = t లేదా 5t = 21
⇒ t = 6 లేదా t = \(\frac{21}{5}\) ఇది పూర్ణాంకము కాదు
∴ t = 6

ప్రశ్న 8.
¹²C_r+1 = ¹²C_3r-5, అయితే r విలువ కనుక్కోండి. [T.S. Mar. ’16, Mar. ’08]
సాధన:
¹²C_r+1 = ¹²C_3r-5
⇒ r + 1 = 3r – 5 లేదా (r + 1) + (3r – 5) = 12
⇒ 1 + 5 = 2r లేదా 4r – 4 = 12
⇒ 2r = 6 లేదా 4r = 16
⇒ r = 3 లేదా r = 4
∴ r = 3 లేదా 4

ప్రశ్న 9.
⁹C₃ + ⁹C₅ = ¹⁰C_r, అయితే r విలువ కనుక్కోండి?
సాధన:
సూచన: ⁿC_r = ⁿC_n-r
¹⁰C_r = ⁹C₃ + ⁹C₅
∴ ⁿC_r + ⁿC_r-1 = ⁽ⁿ⁺¹⁾C_r
⁹C₆ + ⁹C₅ = ¹⁰C₆ లేదా ¹⁰C₄
∴ r = 4 లేదా 6

ప్రశ్న 10.
ఆరుగురు పురుషులు ముగ్గురు స్త్రీల నుంచి అయిదుగురు సభ్యులున్న కమిటీలు ఎన్ని ఏర్పరచవచ్చు?
సాధన:
వ్యక్తుల సంఖ్య = 6 + 3 = 9
ఈ 9 మంది నుండి 5 గురు సభ్యులున్న కమిటీ ఏర్పరచే విధానాలు = ⁹C₅
= ⁹C₄
= \(\frac{9 \times 8 \times 7 \times 6}{1 \times 2 \times 3 \times 4}\)
= 126

ప్రశ్న 11.
పై ప్రశ్నలో కనీసం ఇద్దరు స్త్రీలు ఉండే కమిటీలు ఎన్ని?
సాధన:
కమిటీలో కనీసం ఇద్దరు స్త్రీలు ఉండేటట్లుగా కమిటీలను ఈక్రింది విధంగా ఎన్నుకోవచ్చు.
(i) ముగ్గురు పురుషులు, ఇద్దరు స్త్రీలు
ముగ్గురు పురుషులు, ఇద్దరు స్త్రీలను ఎన్నుకొనే విధానాల సంఖ్య = ⁶C₃ × ³C₂
= 20 × 3
= 60
(ii) ఇద్దరు పురుషులు, ముగ్గురు స్త్రీలు
ఇద్దరు పురుషులు, ముగ్గురు స్త్రీలను ఎన్నుకొనే విధానాల సంఖ్య = ⁶C₂ × ³C₂
= 15 × 1
= 15
∴ కనీసం ఇద్దరు స్త్రీలు ఉండేటట్లుగా కమిటీలను ఎన్ను కొనే విధానాల సంఖ్య = 60 + 15 = 75

ప్రశ్న 12.
ⁿC₅ = ⁿC₆, అయితే ¹³C_n విలువ ఎంత? [Mar. ’13]
సాధన:
ⁿC₅ = ⁿC₆
⇒ n = 6 + 5 = 11
¹³C_n = ¹³C₁₁
= ¹³C₂
= \(\frac{13 \times 12}{1 \times 2}\)
= 78

II.

ప్రశ్న 1.
3 ≤ r ≤ n కు ^(n-3)C_r + 3 ^(n-3)C_r-1 + 3 ^(n-3)C_r-2 + ^(n-3)C_r-3 = ⁿC_r అని నిరూపించండి.
సాధన:

ప్రశ్న 2.
¹⁰C₅ + 2 . ¹⁰C₄ + ¹⁰C₃ విలువ ఎంత?
సాధన:
సూచన: ⁿC_r + ⁿC_r-1 = ⁽ⁿ⁺¹⁾C_r
¹⁰C₅ + 2 . ¹⁰C₄ + ¹⁰C₃

ప్రశ్న 3.
సూక్ష్మీకరించండి ³⁴C₅ + \(\sum_{r=0}^4(38-r) C_4\)
సాధన:

ప్రశ్న 4.
ఒక తరగతిలో 30 మంది విద్యార్థులున్నారు. వారిలో ప్రతి విద్యార్థి మిగిలిన విద్యార్థులందరితో ఒక చదరంగం ఆటను ఆడితే మొత్తం ఎన్ని చదరంగం ఆటలు వారు ఆడినట్లు?
సాధన:
తరగతిలోని విద్యార్థుల సంఖ్య = 30
ప్రతి విద్యార్థి మిగిలిన విద్యార్థులందరితో ఒక్కో చదరంగం ఆటను ఆడతాడు.
కనుక మొత్తం చదరంగం ఆటల సంఖ్య = ³⁰C₂
= \(\frac{30 \times 29}{1 \times 2}\)
= 435

ప్రశ్న 5.
ఏడుగురు బాలికలు, ఆరుగురు బాలురు నుంచి ముగ్గురు బాలురు, ముగ్గురు బాలికలు ఉండే కమిటీలను ఎన్ని రకాలుగా ఏర్పరచవచ్చు?
సాధన:
ఏడుగురు బాలికలు, ఆరుగురు బాలురు నుండి ముగ్గురు బాలురు, ముగ్గురు బాలికలు ఉండే కమిటీల సంఖ్య = ⁷C₃ × ⁶C₃
= 35 × 20
= 700

ప్రశ్న 6.
10 మంది వ్యక్తుల నుంచి నిర్దేశించిన ఒక వ్యక్తి ఉండేలా ఆరుగురు సభ్యుల కమిటీలు ఎన్ని ఏర్పరచవచ్చు?
సాధన:
నిర్దేశించిన వ్యక్తి కమిటీలో ఉండి, మిగిలిన 9 మంది నుండి 5 గురు వ్యక్తులను ఎన్నుకొనే విధాల సంఖ్య = ⁹C₅
∴ 10 మంది వ్యక్తుల నుంచి నిర్దేశించిన వ్యక్తి ఉండేలా ఆరుగురు సభ్యుల కమిటీలు ఎన్నుకొనే విధాల సంఖ్య = ⁹C₅
= \(\frac{9 \times 8 \times 7 \times 6 \times 5}{1 \times 2 \times 3 \times 4 \times 5}\)
= 126

ప్రశ్న 7.
ఇచ్చిన 9 పుస్తకాల నుంచి నిర్దేశించిన ఒక పుస్తకం లేకుండా 5 పుస్తకాలను ఎన్ని రకాలుగా ఎంచుకోవచ్చు?
సాధన:
9 పుస్తకాలనుంచి నిర్దేశించిన ఒక పుస్తకం లేకుండా 5 పుస్తకాలు ఎన్నుకోవాలి. అంటే నిర్దేశించిన ఆ పుస్తకం తీసివేసి, మిగిలిన 8 పుస్తకాల నుండి 5 పుస్తకాలు ఎంచుకోవాలి. ఈ పనిని 8C5 విధాలుగా చేయవచ్చు.
కనుక కావలసిన సంయోగాల సంఖ్య = ⁸C₅
= ⁸C₃
= \(\frac{8 \times 7 \times 6}{1 \times 2 \times 3}\)
= 56

ప్రశ్న 8.
EQUATION పదంలోని అక్షరాల నుంచి 3 అచ్చులు, 2 హల్లులు ఎన్ని రకాలుగా ఎంచుకోవచ్చు? [May ’11, Mar. ’07]
సాధన:
EQUATION అనే పదంలో {E, U, A, I, O} అను 5 అచ్చుల {Q, T, N} అను 3 హల్లులు కలవు.
అందులో 3 అచ్చులు, 2. హల్లులు ఎన్నుకొనే విధాలు = ⁵C₃ × ³C₂
= 10 × 3
= 30

ప్రశ్న 9.
12 భుజాలున్న ఒక బహుభుజి కర్ణాల సంఖ్య కనుక్కోండి.
సాధన:
ఇచ్చట n = 12
n భుజాలున్న బహుభుజి కర్ణాల సంఖ్య = \(\frac{n(n-3)}{2}\)
= \(\frac{12 \times 9}{2}\)
= 54

ప్రశ్న 10.
ఒక వరుసలో ఉన్న n వ్యక్తుల నుంచి పక్క పక్కనే ఉన్న ఇద్దరు వ్యక్తులను ఎన్ని రకాలుగా ఎంచుకోవచ్చు?
సాధన:
ఒక వరుసలో ఉన్న n వ్యక్తుల నుంచి, పక్కపక్కనే ఉన్న ఇద్దరు వ్యక్తులను ఎంచుకొనే విధాల సంఖ్య = n – 1

ప్రశ్న 11.
4 సరూప నాణేలను 5 గురు బాలురకు ఎవరికైనా ఎన్నైనా ఇచ్చే పద్ధతిలో ఎన్ని రకాలుగా పంచవచ్చు?
సాధన:
4 సరూప నాణేలను ఈ క్రింది విభిన్న సమూహాలుగా విభజించవచ్చు.
(i) ఒక సమూహంలో 4 నాణేలు
(ii) రెండు సమూహాలలో వరుసగా 1, 3 నాణేలు
(iii) రెండు సమూహాలలో వరుసగా 2, 2 నాణేలు
(iv) రెండు సమూహాలలో వరుసగా 3, 1 నాణేలు
(v) మూడు సమూహాలలో వరుసగా 1, 1, 2 నాణేలు
(vi) మూడు సమూహాలలో వరుసగా 1, 2, 1 నాణేలు
(vii) మూడు సమూహాలలో వరుసగా 2, 1, 1 నాణేలు
(viii) నాలుగు సమూహాలలో వరుసగా 1, 1, 1, 1 నాణేలు
ఈ సమూహాలను 5 గురు బాలురకు పంచే విధాల సంఖ్య
= \({ }^5 C_1+2 \times{ }^5 C_2+{ }^5 C_2+{ }^5 C_3 \times \frac{3 !}{2 !}+{ }^5 C_4\)
= 5 + 20 + 10 + 30 + 5
= 70

III.

ప్రశ్న 1.
\(\frac{{ }^{4 n} C_{2 n}}{{ }^{2 n} C_n}=\frac{1.3 .5 \ldots \ldots(4 n-1)}{\{1.3 .5 \ldots \ldots(2 n-1)\}^2}\) అని నిరూపించండి.
సాధన:

ప్రశ్న 2.
ఒక సమితి A లో 12 మూలకాలున్నాయి. ఆ సమితిలో
(i) 4 మూలకాలున్న ఉపసమితులెన్ని?
(ii) కనీసం 3 మూలకాలున్న ఉపసమితులెన్ని?
(iii) 3 లేదా అంతకంటే తక్కువ మూలకాలున్న ఉపసమితులెన్ని? [May ’07]
సాధన:
సమితి A లో వున్న మూలకాల సంఖ్య = 12
(i) 4 మూలకాలున్న ఉపసమితుల సంఖ్య = ¹²C₄
= \(\frac{2 \times 11 \times 10 \times 9}{1 \times 2 \times 3 \times 4}\)
= 495
(ii) కనీసం 3 మూలకాలున్న ఉపసమితులు.
పై లెక్క ప్రకారం కనీసం రెండు మూలకాలున్న ఉపసమితులు = ¹²C₀ + ¹²C₁ + ¹²C₂
= 1 + 12 + 66
= 79
A సమితికున్న మొత్తం ఉపసమితుల సంఖ్య = 2¹²
∴ కనీసం 3 మూలకాలున్న ఉపసమితులు = 2¹² – (79)
= 4096 – 79
= 4017
(iii) 3 లేదా అంతకంటే తక్కువ మూలకాలున్న ఉప సమితులు సున్నా మూలకాలు
(i.e.,) మూలకాలు లేని ఉపసమితిల సంఖ్య = ¹²C₀ = 1
ఒకే ఒక మూలకము వున్న ఉపసమితులు = ¹²C₁ = 12
రెండు మూలకములు వున్న ఉపసమితులు = ¹²C₂
= \(\frac{12 \times 11}{1 \times 2}\)
= 66
మూడు మూలకములు వున్న ఉపసమితులు = ¹²C₃
= \(\frac{12 \times 11 \times 10}{1 \times 2 \times 3}\)
= 220
∴ కనీసం 3 మూలకాలున్న ఉపసమితులు = 1 + 12 + 66 + 220 = 299

ప్రశ్న 3.
ఏడుగురు బాట్స్మెన్, ఆరుగురు బౌలర్లు నుంచి కనీసం అయిదుగురు బౌలర్లు ఉన్న పదకొండు మంది క్రికెట్ టీమును ఎన్ని రకాలుగా ఏర్పరచవచ్చు?
సాధన:
కనీసం 5 గురు బౌలర్లు ఉన్న పదకొండు మంది క్రికెట్ టీమును క్రింద చూపిన విధాలుగా ఎంచుకోవచ్చు.

∴ కోరిన విధంగా క్రికెట్ టీముని ఎంచుకొనే విధానాలు = 42 + 21 = 63

ప్రశ్న 4.
5 అచ్చులు, 6 హల్లులు నుంచి 3 అచ్చులు, 3 హల్లులు ఉండేలా ఎన్ని 6 అక్షరాల పదాలు ఏర్పరచవచ్చు.
సాధన:
అచ్చుల సంఖ్య = 5
హల్లుల సంఖ్య = 6
5 అచ్చుల నుండి 3 అచ్చులు ఎన్నుకొనే విధానాల సంఖ్య = ⁵P₃
6 హల్లులు నుండి 3 హల్లులు ఎన్నుకొనే విధానాల సంఖ్య = ⁶P₃
ఈ 6 అక్షరాలను వాటిలో వాటిని మార్చి వ్రాయగల పదాల సంఖ్య 6!
∴ 6 అక్షరాల పదాలలో 3 అచ్చులు 3 హల్లులు ఉండేలా ఎన్నుకోగల పదాల సంఖ్య = ⁵C₃ × ⁶C₃ × 6!

ప్రశ్న 5.
ఒక రైలు మార్గంలో 8 స్టేషన్లు ఉన్నాయి. వీటిలో 3 స్టేషన్లలో రైలు ఆపాలి. ఆ మూడు స్టేషన్లలో ఏ రెండూ పక్కపక్కన లేకుండా ఎన్ని రకాలుగా ఎంచుకోవచ్చు? [Mar. ’08]
సాధన:
మొదటి రైలు ఆగే స్టేషన్ ముందు గల స్టేషన్ల సంఖ్య x₁ అనుకోండి. ఇట్లే మొదట, రెండు రైలు ఆగే మధ్య x₂ స్టేషన్లు, రెండు, మూడు రైలు ఆగే స్టేషన్ల మధ్య x₃, స్టేషన్లు మరియు మూడవసారి రైలు ఆగిన తరువాత x₄ స్టేషన్లు ఉన్నాయి అనుకోండి.
అప్పుడు x₁ ≥ 0, x₂ ≥ 1, x₃ ≥ 1, x₄ ≥ 0 మరియు x₁ + x₂ + x₃ + x₄ = n – 3
ఈ సమీకరణానికి గల సాధనల సంఖ్య ⁶C₃
∴ ఏ రెండు స్టేషన్లు పక్క పక్కన లేకుండా 8 స్టేషన్లలో 3 స్టేషన్లు ఎంచుకొనే విధానాలు = ⁶C₃
= \(\frac{6 \times 5 \times 4}{1 \times 2 \times 3}\)
= 20

ప్రశ్న 6.
ఆరుగురు భారతీయులు, అయిదుగురు అమెరికా దేశస్థుల నుంచి అయిదుగురు సభ్యులున్న కమిటీని, ఆ కమిటీలో భారతీయుల సంఖ్య పెద్దదిగా ఉండేలా ఎన్ని రకాలుగా ఎంచుకోవచ్చు? [Mar. ’13, ’08]
సాధన:
కమిటీలో భారతీయుల సంఖ్య పెద్దదిగా ఉండేటట్లు కమిటీని ఎన్నుకొనే విధాలు ఈ క్రింద ఇవ్వబడినవి.

∴ కమిటీని కోరిన విధంగా ఎంచుకొనే విధానాల సంఖ్య = 200 + 75 + 6 = 281

ప్రశ్న 7.
ఒక ప్రశ్నాపత్రంలో A, B, C అనే మూడు భాగాలలో వరుసగా 3, 4, 5 ప్రశ్నలున్నాయి. ఒక్కో భాగం నుంచి కనీసం ఒక ప్రశ్న ఉండే విధంగా మొత్తం 6 ప్రశ్నలు ఎన్ని రకాలుగా ఎంచుకోవచ్చు?
సాధన:
మొదటి పద్దతి
ఒక్కొక్క భాగం నుంచి ఒక ప్రశ్న ఉండే విధంగా 6 ప్రశ్నలు ఎన్నుకొనే విధాలు ఈ క్రింది ఇవ్వబడినవి.

రెండవ పద్ధతి
ఒక్కో భాగం నుంచి కనీసం ఒక ప్రశ్న ఉండే విధంగా మొత్తం 6 ప్రశ్నలు ఎంచుకొనే విధాలు = మొత్తం 12 ప్రశ్నల నుండి 6 ప్రశ్నలు ఎంచుకొనే విధాలు – C భాగం నుండి కాక మిగిలిన రెండు భాగాల నుండి 6 ప్రశ్నలు ఎన్నుకోవడం – B నుండి కాక మిగిలిన రెండు భాగాల నుండి 6 ప్రశ్నలు ఎన్నుకోవటం – A నుండి కాక మిగిలిన రెండు భాగాల నుండి 6 ప్రశ్నలు ఎన్నుకోవడం
= ¹²C₆ – ⁷C₆ – ⁸C₆ – ⁹C₆
= 805

ప్రశ్న 8.
12 విభిన్నమైన వస్తువులను ఎన్నిరకాలుగా
(i) 4 సమభాగాలుగా చేయవచ్చు
(ii) నలుగురు వ్యక్తులకు సమానంగా పంచవచ్చు?
సాధన:
(i) 12 విభిన్న వస్తువులను 4 సమభాగాలుగా విభజించే విధానాలు = \(\frac{(12) !}{(3)^4 4 !}\)
(ii) నలుగురు వ్యక్తులకు సమానంగా 12 విభిన్న వస్తువులు పంచే విధాల సంఖ్య = \(\frac{(12) !}{(3 !)^4}\)

ప్రశ్న 9.
ఒక తరగతిలో నలుగురు బాలురు, ఆ బాలికలున్నారు. ప్రతీ ఆదివారం వారిలో కనీసం ముగ్గురు బాలురు ఉండేలా 5 గురు ఉన్న సమూహం విహారయాత్రకు వెళ్తారు. ప్రతీ ఆదివారం వేర్వేరు సమూహాలు విహారయాత్రకు వెళ్తాయి. వారి తరగతి ఉపాధ్యాయిని విహార యాత్రకు వచ్చిన ప్రతీ అమ్మాయికి ప్రతిసారి ఒక్కో బొమ్మ ఇవ్వగా వచ్చే మొత్తం బొమ్మల సంఖ్య 85 ఐతే g విలువ కనుక్కోండి.
సాధన:
బాలుర సంఖ్య = 4
బాలికల సంఖ్య = g
కనీసం ముగ్గురు బాలురు ఉండేలా ఈ క్రింది పట్టికలో తెలిపిన విధంగా ఎన్నుకొనవచ్చును.

G₁ లో బాలికల సంఖ్య = [⁴C₃ × ⁹C₂] × 2 ఎందువలననగా ప్రతిసారి ఇద్దరు బాలికలు ఉంటారు.
G₂ లో బాలికల సంఖ్య = [⁴C₃ × ⁹C2] × 1 ఎందువలననగా ప్రతిసారి ఒక బాలిక ఉంటుంది.
మొత్తం బాలికలకు ఇచ్చిన బొమ్మల సంఖ్య = 85
⇒ [⁴C₃ × ⁹C₂] × 2 + [⁴C₃ × ⁹C₂] × 1 = 85
⇒ 4 . \(\frac{g(g-1)}{2}\) × 2 + 1 . g . 1 = 85
⇒ 4g² – 4g + g – 85 = 0
⇒ 4g² – 3g – 85 = 0
⇒ 4g² – 20g + 17g – 85 = 0
⇒ 4g(g – 5) + 17(g – 5) = 0
⇒ (g – 5) (4g + 17) = 0
g ≠ \(\frac{17}{5}\) కనుక
∴ g = 5
∴ బాలికల సంఖ్య = 5