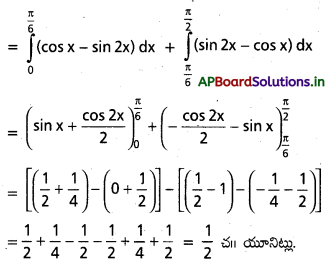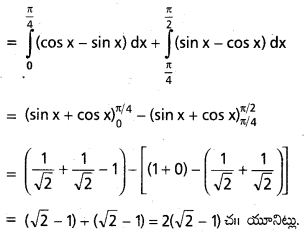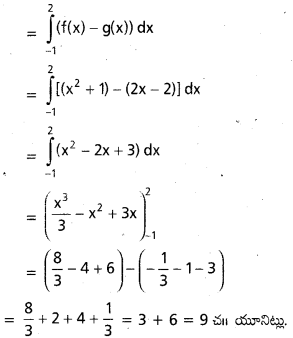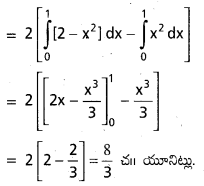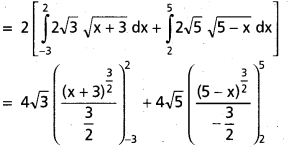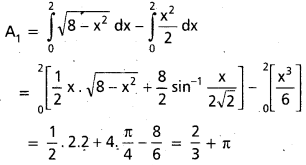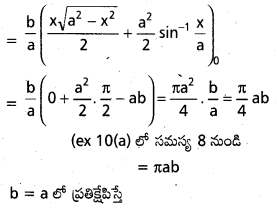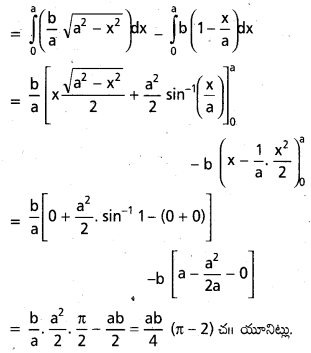Srinivas

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 6 సమాకలనం Exercise 6(d) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 6 సమాకలనం Exercise 6(d)

అభ్యాసం 6(డి)

I. కింది సమాకలనులను సాధించండి

ప్రశ్న 1.
∫\(\frac{1}{\sqrt{2 x-3 x^2+1}}\)dx
సాధన:

ప్రశ్న 2.
∫\(\frac{\sin \theta}{\sqrt{2-\cos ^2 \theta}}\) dθ
సాధన:

ప్రశ్న 3.
∫\(\frac{\cos x}{\sin ^2 x+4 \sin x+5}\) dx (Mar. 07)
సాధన:
t = sin x ⇒ dt = cos x dx
I = ∫\(\frac{d t}{t^2+4 t+5}\) = ∫\(\frac{d t}{(t+2)^2+1}\)
= tan^-1(t + 2) + C
= tan^-1(sin x + 2) + C

ప్రశ్న 4.
∫\(\frac{d x}{1+\cos ^2 x}\)
సాధన:

ప్రశ్న 5.
∫\(\frac{d x}{2 \sin ^2 x+3 \cos ^2 x}\)
సాధన:
∫\(\frac{d x}{2 \sin ^2 x+3 \cos ^2 x}\) = ∫\(\frac{\sec ^2 x d x}{2 \tan ^2 x+3}\)
t = tan x ⇒ dt = sec²x dx

ప్రశ్న 6.
∫\(\frac{1}{1+\tan x}\) dx
సాధన:

ప్రశ్న 7.
∫\(\frac{1}{1-\cot x}\) dx
సాధన:

II. కింది సమాకలనులను సాధించండి.

ప్రశ్న 1.
∫\(\sqrt{1+3 x-x^2}\) dx (May ’11)
సాధన:
∫\(\sqrt{1+3 x-x^2}\) = ∫\(\sqrt{1-\left(x^2-3 x\right)}\) dx

ప్రశ్న 2.
∫\(\frac{9 \cos x-\sin x}{4 \sin x+5 \cos x} d x\) (Mar. 08)
సాధన:

ప్రశ్న 3.
∫\(\frac{2 \cos x+3 \sin x}{4 \cos x+5 \sin x} d x\)
సాధన:
2 cos x + 3 sin x = A(4 cos x + 5 sin x) + B(-4 sin x + 5 cós x) అనుకొండి.
sin x, cos x గుణకాలను సమానం చేయండి
4A + 5B = 2
5A – 4B = 3

= \(\frac{23}{41}\)x – \(\frac{2}{41}\). log |4 cos x + 5 sin x| + C

ప్రశ్న 4.
∫\(\frac{1}{1+\sin x+\cos x}\)dx
సాధన:

ప్రశ్న 5.
∫\(\frac{1}{3 x^2+x+1}\)dx
సాధన:

ప్రశ్న 6.
∫\(\frac{d x}{\sqrt{5-2 x^2+4 x}}\)
సాధన:
5 – 2x² + 4x

III. కింది సమాకనులను గణించండి

ప్రశ్న 1.
∫\(\frac{x+1}{\sqrt{x^2-x+1}}\) dx
సాధన:

ప్రశ్న 2.
∫(6x + 5)\(\sqrt{6-2 x^2+x}\) dx (May 06)
సాధన:
6x + 5 = A(1 – 4x) + B అనుకొండి
x గుణకాలను సమానం చేయండి
6 = -4A ⇒ A = \(\frac{-3}{2}\)
స్థిరపదాలు సమానం చేయండి.
A + B = 5
B = 5 – A = 5 + \(\frac{3}{2}\) = \(\frac{13}{2}\)

ప్రశ్న 3.
∫\(\frac{d x}{4+5 \sin x}\) (Mar. 05)
సాధన:

ప్రశ్న 4.
∫\(\frac{1}{2-3 \cos 2 x}\) dx
సాధన:
t = tan x ⇒ dt = sec² x dx
= (1 + tan²x) dx
= (1 + t²) dx
dx = \(\frac{d t}{1+t^2}\)

ప్రశ్న 5.
∫x \(\sqrt{1+x-x^2}\) dx
సాధన:
x = A(1 – 2x) + B అనుకుందాం
x గుణకాలు సమానం చేయండి
1 = -2A ⇒ A = –\(\frac{1}{2}\)
స్థిరపదాలు సమానం చేయండి
0 = A + B ⇒ B = -A = \(\frac{1}{2}\)

ప్రశ్న 6.
∫\(\frac{d x}{(1+x) \sqrt{3+2 x-x^2}}\) (May 05)
సాధన:

ప్రశ్న 7.
∫\(\frac{d x}{4 \cos x+3 \sin x}\) (Mar. 06)
సాధన:

ప్రశ్న 8.
∫\(\frac{1}{\sin x+\sqrt{3} \cos x}\) dx
సాధన:

ప్రశ్న 9.
∫\(\frac{d x}{5+4 \cos 2 x}\) (Mar. 11)
సాధన:
t = tan x ⇒ dt = sec²x dx

ప్రశ్న 10.
∫\(\frac{2 \sin x+3 \cos x+4}{3 \sin x+4 \cos x+5}\) dx (Mar. 11) (A.P.Mar. 17) (A.P.Mar. 16) (T.S.Mar. 16)
సాధన:
2 sin x + 3 cos x + 4 = A(3 sin x + 4 cos x + 5) + B(3 cos x – 4 sin x) + C అనుకో౦డి.
sin x, గుణకాలు సమానం చేయు 3A – 4B = 2
cos x, గుణకాలు సమానం చేయు 4A + 3B = 2


(1) లో ప్రతిక్షేపించగా
I = \(\frac{18}{25}\) . x + \(\frac{1}{25}\) log |3 sin x + 4 cos x + 5| – \(\frac{4}{5\left(3+\tan \frac{x}{2}\right)}\) + C

ప్రశ్న 11.
∫\(\sqrt{\frac{5-x}{x-2}}\)dx, x ∈ (2, 5)
సాధన:

సజాతీయ పదాల గుణకాలు సమానం చేయగా
-2A = -1 ⇒ A = \(\frac{1}{2}\)
7A + B = 5

ప్రశ్న 12.
∫\(\sqrt{\frac{1+x}{1-x}}\) dx, x ∈ (-1, 1).
సాధన:

ప్రశ్న 13.
∫\(\frac{d x}{(1+x) \sqrt{3+2 x-x^2}}\), x ∈ (-1, 3).
సాధన:

ప్రశ్న 14.
∫\(\frac{d x}{(x+2) \sqrt{x+1}}\), x ∈ (-1, ∞).
సాధన:

ప్రశ్న 15.
∫\(\frac{d x}{(2 x+3) \sqrt{x+2}}\), x ∈ I ⊂ (-2, ∞) \ \(\left\{\frac{-3}{2}\right\}\).
సాధన:
x + 2 = t² ⇒ dx = 2t dt మరియు
2x + 3 = 2(t² – 2) + 3 = 2t² – 1

ప్రశ్న 16.
∫\(\frac{1}{(1+\sqrt{x}) \sqrt{x-x^2}}\) dx, x ∈ (0, 1).
సాధన:
∫\(\frac{1}{(1+\sqrt{x}) \sqrt{x-x^2}}\) dx
ప్రతిక్షేపించగా x = t² ⇒ dx = 2t dt

ప్రశ్న 17.
∫\(\frac{d x}{(x+1) \sqrt{2 x^2+3 x+1}}\), x ∈ I ⊂ R \ [-1, \(\frac{-1}{2}\)]
సాధన:

ప్రశ్న 18.
∫\(\sqrt{e^x-4}\) dx, x ∈ [log_e 4, ∞)
సాధన:

ప్రశ్న 19.

సాధన:

ప్రశ్న 20.
∫\(\frac{d x}{1+x^4}\), x ∈ R.
సాధన:

Students can go through AP Inter 2nd Year Physics Notes 12th Lesson వికిరణం, ద్రవ్యాల ద్వంద్వ స్వభావం will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 12th Lesson వికిరణం, ద్రవ్యాల ద్వంద్వ స్వభావం

→ కాథోడ్ కిరణాలు ఎలక్ట్రాన్లను కలిగి ఉండును. ఇవి రుణాత్మక ఆవేశ కణాలు.

→ J.J. థామ్సన్ ఎలక్ట్రాను కనుగొన్నాడు.

→ విశిష్టావేశం : ఆవేశం మరియు ద్రవ్యరాశికి గల నిష్పత్తిని విశిష్టావేశం అంటారు.
విశిష్టావేశం = e/m.S.I. పద్ధతిలో ప్రమాణం కులూంబ్/కి.గ్రా.

→ ఎలక్ట్రాన్ వోల్ట్ : ఒక ఎలక్ట్రాన్ 1 వోల్ట్ పొటెన్షియల్ తేడా గల బిందువుల మధ్య ఎలక్ట్రాన్ త్వరణం చెందినపుడు పొందు గతిజశక్తిని ఎలక్ట్రాన్ వోల్ట్ అంటారు.
1 ev = 1.6 × 10^-19 J.

→ విద్యుత్ క్షేత్రం వల్ల ఎలక్ట్రాన్పై బలం F = Ee.

→ అయస్కాంత క్షేత్రంనకు లంబంగా చలించే ఎలక్ట్రాన్పై బలం F

→ ఎలక్ట్రాన్ ఆవేశంను మిల్లికాన్ ఖచ్చితంగా నిర్ధారించారు.

→ ఎలక్ట్రాన్ ఆవేశం e = 1.6 × 10^-19 C మరియు ఎలక్ట్రాన్ ద్రవ్యరాశి m = 9.1 × 10^-31 kg.

→ ఒక ఏకరీతి విద్యుత్ క్షేత్రంలో గురుత్వాకర్షణ వలన స్వేచ్ఛగా క్రిందికి పడే ఆవేశపూరితమైన తైల బిందువు. చలనంను అధ్యయనం చేసి మిల్లికాన్ ఎలక్ట్రాన్ ఆవేశంను కనుగొన్నాడు.

→ లోహతలంపై తగినంత పౌనఃపున్యం ఉన్న వికిరణం పతనమయినపుడు, ఆ తలం నుంచి ఎలక్ట్రాన్లు ఉద్గారమవుతాయి. ఈ దృగ్విషయంను కాంతి విద్యుత్ ఫలితం అంటారు.

→ ఉద్గార ఎలక్ట్రాన్లను ఫోటో ఎలక్ట్రాన్లు అంటారు.

→ ఎలక్ట్రాన్లను ఉద్గారించు లోహాలను కాంతి లోహాలు అంటారు.
ఉదా : లిథియం, సోడియం, పొటాషియం.

→ నిరోధక పొటెన్షియల్ : ఎలక్ట్రాన్ నిరోధక పొటెన్షియల్ V అయితే, ఎలక్ట్రాన్ శక్తి Ve.
నిరోధక పొటెన్షియల్ పతన కిరణ తీవ్రతపై ఆధారపడదు.

→ క్వాంటం శక్తి E = hv = \(\frac{\mathrm{hc}}{\lambda}\)

→ ఐన్స్టీన్ ఫోటో విద్యుత్ ఫలిత సమీకరణము, hv = \(\frac{1}{2}\)mv² + Φ₀

→ ఫోటో విద్యుత్ ఘటాలు, ఫోటో విద్యుత్ ఫలిత అనువర్తనాలు.

→ కాంతి గుణకారి చాలా బలహీన కాంతి సంకేతాలను వృద్ధిపరచు సాధనం.

→ వేగంగా చలించే ఎలక్ట్రాన్లను లోహాలు ఆకస్మికంగా ఆపితే X-కిరణాల ఉత్పత్తి మరియు హెచ్చు ఉష్ణం వెలువడును.

→ లోహ తలం నుండి ఎలక్ట్రాన్ తప్పించుకుని బయటకు రావటానికి కావల్సిన కనీస శక్తిని, పని ప్రమేయం (Φ₀) అంటారు.

→ ప్లాటినమ్ పని ప్రమేయము ఎక్కువ (Φ₀ = 5.65 eV). సీజియంకు తక్కువ (Φ₀ = 2.14 eV).

→ ఒక లోహ ఉపరితలంపై తగినంత పౌనఃపున్యం ఉన్న కాంతి పతనం అయితే, ఎలక్ట్రాన్లు ఉద్గారమగును. ఈ వెలువడిన ఎలక్ట్రాన్లను ఫోటో ఎలక్ట్రాన్లు అంటారు. ఈ ప్రక్రియను కాంతి విద్యుత్ ఉద్గారం అంటారు.

→ లోహ ఉపరితలం నుంచి ఎలక్ట్రాన్ బయటకు రావడానికి పతన వికిరణానికి ఉండవలసిన కనీస పౌనః పున్యాన్ని ఆరంభ పౌనఃపున్యం (v₀) అంటారు.

→ హైసన్ బర్గ్ అనిశ్చితత్వ సూత్రం : “ఒకే సమయంలో ఖచ్చితంగా, ఒక ఎలక్ట్రాన్ స్థానం మరియు ద్రవ్యవేగంను కొలుచుట అసాధ్యం i.e. Δx Δp = h.

→ నిరోధక పొటెన్షియల్ మరియు గరిష్ట గతిజ శక్తుల మధ్య సంబంధం ev₀ = \(\frac{1}{2}\)mV_max² లేక V₀ ∞ mV_max²

→ శక్తి, E = hv = \(\frac{\mathrm{hc}}{\lambda}\)

→ ద్రవ్యవేగం, P = \(\frac{\mathrm{hv}}{\mathrm{c}}=\frac{\mathrm{h}}{\lambda}\)

→ ఐన్ స్టీన్ ఫోటో విద్యుత్ సమీకరణము
hv = hv₀ + = mv_max²; \(\frac{1}{2}\) = W + \(\frac{1}{2}\)mυ_max²

→ తరంగదైర్ఘ్యం λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\)

→ ద్రవ్యరాశి చలనంలో, m = \(\frac{\mathrm{m}_0}{\sqrt{1-\frac{v^2}{\mathrm{c}^2}}}\)

→ λ = \(\frac{12.27}{\sqrt{\mathrm{V}}}\)nm

→ λ = \(\frac{h}{p}=\frac{h}{m v}=\frac{h}{\sqrt{2 m E}}=\frac{h}{\sqrt{2 m e V}}\)

Students can go through AP Inter 2nd Year Physics Notes 11th Lesson విద్యుదయస్కాంత తరంగాలు will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 11th Lesson విద్యుదయస్కాంత తరంగాలు

→ విద్యుత్ వలయంలో కొంత భాగంలో కాలంతో పాటు విద్యుత్ ప్రవాహంలో మార్పురేటు వల్ల జనించే విద్యుత్ను స్థానభ్రంశ విద్యుత్ ప్రవాహం అంటారు.

→ విద్యుదయస్కాంత తరంగాలలో విద్యుత్ మరియు అయస్కాంతక్షేత్రాలు పరస్పరం లంబంగా కాలంతో మారుతూ తరంగ ప్రసార దిశకు పరస్పరం లంబంగా ఉంటాయి.

→ విద్యుదయస్కాంత తరంగాలను సైద్ధాంతికంగా మాక్స్వెల్ గుర్తించాడు.

→ ఆంపియర్ వలయనియమాన్ని మాక్స్వెల్ సవరించాడు.

→ మాక్స్వెల్ సమీకరణాలు స్థిరవిద్యుత్ గాస్ నియమం, అయస్కాంతత్వములో గాన్ నియమం, విద్యుదయస్కాంత ప్రేరణలో ఫారడే నియమం మరియు ఆంపియర్ వలయనియమం.

→ హెర్ట్ మరియు కొందరు సైంటిస్టులు ప్రయోగ పూర్వకంగా విద్యుదయస్కాంత తరంగాలను ఉత్పత్తి చేసి, అధ్యయనం చేశారు.

→ విద్యుదయస్కాంత తరంగాలు తిర్యక్ స్వభావాన్ని కలిగి ఉంటాయి.

→ విద్యుదయస్కాంత తరంగాల వేగం, కాంతి వేగానికి సమానం.

→ త్వరణం చెందే ఆవేశాలు విద్యుదయస్కాంత తరంగాలను జనింపజేస్తాయి.

→ విద్యుదయస్కాంత తరంగాల పౌనఃపున్యము (లేదా) తరంగదైర్ఘ్య మొత్తం అవధిని విద్యుదయస్కాంత వర్ణపటం అంటారు.

→ స్థానభ్రంశ విద్యుత్ (i_D) = ε₀\(\frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\)

→ ఆంపియర్ వలయ నియమం, \(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d}} \ell\) = μ₀(i₀ + ε₀ \(\frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\))

→ మాక్స్వెల్ సమీకరణాలు

• \(\oint \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}\) = q/ε₀ (స్థిరవిద్యుత్ గాస్ నియమం.)
• \(\oint \vec{B} \cdot \overrightarrow{d s}\) = 0 (అయస్కాంతత్వములో గాస్ నియమం.)
• \(\int \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{d} \ell}=\frac{-\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) (విద్యుదయస్కాంత ప్రేరణలో ఫారడే నియమం.)
• \(\int \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{d} \ell}\) = μ₀ (i₀ + ε₀\(\frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\))

→ కాంతి వేగము (C) = \(\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\) = 3 × 10⁸ m/s

→ వక్రీభవన గుణకం (μ) = \(\frac{\mathrm{C}}{\mathrm{V}}=\sqrt{\frac{\mathrm{i} \varepsilon}{\mathrm{i}_0 \varepsilon_0}}\)

→ విద్యుత్ క్షేత్రం యొక్క శక్తి సాంద్రత (U_E) = \(\frac{1}{2}\)ε₀E²

→ అయస్కాంతక్షేత్రం యొక్క శక్తి సాంద్రత (U_B) = \(\frac{\mathrm{B}^2}{2 \mu_0^2}\)

→ పాయింటింగ్ సదిశ \((\overrightarrow{\mathrm{P}})=\frac{1}{\mu_0}(\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{B}})\)

→ విద్యుదయస్కాంత తరంగాల తీవ్రత (I) = \(\frac{1}{2}\)ε₀CE₀²

→ పీడనం (P)

Students can go through AP Inter 2nd Year Physics Notes 10th Lesson ఏకాంతర విద్యుత్ ప్రవాహం will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 10th Lesson ఏకాంతర విద్యుత్ ప్రవాహం

→ ఏకాంతర విద్యుత్ ప్రవాహం అనగా కాలంతోపాటు పరిమాణం మారుతూ మరియు ఆవర్తనంగా దిశ మారుతుంది.

→ A.C యొక్క సగటు విలువ (లేదా) సరాసరి విలువ నిలకడ విద్యుత్ ప్రవాహానికి సమానం. అదే వలయంలో, అదే కాలంలో ఏకాంతర విద్యుత్ ప్రవాహము, అంటే మొత్తం ఆవేశాన్ని అందిస్తుంది.

→ ఒక పూర్తి భ్రమణం (లేదా) ఆవర్తనంలో తక్షణ ప్రవాహ వర్గాల సరాసరి విలువ వర్గ మూలాన్నిms. విలువ అంటారు.

→ నిరోధం గుండా a.c నింపినప్పుడు వోల్టేజి, విద్యుత్ ప్రవాహము ఒకే దశలో ఉంటాయి.

→ ప్రేరకం గుండా a.c ని పంపినప్పుడు, విద్యుత్ ప్రవాహంకన్నా వోల్టేజి \(\frac{\pi}{2}\) (లేదా) 90° ముందుంటుంది.

→ కెపాసిటర్గుండా a.c ని పంపినప్పుడు, విద్యుత్ ప్రవాహంకన్నా వోల్టేజి \(\frac{\pi}{2}\) (లేదా) 90′

→ ప్రేరకంగుండా a.c ని పంపినప్పుడు కలిగే నిరోధాన్ని ప్రేరకత్వ నిరోధము అంటారు. కెపాసిటర్గుండా a.c ని పంపినప్పుడు కలిగే నిరోధాన్ని కెపాసిటివ్ రియాక్టెన్స్ అంటారు. a.c వలయంలో ఓమిక్ నిరోధము వల్ల సామర్థ్య నష్టం జరుగుతుంది.

→ శుద్ధ ప్రేరక (లేదా) శుద్ధ కెపాసిటర్ వలయంలో సామర్థ్య కారకం ఉంటుంది.

→ పరివర్తకం అన్యొన్య ప్రేరకతపై ఆధారపడుతుంది.

→ పరివర్తకం a.c లో పనిచేస్తుంది మరియు d.c. లో పనిచేయదు.

→ ఏకాంతర అల్ప వోల్టేజి (అధిక విద్యుత్) నుండి అధిక వోల్టేజి (అల్ప విద్యుత్) కు మార్చుటకు పరివర్తకంను ఉపయోగిస్తారు.

→ తక్షణ వోల్టేజి మరియు తక్షణ విద్యుత్ ప్రవాహా లబ్ధమును తక్షణ సామర్థ్యం అంటారు.

→ ప్రేరకం (లేదా) కెపాసిటర్ వద్ద వోల్టేజికి, అనువర్తిత వోల్టేజికి గల నిష్పత్తిని Q-కారకం అంటారు.

→ అనునాద కోణీయ పౌనఃపున్యానికి, పట్టీ వెడల్పుకుగల నిష్పత్తిని అనునాద నైశిత్యం అంటారు.

→ వేష్టన చుట్టను ఉపయోగించి విద్యుత్ సామర్థ్యం నష్టం లేకుండా a.c ని నియంత్రిస్తుంది.

→ జనరేటర్లు మరియు మోటార్లలో నివేశనం మరియు నిర్గమనాలు తారమారవుతాయి.

→ మోటార్ విద్యుత్ శక్తి నివేశనం మరియు యాంత్రికశక్తి నిర్గమనం.

→ జనరేటర్లో యాంత్రికశక్తి నివేశనం మరియు విద్యుత్ శక్తి నిర్గమనం.

→ ఏకాంతర విద్యుత్ ప్రవాహం మరియు వోల్టేజి i = i_m sin ot మరియు υ = v₀ sin ot

→ V_rms = \(\frac{V_m}{\sqrt{2}}\) మరియు i_rms = \(\frac{\mathrm{i}_0}{\sqrt{2}}\)

→ ఇండక్టివ్ రియాక్టెన్స్ (X_L) = ωL

→ కెపాసిటివ్ రియాక్టెన్స్ (X_C) = \(\frac{1}{\omega \mathrm{C}}\)

→ అవరోధము (Z) = \(\sqrt{R^2+\left(\frac{1}{\omega C}-\omega L\right)^2}=\sqrt{R^2+\left(X_C-X_L\right)^2}\)

→ Φ = tan^-1\(\left(\frac{\frac{1}{\omega C}-\omega L}{R}\right)\) = tan^-1\(\left[\frac{\mathrm{X}_{\mathrm{C}}-\mathbf{X}_{\mathrm{L}}}{\mathrm{R}}\right]\)

→ f₀ = \(\frac{1}{2 \pi \sqrt{L C}}\)

→ Q- కారకం = \(\frac{\omega_0 \mathrm{~L}}{\mathrm{R}}=\frac{1}{\omega_0 \mathrm{CR}}\)

→ సగటు సామర్థ్యం (p) = V_rms × I_rms × cos Φ

→ పరివర్తకం నిష్పత్తి = \(\frac{N_s}{N_p}=\frac{V_s}{V_p}\)

Students can go through AP Inter 2nd Year Physics Notes 9th Lesson విద్యుదయస్కాంత ప్రేరణ will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 9th Lesson విద్యుదయస్కాంత ప్రేరణ

→ మారే అయస్కాంత క్షేత్రము, విద్యుత్ క్షేత్రాన్ని జనింపచేస్తుంది.

→ వాహకంలో మొత్తం బలరేఖల సంఖ్యను అయస్కాంత అభివాహం అంటారు.

→ ఫారడే ప్రయోగాల ద్వారా విద్యుదయస్కాంత ప్రేరణ దృగ్విషయం ఆవిష్కరించబడినది.

→ తీగచుట్టలో అయస్కాంత అభివాహం మారితే, దానిలో విద్యుచ్ఛాలక బలం ప్రేరితమవుతుంది.

→ ప్రేరిత విద్యుచ్ఛాలక బలం, అయస్కాంత అభివాహంలో మార్పు రేటుకు అనులోమానుపాతంలో ఉంటుంది.

→ లెంజ్ నియమం ప్రకారం ప్రేరిత వి.చా.బ దిశ ఎల్లప్పుడూ అధిగమించడానికి ఉపయోగపడిన దానిని వ్యతిరేకిస్తుంది.

→ మారు ప్రవాహాలు (లేదా) ఫోకాల్ట్ ప్రవాహాలు, వాహకంను మారే అయస్కాంత క్షేత్రంలో ఉంచినప్పుడు . ప్రేరితమయ్యే విద్యుత్ ప్రవాహం.

→ ఎడ్జీ ప్రవాహాలు ప్రాయోగిక అనువర్తనాలలో మరియు అవసరంలేని ప్రభావాలలో ఉపయోగిస్తారు.

→ నిరోధాల పెట్టెలలో స్వయం ప్రేరణను తొలగించడానికి ప్రేరకతలేని తీగచుట్టలను వాడతారు.

→ తీగ ప్రేరకంలాగా పనిచేయదు. అందుకు కారణం విస్మరించదగిన అడ్డుకోత వైశాల్యం గల తీగలో అయస్కాంత అభివాహం సున్నా

→ తీగచుట్టలాగా తీగను చుట్టితే, అది ప్రేరకం వలె పనిచేస్తుంది.

→ సాలినాయిడ్ పొడవు, దాని అడ్డుకోత వైశాల్యంతో పోల్చితే చాలా ఎక్కువ.

→ విద్యుదయస్కాంత ప్రేరణ నియమాలు :

• తీగచుట్టలో అయస్కాంత అభివాహం మారితే, వలయంలో విద్యుచ్ఛాలక బలం జనిస్తుంది.
• వలయంలో వి.చా.బ పరిమాణం, అయస్కాంత అభివాహంలో మార్పు రేటుకు అనులోమానుపాతంలో ఉంటుంది.

→ తీగచుట్టలో విద్యుత్ ప్రవాహము మారితే, అయస్కాంత అభివాహం మారి, దానిలో ప్రేరిత వి.చా.బ. జనిస్తుంది. ఈ దృగ్విషయాన్ని స్వయంప్రేరణ అంటారు.

→ ఒక తీగచుట్టలో విద్యుత్ ప్రవాహము మారితే, అయస్కాంత అభివాహం మారి, మరొక తీగచుట్టలో వి.చా.బ. ప్రేరితమవుతుంది. ఈ దృగ్విషయాన్ని అన్యోన్య ప్రేరణ అంటారు.

→ అయస్కాంత అభివాహం (Φ_B) = B.A = BA cos θ

→ ε = \(\frac{-\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)

→ ε = -N\(\frac{\mathrm{d} \phi}{\mathrm{dt}}\)

→ చలన వి.చా.బ. (ε) = Blυ.

→ ε = – L\(\frac{\mathrm{dI}}{\mathrm{dt}}\)

→ ε = -M₁₂\(\frac{\mathrm{dI}}{\mathrm{dt}}\)

→ అయస్కాంత క్షేత్రంలో నిల్వ ఉన్న శక్తి (u) = \(\frac{1}{2}\)LI₀²

→ సాలినాయిడ్ యొక్క స్వయం ప్రేరకత (L) = μ₀n²Al

→ రెండు పొడవైన సాలినాయిడ్ల యొక్క అన్యోన్య ప్రేరకత (M) = μ₀n¹n²Al

→ తక్షణ ప్రేరిత వి.చా.బ (ε) = NBAω sin ωt.

→ F= q\((\vec{E}+\vec{v} \times \vec{B})\)

→ సామర్థ్యము (p) = \(\frac{\mathrm{B}^2 l^2 v^2}{\mathrm{r}}\)

→ NΦ = LI.

→ NΦ = MI.

Students can go through AP Inter 2nd Year Physics Notes 8th Lesson అయస్కాంతత్వం-ద్రవ్యం will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 8th Lesson అయస్కాంతత్వం-ద్రవ్యం

→ సూదంటు రాయి ఒక సహజ అయస్కాంతం. ఇది మాగ్నటైట్ అనే ఇనుప ఖనిజము. సూదంటు రాయి అనగా దారి చూపించునది.

→ అయస్కాంతం యొక్క అయస్కాంత క్షేత్ర రేఖలు అవిచ్ఛిన్న సంవృత ఉచ్చులను ఏర్పరుచును.

→ విద్యుత్ ప్రవాహ ఉచ్చుతో ముడిపడి ఉన్న అయస్కాంత ద్విధ్రువ భ్రామకము m = NIA. ఇక్కడ ఉచ్చులో చుట్ల సంఖ్య N. I విద్యుత్ ప్రవాహము మరియు A సదిశ వైశాల్యం.

→ సాలినాయిడ్ అయస్కాంత భ్రామకం పరిమాణం m = n(2l) I (πa²)

→ ఒక దండాయస్కాంత అక్షీయ అయస్కాంత క్షేత్రము B_A = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{~m}}{\mathrm{r}^3}\)

→ ఏకరీతి అయస్కాంత క్షేత్రంలో ద్విధ్రువం (సూది) పై టార్క్ τ = m × B

→ ఒక దండాయస్కాంతం మధ్య లంబక్షేత్రము B_E = \(\frac{\mu_0}{4 \pi}\)

→ అయస్కాంతత్వంలో గాస్ నియమము : ఏదైనా సంవృత తలం ద్వారా నికర, అయస్కాంత అభివాహము సున్న, i.e. ∫_sB.ds = 0

→ అయస్కాంత ఉత్తర మరియు దక్షిణ దృవములను కలుపు ఊహారేఖ ద్వారా పోవు లంబతలంను, ఆ ప్రదేశంలో అయస్కాంత యామ్యోత్తర రేఖ అంటారు.

→ నిజ భౌగోళిక ఉత్తర ధృవము మరియు కంపాసు సూచి చూపు ఉత్తర ధృవమునకు మధ్య గల కోణంను దిక్పాతము అంటారు.

→ భూమి అయస్కాంత మొత్తం తీవ్రత తెలుపు దిశకు మరియు అయస్కాంత యామ్యోత్తర రేఖకు మధ్య కోణంను అవపాతము అంటారు..

→ ప్రమాణ ఘనపరిమాణంలో అయస్కాంత భ్రామకంను అయస్కాంతీకరణం అంటారు.

దీని ప్రమాణము Am^-1 మరియు దీని మితులు L^-1A.

→ 300K వద్ద, రుణ డయా అయస్కాంత పదార్థాలు బిస్మత్, రాగి, వజ్రము, బంగారము, సీసము, పాదరసము, నైట్రోజన్ (S.T.P), వెండి, సిలికాన్,

→ 300K వద్ద, ధన పారా అయస్కాంత పదార్థాలు అల్యూమినియం, కాల్షియం, క్రోమియం, లిథియం, మెగ్నీషియం, నియోబియమ్, ఆక్సిజన్ (STP), ప్లాటినమ్, టంగస్టన్.

→ డయా అయస్కాంత పదార్థాలకు, -1 ≤ χ < 0; 0 ≤ μ_r < 1; μ < μ₀.

→ పారా అయస్కాంత పదార్థాలకు, 0 < χ < ε, 1 < μ_r < 1 + ε; μ > μ₀.

→ ఫెర్రో అయస్కాంత పదార్థాలకు, χ >> 1; μ_r >> 1; μ < μ₀.

→ పారా అయస్కాంత అయస్కాంతీకరణము, పరమ ఉష్ణోగ్రత T.కు విలోమానుపాతంలో ఉండును.
M = \(\frac{\mu_0}{T}\) లేకు తుల్యంగా, χ = C\(\frac{\mu_0}{T}\)

→ పారా అయస్కాంత నమూనాపై, క్షేత్రం పెంచినా లేక ఉష్ణోగ్రత తగ్గించినా, అయస్కాంతీకరణ సంతృప్త విలువ Ms, చేరు వరకు పెరుగును. ఈ స్థితిలో ధృవాలన్నీ క్షేత్ర దిశలో పూర్తిగా అమరును.

→ ఫెర్రో అయస్కాంత పదార్థ సూక్ష్మ ఘనపరిమాణం (10^-6 cm³ నుండి 10^-2 cm³) ను డొమైన్ అంటారు.

→ డొమైన్ పరిమాణము 1mm మరియు డొమైన్లో పరమాణువుల సంఖ్య 10¹¹.

→ కొన్ని ఫెర్రో అయస్కాంత పదార్థాలలో అయస్కాంతీకరణ దృఢంగా ఉంటుంది. అటువంటి పదార్థాలను కఠిన అయస్కాంత పదార్థాలు లేక కఠిన ఫెర్రో అయస్కాంత పదార్థాలంటారు. ఫెర్రో అయస్కాంత పదార్థాలకు, μ_r > 1000.

→ ఫెర్రో అయస్కాంత పదార్థం, పారా అయస్కాంత పదార్థంగా మారు ఉష్ణోగ్రతను, క్యూరీ ఉష్ణోగ్రత T అంటారు.

→ I మరియు B లు H వెనక ఉండటాన్ని, శైథిల్యం అంటారు.

→ H = 0 వద్ద I విలువను రెటింటివిటి అంటారు.

→ H యొక్క తిరోదిశలో I ను సున్నాకు చేర్చుటకు కావాల్సిన అయస్కాంత బల విలువను కొయిర్సివిటి అంటారు.

→ విద్యుదయస్కాంతాలు, విద్యుత్ గంటలు, లౌడ్ స్పీకర్స్ మరియు టెలిఫోన్ డయఫ్రమ్స్ వాడతారు.

→ కూలుమ్ నియమము, F = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{m}_1 \mathrm{~m}_2}{\mathrm{r}^2}\) = 10^-7 × \(\frac{\mathrm{m}_1 \mathrm{~m}_2}{\mathrm{r}^2}\)

→ అయస్కాంత ద్విధ్రువం, \(\overrightarrow{\mathbf{M}}=\mathrm{m}(\overrightarrow{2 l})\)

→ విద్యుత్ లూపు అయస్కాంత భ్రామకము, \(\vec{M}=I \vec{A}\)

→ కక్ష్యా చలనం వల్ల అయస్కాంత భ్రామకము, μ_l = n\(\left(\frac{\mathrm{eh}}{4 \pi \mathrm{m}_{\mathrm{e}}}\right)\)

→ బోర్ మాగ్నిటాన్, μ_B = \(\frac{\mathrm{eh}}{4 \pi \mathrm{m}_{\mathrm{e}}}\)

→ పొట్టి ద్విధ్రువంకు,

→ \(\overrightarrow{\mathrm{B}_{\mathrm{e}}}=\frac{\mu_0}{4 \pi}=\frac{\overrightarrow{\mathrm{m}}}{\left(\mathrm{r}^2+l^2\right)^{3 / 2}}\) పొట్టి దండాయస్కాంతమునకు, B_e = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{m}}{\mathrm{r}^3}\)

→ ఏదైనా బిందువు వద్ద పొట్టి అయస్కాంత ద్విధ్రువం వల్ల అయస్కాంత క్షేత్రము B = \(\frac{\mu_0}{4 \pi} \frac{M \sqrt{3 \cos ^2 \theta+1}}{\mathbf{r}^3}\)

→ టార్క్ \(\vec{\tau}=\overrightarrow{\mathrm{m}} \times \overrightarrow{\mathrm{B}}\)

→ అయస్కాంత క్షేత్రంలో ఒక దండాయస్కాంతమును ఉంచినపుడు స్థితిజ శక్తి U = -m B cos θ = –\(\overrightarrow{\mathrm{m}} \times \overrightarrow{\mathrm{B}}\)

→ అయస్కాంతత్వంలో గాస్ నియమము \(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{ds}}\)

→ అయస్కాంత తీవ్రత H = \(\frac{B_0}{\mu_0}\)

→ అయస్కాంతీకరణ తీవ్రత I = \(\frac{\mathrm{M}}{\mathrm{V}}=\frac{\mathrm{m} \times 2 l}{\mathrm{~A} \times 2 l}=\frac{\mathrm{m}}{\mathrm{A}}\)

→ అయస్కాంత అభివాహం Φ = \(\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\Delta \mathrm{s}}\)

→ అయస్కాంత ససెప్టిబిల్టి χ_m = \(\frac{I}{H}\)

→ అయస్కాంత పర్మియబిల్టి μ = \(\frac{\mathrm{B}}{\mathrm{H}}\)

→ μ = μ₀ (1 + χ_m) మరియు μ_r = 1 + χ_m

→ క్యూరీ నియమము χ_m α \(\frac{1}{T}\) ⇒ χ_m = T స్థిరాంకం.

Students can go through AP Inter 2nd Year Physics Notes 7th Lesson చలించే ఆవేశాలు-అయస్కాంతత్వం will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 7th Lesson చలించే ఆవేశాలు-అయస్కాంతత్వం

→ అయస్కాంత క్షేత్రం ఎల్లప్పుడూ, విద్యుత్ ప్రవాహంతో కలిసి ఉంటుంది.

→ సౌష్ఠవ విద్యుత్ ప్రవాహ వితరణ ఉన్నప్పుడు మాత్రమే బయోట్-సవర్ట్ నియమం పాటించబడుతుంది.

→ విద్యుత్ ప్రవాహ వాహకం చుట్టూ ఏర్పడే అయస్కాంత క్షేత్రము ఏకరీతిగా ఉండదు. కాని ప్రయోగ అవసరాల కోసం దాని కేంద్రం వద్ద ఏకరీతిగా తీసుకుంటాం.

→ నిశ్చిలస్థితిలో విద్యుదావేశాలు స్థిర విద్యుత్ అంతర చర్యలను చలనంలో ఉన్న ఆవేశాలు అయస్కాంత అంతర చర్యలను ఏర్పరచును.

→ అయస్కాంత బలం, విద్యుత్ బలం కన్నా స్వల్పం.

→ డోలన మరియు త్వరణం చెందే ఆవేశాలు విద్యుదయస్కాంత తరంగాలను జనింపచేస్తాయి.

→ విద్యుత్ మరియు అయస్కాంత క్షేత్రాలు ఉన్నప్పుడు, అంతరాళంలో చలించే ఆవేశంపై పనిచేసే బలాన్ని లారెంజ్ బలం అంటారు.

→ అయస్కాంత క్షేత్రం (B) యొక్క రేఖీయ సమాకలని, సంవృత వలయంలో మొత్తం విద్యుత్ ప్రవాహం (i) కు
μ₀ రెట్లుంటుంది. ∮\(\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = μ₀I

→ అవసరమైన అయస్కాంతక్షేత్రాన్ని జనింపచేయడానికి టెలివిజన్లో సాలినాయిడ్ను వాడతారు.

→ టోరాయిడ్ అనగా బోలుగా ఉండే వృత్తాకార రింగ్, దీనిలో విద్యుత్ బంధిత తీగ అనేకచుట్లు దగ్గర దగ్గరగా చుట్టబడి ఉంటుంది.

→ బయోట-సవర్ట్ నియమంను ఇలా తెలుపవచ్చు. \(\overrightarrow{\mathrm{dB}}=\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}=\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \times \overrightarrow{\mathrm{r}}}{\mathrm{r}^3}\)

→ రెండు తిన్నని సమాంతర వాహకాలలో విద్యుత్ ప్రవాహాలు ఒకే దిశలో ఉంటే అవి పరస్పరం ఆకర్షించుకుంటాయి మరియు విద్యుత్ ప్రవాహాలు వ్యతిరేక దిశలలో ఉంటే వికర్షించుకుంటాయి.

→ సైక్లోట్రాన్ ఎలక్ట్రాన్లు మరియు న్యూట్రాన్లను త్వరణం చెందించదు.

→ అమ్మీటరును వలయాలలో ఎల్లప్పుడూ శ్రేణిలోనే కలుపుతారు.

→ వోల్టు మీటరును వలయాలలో ఎల్లప్పుడూ సమాంతరంగానే కలపాలి.

→ ఆదర్శ అమ్మీటరు నిరోధము సున్నా.

→ ఆదర్శ వోల్టు మీటరు నిరోధము అనంతం

→ N చుట్లు, A వైశాల్యం గల తీగచుట్టలో విద్యుత్ ప్రవాహం i అయిన అయస్కాంత భ్రామకం (m)m = NiA

→ కేంద్రకం చుట్టూ తిరిగే ఎలక్ట్రాన్ యొక్క అయస్కాంత భ్రామకం μ_l = \(\frac{\mathrm{e}}{2 \mathrm{~m}}\)l

→ పరస్పరం లంబంగా ఉన్న విద్యుత్ మరియు అయస్కాంత క్షేత్రాల గుండా అంతరాళంలో ఒక గల ఆవేశిత కణాల కిరణపుంజము యొక్క ఎంపికను వేగవరణకం అంటారు.

→ F = q (\(\vec{v} \times \vec{B}\)) (లేదా) F = Bqv sin θ

→ dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)

→ B = \(\frac{\mu_0 n i^2}{2\left(r^2+x^2\right)^{3 / 2}}\)

→ B = \(\frac{\mu_0 n i^2}{2\left(r^2+x^2\right)^{3 / 2}}\)

→ B = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{i}}{\mathrm{a}}\)(sin Φ₁ + sin Φ₂)

→ B = \(\frac{\mu_0 \mathbf{i}}{2 \pi \mathrm{a}}\)

→ M = niA

→ B = μ₀ni (సాలినాయిడ్ కేంద్రం వద్ద)

→ B = \(\frac{\mu_0 n i}{2}\)(సాలినాయిడ్ ఒక చివర వద్ద)

→ ∮\(\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = μ₀I

→ F = q\([\overrightarrow{\mathbf{E}}+(\vec{v} \times \overrightarrow{\mathbf{B}})]\)

→ F = i\((\vec{l} \times \vec{B})\) = Bil sin θ

→ τ = \(\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}\) = MB sin θ

→ i = \(\frac{\mathrm{C}}{\text { BAN }}\)θ

→ S = \(\frac{i_g G}{i-i_g}\)

→ R = \(\frac{\mathrm{v}}{\mathrm{i}_{\mathrm{g}}}\) – G

→ F = \(\frac{\mu_0 i_1 i_2 l}{2 \pi r}\)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 7 నిశ్చిత సమాకలనులు Exercise 7(d) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 7 నిశ్చిత సమాకలనులు Exercise 7(d)

అభ్యాసం – 7 (డి)

I. క్రింద ఇచ్చిన వక్రాలతో ఆవృతమైన ప్రదేశం వైశాల్యం కనుక్కోండి.

ప్రశ్న 1.
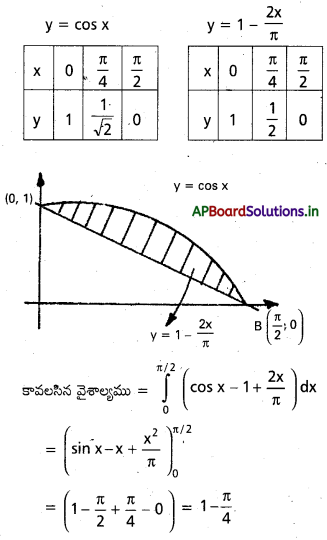
y = cos x, y = 1 – \(\frac{2 \mathbf{x}}{\pi}\) (Mar. ’05)
సాధన:
దత్త వక్రాల సమీకరణాలు
y = cos x —- (1)
y = 1 – \(\frac{2 x}{\pi}\) — (2)
(1), (2) ల నుండి y ను తొలగించగా
cos x = 1 – \(\frac{2 x}{\pi}\)
అయితే x = \(\frac{\pi}{2}\), cos x = cos \(\frac{\pi}{2}\) = 0
1 – \(\frac{2}{\pi}\) . x = 1 – \(\frac{2}{\pi}\) . \(\frac{\pi}{2}\) = 1 – 1 = 0
అయితే x = 0, cos x = cos 0 = 1
1 – \(\frac{2 x}{\pi}\) = 1 – 0 = 1
∴ ఖండన బిందువులు A(0, 1), B(\(\frac{\pi}{2}\), 0)

ప్రశ్న 2.
y = cos x, y = sin 2x, x = 0, x = \(\frac{\pi}{2}\).
సాధన:

కావలసిన వైశాల్యము

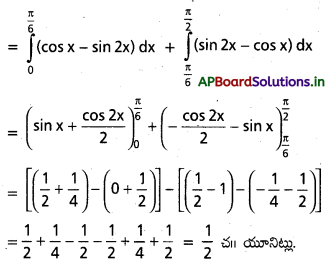
ప్రశ్న 3.
y = x³ + 3, y = 0, x = -1, x = 2 (Mar. 05)
సాధన:
PABQ వైశాల్యము

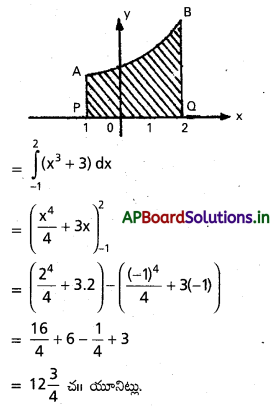
ప్రశ్న 4.
y = e^x, y = x, x = 0, x = 1
సాధన:

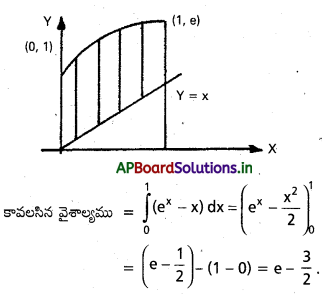
ప్రశ్న 5.
y = sin x, y = cos x, x = 0, x = \(\frac{\pi}{2}\)
సాధన:

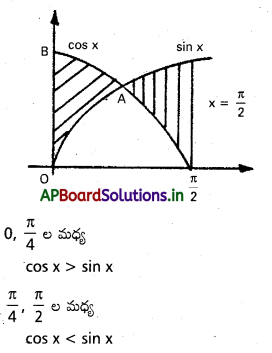
కావలసిన వైశాల్యము

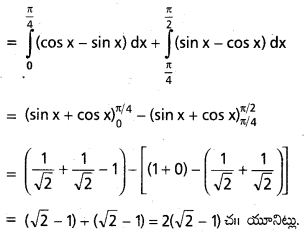
ప్రశ్న 6.
x = 4 – y², x = 0
సాధన:
x = 4 – y² పరావలయం, x – అక్షాన్ని A (4, 0) వద్ద y – అక్షాన్ని P (0, 2) మరియు Q (0, – 2) వద్ద ఖండిస్తుంది. పరావలయం x-అక్షం దృష్ట్యా సౌష్టవము

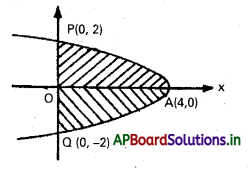
కావలసిన వైశాల్యము = 2 వైశాల్యం OAP
= 2\(\int_0^2\)(4 – y²) dy
= 2\(\left(4 y-\frac{y^3}{3}\right)_0^2\)
= 2\(\left(8-\frac{8}{3}\right)\)
= 2.\(\frac{16}{3}\) = \(\frac{32}{3\) చ|| యూనిట్లు,

ప్రశ్న 7.
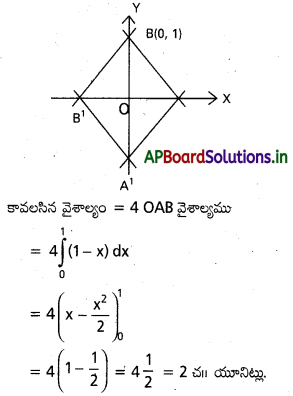
|x| + |y| = 1 వక్రంతో ఆవృత్తమైన వైశాల్య౦ కనుక్కోండి.
సాధన:

II.

ప్రశ్న 1.
x = 2 – 5y – 3y², x = 0.
సాధన:
దత్త సమీకరణాలను సాధించగా
2 – 5y – 3y² = 0
3y² + 5y – 2 = 0
(y + 2) (3y – 1) = 0 y = -2 or \(\frac{1}{3}\)

ప్రశ్న 2.
x² = 4y, x = 2, y = 0
సాధన:

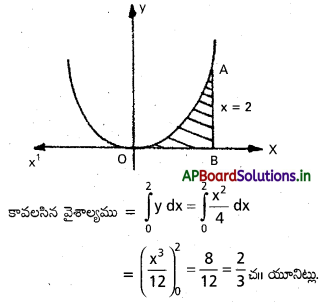
ప్రశ్న 3.
y² = 3x, x = 3.
సాధన:

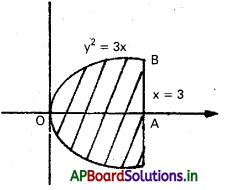
పరావలయం X – అక్షం దృష్ట్యా సౌష్ఠవము
కావలసిన వైశాల్యము = \(2 \int_0^3 \sqrt{3} \cdot \sqrt{x} d x\)
= \(\left(2 \sqrt{3} \cdot \frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right)_0^3\)
= \(\frac{4 \sqrt{3}}{3}\).(3\(\sqrt{3}\) – 0)
= 12 చ|| యూనిట్లు

ప్రశ్న 4.
y = x², y = 2x.
సాధన:
దత్త సమీకరణాలు
y = x² —– (1)
y = 2x —– (2)

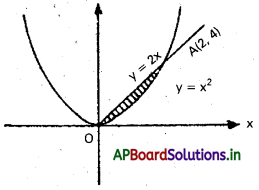
y ను తొలగించగా x² = 2x
x² – 2x = 0
x(x – 2) = 0
x = 0 or x = 2
y = 0, or y = 4
ఖండన బిందువులు O(0, 0), A(2, 4)
కావలసిన వైశాల్యము = \(\int_0^2\left(2 x-x^2\right) d x\)
= \(\left(x^2-\frac{x^3}{3}\right)_0^2\) = 4 – \(\frac{8}{3}\)
= \(\frac{4}{3}\) చ॥ యూనిట్లు.

ప్రశ్న 5.
y sin 2x, y = \(\sqrt{3}\) sin x, x = 0, x = \(\frac{\pi}{6}\)
సాధన:
దత్త సమీకరణాలు y = sin 2x —– (1)
y = \(\sqrt{3}\) sin x —- (2)
sin 2x = \(\sqrt{3}\) sinx
2 sin x cos x = \(\sqrt{3}\) sin x
sin x = 0 లేదా 2 cos x = \(\frac{\sqrt{3}}{2}\)
x = 0 cos x = \(\frac{\sqrt{3}}{2}\) ⇒ x = \(\frac{\pi}{6}\)

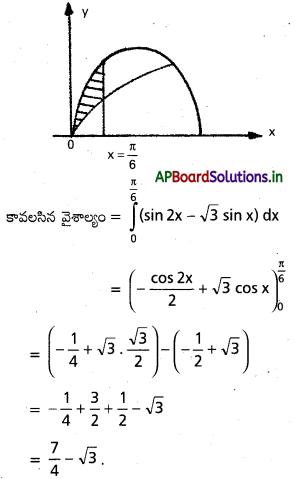
ప్రశ్న 6.
y = x², y = x³.
సాధన:
దత్త సమీకరణాలు y = x² —– (1)
y = x³ —- (2)

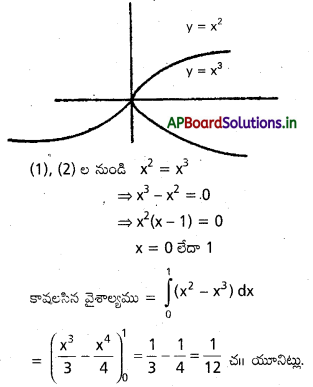
ప్రశ్న 7.
y = 4x – x², y = 5 – 2x [T.S. Mar. 16]
సాధన:

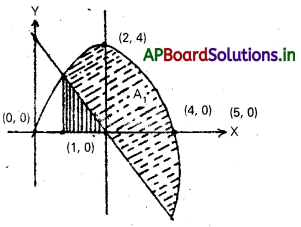
y = 4x – x² —- (1)
y = 5 – 2x —– (2)
y = -([x – 2]²) + 4
y – 4 = -(x – 2)²
(i), (ii) లను సాధించగా
4x – x² = 5 – 2x
x² – 6x + 5 = 0
(x – 5) (x – 1) = 0
x = 1, 5
కావలసిన వైశాల్యం = \(\int_1^5\)(4x – x² – 5 + 2x) dx
= \(\int_1^5\) (6x – x² – 5) dx

ప్రశ్న 8.
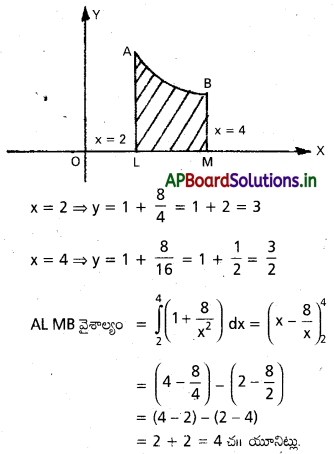
X – అక్షం, y = 1 + \(\frac{8}{x^2}\) వక్రభాగం, x = 2, x = 4 రేఖలతో పరిబద్ధమైన వైశాల్యం కనుక్కోండి.
సాధన:
దత్త సమీకరణాలు y = 1 + \(\frac{8}{x^2}\)

ప్రశ్న 9.
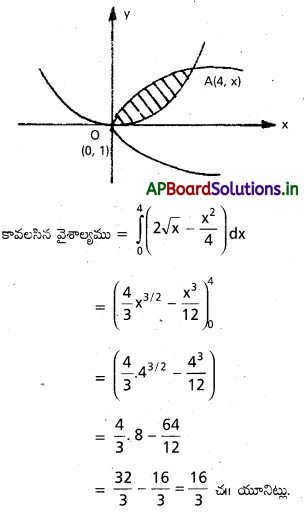
పరావలయాలు y² = 4x, x² = 4y లతో పరిబద్ధమైన ప్రదేశం వైశాల్యం కనుక్కోండి.
సాధన:
వక్రాల సమీకరణాలు
y² = 4x —- (1)
x² = 4y —– (2)
\(\left(\frac{x^2}{4}\right)^2\) = 4x
\(\frac{x^4}{16}\) = 4x
x⁴ = 64 ⇒ x⁴ = 0 లేదా x³ = 64, x = 4

ప్రశ్న 10.
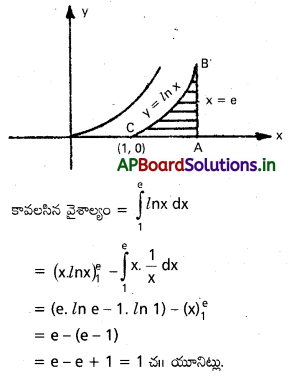
వక్రం y = lnx, X – అక్షం, సరళరేఖ x = e లతో పరిబద్ధమైన వైశాల్యం కనుక్కోండి.
సాధన:
వక్రం సమీకరణము y = lnx
x = 1 ⇒ y = 0
వక్రం y = lnx
X – అక్షాన్ని c(1, 0) వద్ద ఖండిస్తుంది.

III.

ప్రశ్న 1.
y = x² + 1, y = 2x – 2, x = -1, x = 2. వక్రాల మధ్య వైశాల్యం ఎంత ?
సాధన:
దత్త సమీకరణాలు
y = x² + 1 —– (1)
y = 2x – 2 —- (2)

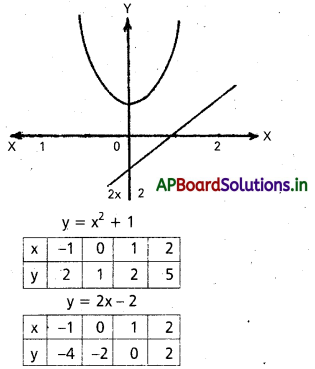
దత్త రేఖల మధ్య వైశాల్యము

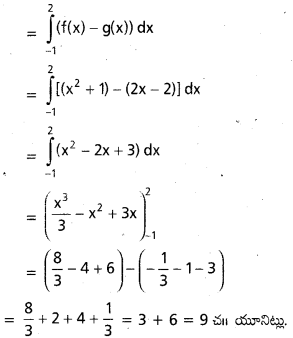
ప్రశ్న 2.
y² = 4x, y² = 4(4 – x) వక్రాల మధ్య వైశాల్యం ఎంత ? (May ’11)
సాధన:
వక్రాల సమీకరణాలు y² = 4x —- (1)
y² = 4(4 – x) —- (2)
y ను తొలగించగా
4x = 4 (4 – x)
2x = 4 ⇒ x = 2
(1) లో ప్రతిక్షేపించగా y² = 8
y = ±2\(\sqrt{2}\)

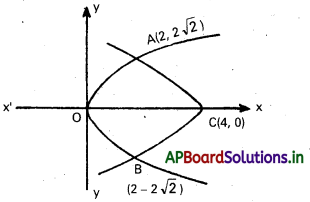
ఖండన బిందువులు
A(2, 2\(\sqrt{2}\)), B(2, -2\(\sqrt{2}\))
కావలసిన వైశాల్యం X- అక్షం దృష్ట్యా సౌష్ఠవము
OACB వైశాల్యము

ప్రశ్న 3.
y = 2 – x², y = x² వక్రాల మధ్య వైశాల్యం ఎంత ?
సాధన:

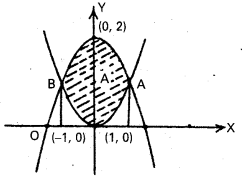
y = 2 – x² —- (1)
y = x² —- (2)
x² = -(y – 2)
(2) నుండి
2 – x² = x²
2 = 2x² లేదా x² = 1
x = ±1
రెండు వక్రాల మధ్య వైశాల్యము

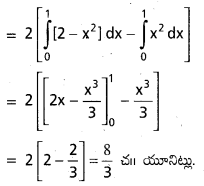
ప్రశ్న 4.
y² = 12(x + 3), y² = 20 (5 – x) వక్రాల మధ్య ఆవృతమైన వైశాల్యం 64\(\sqrt{\frac{5}{3}}\) అని చూపండి.
సాధన:
వక్రాల సమీకరణాలు
y² = 12 (x + 3) —- (1)
y² = 20(5 – x) —- (2)
y ను తొలగించగా
12(x + 3) = 20(5 – x)
3x + 9 = 25 – 5x
8x = 16
x = 2
y² = 12(2 + 3) = 60
y = \(\sqrt{60}\) = ±2\(\sqrt{15}\)

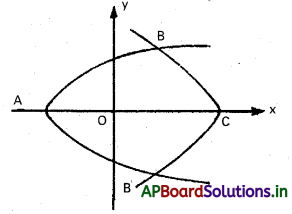
ఖండన బిందువులు (2, 2\(\sqrt{15}\)) B’ (+2, -2\(\sqrt{15}\))
కావలసిన వైశాల్యము X – అక్షం దృష్ట్యా సౌష్ఠవము.
వైశాల్యము ABCB’

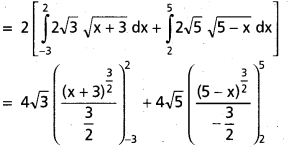
ప్రశ్న 5.
{(x, y), x² – x – 1 ≤ y ≤ -1} ప్రదేశం వైశాల్య౦ కనుక్కోండి.
సాధన:

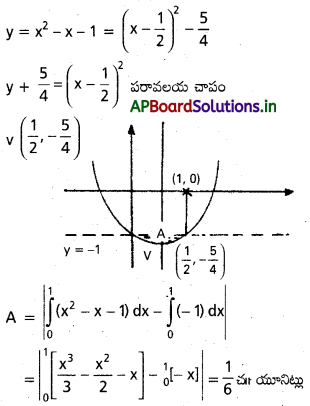
ప్రశ్న 6.
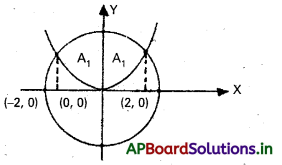
x² + y² = 8 వృత్తం 2y = x² పరావలయంతో రెండు భాగాలుగా విభజించబడింది. ఈ రెండు భాగాల వైశాల్యాలు కనుక్కోండి.
సాధన:
వక్ర సమీకరణాలు
x² + y² = 8 —- (1)
2y = x² —– (2)
(1), (2) ల మధ్య y ని తొలగించగా

x² = t
4t + t² = 32
t² + 4t – 32 = 0
(t + 8) (t − 4) = 0
t = -8 (అసాధ్య౦) x² = 4 ⇒ x = ±2

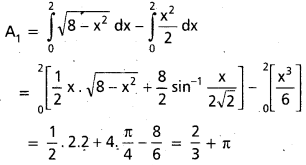
వక్రం Y- అక్షం దృష్ట్యా సౌష్ఠవము
మొత్తము వైశాల్యము
A = 2A₁ = 2(\(\frac{2}{3}\) + π) = \(\frac{4}{3}\) + 2π చ|| యూనిట్లు.
మిగిలిన వైశాల్యం = 8π – (\(\frac{4}{3}\) + 2π)
= (6π – \(\frac{4}{3}\)) చ|| యూనిట్లు.

ప్రశ్న 7.
\(\frac{x^2}{a^2}\) + \(\frac{\mathbf{y}^2}{\mathbf{b}^2}\) = 1 (దీర్ఘవృత్తం) తో పరిబద్ధమైన ప్రదేశం
వైశాల్యం π ab అని చూపండి. దీని నుంచి x² + y² = a² వృత్తం వైశాల్యం రాబట్టండి. (May ’05)
సాధన:

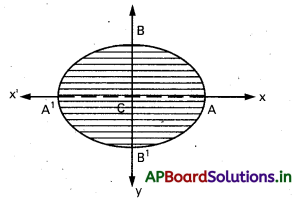
x మరియు y అక్షాల యొక్క దీర్ఘవృత్త వైశాల్యము
= 4 వైశాల్య౦ CAB
= 4 . \(\frac{\pi}{4} a b\)
దీర్ఘవృత్త వైశాల్యము \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
y = \(\frac{b}{a} \sqrt{a^2-x^2}\)
CAB = \(\frac{b}{a} \int_0^a \sqrt{a^2-x^2} d x\)

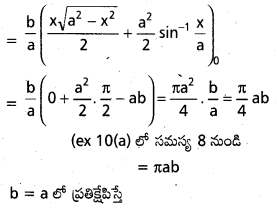
x² + y² = a² వృత్త వైశాల్యము వస్తుంది.
వృత్త వైశాల్యము = πа(a) = πа² చ|| యూనిట్లు.

ప్రశ్న 8.
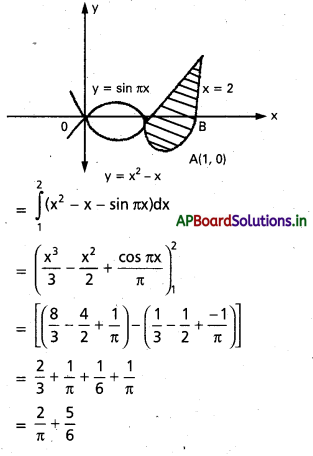
y sin πx, y = x² – x, x = 2 వక్రాలతో అన్నతమైన ప్రదేశం వైశాల్యం కనుకోండి.
సాధన:
కావలసిన వైశాల్యము

ప్రశ్న 9.
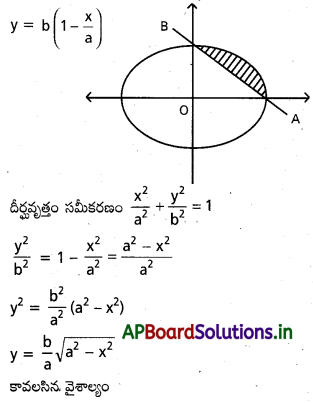
OA = 3, OB = b అయినప్పుడు \(\frac{x^2}{a^2}\) + \(\frac{y^2}{b^2}\) = 1 దీర్ఘవృత్తం ధన పాదం AOB అనుకుందాం. అప్పుడు దీర్ఘవృత్తం జ్యా AB కి, చాపం A, B కి మధ్య పరి బద్ధమైన వైశాల్యం \(\frac{(\pi-2) a b}{4}\) అని చూపండి.
సాధన:
OA = a, OB = b అనుకొనుము
AP సమీకరణము \(\frac{x}{a}\) + \(\frac{y}{b}\) = 1
\(\frac{y}{b}\) = 1 – \(\frac{x}{a}\)

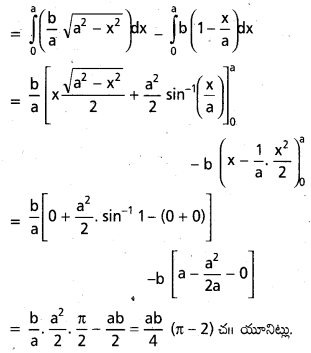
ప్రశ్న 10.
x = 0, x = 4, y = 4, y = 0 రేఖలతో పరిబద్ధమైన చతురస్ర వైశాల్యాన్ని వక్రాలు y² = 4x, x² = 4y మూడు సమాన భాగాలుగా విభజిస్తాయని చూపండి.
సాధన:

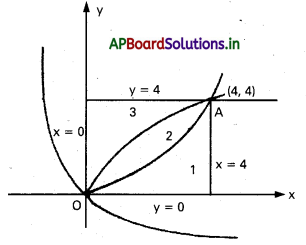
దత్త సమీకరణాలు y² = 4x —– (1)
x² = 4y —– (2)
ఖండన బిందువులు O(0, 0), A(4, 4)

(1) వైశాల్యం = (2) వైశాల్యం = (3) వైశాల్యం

Students can go through AP Inter 2nd Year Physics Notes 6th Lesson ప్రవాహ విద్యుత్తు will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 6th Lesson ప్రవాహ విద్యుత్తు

→ వాహకం ఏదైనా భాగం గుండా పోవు ఆవేశ ప్రవాహపు రేటును విద్యుత్ ప్రవాహసత్వం అంటారు.
i.e., i = Q. దీనిని ఆంపియర్లలో కొలుస్తారు.

→ ఓమ్ నియమము : స్థిర ఉష్ణోగ్రత వద్ద, వాహకం గుండా పోవు విద్యుత్ ప్రవాహం, దాని పొటెన్షియల్ తేడాకు అనులోమానుపాతంలో ఉండును. V & I లేక V = IR. ఇక్కడ ‘R’ వాహకము లేక నిరోధకము యొక్క

→ నిరోధకము, విద్యుత్ ప్రవాహంను వ్యతిరేకించు ఒక సాధనము.

→ అధిక పొటెన్షియల్ నుండి అల్ప పొటెన్షియల్కు మరియు ఎలక్ట్రాన్ ప్రవాహ దిశకు వ్యతిరేకంగా సాంప్రదాయక విద్యుత్ ప్రవాహం దిశ ఉండును.

→ ఓమ్ నియమమును పాటించు నిరోధకములను ఓమిక్ నిరోధకములు అంటారు.

→ ఓమ్ నియమమును పాటించని నిరోధకములను అఓమిక్ నిరోధకములు అంటారు.

→ ప్రమాణ పొడవు మరియు ప్రమాణ మధ్యచ్ఛేద వైశాల్యం ఉన్న ఒక తీగ నిరోధంను నిరోధకత లేక విశిష్ట నిరోధం అంటారు.
i.e., ρ = \(\frac{\mathrm{RA}}{l}\) దీని ప్రమాణము Ω – m.

→ ప్రమాణ మధ్యచ్ఛేద వైశాల్యం ఉన్న విద్యుత్ ప్రవాహంను విద్యుత్ ప్రవాహ సాంద్రత (J) అంటారు. దీని ప్రమాణం A/m².

→ నిరోధం యొక్క విలోమమును కండక్టెన్స్ అంటారు. దీనికి ప్రమాణం సీమెన్.

→ నిరోధకత యొక్క విలోమమును వాహకత్వం అంటారు.
i.e., σ = \(\frac{1}{\rho}\) దీని ప్రమాణం సీమెన్ / మీటర్.

→ 1°C ఉష్ణోగ్రత పెరుగుదలలో నిరోధం పెరుగుదలకు మరియు 0°C వద్ద నిరోధంనకు గల నిష్పత్తిని ఉష్ణోగ్రత నిరోధ గుణకం (α) అంటారు.

→ ఏకాంక ఉష్ణోగ్రత పెరుగుదలకు నిరోధకతలో కలిగే అంశిక పెరుగుదలను ఉష్ణోగ్రతా నిరోధకత గుణకం (α) అంటారు.
i.e., α = \(\frac{\rho_{\mathrm{t}}-\rho_0}{\rho_0 \mathrm{t}}\)

→ ప్రమాణ ఆవేశంను కదిలించుటలో జరిగిన పనిని ఘటం విద్యుచ్ఛాలక బలం (వి.చా.బ) అంటారు.
E = \(\frac{W}{q}\)మరియు ఓల్టలో కొలుస్తారు.

→ ఘటం విద్యుత్ విశ్లేష్యం గుండా ప్రవహించు ఆవేశాలను వ్యతిరేకించు నిరోధంను అంతర నిరోధం అంటారు.

→ వలయంలో ఆవేశ ప్రభాహంలను ఘటంలో ఏర్పడే వి. చా.బ వ్యతిరేకించును. దీనిని తిరో వి.చా.బ అంటారు.

→ లోహ వాహకంపై బాష విద్యుత్ క్షేత్రంను ప్రయోగిస్తే ఎలక్ట్రాన్ వడితో అపసరం చెందును. దీనినే అపసర వేగం లేక డ్రిఫ్ట్ వేగం అంటారు.

→ ప్రమాణ విద్యుత్ క్షేత్రసత్వంను అనువర్తింపచేస్తే, ఫలిత సరాసరి అపసర వేగంను మొబిలిటి (μ) అంటారు. μ = \(\). దీని ప్రమాణము m²s^-1 Volt^-1.

→ ద్రవాలలో విద్యుత్ ప్రవాహంను ఎలక్ట్రాలిసిస్ అంటారు. ఇది అయాన్ల చలనం వల్ల ఉండును.

→ వాయువులలో విద్యుత్ ప్రవాహంను ఉత్సర్గం (డిశ్చార్జ్) అంటారు. ఇది అయాన్ల చలనం వల్ల ఉండును.

→ E. వి.చా.బ. జనకంను బాహ్య నిరోధం R కు కలిపితే, వోల్టేజి V_{బాహ్య}, R వెంట V_{బాహ్య} = I(R + r). ఇక్కడ r జనకం అంతర నిరోధం.

→ నిరోధకంల శ్రేణి సంధానంలో, మొత్తం నిరోధం R_s = R₁ + R₂ + ……….. + R_n

→ నిరోధకంల సమాంతర సంధానంలో, మొత్తం నిరోధం \(\frac{1}{R_P}=\frac{1}{R_1}+\frac{1}{R_2}+\ldots \ldots \cdot \frac{1}{R_n}\)

→ కిర్కాఫ్ సంధి నియమం : వలయం ఏదైనా సంధి వద్ద, సంధి వద్దకు వచ్చు విద్యుత్ ప్రవాహాల బీజీయ మొత్తం, సంధి నుండి బయటకు వచ్చు విద్యుత్ ప్రవాహాల బీజీయ మొత్తమునకు సమానం.

→ కిర్కాఫ్ లూప్ నియమం: ఏదైనా సంవృత లూప్లో పొటెన్షియల్ తేడాల బీజీయ మొత్తం శూన్యం.

→ వీటన్ బ్రిడ్జి సూత్రము R₄ = R₃ × \(\frac{\mathrm{R}_2}{\mathrm{R}_1}\)

→ మీటర్ బ్రిడ్జి, వీటన్ బ్రిడ్జి సూత్రంపై ఆధారపడును.

→ మీటర్ బ్రిడ్జిని ఉపయోగించి తెలియని నిరోధంను ఖచ్చితంగా కొలవవచ్చును.

→ పొటెన్షియోమీటర్ చాలా సున్నితమైంది, ఖచ్చితమైన పొటెన్షియల్ తేడాను కనుగొనుటకు ఉపయోగిస్తారు.

→ విద్యుత్ ప్రవాహం I = \(\frac{\mathrm{q}}{\mathrm{t}}=\frac{\mathrm{ne}}{\mathrm{t}}\)

→ అపసర్గ వేగం, V_d = \(\frac{\mathrm{eE} \tau}{\mathrm{m}}\)

→ I = neA V_d; I = \(\frac{\mathrm{nAe}^2 \tau}{\mathrm{m}}\)E

→ ఎలక్ట్రాన్ చలనశీలత, m = \(\frac{\mathrm{e} \tau}{\mathrm{m}}\)

→ ప్రవాహ సాంద్రత j = \(\frac{\mathrm{I}}{\mathrm{A}}\) మరియు j = \(\frac{\mathrm{ne}^2 \tau}{\mathrm{m}}\)E

→ ఓమ్స్ నియమము, V = IR

→ నిరోధం, R = \(\frac{V}{I}\) మరియు R = \(\frac{\rho l}{\mathrm{~A}}\); R = \(\frac{\mathrm{m}}{\mathrm{ne}^2 \tau} \cdot \frac{l}{\mathrm{~A}}\); ρ = \(\frac{\mathrm{m}}{\mathrm{ne}^2 \tau}\)

→ కండక్టేన్స్ G = \(\frac{1}{R}\); వాహకత్వం σ = \(\frac{1}{ρ}\)

→ ఉష్ణోగ్రత నిరోధ గుణకం α = \(\frac{\mathrm{R}-\mathrm{R}_0}{\mathrm{R}_0 \theta}\)

→ కార్బన్ నిరోధం కలర్ కోడ్

→ శ్రేణి సంధానంలో R_s = R₁ + R₂ + R₃ + …………

→ సమాంతర సంధానంలో, \(\frac{1}{\mathrm{R}_{\mathrm{p}}}=\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\frac{1}{\mathrm{R}_3}\) + …………..

→ టెర్మినల్ పొటెన్షియల్ తేడా లేక టెర్మినల్ వోల్టేజి V = E – Ir = \(\left[\frac{E-V}{V}\right]\)R

→ కిర్కాఫ్ మొదటి నియమము నుండి Σi = 0

→ కిర్కాఫ్ రెండవ నియమము నుండి ΣE = ΣIR

→ వీటన్ బ్రిడ్జి సూత్రము, R₄ = R₃ × \(\frac{\mathrm{R}_2}{\mathrm{R}_1}\)

Students can go through AP Inter 2nd Year Physics Notes 5th Lesson స్థిర విద్యుత్ పోటెన్షియల్ – కెపాసిటెన్స్ will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 5th Lesson స్థిర విద్యుత్ పోటెన్షియల్ – కెపాసిటెన్స్

→ ప్రమాణ ధనావేశంను అనంత దూరం నుండి క్షేత్ర దిశకు వ్యతిరేకంగా ఒక బిందువు వద్దకు తీసుకురావటానికి ‘ చేయవలసిన పనిని విద్యుత్ పొటెన్షియల్ అంటారు.

→ ప్రమాణ ధనావేశంను విద్యుత్ క్షేత్రదిశకు వ్యతిరేకంగా ఒక బిందువు నుండి మరొక బిందువుకు జరుపుటకు చేయవలసిన పనిని ఆ క్షేత్రంలో ఆ రెండు బిందువుల మధ్య పొటెన్షియల్ తేడా అంటారు.

→ బిందు ఆవేశం వల్ల విద్యుత్ పొటెన్షియల్ V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\)

→ q₁ మరియు q₂, ఆవేశాల స్థిరవిద్యుత్ స్థితిజశక్తి = U(q₁, q₂) = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r}\)

→ q₁, q₂, మరియు q₃, ఆవేశాల వ్యవస్థ స్థిరవిద్యుత్ స్థితిజశక్తి = U(q₁, q₂, q₃) = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1 q_2}{r_1}+\frac{q_2 q_3}{r_2}+\frac{q_3 q_1}{r_3}\right]\)

→ విద్యుత్ ద్విధ్రువం పొటెన్షియల్ V = \(\frac{P \cos \theta}{4 \pi \varepsilon_0 r^2}\)

→ తలంపై అన్ని బిందువుల వద్ద పొటెన్షియల్ విలువ స్థిరంగా ఉంటే, ఆ తలంను సమశక్మతలం (సమపొటెన్షియల్) అంటారు.

→ విద్యుత్ క్షేత్రం మరియు పొటెన్షియల్ల మధ్య సంబంధం E = \(-\frac{\delta \mathrm{V}}{\delta l}=+\frac{|\delta \mathrm{V}|}{\delta l}\)

→ బాహ్యక్షేత్రంలో ఒక (డైపోల్) ద్విధ్రువం స్థితిజశక్తి U(θ) = PE(cos θ₀ – cos θ₁)

→ ప్రమాణ ఘనపరిమాణంలో ద్విధ్రువ భ్రామకంను, ధ్రువణం (polarisation) అంటారు. దీనిని P తో సూచిస్తారు.

→ కెపాసిటర్ అల్ప పొటెన్షియల్ వద్ద అధిక ఆవేశంను నిల్వచేయు సాధనం C = \(\frac{\mathrm{Q}}{\mathrm{V}}\)

→ సమాంతర పలకల కెపాసిటర్ కెపాసిటి, C = \(\frac{\varepsilon_0 A}{d}\)

→ శ్రేణి సంధానంలో, \(\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}+\ldots \ldots\)

→ సమాంతర సంధానంలో, C = C₁ + C₂ + C₃ + ……….

→ C కెపాసిటేన్స్, Q ఆవేశం మరియు V ఓల్టేజి ఉన్న కెపాసిటర్ లో నిల్వ ఉండు శక్తి, U = \(\frac{1}{2}\)CV² = \(\frac{\mathrm{Q}^2}{2 \mathrm{C}}=\frac{\mathrm{QV}}{2}\)

→ ఒక రోథకంను బాహ్యక్షేత్రం (E) ఉంచితే ధ్రువణం చెందును. ధ్రువణం వల్ల రోధకంలో E దిశకు వ్యతిరేకంగా Eo ప్రేరణ విద్యుత్ క్షేత్రం ఏర్పడును. రోథకంలోపల నికర విద్యుత్ క్షేత్రం E = E₀ – E_i = \(\frac{\mathrm{E}_0}{\mathrm{~K}}\)

→ వాక్ డీ గ్రాఫ్ జనరేటర్ అధిక వోల్టేజ్లను (కొన్ని మిలియన్. వోల్ట్స్) ఉత్పత్తి చేయు ఒక యంత్రము ఫలిత విద్యుత్ క్షేత్రాలను ఉపయోగించి హెచ్చు శక్తులకు (ఎలక్ట్రాన్స్, ప్రోటాన్స్, అయాన్లు) ఆవేశ కణాలను త్వరణం చెందించును.

→ విద్యుత్ క్షేత్ర రేఖీయ సమాకలనమును

→ రెండు బిందువులు A మరియు B ల మధ్య పొటెన్షియల్ తేడా
V_B – V_A = \(-\int_A^B \vec{E} \cdot \mathrm{d} \overrightarrow{\mathrm{i}}\); V_B – V_A = \(\frac{\mathrm{q}}{4 \pi \varepsilon_0}\left[\frac{1}{\mathrm{r}_{\mathrm{B}}}-\frac{1}{\mathrm{r}_{\mathrm{A}}}\right]\)

→ బిందు ఆవేశం q వల్ల విద్యుత్ పొటెన్షియల్, V = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\)

→ ఆవేశాల వ్యవస్థ వల్ల విద్యుత్ పొటెన్షియల్, V = \(\frac{1}{4 \pi \varepsilon_0} \sum_{i=1}^n \frac{q_i}{r_i}\)

→ విద్యుత్ ద్విధ్రువం వల్ల ఏదైనా బిందువు వద్ద విద్యుత్ పొటెన్షియల్ V = \(\frac{1}{4 \pi \varepsilon_0} \frac{P \cos \theta}{\left(r^2-a^2 \cos ^2 \theta\right)}\)

→ E = \(\frac{-\mathrm{dv}}{\mathrm{dr}}\)

→ గాలిలో C = \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\) యానకంలో C = \(\frac{\mathrm{K}_0 \mathrm{~A}}{\mathrm{~d}}\)

→ సమాంతర పలకల కెపాసిటర్ రెండు పలకల మధ్య ఖాళీలో రోధక దిమ్మెను పాక్షికంగా నింపబడితే, కెపాసిటి
C = \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\)

→ గోళాకార కెపాసిటర్ కెపాసిటి C = 4πε₀\(\frac{a b}{b-a}\)

→ స్థూపాకార కెపాసిటర్ C = \(\frac{2 \pi \varepsilon_0 l}{\log _{\mathrm{e}}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)}\)

→ ఆవేశాల పంపిణీలో కెపాసిటర్లను కలిపితే, ఉమ్మడి పొటెన్షియల్ V = \(\frac{\mathrm{C}_1 \mathrm{~V}_1+\mathrm{C}_2 \mathrm{~V}_2+\mathrm{C}_3 \mathrm{~V}_3+\ldots \ldots}{\mathrm{C}_1+\mathrm{C}_2+\mathrm{C}_3+\ldots \ldots}\)