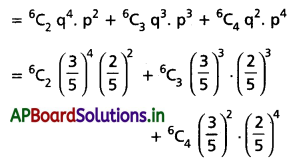Inter 2nd Year

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 10 యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు to solve questions creatively.

AP Intermediate 2nd Year Maths 2A యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు Formulas

→ యాదృచ్ఛిక చలరాశి : ఒక యాదృచ్ఛిక ప్రయోగం శాంపిల్ ఆవరణం S అనుకుందాం. ఏదైనా ప్రమేయం X : S → R ను యాదృచ్ఛిక చలరాశి అంటాం.

→ సంభావ్యతా విభాజన ప్రమేయం : X ఒక యాదృచ్ఛిక చలరాశి అప్పుడు F : R → R ప్రతి X ∈ Rకు F(x) = P(X ≤ x) తో నిర్వచితమైన ప్రమేయాన్ని X కు సంభావ్యతా విభాజన ప్రమేయం అంటాం.

→ X : S → R ఒక యాదృచ్ఛిక చలరాశి. X వ్యాప్తి పరిమితం లేదా అపరిమిత గణ్యసమితి అయితే X ను విచ్ఛిన్న చలరాశి అని, అట్లా కాకపోతే అవిచ్ఛిన్న యాదృచ్ఛిక చలరాశి అని అంటాం.

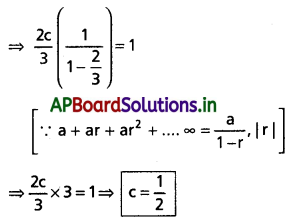
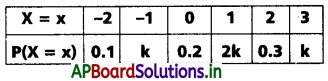
→ X : S → R ఒక విచ్ఛిన్న యాదృచ్ఛిక చలరాశి. దాని వ్యాప్తి = {X₁, X₂, ….} అయిన \(\sum_{r=1}^n P\left(X_r\right)\) = 1, P(X_r) ≥ 0.

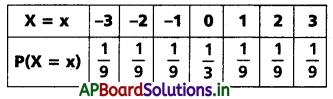
→ X ఒక విచ్ఛిన్న యాదృచ్ఛిక చలరాశి. దాని వ్యాప్తి {X₁, X₂, ……} అనుకుందాం. ప్రతి n కు P(X = x_n) తెలిసి, Σx_n P(X = x_n) అనే మొత్తం పరిమితమైతే, ఆ మొత్తాన్ని X కు మధ్యమం (లేదా సగటు) అంటాం. దీన్ని µ తో సూచిస్తాం. (i.e.,) µ = Σx_n P(X = x_n)
Σ(x_n – µ)² P(X = x_n) అనేది ఒక పరిమిత సంఖ్య అయితే ఆ మొత్తాన్ని X కు విస్తృతి అంటాం.

→ X విస్తృతిని σ² తో సూచిస్తే, σ ను X కు క్రమ విచలనం అంటారు.
∴ μ = Σx_n P(X = x_n); σ² = Σ(x_n – μ)² P(X = x_n) = \(\Sigma x_n^2 P\left(X=x_n\right)\) – μ²

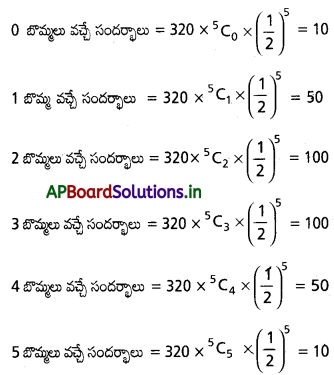
→ ద్విపద విభాజనం: n ఒక ధన పూర్ణాంకం. p వాస్తవ సంఖ్య మరియు 0 ≤ p ≤ 1. యాదృచ్ఛిక చలరాశి వ్యాప్తి {0, 1, 2, 3, …. n}. X ద్విపద చలరాశి లేదా ద్విపద విభాజనాన్ని పాటిస్తూ, n, p లు పరామితులుగా గల్గి వుంటే, P(X = r) = ⁿC_r . p^r q^n-r; r = 0, 1, 2, ….. n మరియు q = 1 – p అవుతుంది.

→ ద్విపద విభాజనాన్ని X ~ B(n, p) గా లేదా P(X = r) = ⁿC_r p^r q^n-r . p^r, r = 0, 1, 2, 3, …. n లేదా (q + p)ⁿతో సూచిస్తాం.

→ ద్విపద విభాజనం యొక్క మధ్యమం = np. ద్విపద విభాజనం యొక్క విస్తృతి = npq, క్రమవిచలనం = \(\sqrt{n p q}\).

→ పాయిజాన్ విభాజనం : λ > 0 ఒక స్థిరరాశి. యాదృచ్ఛిక చలరాశి X యొక్క వ్యాప్తి {0, 1, 2, ….}
P(X = k) = \(\frac{\lambda^k}{k !} e^{-\lambda}\), (k = 0, 1, 2, …….) అనుకుంటే, λ పరామితిగా, X పాయిజాన్ విభాజనాన్ని అనుసరిస్తుందని అంటాం. X ను పాయిజాన్ యాదృచ్ఛిక చలరాశి అంటాం. పాయిజాన్ విభాజనానికి మధ్యమము = λ, విస్తృతి = λ, క్రమ విచలనం = √λ

→ ఈ క్రింది షరతులకు లోబడి పాయిజాన్ విభాజనాన్ని, ద్విపద విభాజనపు సమతాస్థితి (limiting case) గా ఉజ్జాయింపు చేయవచ్చు.

• యత్నాల సంఖ్య n అనిశ్చితమైనంత పెద్దది, అంటే n → ∞
• ప్రతి యత్నంలో గెలుపు సంభావ్యత (స్థిరం) అతిస్వల్పం, అంటే p → 0

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 9 సంభావ్యత to solve questions creatively.

AP Intermediate 2nd Year Maths 2A సంభావ్యత Formulas

→ యాదృచ్ఛిక ప్రయోగం : ఒక ప్రయోగంలో ఏ ఫలితం వస్తుందో ముందే చెప్పలేనిదై, ఆ ప్రయోగ ఫలితాల జాబితా ముందే తెలిసి ఉండి, ఒకే విధమైన పరిస్థితుల్లో ఆ ప్రయోగాన్ని ఎన్నిసార్లైనా చేయడానికి వీలుంటే ఆ ప్రయోగాన్ని యాదృచ్ఛిక ప్రయోగం అంటాం.

→ లఘుఘటన, ఘటన ఒక యాదృచ్ఛిక ప్రయోగంలోని ఫలితాన్ని లఘుఘటన అంటాం. కొన్ని లఘు ఘటనల సమూహాన్ని ఘటన అంటాం.

→ పరస్పర వివర్జిత ఘటనలు: రెండు లేదా అంతకంటే ఎక్కువ ఘటనల్లో ఏదైనా ఒక ఘటన సంభవించడం, మిగతా ఘటనల సంభవాన్ని నిరోధించేటట్టుంటే, అటువంటి ఘటనలను పరస్పర వివర్జిత ఘటనలు అంటారు.

→ సమ సంభవ ఘటనలు: రెండు లేదా అంతకంటే ఎక్కువ ఘటనల్లో ఏ ఘటన అయినా మిగతా ఘటనల కంటే ఎక్కువగా సంభవిస్తుందనడానికి కారణమేమి లేకపోతే, అటువంటి ఘటనలను సమసంభవ ఘటనలు అంటారు.

→ పూర్ణ ఘటనలు : ఒక యాదృచ్ఛిక ప్రయోగంలోని రెండు లేదా అంతకంటే ఎక్కువ ఘటనల్లో ఆ ప్రయోగం ఫలితం వాటిలో ఒక్కదానికైనా చెందేటట్లుంటే, అటువంటి ఘటనలను పూర్ణ ఘటనలు అంటాం.

→ సంభావ్యత సాంప్రదాయిక (లేదా గణితాత్మక) నిర్వచనం : ఒక యాదృచ్ఛిక ప్రయోగంలో n పూర్ణ, పరస్పర వివర్జిత, సమసంభవ ఘటనలుండి వాటిలో ఏదైనా ఘటన E జరగడానికి m అనుకూల ఫలితాలుంటే, ఆ ఘటన సంభావ్యతను P(E) తో సూచిస్తూ, P(E) = \(\frac{m}{n}\) గా నిర్వచిస్తాం. 0 ≤ P(E) ≤ 1

→ శాంపిల్ ఆవరణ : ఒక యాదృచ్ఛిక ప్రయోగపు ఫలితాన్ని లఘుఘటన అంటాం. ఒక యాదృచ్ఛిక ప్రయోగంలోని ఫలితాలన్నింటితో కూడిన సమితిని ఆ యాదృచ్ఛిక ప్రయోగానికి సంబంధించి శాంపిల్ ఆవరణ అంటాం. దీనిని S తో సూచిస్తాం. S లోని మూలకాలను శాంపిల్ బిందువులు అంటాం. S లో ప్రతిమూలకం, యాదృచ్ఛిక ప్రయోగం యొక్క ఒక ఫలితం S. ఒక ఉపసమితిని ఘటన అంటాం. అంటే, ఒక లఘుఘటనల సమితినే ఘటన అంటాం.

→ S శాంపిల్ ఆవరణ E ⊂ S.E లో ఒకే ఒక మూలకం ఉంటే E ని లఘుఘటన అంటాం. ఒక ప్రయోగ ఫలితం ఘటన E సంభవించింది లేదా జరిగింది అంటాం. అలాకాకపోతే ఘటన E సంభవించలేదు అంటాం.

→ Φ, S లు S కి ఉపసమితులు. వాటిని వరసగా అసంభవ ఘటన, నిశ్చిత ఘటన అంటాం.

→ ఘటన E కి పూరక ఘటనను E^C తో సూచిస్తాం. E^C = S – E శాంపిల్ ఆవరణ S కు E₁, E₂ లు రెండు ఘటనలు. అంటే E₁ ⊆ S, E₂ ⊆ S మరియు E₁ ∩ E₂ = Φ అయితే E₁, E₂ లను పరస్పర వివర్జిత ఘటనలు అంటాం.

→ ఘటనలు E₁, E₂, ……., E_n లు i ≠ j లకు 1 ≤ i, j ≤ n లకు E_i ∩ E_j = Φ అయ్యేటట్లుంటే, వాటిని పరస్పర వివర్జిత ఘటనలు అంటాం.

→ ఘటనలు E₁, E₂, …… E_k లు E₁ ∪ E₂ ∪ E₃ ∪ E_k = S అయితే వాటిని పూర్ణ ఘటనలు అంటాం. శాంపిల్ ఆవరణ S లో E₁, E₂లు రెండు ఘటనలు పూరక ఘటనలైన E₁ ∪ E₂ = S, E₁ ∩ E₂ = Φ.

→ ఒక యాదృచ్ఛిక ప్రయోగంకి శాంపిల్ ఆవరణ S. ఈ ప్రయోగపు అన్ని ఘటనల సమితి P(S) తో సూచిస్తాం. ఇచ్చట P(S), Sకు ఘాత సమితి.

→ సంభావ్యతా స్వీకృత నిర్వచనం: ఒక యాదృచ్ఛిక ప్రయోగపు శాంపిల్ ఆవరణ S. ప్రమేయం P : P(S) → R

→ క్రింది స్వీకృతాలను ధ్రువపరిస్తే Pని సంభావ్యతా ప్రమేయం అంటాం.

• P(E) ≥ 0 ∀ E ∈ P(S) (ధన స్వీకృతం)
• P(S) = 1 (పూరణ స్వీకృతం)
• E₁, E₂ ∈ P(S), E₁ ∩ E₂ = Φ అయితే P(E₁ ∪ E₂) = P(E₁) + P(E₂) (సమ్మేళును స్వీకృతం)
• ప్రతి E ∈ P(S) కు P(E) ను ఘటన E సంభావ్యత అంటాం.

→ శాంపిల్ ఆవరణ Sలో E ఒక ఘటన అయితే 0 ≤ P(E) ≤ 1. శాంపిల్ ఆవరణ Sలో E ఒక ఘటన అయితే

• P(E) : P(\(\bar{S}\)) ను E కు అనుకూలత అని
• P(E) : P(E) ను E కు ప్రతికూలత అంటాం.

→ సంభావ్యతపై సంకలన సిద్ధాంతం: ఒక యాదృచ్ఛిక ప్రయోగంలో E₁, E₂ లు రెండు ఘటనలైతే P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)

→ శాంపిల్ ఆవరణ Sకు E₁, E₂ లు రెండు ఘటనలు.
P(E₂ – E₁) = P(E₂) – P(E₁ ∩ E₂) మరియు P(E₁ – E₂) = P(E₁) – P(E₁ ∩ E₂)

→ E₁, E₂, E₃ లు శాంపిల్ ఆవరణ Sలో మూడు ఘటనలు అయిన P(E₁ ∪ E₂ ∪ E₃) = P(E₁) + P(E₂) + P(E₃) – P(E₁ ∩ E₂) – P(E₂ ∩ E₃) – P(E₃ ∩ E₁) + P(E₁ ∩ E₂ ∩ E₃)

→ ఒక యాదృచ్ఛిక ప్రయోగపు ఘటనలు A, Bలు అనుకుందాం. అప్పుడు “A జరిగిన తరువాత B జరగడం” అనే ఘటనను నియత ఘటన అంటాం. దీనిని \(\frac{B}{A}\) తో సూచిస్తాం. ఇట్లే \(\frac{A}{B}\) అనే ఘటన “B జరిగిన తరువాత A జరగడం” అనే ఘటనను సూచిస్తుంది.

→ నియత సంభావ్యత : ఘటన A జరిగిందని ఇస్తే, ఘటన B జరిగే సంభావ్యతను P(B/A) తో సూచిస్తాం. P(B/A) ని నియత సంఖ్య అంటాం.
దీనిని P(B/A) = \(\frac{P(B \cap A)}{P(A)}\), P(A) > 0 గా నిర్వచిస్తాం. ఇట్లే P(A/B) = \(\frac{P(B \cap A)}{P(B)}\), P(B) > 0.
సూచన : P(A/B) = \(\frac{n(A \cap B)}{n(B)}\); P(B/A) = \(\frac{n(B \cap A)}{n(A)}\)

→ నియత సంభావ్యతకు గణన సిద్ధాంతం ఒక శాంపిల్ ఆవరణం S లోని ఘటనలు A, Bలు ; P(A) > 0, P(B) > 0, అయితే P(A ∩ B) = P(A) . P(B/A) = P(B) . P(A/B).

→ స్వతంత్ర ఘటనలు : రెండు ఘటనలు A, Bలు P(A ∩ B) = P(A) . P(B) అయితే వాటిని స్వతంత్ర ఘటనలు అంటాం. అలాకాకపోతే A, B లను అస్వతంత్ర ఘటనలు అంటాం.

→ బేయీ సిద్ధాంతం: ఒక ప్రయోగంలో E₁, E₂, ……., E_n లు పరస్పర వివర్జిత, పూర్ణ ఘటనలవుతూ, P(E_i) > 0, i = 1, 2, …. n అయినప్పుడు k = 1, 2, 3, ….. n లకు
\(P\left(\frac{E_k}{A}\right)=\frac{P\left(E_k\right) \cdot P\left(\frac{A}{E_k}\right)}{\sum_{i=1}^n P\left(E_i\right) \cdot P\left(\frac{A}{E_i}\right)}\)

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 8 విస్తరణ కొలతలు to solve questions creatively.

AP Intermediate 2nd Year Maths 2A విస్తరణ కొలతలు Formulas

→ అవర్గీకృత దత్తాంశానికి మధ్యమం = \(\frac{విచలనాల మొత్తం}{పరిశీలనల సంఖ్య}\) = \(\frac{\Sigma x_i}{n}\)

→ అవర్గీకృత దత్తాంశానికి మధ్యగతం: ముందుగా దత్త n పరిశీలనలను పరిమాణపరంగా అవరోహణ లేదా ఆరోహణ క్రమంలో వ్రాయవలెను.

→ n బేసి సంఖ్య అయితే \(\frac{n+1}{2}\) వ పరిశీలనల అవర్గీకృత దత్తాంశం యొక్క మధ్యగతం అగును.

→ n సరి సంఖ్య అయితే \(\frac{n}{2}\) మరియు \(\frac{n+2}{2}\) వ పరిశీలనల సరాసరిను అవర్గీకృత దత్తాంశం యొక్క మధ్యగతం అగును.

→ వర్గీకృత మరియు అవర్గీకృత దత్తాంశానికి వ్యాప్తి, మధ్యమ విచలనం, విస్తృతి మరియు ప్రామాణిక విచలనం కొన్ని విస్తరణ కొలతలు

→ వ్యాప్తిని దత్తాంశ గరిష్ట విలువకు, కనిష్ఠ విలువకు మధ్యగల భేదంగా నిర్వచిస్తారు.

→ అవర్గీకృత విభాజనానికి మధ్యమ విచలనం

• మధ్యమం నుంచి మధ్యమ విచలనం = \(\frac{\sum\left|x_i-\bar{x}\right|}{n}, \bar{x}\) మధ్యమం
• మధ్యగతం నుంచి మధ్యమ విచలనం = \(\frac{\sum \mid x_i-\text { మధ్యగతం } \mid}{n}\)

→ వర్గీకృత దత్తాంశానికి మధ్యమ విచలనం

• మధ్యమం నుంచి మధ్యమ విచలనం = \(\frac{1}{N} \sum f_i\left|x-\bar{x}_i\right|\); N = Σf_i, మరియు \(\bar{x}\) మధ్యమం
• మధ్యగతం నుంచి మధ్యమ విచలనం = \(\frac{1}{N} \sum f_i \mid x_i\) – మధ్యగతం|, N = Σf_i

→ అవర్గీకృత దత్తాంశానికి విస్తృతి, σ² = \(\frac{1}{n}\) = \(\sum\left(x_i-\bar{x}\right)^2\), ప్రామాణిక విచలనం σ = \(\sqrt{\frac{1}{n} \sum\left(x_1-\bar{x}\right)^2}\)

→ విచ్ఛిన్న పౌనఃపున్య విభాజనానికి విస్తృతి, σ² = \(\frac{1}{N}\) = \(\sum f_i\left(x_i-\bar{x}\right)^2\), \(\bar{x}\) మధ్యమం

→ ప్రామాణిక విచలనం σ = \(\sqrt{\frac{1}{N} \sum f_i\left(x_i-\bar{x}\right)^2}\)

→ అవిచ్ఛిన్న పౌనఃపున్య విభాజనానికి ప్రామాణిక విచలనం σ = \(\frac{1}{N} \sqrt{N \sum f_i x_i^2-\left(\sum f_i x_i\right)^2}\) (లేదా) σ = \(\frac{h}{N} \sqrt{N \Sigma f_i y_i^2-\left(\Sigma f_i y_i\right)^2}, y_i=\frac{x_i-A}{h}\)

→ విచలనాంకం = \(\frac{\sigma}{x} \times 100(\bar{x} \neq 0)\)

→ దత్తాంశంలోని ప్రతి పరిశీలనను ఒక స్థిరరాశి K చే గుణించినపుడు ఫలితంగా వచ్చే పరిశీలనల విస్తృతి, తొలిపరిశీలనల విస్తృతికి K² రెట్లు ఉంటుంది.

→ పరిశీలనలు x₁, x₂, …….., x_n లలో ప్రతిదానిని K కి పెంచితే లేదా కలిపితే (K ఒక ధనాత్మక లేదా ఋణాత్మక సంఖ్య), వచ్చే పరిశీలనల విస్తృతి మారదు.

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 7 పాక్షిక భిన్నాలు to solve questions creatively.

AP Intermediate 2nd Year Maths 2A పాక్షిక భిన్నాలు Formulas

→ f(x), Φ(x) లు రెండు బహుపదులు. Φ(x) ఒక శూన్యేతర బహుపది (i.e.,) Φ(x) ≠ 0 అయితే \(\frac{f(x)}{\phi(x)}\) ను అకరణీయ భిన్నం అంటాం.

→ f(x) తరగతి Φ(x) తరగతి కంటే తక్కువ అయితే \(\frac{f(x)}{\phi(x)}\) ను క్రమభిన్నమని అంటారు.

→ f(x) తరగతి ≥ Φ(x) తరగతి అయిన \(\frac{f(x)}{\phi(x)}\) ను అపక్రమ భిన్నమని అంటారు.

→ \(\frac{f(x)}{\phi(x)}\) క్రమభిన్నం

→ Φ(x) కు పునరావృతం కాని ఏకఘాత కారణాంకాలున్నప్పుడు Φ(x) లో (ax + b) రూపంలో ఉండే ప్రతి కారణాంకానికి సంబంధించి \(\frac{A}{a x+b}\) అనే పాక్షిక భిన్నం ఉంటుంది A వాస్తవ సంఖ్య.

→ Φ(x) కు పునరావృతం అయ్యేవి, కానివి ఏకఘాత కారణాంకాలున్నప్పుడు, Φ(x) కు (ax + b)ⁿ, n ∈ N రూపంలో వుండే ప్రతి పునరావృత కారణాంకానికి సంబంధించి \(\frac{A_1}{a x+b}+\frac{A_2}{(a x+b)^2}\) + …… + \(\frac{A_n}{(a x+b)^n}\) అనే n పాక్షిక భిన్నాలుంటాయి. ఇక్కడ A₁, A₂, ……., A_n లు వాస్తవ స్థిరాంకాలు.

→ Φ(x) కు ax² + bx + c రూపంలో పునరావృతం కాని అవిభాజ్య కారణాంకం ఉన్నప్పుడు Φ(x) కు ax² + bx + c రూపంలో ఉన్న ప్రతి కారణాంకానికి సంబంధించి \(\frac{A x+B}{a x^2+b x+c}\); A, B లు వాస్తవ స్థిరరాసులు, రూపంలో ఒక పాక్షిక భిన్నం ఉంటుంది.

→ Φ(x) కు ax² + bx + c రూపంలో పునరావృతం కాని అవిభాజ్య కారణాంకం ఉన్నప్పుడు Φ(x) కు (ax² + bx + c)ⁿ రూపంలో ఉన్న ప్రతి కారణాంకానికి సంబంధించి n పాక్షిక భిన్నాలు \(\frac{A_1 x+B_1}{a x^2+b x+c}+\frac{A_2 x+B_2}{\left(a x^2+b x+c\right)^2}+\ldots . .+\frac{A_n x+B_n}{\left(a x^2+b x+c\right)^n}\), n ధన పూర్ణాంకం, A₁, A₂, ……, A_n, B₁, B₂, ………, B_n లు స్థిరరాసుల రూపంలో వుంటాయి.

→ Φ(x) కు ax² + bx + c రూపంలో పునరావృతం అయ్యేవి. కానివి అవిభాజ్య కారణాంకాలున్నప్పుడు, థ(x) కు (ax² + bx + c)ⁿ రూపంలో ఉన్న ప్రతి కారణాంకానికి సంబంధించి n పాక్షిక భిన్నాలు.

→ \(\frac{f(x)}{\phi(x)}\) అపక్రమ భిన్నమైతే \(\frac{f(x)}{\phi(x)}=q(x)+\frac{R(x)}{\phi(x)}\) అని వ్రాయవచ్చు. ఇచ్చట q(x) అనేది f(x) ను Φ(x) చే భాగించగా వచ్చే భాగఫలం, R(x) శేషం, R(x) తరగతి Φ(x), తరగతి కన్నా తక్కువ \(\frac{R(x)}{\phi(x)}\) ను పాక్షిక భిన్నాల మొత్తంగా వ్రాయటానికి పై పద్ధతులను ఉపయోగిస్తారు.

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 6 ద్విపద సిద్ధాంతం to solve questions creatively.

AP Intermediate 2nd Year Maths 2A ద్విపద సిద్ధాంతం Formulas

→ n ఒక ధన పూర్ణాంకం, x, a లు వాస్తవ సంఖ్యలు అయితే
(x + a)ⁿ = ⁿC₀ . xⁿ . a⁰ + ⁿC₁ . x^n-1 . a¹ + ⁿC₂ . x^n-2 . aⁿ + …… + ⁿC_r . x^n-r a^r +……. + ⁿC_n . x⁰ . aⁿ = \(\sum_{r=0}^n{ }^n C_r \cdot x^{n-r} \cdot a^r\)

→ (x + a)ⁿ విస్తరణలో (n + 1) పదాలున్నాయి.

→ (x + a)ⁿ విస్తరణలోని rవ పదాన్ని T_r తో సూచిస్తే T_r = ⁿC_(r-1) x^n-r+1 a^r-1, 1 ≤ r ≤ n+1

→ (x + a)ⁿ విస్తరణలో (r + 1)వ పదాన్ని ‘సాధారణ పదం’ (General Term) అంటాం.
i.e., T_r+1 = ⁿC_r . x^n-r. a^r ; r = 0, 1, 2, ….., n.

→ (a + b + c)ⁿ విస్తరణలో పదాల సంఖ్య = \(\frac{(n+1)(n+2)}{2}\)

→ n సరిసంఖ్య (ధన పూర్ణాంకం) అయితే (x + a)ⁿ విస్తరణలో మధ్య పదం = \(T_{\left(\frac{n}{2}+1\right)}\)

→ n బేసిసంఖ్య (ధన పూర్ణాంకం) అయితే (x + a)ⁿ విస్తరణలో రెండు మధ్య పదాలుంటాయి. అవి \(T_{\left(\frac{n+1}{2}\right)}\), \(T_{\left(\frac{n+3}{2}\right)}\)

→ \(\frac{(n+1)|x|}{|x|+1}\) = p, ధన పూర్ణాంకమైన, (1 + x)ⁿ విస్తరణలో pవ, (p + 1)వ పదాలు సంఖ్యాత్మకంగా గరిష్ఠ పదాలు అవుతాయి. మరియు |T_p| = |T_p+1|

→ \(\frac{(n+1)|x|}{|x|+1}\) = p + F; p ధన పూర్ణాంకం, 0 < F < 1 అయిన (1 + x)ⁿ విస్తరణలో (p + 1)వ పదం సంఖ్యాత్మకంగా గరిష్ఠ పదం అవుతుంది.

→ C₀, C₁, C₂, …….., C_n లు ద్విపద గుణకాలు అంటాం. ఇచ్చట C_r = ⁿC_r, r = 0, 1, 2, ….. n

• C₀ + C₁ + C₂ + …… + C_n = \(\sum_{r=0}^n c_r\) = 2ⁿ
• C₀ – C₁ + C₂ – C₃ + ……. (-1)ⁿ C_n = 0
• C₀ + C₂ + C₄ + …… = C₁ + C₃ + C₅ + …….. = 2^n-1
• \(\sum_{r=0}^n r \cdot{ }^n C_r\) = n . 2^n-1
• \(\sum_{r=2}^n(r)(r-1) \cdot{ }^n C_r\) = (n) (n – 1) . 2^n-2
• \(\sum_{r=1}^n r^2 \cdot{ }^n C_r\) = (n) (n + 1) . 2^n-2
• a . C₀ + (a + d) . C₁ + (a + 2d) . C₂ + ……. + (a + nd) . C_n = (2a + nd) 2^n-1
• C₀C_r + C₁C_r+1 + C₂C_r+2 + C_n-rC_n = ⁽²ⁿ⁾C_(n-r) = ⁽²ⁿ⁾C_(n+r) = \(\frac{(2 n) !}{(n+r) !(n-r) !}\)

→ f(x) = a₀ + a₁x + a₂x² + ….. + a_nxⁿ అయిన

• గుణకాల మొత్తం = f(1)
• x యొక్క సరి ఘాతాల గుణకాల మొత్తం = \(\frac{f(1)+f(-1)}{2}\)
• x యొక్క బేసి ఘాతాల గుణకాల మొత్తం = \(\frac{f(1)-f(-1)}{2}\)

→ m అకరణీయ సంఖ్య, x ఒక వాస్తవ సంఖ్య, |x| < 1 అయితే
(1 + x)^m = \(1+\frac{m}{1} x+\frac{(m)(m-1)}{1.2} x^2+\frac{(m)(m-1) \ldots .(m-r+1)}{1.2 .3 \ldots . .(r)} \cdot x^r+\ldots \ldots\)
= \(1+\sum_{r=1}^{\infty} \frac{(m n)(m-1) \ldots .(m-r+1)}{1.2 \cdot 3 \ldots . . r^{\prime}} x^r\)

→ (1 – x)^-n = \(1+n x+\frac{(n)(n+1)}{1.2} x^2+\ldots+\frac{(n)(n+1) \ldots(n+r-1)}{1: 2.3 \ldots \ldots(r)} x^r+\ldots\)

→ |x| < 1, p, q ∈ N అయిన
\((1-x)^{-p / q}=1+\frac{p}{1}\left(\frac{x}{q}\right)+\frac{(p)(p+q)}{1.2}\left(\frac{x}{q}\right)^2+\ldots .+\frac{(p)(p+q) \ldots .[p+(r-1) q]}{1.2 .3 \ldots . . r}\left(\frac{x}{q}\right)^r+\ldots .\)

→ \((1+x)^{-p / q}=1-p\left(\frac{x}{q}\right)+\frac{(p)(p+q)}{1.2}\left(\frac{x}{q}\right)^2+\ldots \ldots\) \(+(-1)^r \frac{(p)(p+q) \ldots(p+(\overline{r-1}) q)}{1.2 \cdot 3.4 \ldots .(r)} \cdot\left(\frac{x}{q}\right)^r+\ldots .\)

→ \((1+x)^{p / q}=1+\frac{p}{1 !}\left(\frac{x}{q}\right)+\frac{(p)(p-q)}{1.2}\left(\frac{x}{q}\right)^2+\ldots\) \(+\frac{(p)(p-q)(p-2 q) \ldots \ldots(p-(\overline{r-1}) q)}{r !}\left(\frac{x}{q}\right)^r+\ldots .\)

→ \((1-x)^{p / q}\) లో Tr+1 = \((-1)^r \frac{(p)(p-q)(p-2 q) \ldots \ldots(p-(\overline{r-p}) q)}{r !}\left(\frac{x}{q}\right)^r\)

→ n ధన పూర్ణాంకం, x ఒక వాస్తవ సంఖ్య ; |x| < 1 అయితే

• (1 + x)^-n = \(1-\frac{n}{1 !} x+\frac{(n)(n+1)}{2 !} x^2+\ldots . .+\ldots .+(-1)^r \frac{(n)(n+1) \ldots .(n+r-1)}{r !} x^r\) \(+\ldots \infty=\sum_{r=0}^{\infty}(-1)^{r(n+r-1)} C_r \cdot x^r\)
• (1 – x)^-n = \(1+\frac{n}{1 !} x+\frac{(n)(n+1)}{2 !} x^2+\ldots .+\ldots .+\frac{(n)(n+1)(n+2) \ldots \ldots(n+r-1)}{r !} x^r\) \(+\ldots \infty=\sum_{r=0}^{\infty}{ }^{(n+r-1)} C_r \cdot x^r\)

→ x², ఆపై x ఘాతాలు ఉపేక్షించేంతగా, |x| చిన్నదయితే (1 + x)ⁿ = 1 + nx

→ x³, ఆపై x ఘాతాలు ఉపేక్షించేంతగా, |x| చిన్నదయితే, (1 + x)ⁿ = 1 + nx + \(\frac{(n)(n-1)}{1.2} x^2\)

→ x⁴, ఆపై x ఘాతాలు ఉపేక్షించేంతగా, |x| చిన్నదయితే, (1 + x)ⁿ = 1 + nx + \(\frac{(n)(n-1)}{2 !} x^2+\frac{(n)(n-1)(n-2)}{3 !} x^3\)

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 5 ప్రస్తారాలు-సంయోగాలు to solve questions creatively.

AP Intermediate 2nd Year Maths 2A ప్రస్తారాలు-సంయోగాలు Formulas

→ ప్రాథమిక సూత్రం: ఒక పని W₁ ను ‘m’ విభిన్న విధాలుగానూ, మరొక పని W₂ ను ‘n’ విభిన్న విధాలుగానూ చేయగలిగితే, ఈ రెండు పనులునూ ఒకేసారి ‘mn’ విభిన్న విధాలుగా చేయవచ్చు.

→ n అనేది ఋణేతర పూర్ణాంకం అయిన (i) 0! = 1 (ii) n! = n(n – 1)!

→ ఇచ్చిన వస్తువుల నుంచి (ఒకే విధంగా లేక విభిన్లు) కొన్ని లేదా అన్నీ ఎంచుకొని ఒక వరసలో (సరళరేఖలో) అమర్చడాన్ని ఒక ‘రేఖీయ ప్రస్తారం’ లేదా ‘ప్రస్తారం’ అంటాం.

→ n, r లు ధన పూర్ణాంకాలు, r ≤ n అయినప్పుడు ‘n’ విభిన్న వస్తువుల నుంచి ఒక్కొక్కసారి ‘r’ వస్తువుల చొప్పున తీసుకొంటే వచ్చే ప్రస్తారాల సంఖ్యను ⁿP_r తో సూచిస్తాం.
ⁿP_r = \(\frac{n !}{(n-r) !}\), 0 ≤ r ≤ n

→ n, r లు ధన పూర్ణాంకాలు, r ≤ n అయిన

• ⁿP_r = n . ^(n-1)P_(r-1), r ≥ 1
• ⁿP_r = (n) . (n – 1) ^(n-2)P_(r-1), r ≥ 2
• ⁿP_r = ^(n-1)P_r + r . ^(n-1)P_(r-1)

→ n అసరూప వస్తువుల నుంచి ‘r’ వస్తువుల చొప్పున తీసుకొంటే వచ్చే ప్రసారాలలో

• నిర్దేశించిన ఒక వస్తువు ఉండే ప్రస్తారాల సంఖ్య (r) ^(n-1)P_(r-1)
• నిర్దేశించిన ఒక వస్తువు లేని ప్రస్తారాల సంఖ్య ^(n-1)P_r
• నిర్దేశించిన ఒక వస్తువు నిర్ధేశించిన స్థానంలో ఉండే ప్రస్తారాల సంఖ్య = ^(n-1)P_(r-1)

→ A లో వున్న విభిన్న మూలకాల సంఖ్య n(A); B లో వున్న విభిన్న మూలకాల సంఖ్య n(B) అయితే n(A) ≤ n(B) అయినపుడు A నుండి B కు గల విభిన్న అన్వేక ప్రమేయాల సంఖ్య ^n(B)P_n(A)

→ n(A) = n(B) అయినపుడు A నుండి B కు గల ద్విగుణప్రమేయాల సంఖ్య n(A)!

→ A నుండి B కు గల ప్రమేయాల సంఖ్య [n(B)]^n(A)

→ పునరావృతాన్ని అనుమతించినపుడు n విభిన్న వస్తువులతో, r వస్తువులుండేటట్లు ఏర్పరచగల ప్రస్తారాల సంఖ్య n^r.

→ n విభిన్న శూన్యేతర 1, 2, 3, ……, 9 అంకెలను ఉపయోగించి పునరావృతం లేకుండా ఏర్పరచగల r స్థానాలు గల సంఖ్యల మొత్తం ^(n-1)P_(r-1) × (దత్త అంకెల మొత్తం) × (111…. r సార్లు).

→ పైన చెప్పిన అంశంలోని n విభిన్న పూర్ణాంకాలలో ‘0’ కూడా ఉన్నప్పుడు ఏర్పరచగల 7 స్థానాలున్న సంఖ్యల మొత్తం = ^(n-1)P_(r-1) × దత్త అంకెల మొత్తం × (111……. r సార్లు) ^(n-2)P_(r-2) × (దత్త అంకెలమొత్తం × (111 – (r – 1) సార్లు)

→ n విభిన్న వస్తువుల నుంచి వచ్చే వృత్తాకార ప్రస్తారాల సంఖ్య = (n – 1)!

→ n విభిన్న వస్తువులతో ఏర్పడే పువ్వుల దండలు, పూసల గొలుసులు వంటి వేలాడే రకం వృత్తాకార ప్రస్తారాల సంఖ్య \(\frac{1}{2}\) (n – 1)!

→ ఇచ్చిన n వస్తువులలో p వస్తువులు ఒక రకంగానూ, q వస్తువులు మరొక రకంగానూ, r వస్తువులు వేరొక రకంగానూ ఉంటూ మిగిలిన వస్తువులు విభిన్నంగా ఉంటే, ఈ n వస్తువులను అమర్చడం ద్వారా వచ్చే ప్రస్తారాల సంఖ్య \(\frac{n !}{p ! q ! r !}\)

→ n విభిన్న వస్తువుల నుండి ‘r’ వస్తువుల వంతున తీసుకొంటే వచ్చే సంయోగాల సంఖ్యను ⁿC_r తో సూచిస్తాం. మరియు ⁿC_r = \(\frac{n !}{(n-r) ! r !}\), 0 ≤ r ≤ n

→ n, r లు ధన పూర్ణాంకాలు, 0 ≤ r ≤ n అయితే ⁿC_r = ⁿC_(n-r)

→ n, r, s ధన పూర్ణాంకాలు 0 ≤ r ≤ n, 0 ≤ s ≤ n మరియు ⁿC_r = ⁿC_s అయితే r = s లేదా r + s = n అవుతుంది.

→ (m ≠ n) అయినపుడు (m + n) విభిన్న వస్తువుల నుండి m, n వస్తువులు ఉన్న రెండు భాగాలుగా విభజించే విధానాల సంఖ్య ^{(m + n)}C_m = ^{(m + n)}C_n = \(\frac{(m+n) !}{m ! n !}\)

→ ఇట్లే m, n, p లు విభిన్న ధన పూర్ణాంకాలయినప్పుడు (m + n + p) వస్తువులను m, n, p వస్తువులున్న 3 భాగాలుగా విభజించే విధానాల సంఖ్య \(\frac{(m+n+p) !}{m ! n ! p !}\)

→ ‘mn’ విభిన్న వస్తువులను ‘m’ సమభాగాలుగా (ఒక్కొక్క భాగంలో n వస్తువులుండే విధంగా) విభజించే విధాల సంఖ్య \(\frac{(m n) !}{(n !)^m m !}\)

→ (mn) విభిన్న వస్తువులను m వ్యక్తులకు సమానంగా పంచే విధాల సంఖ్య \(\frac{(m n) !}{(n !)^n}\)

→ ఒక రకం సరూప వస్తువులు p, మరొక రకం సరూప వస్తువులు q, వేరొక రకం సరూప వస్తువులు r ఇచ్చినపుడు వాటి నుంచి ఒకటి లేదా అంత కంటే ఎక్కువ వస్తువులను ఎంచుకొనే విధానాల సంఖ్య (p + 1) (q + 1) (r + 1) – 1.

→ m ధన పూర్ణాంకాం మరియు \(p_1^{\alpha_i} \cdot p_2^{\alpha_2} \ldots \ldots p_k^{\alpha_k}\) అవుతూ, p₁, p₂, ……., p_k లు విభిన్న ప్రధాన సంఖ్యలు α₁, α₂, ….., α_k ధన పూర్ణాంకాలు అయినపుడు m కు గల ధన భాజకాల సంఖ్య (α₁ + 1) (α₂ + 1) …… (α_k + 1), (1, m లతో కలిపి)

→ n విభిన్న వస్తువుల నుండి 0, 1, 2,…… లేదా n వస్తువులతో ఏర్పడే సంయోగాల సంఖ్య ⁿC₀ + ⁿC₁ + ⁿC₂ + …… + ⁿC_r = 2ⁿ

→ n విభిన్న వస్తువుల నుండి ఒకటి లేదా అంతకంటే ఎక్కువ వస్తువులతో ఏర్పడే సంయోగాల సంఖ్య = 2ⁿ – 1

→ n భుజాలున్న బహుభుజిలో కర్ణాల సంఖ్య = \(\frac{n(n-3)}{2}\)

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 4 సమీకరణ వాదం to solve questions creatively.

AP Intermediate 2nd Year Maths 2A సమీకరణ వాదం Formulas

→ n రుణేతర పూర్ణసంఖ్య; a₀, a₁, a₂, ……, a_n లు వాస్తవ లేదా సంకీర్ణ సంఖ్యలు, a_n ≠ 0 అయితే, అప్పుడు f(x) = a₀ xⁿ + a₁ x^n-1 + a₂ x^n-2 + ….. + a_n సమాసాన్ని x లో nవ తరగతి బహుపది అంటాం.

→ f(x) = a₀ xⁿ + a₁ x^n-1 + a₂ x^n-2 + ….. + a_n = 0 సమీకరణాన్ని nవ తరగతి బీజీయ సమీకరణం లేదా బహుపది సమీకరణం అంటాం. ఇచ్చట a₀ ≠ 0

→ f(α) = 0 అయితే, సంకీర్ణ సంఖ్య α ను బహుపది f(x) = 0 సమీకరణానికి మూలం అని అంటాం.

→ f(α) = 0 అయిన f(x) సమాసానికి (x – α) ఒక కారణాంకం అవుతుంది.

→ సమీకరణ మూలాలు, గుణకాల మధ్య సంబంధం:
(i) x³ + p₁x² + p₂x + p₃ = 0 సమీకరణ మూలాలు α₁, α₂, α₃, అయితే, అప్పుడు

• s₁ = α₁ + α₂ + α₃ = -p₁
• s₂ = α₁α₂ + α₂α₃ + α₃α₁ = p₂
• s₃ = α₁α₂α₃ = -p₃

(ii) x⁴ + p₁x³ + p₂x² + p₃x + p₄ = 0 సమీకరణ మూలాలు α₁, α₂, α₃, α₄ అయిన, అప్పుడు

• s₁ = α₁ + α₂ + α₃ + α₄ = -p₁
• s₂ = α₁α₂ + α₂α₃ + α₃α₄ + α₁α₃ + α₁α₄ + α₂α₄ = p₂
• s₃ = α₁α₂α₃ + α₂α₃α₄ + α₃α₄α₁ + α₁α₂α₄ = -p₃
• s₄ = α₁α₂α₃α₄ = p₄

→ ఒక ఘన సమీకరణ మూలాలు

• అంకశ్రేఢిలో ఉంటే వాటిని a – d, a, a + d గా తీసుకొంటాం.
• గుణశ్రేఢిలో ఉంటే \(\frac{a}{r}\), a, ar గా తీసుకుంటాం.
• హరాత్మక శ్రేఢిలో ఉంటే వాటిని \(\frac{1}{a-d}, \frac{1}{a}, \frac{1}{a+d}\) గా తీసుకొంటాం.

→ ఒక ద్వివర్గ సమీకరణ మూలాలు

• అంకశ్రేఢిలో ఉంటే వాటిని a – 3d, a – d, a + d, a + 3d గా తీసుకొంటాం.
• గుణశ్రేఢిలో ఉంటే వాటిని \(\frac{a}{r^3}, \frac{a}{r}\), ar, ar³ గా తీసుకొంటాం.
• హరాత్మక శ్రేఢిలో ఉంటే వాటిని \(\frac{1}{a-3 d}, \frac{1}{a-d}, \frac{1}{a+d}, \frac{1}{a+3 d}\) గా తీసుకొంటాం.

→ వాస్తవ సంఖ్యలు గుణకాలుగా గల బహుపదీయ సమీకరణానికి సంకీర్ణ మూలాలు సంయుగ్మంగా ఉంటాయి.

→ అకరణీయ సంఖ్యలు గుణకాలుగా గల బహుపదీయ సమీకరణానికి కరణీయ మూలాలు సంయుగ్మాలు.
ఉదా: 2 + √3 ఒక మూలమైతే, 2 – √3 కూడా మూలం అవుతుంది.

→ α₁, α₂, ….., α_n లు f(x) = 0 కు మూలాలైన,

• -α₁, -α₂, ……, -α_n లు మూలాలుగా గల బహుపది సమీకరణం f(-x) = 0 అవుతుంది.
• kα₁, kα₂, ….. kα_n లు మూలాలుగా గల సమీకరణం f(\(\frac{x}{k}\)) = 0, (k ≠ 0)
• \(\frac{1}{\alpha_1}, \frac{1}{\alpha_2}, \ldots \frac{1}{\alpha_n}\) లు మూలాలుగా గల సమీకరణం f(\(\frac{1}{x}\)) = 0
• α₁ + h, α₂ + h, ……., α_n + h లు మూలాలుగా గల సమీకరణం f(x – h) = 0
• α₁ – h, α₂ – h, ……, α_n – h లు మూలాలుగా గల సమీకరణం f(x + h) = 0
• \(\alpha_1^2, \alpha_2^2, \ldots \alpha_n^2\) లు మూలాలుగా గల సమీకరణం f(√x) = 0

→ f(x) = p₀ xⁿ + p₁ x^n-1 + p₂ x^n-2 + …… + p_n = 0 సమీకరణంలో రెండవ పదం తొలగింపు చేయటానికి f(x) = 0 ను f(x + h) = 0 గా రూపాంతరం చెందించాలి. ఇచ్చట h = \(\frac{-p_1}{\text { (n) } p_0}\) అవుతుంది.

→ f(x) = 0 బహుపది సమీకరణంలో x బదులు \(\frac{1}{x}\) ప్రతిక్షేపించినా, ఆ సమీకరణంలో మార్పు లేనట్లయితే f(x) = 0 ను వ్యుత్కృమ సమీకరణం (Reciprocal equation) అంటారు.

→ f(x) = 0 వ్యుత్కృమ సమీకరణంలోని గుణకాలన్నీ p_i = p_n-i (i = 0, 1, 2, …., n) పాటిస్తే మొదటి కోవకు (Class one) చెందిన వ్యుత్త మ సమీకరణమనీ; p_i = -p_n-i; పాటిస్తే రెండో కోవకు (Class two) చెందిన వృత్తమ సమీకరణమనీ అంటాం.

→ మొదటి కోవకు చెందిన బేసి వ్యుత్ప్రమ సమీకరణానికి -1 ఒక మూలం అవుతుంది. ఈ సందర్భంలో రెండో కోవకు చెందిన వ్యుతమ సమీకరణానికి 1 మూలం అవుతుంది.

→ రెండో కోవకు చెందిన సరిపరిమాణ వ్యుతమ సమీకరణానికి 1, -1 లు మూలాలు అవుతాయి.

→ f(x) = 0 సమీకరణం n వ తరగతికి చెందినదై, దానిలో ‘r’ వ పదాన్ని తొలగించటానికి దానిని f(x + h) = 0 కు రూపాంతరం చెందించిన, (h స్థిరాంకం) f^(n-r+1) (h) = 0 కావలయును (i.e.,.) f(x) యొక్క (n – r + 1) వ అవకలనం x = h వద్ద సున్నా కావలయును.

→ f(x) = 0 మూలాన్ని కనుక్కోవటానికి f(x) = 0 ని తృప్తిపరిచే x విలువను కనుక్కోవాలి. కొన్ని సందర్భాలలో పరిశీలన ద్వారా ఈ పని చేయవచ్చు. ఈ పద్ధతిని యత్న-దోష పద్ధతి అంటాం.

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 3 వర్గసమాసాలు to solve questions creatively.

AP Intermediate 2nd Year Maths 2A వర్గసమాసాలు Formulas

→ a, b, c లు వాస్తవ సంఖ్యలు లేదా సంకీర్ణ సంఖ్యలు అయి, a ≠ 0 అయినపుడు ax² + bx + c రూపంలోని బహుపదిని, చలరాశి x లో వర్గ సమాసం అంటాం.
ఉదా: 4x² – 2x + 3

→ aα² + bα + c = 0 అయితే, సంకీర్ణ సంఖ్య ‘α’ ను ax² + bx + c వర్గ సమాసానికి సున్న అంటాం.

→ a, b, c లు వాస్తవ సంఖ్యలు లేదా సంకీర్ణ సంఖ్యలు అయి, a ≠ 0 అయినపుడు ax² + bx + c = 0 రూపంలో ఉన్న సమీకరణాన్ని చలరాశి x లో వర్గ సమీకరణం అంటాం. a, b, c లను ఈ సమీకరణ గుణకాలు అంటాం.
ఉదా: 2x² – 5x + 6 = 0

→ aα² + bα + c = 0 అయితే, సంకీర్ణ సంఖ్య α ను ax² + bx + c = 0 సమీకరణానికి మూలం అనిగానీ, సాధన అనిగానీ అంటాం.

→ ax² + bx + c = 0 వర్గ సమీకరణం మూలాలు \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)

→ α, β లు ax² + bx + c = 0 లు వర్గ సమీకరణ మూలాలు అయితే α + β = \(\frac{-b}{a}\); αβ = \(\frac{c}{a}\)

→ α, β లు మూలాలు గల వర్గ సమీకరణం x² – (α + β)x + αβ = 0

→ వర్గ సమీకరణం మూలాల స్వభావం: ∆ = b² – 4ac ని వర్గ సమాసం ax² + bx + c, వర్గ సమీకరణం ax² + bx + c = 0 ల “విచక్షణి” అంటాం.

→ α, β లు వర్గ సమీకరణం ax² + bx + c = 0 కి మూలాలు అనుకోండి.
సందర్భం 1: a, b, c లు వాస్తవ సంఖ్యలు అయితే అప్పుడు

• ∆ = 0 ⇔ α = β = \(\frac{-b}{2 a}\) (ax² + bx + c = 0) కు ద్విరుక్త మూలం
• ∆ > 0 ⇔ α, β లు విభిన్న వాస్తవ సంఖ్యలు.
• ∆ < 0 ⇔ α, β లు వాస్తవేతర పరస్పర సంయుగ్మ సంకీర్ణ సంఖ్యలు.

సందర్భం 2: a, b, c లు అకరణీయ సంఖ్యలు అయితే అప్పుడు

• ∆ = 0 ⇔ α, β లు సరిసమానమైన అకరణీయ సంఖ్యలు (= \(\frac{-b}{2 a}\), ద్విరుక్త మూలం).
• ∆ > 0 శూన్యేతర అకరణీయ సంఖ్య యొక్క వర్గం ⇔ α, β లు అకరణీయ సంఖ్యలు.
• ∆ ధనాత్మకం, కానీ అకరణీయ సంఖ్య యొక్క వర్గం కాదు ⇔ α, β లు సంయుగ్మ కరణులు.
• ∆ < 0 ⇔ α, β లు వాస్తవేతర పరస్పర సంయుగ్మ సంకీర్ణ సంఖ్యలు.

→ \(a_1 x^2+b_1 x+c_1=0, a_2 x^2+b_2 x+c_2=0\) వర్గ సమీకరణాల మూలాలు, ఏకీభవించడానికి ఆవశ్యక, పర్యాప్త నియమం \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

→ \(a_1 x^2+b_1 x+c_1=0, a_2 x^2+b_2 x+c_2=0\) వర్గ సమీకరణాలకు ఉమ్మడి మూలం ఉండటానికి ఆవశ్యక, పర్యాప్త నియమం (c₁a₂ – c₂a₁)² = (a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁) మరియు ఉమ్మడి మూలం = \(\frac{c_1 a_2-c_2 a_1}{a_1 b_2-a_2 b_1}\)

→ f(x) = ax² + bx + c = 0 వర్గ సమీకరణంకు మూలాలు α, β లు అనుకుందాం.

• c ≠ 0 అయితే, అప్పుడు αβ ≠ 0, \(\frac{1}{\alpha}, \frac{1}{\beta}\) లు మూలాలుగా గల సమీకరణం f(\(\frac{1}{x}\)) = 0;
• α + k, β + k లు మూలాలుగా గల సమీకరణం f(x – k) = 0.
• α – k, β – k లు మూలాలుగా గల సమీకరణం f(x + k) = 0.
• -α, -β లు మూలాలు గల సమీకరణం f(-x) = 0.
• kα, kβ లు మూలాలు గల సమీకరణం f(\(\frac{x}{k}\)) = 0

→ a, b, c ∈ R, a ≠ 0 అనుకొందాం. అప్పుడు R లోని అన్ని x లకు ax² + bx + c = 0, ‘a’ లకు ఒకే గుర్తు ఉంటేనే ax² + bx + c = 0 మూలాలు వాస్తవేతర సంకీర్ణ సంఖ్యలవుతాయి.

→ α, β లు ax² + bx + c = 0 వర్గ సమీకరణం మూలాలై, α < β అయితే, అప్పుడు

• α < x < β అయినప్పుడు, ax² + bx + c, ‘a’ లకు వ్యతిరేక గుర్తులు ఉంటాయి.
• x < α లేదా x > β అయినప్పుడు, ax² + bx + c, ‘a’ లకు ఒకే గుర్తులు ఉంటాయి.

→ a < 0 అయితే, ax² + bx + c వర్గ సమాసానికి, x = \(\frac{-b}{2a}\) వద్ద పరమ గరిష్ఠ విలువ ఉంటుంది.
గరిష్ట విలువ = \(\frac{4 a c-b^2}{4 a}\)

→ a > 0 అయితే, ax² + bx + c వర్గ సమాసానికి x = \(\frac{-b}{2a}\) వద్ద పరమ కనిష్ఠ విలువ ఉంటుంది.
కనిష్ట విలువ = \(\frac{4 a c-b^2}{4 a}\)

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 2 డిమోయర్ సిద్ధాంతం to solve questions creatively.

AP Intermediate 2nd Year Maths 2A డిమోయర్ సిద్ధాంతం Formulas

→ ‘n’ పూర్ణాంకము అయితే, (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ

→ n అకరణీయ సంఖ్య అయితే, (cis θ)ⁿ కు ఒక విలువ cis(nθ)

→ 1 యొక్క n -వ మూలాలు: cis(\(\frac{2 k \pi}{n}\)), k = 0, 1, 2, 3, … (n – 1)

→ 1 యొక్క ఘనమూలాలు: ఏకకపు ఘనమూలాలు 1, ω, ω²

• ω³ = 1
• 1 + ω + ω² = 0
• ω = \(\frac{-1+i \sqrt{3}}{2}\), ω² = \(\frac{-1-i \sqrt{3}}{2}\)
• 1, ω, ω² లు గుణశ్రేఢిలో ఉన్నవి.

→ z₀ = r₀ cis θ₀ ≠ 0 అయితే Z₀ యొక్క n-వ మూలాలు \(\alpha_k=r_0^{1 / n} {cis}\left(\frac{2 k \pi+\theta_0}{n}\right)\), k = 0, 1, 2,… (n – 1).

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 1 సంకీర్ణ సంఖ్యలు to solve questions creatively.

AP Intermediate 2nd Year Maths 2A సంకీర్ణ సంఖ్యలు Formulas

→ సంకీర్ణ సంఖ్య నిర్వచనం: x, y ∈ R కు z = x + iy రూపంలో \(\sqrt{-1}\) అనగా i² = -1 రూపంలో సంఖ్యలను సంకీర్ణ సంఖ్యలు అందురు. ఇందులో x ను z యొక్క వాస్తవ భాగమని మరియు y ను z కు కల్పిత భాగమని అందురు. వీటిని Re(z), Im(z) తో సూచిస్తాం.
x = 0 మరియు y ≠ 0 ⇔ Re(z) = 0 మరియు Im(z) ≠ 0 అయిన Z = x + iy ను శుద్ధ కల్పిత సంఖ్య (i.e) y ≠ 0 ⇔ Im(z) ≠ 0 అయిన z= x + iy వాస్తవము కాని సంఖ్య అగును.

→ వాస్తవసంఖ్యల క్రమయుగ్మాన్ని సంకీర్ణ సంఖ్య అంటాం. సంకీర్ణ సంఖ్యా సమితిని C తో సూచిస్తాం. అంటే C = {(a, b)/ a ∈ R, b ∈ R} = R × R

→ a = c, b = d అయితే రెండు సంకీర్ణ సంఖ్యలు z₁ = (a, b), z₂ = (c, d) లకు సమానం అంటాం.

→ z₁ = (a, b), z₂ = (c, d) అయితే

• z₁ + z₂ = (a + c, b + d)
• z₁, z₂ = (a – c, b – d)
• z₁z₂ = (ac – bd, ad + bc)
• \(\frac{z_1}{z_2}=\left(\frac{a c+b d}{c^2+d^2}, \frac{b c-a d}{c^2+d^2}\right)\)

→ మాపము – ఆయామం: సంకీర్ణ సంఖ్య z = x + iy ను P(x, y) బిందువు రూపంలో XOY-తలంలో సూచించిన ఆ తలమును ఆర్లాండ్ తలము అందురు.
|OP| పొడవును z యొక్క మాపము అని, దీనిని |z| చే సూచించెదరు మరియు ∠XOP = θ ను z కు ఆయామం లేదా Arg Z తో సూచిస్తాం.
|z| = r = \(\sqrt{x^2+y^2}\)
Re(z) = r cos θ ⇔ x = r cos θ …..(1)
మరియు Im(z) = r sin θ ⇔ y = r sin θ ……(2)
(1), (2) ల నుండి ‘θ’ ను కనుగొందుము. θ ∈ (-π, π) ను θ కు ప్రధాన ఆయామము అంటారు.
0 = 0 + i0 యొక్క ఆయామము నిర్వచించలేము. Z యొక్క ఆయామము ఏకైకము కాదు.
2nπ + θ, n ∈ z కూడ z కు ఆయామమే.
మరియు -π < θ ≤ π విలువను z యొక్క ప్రధాన ఆయామం అందురు. దీనిని amp(z) లేదా Arg(z) గా సూచించెదరు.

→ సంకీర్ణ సంఖ్యకు సంయుగ్మం: x, y ∈ R మరియు ఏదేని సంకీర్ణ సంఖ్య z = x + iy కు సంయుగ్మం x + i(-y) ⇒ x – iy అని నిర్వచించి, \(\bar{z}\) తో సూచిస్తాం. ఏదేని సంకీర్ణ సంఖ్య మరియు వీని సంయుగ్మముల లబ్దము మరియు మొత్తములు ఖచ్చితముగా వాస్తవములు.

→ మాపము, ఆయామం మరియు సంయుగ్మ సంకీర్ణ సంఖ్యలు కొన్ని ధర్మములు:

• │\(\bar{z}\)│= |z|
• z + \(\bar{z}\) = 2 Re(z) మరియు z – \(\bar{z}\) = 2 Im(z)
• \(\overline{z_1 z_2}=\overline{z_1} \overline{z_2}\)
• \(\left(\frac{\overline{z_1}}{z_2}\right)=\frac{\bar{z}_1}{\bar{z}_2^{\prime}}\left|\frac{z_1}{z_2}\right|=\frac{\left|z_1\right|}{\left|z_2\right|}\), (z₂ ≠ 0), |z₁z₂| = |z₁| |z₂|
• \(z \bar{z}=|z|^2\) మరియు z ≠ 0, z-1 = \(\frac{\bar{z}}{|z|^2}\)
• z = |\(\bar{z}\)|; amp(\(\bar{z}\)) = 2π – amp(z)
• |z₁ + z₂| ≤ |z₁| + |z₂|, |z₁ – z₂| ≤ |z₁| + |z₂|
• |z₁ – z₂| ≥ ||z₁| – |z₂||
• amp (z₁) – amp (z₂) = 2π యొక్క ధన పూర్ణాంకముల లబ్ధము అయిన (vii) మరియు (viii) లు వాస్తవములు.
• amp (z₁z₂) = amp (z₁) + amp (z₂) + nπ, n ∈ {-1, 0, 1}
• amp(\(\frac{z_1}{z_2}\)) = amp (z₁) – amp (z₂) + nπ, n ∈ {-1, 0, 1}
• \(\frac{1}{{cis} \alpha}\) = cis (-α)
• cis α . cis β = cis(α + β)
• \(\frac{{cis} \alpha}{{cis} \beta}\) = cis(α – β)

→ డిమోయర్ సిద్ధాంతము:

• ‘n’ ఏదేని పూర్ణాంకం అయితే (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ
• n అకరణీయ సంఖ్య అయితే (cos θ + i sin θ)ⁿ కు ఒక విలువ cos nθ + i sin nθ
• z₀ = r₀ cis θ₀ ≠ 0 అయితే \(z_0^{1 / n}=r_0^{1 / n} {cis}\left(\frac{2 k \pi+\theta_0}{n}\right)\), k = 0, 1, 2, ……., (n – 1)

→ ఒకటి యొక్క ఘనమూలాలు:

• ఏకకపు ఘనమూలాలు 1, ω = \(\frac{-1+\sqrt{3 i}}{2}\) మరియు ω² = \(\frac{-1-\sqrt{3 i}}{2}\)
• 1 + ω + ω² = 0 మరియు ω³ = 1; 1 + ω = -ω², 1 + ω² = -1
• ఒకటి వాస్తవము గాని విలువలు ఒకటి మరియొక దాని వర్గమునకు సమానమగును.
• ఒకటి యొక్క వాస్తవముగాని విలువలు α, β అయిన α + β = -1, αβ = 1, α² = -β, β² = α మరియు α³ = β³ = 1
• \((-1)^{1 / 3}\) మూలాలు -1, -ω, -ω²

సూత్రాలు:
→ z యొక్క మాపము = \(\sqrt{x^2+y^2}\)

→ \(\sqrt{a+i b}\) = (x + iy) అయిన

• \(\sqrt{a+i b}+\sqrt{a-i b}=\sqrt{2 a+2 \sqrt{a^2+b^2}}\)
• \(\sqrt{a+i b}-\sqrt{a-i b}=i \sqrt{2 \sqrt{a^2+b^2-2 a}}\)

→ a + ib యొక్క సంయుగ్మము = a – ib

→ a – ib యొక్క సంయుగ్మము = a + ib

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 10 యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు Exercise 10(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 10 యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు Exercise 10(b)

అభ్యాసం – 10(బి)

I.

ప్రశ్న 1.
ఒక నాణేన్ని n సార్లు ఎగరవేసే ప్రయోగంలో, బొమ్మలు పడే సంఖ్యను, చలరాశి X సూచిస్తుంది. P(X = 4), P(X = 5), P(X = 6) లు అంకశ్రేఢి లో ఉన్నాయి. అప్పుడు n కనుక్కోండి.
సాధన:
X ద్విపద విభాజనాన్ని పాటిస్తుంది.
p = \(\frac{1}{2}\), q = \(\frac{1}{2}\) (∵ నాణేన్ని ఎగరవేస్తే)
Hint: a, b, c లు A.P. లో ఉంటే 2b = a + c (లేదా) b – a = c – a
P(X = 4), P(X = 5), P(X = 6) లు A.P. లో ఉన్నాయి.

⇒ 2 × 30(n – 4) = 5[30 + n² – 9n + 20]
⇒ 12n – 48 = n² – 9n – 50
⇒ n² – 21n + 98 = 0
⇒ n² – 14n – 7n + 98 = 0
⇒ n(n – 14) – 7(n – 14) = 0
⇒ (n – 7) (n – 14) = 0
∴ n = 7 లేదా 14

ప్రశ్న 2.
కనీసం ఒక బొమ్మ పడుతూ, సంభావ్యత కనీసం 0.8 కావడానికి, ఒక నిష్పాక్షిక నాణేన్ని ఎగరవేయాల్సిన గరిష్ఠ సంఖ్యను కనుక్కోండి.
సాధన:
ఒక నిష్పాక్షిక నాణేన్ని n సార్లు ఎగరవేసితిమి అనుకోండి.
బొమ్మల సంఖ్యను చలరాశి X సూచిస్తుంది.
X ద్విపద విభాజనాన్ని పాటిస్తుంది. n, p లు పరామితులు.
ఇచ్చట p = \(\frac{1}{2}\)
దత్తాంశం నుండి P(X ≥ 1) ≥ 0.8
⇒ 1 – P(X = 0) ≥ 0.8
⇒ P(X = 0) ≤ 0.2
⇒ \({ }^n C_o\left(\frac{1}{2}\right)^n\) ≤ 0.2
⇒ \(\left(\frac{1}{2}\right)^n \leq \frac{1}{5}\)
n ≥ ౩ అయిన పై అసమీకరణం సత్యం కనుక n గరిష్ఠ విలువ 3.

ప్రశ్న 3.
ఒక బాంబు, ఒక వంతెనను కూల్చివేసే సంభావ్యత \(\frac{1}{2}\), వంతెనను కూల్చడానికి 3 సార్లు (వరుసగా కానవసరం లేదు) నేరుగా కొట్టవలసి వస్తుంది. వంతెన కూలే సంభావ్యత 0.9 కంటే ఎక్కువ కావడానికి కావలసిన బాంబుల కనిష్ట సంఖ్యను కనుక్కోండి.
సాధన:
వంతెనను కూల్చడానికి కావలసిన బాంబుల కనిష్ట సంఖ్య n, యాదృచ్ఛిక చలరాశి X బాంబుల సంఖ్యను తెలిపితే,
p = \(\frac{1}{2}\)
ఇప్పుడు P(X ≥ 3) > 0.9
⇒ 1 – P(X < 3) > 0.9
⇒ P(X < 3) < 0.1
⇒ P(X = 0) + P(X = 1) + P (X = 2) < 0.1


⇒ 5(n² + n + 2) < 2n
యత్నదోష పద్ధతిన n ≥ 9 పై అసమీకరణాన్ని తృప్తి పరుస్తుంది.
∴ కనిష్ట విలువ 9.

ప్రశ్న 4.
ఒక ద్విపద చలరాశి మధ్యమం, విస్తృతుల మధ్య భేదం \(\frac{5}{9}\) అయితే, ప్రయోగాన్ని 5 సార్లు నిర్వహించినప్పుడు 2 సార్లు సఫలం అయ్యే ఘటన సంభావ్యతను కనుక్కోండి.
సాధన:
n = 5, p లు ద్విపద విభాజనానికి పరామితులు
మధ్యమం – విస్తృతి = \(\frac{5}{9}\)

∴ 2 సార్లు సఫలం అయ్యే ఘటన సంభావ్యత = \(\frac{80}{243}\)

ప్రశ్న 5.
ప్రయాణానికి సంసిద్ధమైన 9 ఓడలలో ఒకటి మునిగిపోయే ప్రమాదం ఉంది. 6 ఓడలు ప్రయాణానికి సంసిద్ధమైతే (i) కనీసం ఒకటి క్షేమంగా చేరడానికి (ii) సరిగ్గా 3 క్షేమంగా చేరడానికి గల సంభావ్యతలను కనుగొనండి. [Mar. ’08]
సాధన:
p = ఓడ మునిగిపోవటానికి సంభావ్యత = \(\frac{1}{9}\)
q = 1 – p
= 1 – \(\frac{1}{9}\)
= \(\frac{8}{9}\)
ఓడల సంఖ్య = n = 6

ప్రశ్న 6.
ఒక ద్విపద చలరాశి X అంకమధ్యం, విస్తృతులు వరుసగా 2.4, 1.44 అయితే, P(1 < X ≤ 4) ను కనుక్కోండి. [May ’06]
సాధన:
X అంకమధ్యమం = np = 2.4 ……(1)
విస్తృతి = npq = 1.44 ………(2)
(2) ను (1) చే భాగించగా
\(\frac{n p q}{n p}=\frac{1.44}{2.4}\)
q = 0.6 = \(\frac{3}{5}\)
p = 1 – q
= 1 – 0.6
= 0.4
= \(\frac{2}{5}\)
(1) లో వ్రాయగా
n(0.4) = 2.4
n = \(\frac{2.4}{0.4}\) = 6
P(1 < X ≤ 4) = P(X = 2) + P(X = 3) + P(X = 4)

ప్రశ్న 7.
ఒక కంపెనీ తయారు చేసే విద్యుత్ (ఎలక్ట్రిక్) బల్బులలో 10 శాతం లోపం ఉన్నవని ఇచ్చారు. 20 బల్బులలో 2 కంటే ఎక్కువ బల్బులు లోపం ఉన్నవి కాగల సంభావ్యతను కనుక్కోండి.
సాధన:
p = బల్బు లోపం కలది కావటానికి సంభావ్యత = \(\frac{1}{10}\)
q = 1 – p
= 1 – \(\frac{1}{10}\)
= \(\frac{9}{10}\)
n = బల్బుల సంఖ్య = 20
P(X > 2) = 1 – P(X ≤ 2)
= 1 – [P(X = 0) + P(X = 1) + P(X = 2)]

ప్రశ్న 8.
సగటున ప్రతి 30 రోజులలో 12 రోజులు వర్షం కురిస్తే, ఒక వారంలో 3 రోజులు వర్షం కురిసే సంభావ్యతను కనుక్కోండి.
సాధన:
p = \(\frac{12}{30}=\frac{2}{5}\) (దత్తాంశము నుండి)
q = 1 – p
= 1 – \(\frac{2}{5}\)
= \(\frac{3}{5}\)
n = 7, r = 3
వారంలో 3 రోజులు వర్షం కురిసే సంభావ్యత P(X = 3)

ప్రశ్న 9.
అంకమధ్యమం 6, విస్తృతి 2 గల ఒక ద్విపద విభాజనం లోని మొదటి రెండు పదాలను కనుక్కోండి.
సాధన:
n, p లు ద్విపద విభాజన పరిమితులు.
మధ్యమం (np) = 6 …..(1)
విస్తృతి (npq) = 2 …..(2)
అప్పుడు \(\frac{\mathrm{npq}}{\mathrm{np}}=\frac{2}{6}\)
q = \(\frac{1}{3}\)
p = 1 – q
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
(1) నుండి nP = 6
n(\(\frac{2}{3}\)) = 6
n = \(\frac{18}{2}\) = 9
విభాజనంలో మొదటి పదం P(X = 0) = \({ }^9 C_0\left(\frac{1}{3}\right)^9=\frac{1}{3^9}\)
రెండవ పదం P(X = 1) = \({ }^9 C_1\left(\frac{1}{3}\right)^8\left(\frac{2}{3}\right)=\frac{2}{3^7}\)

ప్రశ్న 10.
ఒక నగరంలో 50 రోజుల వ్యవధిలో 10 ప్రమాదాలు సంభవిస్తాయి. ప్రమాదాల సంఖ్య ఒక పాయిజాన్ విభాజనాన్ని అనుసరిస్తుందనుకుంటే, ఒక్క రోజులో 3 లేదా అంతకంటే ఎక్కువ ప్రమాదాలు జరగగల సంభావ్యతను కనుక్కోండి.
సాధన:
రోజులో సగటు ప్రమాదాల సంఖ్య
λ = \(\frac{10}{50}=\frac{1}{5}\) = 0.2
రోజులో 3 లేదా అంతకంటే ఎక్కువ ప్రమాదాలు జరగగల సంభావ్యత
P(X ≥ 3) = \(\sum_{k=3}^{\infty} \mathrm{e}^{-\lambda} \cdot \frac{\lambda^k}{k !}\), λ = 0.2

II.

ప్రశ్న 1.
5 నాణేలను 320 సార్లు ఎగరవేశారు. బొమ్మల సంఖ్యకు పౌనఃపున్య విభాజనాన్ని కనుక్కుని, ఫలితాన్ని పట్టికగా రాయండి.
సాధన:
5 నాణేలను 320 సార్లు ఎగరవేశారు.
బొమ్మ రావడానికి సంభావ్యత
p = \(\frac{1}{2}\)
n = 5
q = 1 – p
= 1 – \(\frac{1}{2}\)
= \(\frac{1}{2}\)
X బొమ్మలు రావటానికి సంభావ్యత

ప్రశ్న 2.
ఒక ప్రశ్నాపత్రంలోని 10 సమాధానాలకు కనీసం సరైనవిగా ఊహించగల సంభావ్యత కింది సందర్భాలలో కనుక్కోండి. [Mar. ’14]
(i) ప్రశ్నాపత్రంలో తప్పు, ఒప్పులు గల ప్రశ్నలు ఉన్నప్పుడు
(ii) ప్రశ్నాపత్రంలో 4 ఐచ్ఛిక సమాధానాలుండే బహుళైచ్ఛిక ప్రశ్నలున్నప్పుడు
సాధన:
(i) ఒప్పు లేదా తప్పులు సమాధానాలు కనుక
సఫల సంభావ్యత p = \(\frac{1}{2}\)
విఫల సంభావ్యత q = \(\frac{1}{2}\)
10 సమాధానాలలో 6 సరియైనట్టివిగా ఊహించగల సంభావ్యత
P(X = 6) = \({ }^{10} C_6\left(\frac{1}{2}\right)^{10-6}\left(\frac{1}{2}\right)^6\)
= \({ }^{10} C_6\left(\frac{1}{2}\right)^{10}\)

(ii) 4 సాధ్యమయ్యే సమాధానాలు ఉన్న ప్రశ్నలు
కనుక సఫల సంభావ్యత p = \(\frac{1}{4}\)
విఫల సంభావ్యత q = \(\frac{3}{4}\)
10 సమాధానాలలో 6 సరియైనట్టివిగా ఊహించగల సంభావ్యత
P(X = 6) = \({ }^{10} C_6\left(\frac{3}{4}\right)^{10-6}\left(\frac{1}{4}\right)^6\)
= \({ }^{10} C_6 \cdot \frac{3^4}{4^{10}}\)

ప్రశ్న 3.
ఒక నిముషంలో ఒక సినిమా టికెట్ కౌంటర్ వద్దకు వచ్చి చేరే వ్యక్తుల సంఖ్య, 6 పరామితితో ఒక పాయిజాన్ విభాజనంగా ఉంటుంది.
(i) ఒక నిర్దిష్ట నిమిషంలో ఏ ఒక్కరూ క్యూలో చేరని
(ii) ఒక నిమిషంలో ఇద్దరు లేదా అంతకంటే ఎక్కువ మంది క్యూలో వచ్చి చేరే సంభావ్యతలను కనుక్కోండి.
సాధన:
λ = 6
(i) ఒక నిర్దిష్ట నిమిషంలో ఏ ఒక్కరూ క్యూలో చేరని సంభావ్యత
P(X = 0) = \(\frac{\mathrm{e}^{-\lambda} \lambda^0}{0 !}\) = e-6

(ii) ఒక నిముషంలో ఇద్దరూ లేదా అంతకంటే ఎక్కువ మంది క్యూలో వచ్చి చేరే సంభావ్యత
P(X ≥ 2) = 1 – P(X ≤ 1)
= 1 – [P(X = 0) + P(X = 1)]
= 1 – \(\left[\mathrm{e}^{-\lambda} \frac{\lambda^0}{0 !}+\frac{e^{-\lambda} \cdot \lambda^1}{1 !}\right]\)
= 1 – \(\left[\mathrm{e}^{-6}+\frac{\mathrm{e}^{-6} \cdot(6)}{1 !}\right]\)
= 1 – 7e^-6

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 10 యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు Exercise 10(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 10 యాదృచ్ఛిక చలరాశలు, సంభావ్యత విభాజనాలు Exercise 10(a)

అభ్యాసం – 10(ఎ)

I.

ప్రశ్న 1.
ఒక విచ్ఛిన్న యాదృచ్ఛిక చలరాశి సంభావ్యతా విభాజన ప్రమేయం, x = 0, 1, 2 బిందువుల వద్ద మినహా తక్కిన అన్ని చోట్ల సున్న అవుతుంది. ఈ బిందువుల వద్ద, దాని విలువ P(0) = 3c³, P(1) = 4c – 10c², P(2) = 5c – 1, c > 0. c విలువ కనుక్కోండి.
సాధన:
P(X = 0) + P(X = 1) + P(X = 2) = 1
⇒ 3c³ + 4c – 10c² + 5c – 1 = 1
⇒ 3c³ – 10c² + 9c – 2 = 0
⇒ (c – 1) (c – 2) (3c – 1) = 0
⇒ c = 1 లేదా 2 లేదా \(\frac{1}{3}\)
c = 1, 2 అయిన P(0) > 1
∴ c = \(\frac{1}{3}\)

ప్రశ్న 2.
F(x) = \(c\left(\frac{2}{3}\right)^x\), x = 1, 2, 3 …….. ఒక విచ్ఛిన్న యాదృచ్ఛిక చలరాశి X సంభావ్యతా విభాజన ప్రమేయాన్ని తృప్తిపరచేటట్లుగా, స్థిరరాశి c విలువను కనుక్కోండి.
సాధన:
దత్తాంశం నుండి

ప్రశ్న 3.

అనేది ఒక యాదృచ్ఛిక చలరాశి X సంభావ్యతా విభాజనం k విలువ, X విస్తృతులను కనుక్కోండి. [Mar.’06]
సాధన:
సంభావ్యతల మొత్తం = 1
⇒ 0.1 + k + 0.2 + 2k + 0.3 + k = 1
⇒ 4k + 0.6 = 1
⇒ 4k = 1 – 0.6 = 0.4
⇒ k = \(\frac{0.4}{4}\) = 0.1
అంకమాధ్యమం (μ) = (-2) (0.1) + (-1) (k) + 0(0.2) + 1(2k) + 2(0.3) + 3k
= -0.2k + 0 + 2k + 0.6 + 3k
= 4k + 0.4
=4(0.1) + 0.4
= 0.4 + 0.4
= 0.8
μ = 0.8
విస్తృతి (σ²) = \(\sum_{i=1}^n x_i^2 P\left(x=x_i\right)\) – μ²
∴ విస్తృతి = 4(0.1) + 1(k) + 0(0.2) + 1(2k) + 4(0.3) + 9k – μ²
= 0.4 + k + 0 + 2k + 4(0.3) + 9k – μ²
= 12k + 0.4 + 1.2 – (0.8)²
= 12(0.1) + 1.6 – 0.64
= 1.2 + 1.6 – 0.64
∴ σ² = 2.8 – 0.64 = 2.16

ప్రశ్న 4.

అనేది ఒక యాదృచ్ఛిక చలరాశి X సంభావ్యతా విభాజనం. అయితే X విస్తృతిని కనుక్కోండి.
సాధన:

ప్రశ్న 5.
ఒక యాదృచ్ఛిక చలరాశి X సంభావ్యతా విభాజనం ఈ క్రింది విధంగా ఉంది. [A.P. & T.S. Mar. ’16]

(i) k విలువ (ii) X అంకమధ్యమం (iii) P(0 < x < 5) లను కనుక్కోండి.
సాధన:
సంభావ్యతల మొత్తం = 1
⇒ 0 + k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
⇒ 10k² + 9k = 1
⇒ 10k² + 9k – 1 = 0
⇒ 10k² + 10k – k – 1 = 0
⇒ 10k(k + 1) – 1(k + 1) = 0
⇒ (10k – 1) (k + 1) = 0
⇒ k = \(\frac{1}{10}\), -1
∵ k > 0
∴ k = \(\frac{1}{10}\)
(i) k = \(\frac{1}{10}\)
(ii) X అంక మధ్యమం (μ) = \(\sum_{i=1}^n x_i P\left(x=x_i\right)\)
∴ μ = 0(0) + 1(k) + 2(2k) + 3(2k) + 4(3k) + 5(k²) + 6(2k²) + 7(7k² + k)
= 0 + k + 4k + 6k + 12k + 5k² + 12k² + 49k² + 7k
= 66k² + 30k
= \(66\left(\frac{1}{100}\right)+30 \times\left(\frac{1}{10}\right)\)
= 0.66 + 3
= 3.66
(iii) P(0 < x < 5)
P(0 < x < 5) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= k + 2k + 2k + 3k
= 8k
= 8 × \(\frac{1}{10}\)
= \(\frac{4}{5}\)

II.

ప్రశ్న 1.
ఒక యాదృచ్ఛిక చలరాశి వ్యాప్తి X = {0, 1, 2}. P(X = 0) = 3c³, P(X = 1) = 4c – 10c², P(X = 2) = 5c – 1 అయినప్పుడు (i) c విలువ (ii) P(X < 1), P(1 < X ≤ 2), P(0 < X ≤ 3) లను కనుక్కోండి. [Mar. ’13, ’11, ’07, ’05; May ’11]
సాధన:
P(X = 0) + P(X = 1) + P(X = 2) = 1
⇒ 3c³ + 4c – 10c² + 5c – 1 = 1
⇒ 3c³ – 10c² + 9c – 2 = 0
⇒ (c – 1) (c – 2) (3c – 1) = 0
⇒ c = 1 లేదా 2 లేదా \(\frac{1}{3}\)
c = 1, 2 అయిన P(X = 0) > 1
∴ c = \(\frac{1}{3}\)
(i) P(X < 1) = P(X = 0)
= 3 . c³
= 3 . \(\left(\frac{1}{3}\right)^3\)
= \(\frac{1}{9}\)
(ii) P(1 < X ≤ 2) = P(X = 2)
= 5c – 1
= \(\frac{5}{3}\) – 1
= \(\frac{2}{3}\)
(iii) P(0 < x ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3)
= 4c – 10c² + 5c – 1 + 0
= 9c – 10c² – 1
= \(\text { 9. } \frac{1}{3}-10 \cdot \frac{1}{9}-1\)
= \(\frac{8}{9}\)

ప్రశ్న 2.
ఒక యాదృచ్ఛిక చలరాశి X వ్యాప్తి (1, 2, 3, ………} P(X = K) = \(\frac{c^{\mathbf{k}}}{k !}\); (k = 1, 2, 3,…) అయితే c విలువను, P(0 < X < 3) ని కనుక్కోండి.
సాధన:
సంభావ్యతల మొత్తం = 1