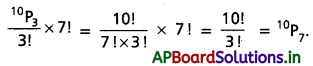Inter 2nd Year

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(b)

అభ్యాసం – 7 (బి)

క్రింది భిన్నాలను పాక్షిక భిన్నాలుగా విడగొట్టండి.

ప్రశ్న 1.
\(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}\) [May, Mar. ’11]
సాధన:
\(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+2}\) అనుకుందాం.
2x² + 3x + 4 = A(x² + 2) + (Bx + C) (x – 1) …….(1)
x = 1 వ్రాస్తే, 2 + 3 + 4 = A(1 + 2)
⇒ 9 = 3A
⇒ A = 3
(1) లో x² గుణకాలను పోల్చగా
2 = A + B
⇒ B = 2 – A
⇒ B = 2 – 3
⇒ B = -1
(1) లో స్థిరపదాలను పోల్చగా
4 = 2A – C
⇒ C = 2A – 4
= 6 – 4
= 2
∴ A = 3, B = -1, C = 2
\(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{3}{x-1}+\frac{-x+2}{x^2+2}\)

ప్రశ్న 2.
\(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}\)
సాధన:
\(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}=\frac{A}{2+x}+\frac{B x+C}{1-x+x^2}\) అనుకుందాం.
3x – 1 = A(1 – x + x²) (Bx + C) (2 + x) …….(1)
x = -2 వ్రాస్తే, -7 = A(1 + 2 + 4)
⇒ -7 = 7A
⇒ A = -1
(1) లో x² గుణకాలను పోల్చగా
0 = A + B
⇒ B = -A = 1
స్థిరపదాలను పోల్చగా
-1 = A + 2C
⇒ 2C = -1 – A
⇒ 2C = -1 + 1
⇒ 2C = 0
⇒ C = 0
∴ A = -1, B = 1, C = 0
\(\frac{3 x-1}{\left(1-x+x^2\right)(2+x)}=-\frac{1}{2+x}+\frac{x}{1-x+x^2}\)

ప్రశ్న 3.
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}\)
సాధన:
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{A}{x+2}+\frac{B x+C}{x^2+1}\) అనుకుందాం.
x² – 3 = A(x² + 1) + (Bx + C) (x + 2) …..(1)
x = -2 వ్రాస్తే, 4 – 3 = A(4 + 1)
⇒ 1 = 5A
⇒ A = \(\frac{1}{5}\)
(1) లో x² గుణకాలను పోల్చగా
1 = A + B
⇒ B = 1 – A
⇒ B = 1 – \(\frac{1}{5}\)
⇒ B = \(\frac{4}{5}\)
(1) లో స్థిరపదాలను పోల్చగా
-3 = A + 2C
⇒ 2C = -3 – A
⇒ 2C = -3 – \(\frac{1}{5}\)
⇒ 2C = \(-\frac{16}{5}\)
⇒ C = \(-\frac{8}{5}\)
∴ A = \(\frac{1}{5}\), B = \(\frac{4}{5}\), C = \(-\frac{8}{5}\)
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{1}{5(x+2)}+\frac{4 x-8}{5\left(x^2+1\right)}\)

ప్రశ్న 4.
\(\frac{x^2+1}{\left(x^2+x+1\right)^2}\)
సాధన:
\(\frac{x^2+1}{\left(x^2+x+1\right)^2}=\frac{A x+B}{x^2+x+1}+\frac{C x+D}{\left(x^2+x+1\right)^2}\) అనుకుందాం.
x² + 1 = (Ax + B) (x² + x + 1) + (Cx + D) ……(1)
(1) లో x³ గుణకాలను పోల్చగా, A = 0
(1) లో x² గుణకాలను పోల్చగా, A + B = 1 ⇒ B = 1
(1) లో x గుణకాలను పోల్చగా, A + B + C = 0
⇒ 1 + C = 0
⇒ C = -1
(1) లో స్థిరపదాలను పోల్చగా, B + D = 1
⇒ D = 1 – B
= 1 – 1
= 0
∴ A = 0, B = 1, C = -1, D = 0
∴ Ax + B = 1, Cx + D = -x
∴ \(\frac{x^2+1}{\left(x^2+x+1\right)^2}=\frac{1}{x^2+x+1}-\frac{x}{\left(x^2+x+1\right)^2}\)

ప్రశ్న 5.
\(\frac{x^3+x^2+1}{(x-1)\left(x^3-1\right)}\)
సాధన:

∴ x³ + x² + 1 = A(x – 1) (x² + x + 1) + B(x² + x + 1) + (Cx + D) (x – 1)² ……(2)
x = 1 ను (2) లో వ్రాయగా
1 + 1 + 1 = A(0) + B(1 + 1 + 1) + (C(1) + D) (0)
⇒ 3B = 3
⇒ B = 1
(2) లో x³ గుణకాలను పోల్చగా
1 = A + C ….(3)
(2) లో x² గుణకాలను పోల్చగా
1 = A(1 – 1) + B(1) + C(-2) + D(1)
⇒ 1 = B – 2C + D
⇒ 1 = 1 – 2C + D
⇒ 2C = D ……..(4)
x = 0 ను (2) లో వ్రాయగా
1 = A(-1) (1) + B(1) + D(-1)²
⇒ A + B + D = 1
⇒ -A + 1 + D = 1
⇒ A = D ……..(5)
(3), (4), (5) ల నుండి
1 = D + \(\frac{D}{2}\)
⇒ \(\frac{3D}{2}\) = 1
⇒ D = \(\frac{2}{3}\)
(5) నుండి A = \(\frac{2}{3}\)
(4) నుండి C = \(\frac{\mathrm{D}}{2}=\frac{\left(\frac{2}{3}\right)}{2}=\frac{1}{3}\)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(a)

అభ్యాసం – 7(ఎ)

I. క్రింది భిన్నాలను పాక్షిక భిన్నాలుగా విడగొట్టండి.

ప్రశ్న 1.
\(\frac{2 x+3}{(x+1)(x-3)}\)
సాధన.
\(\frac{2 x+3}{(x+1)(x-3)}=\frac{A}{x+1}+\frac{B}{x-3}\) అనుకుందాం.
∴ 2x + 3 = A(x – 3) + B(x + 1) …..(1)
(1) లో x = -1 వ్రాస్తే, 1 = A(-4) ⇒ A = \(-\frac{1}{4}\)
(1) లో x = 3 వ్రాస్తే, 9 = B(4) ⇒ B = \(\frac{9}{4}\)
\(\frac{2 x+3}{(x+1)(x-3)}=\frac{-1}{4(x+1)}+\frac{9}{4(x-3)}\)

ప్రశ్న 2.
\(\frac{5 x+6}{(2+x)(1-x)}\)
సాధన:
\(\frac{5 x+6}{(2+x)(1-x)}=\frac{A}{2+x}+\frac{B}{1-x}\) అనుకుందాం.
5x + 6 = A(1 – x) + B(2 + x) …..(1)
(1) లో x = -2 వ్రాస్తే, -10 + 6 = A(1 + 2) ⇒ A = \(-\frac{4}{3}\)
(1) లో x = 1 వ్రాస్తే, 5 + 6 = B(2 + 1) ⇒ B = \(\frac{11}{3}\)
∴ \(\frac{5 x+6}{(2+x)(1-x)}=-\frac{4}{3(2+x)}+\frac{11}{3(1-x)}\)

II.

ప్రశ్న 1.
\(\frac{3 x+7}{x^2-3 x+2}\)
సాధన:
\(\frac{3 x+7}{x^2-3 x+2}=\frac{3 x+7}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}\) అనుకుందాం.
3x + 7 = A(x – 2) + B(x – 1) ……(1)
(1) లో x = 1 వ్రాస్తే, 10 = -A ⇒ A = -10
(1) లో x = 2 వ్రాస్తే, 13 = B
∴ \(\frac{3 x+7}{x^2-3 x+2}=\frac{-10}{x-1}+\frac{13}{x-2}\)

ప్రశ్న 2.
\(\frac{x+4}{\left(x^2-4\right)(x+1)}\) [Mar. ’14]
సాధన:
\(\frac{x+4}{\left(x^2-4\right)(x+1)}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{x-2}\)
x + 4 = A(x2 – 4) + B(x + 1)(x – 2) + C(x + 1)(x + 2) …….(1)
(1) లో x = -1 వ్రాస్తే, 3 = A(1 – 4)
⇒ 3 = -3A
⇒ A = -1
(1) లో x = -2 వ్రాస్తే,
2 = B(-2 + 1) (-2 – 2)
⇒ 2 = 4B
⇒ B = \(\frac{1}{2}\)
(1) లో x = 2 వ్రాస్తే,
6 = C(2 + 1) (2 + 2)
⇒ 6 = 12C
⇒ C = \(\frac{1}{2}\)
∴ \(\frac{x+4}{\left(x^2-4\right)(x+1)}=-\frac{1}{x+1}+\frac{1}{2(x+2)}+\frac{1}{2(x-2)}\)

ప్రశ్న 3.
\(\frac{2 x^2+2 x+1}{x^3+x^2}\)
సాధన:
\(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{2 x^2+2 x+1}{x^2(x+1)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+1}\)
2x² + 2x + 1 = Ax(x + 1) + B(x + 1) + Cx² ……(1)
(1) లో x = 0 వ్రాస్తే, 1 = B
(1) లో x = -1 వ్రాస్తే, 2 – 2 + 1 = C(1) ⇒ C = 1
ఇరువైపులా x² గుణకాలు పోల్చగా
2 = A + C
⇒ A = 2 – C
= 2 – 1
= 1
∴ \(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\)

ప్రశ్న 4.
\(\frac{2 x+3}{(x-1)^3}\)
సాధన:
\(\frac{2 x+3}{(x-1)^3}\)
x – 1 = y అనుకుంటే x = y + 1
⇒ \(\frac{2 x+3}{(x-1)^3}=\frac{2(y+1)+3}{y^3}=\frac{2 y+5}{y^3}\)

ప్రశ్న 5.
\(\frac{x^2-2 x-6}{(x-2)^3}\)
సాధన:
x – 2 = y అనుకొనుము
⇒ x = y + 2

III.

ప్రశ్న 1.
\(\frac{x^2-x+1}{(x+1)(x-1)^2}\)
సాధన:
\(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{A}{x+1}+\frac{B}{x-1}+\frac{C}{(x-1)^2}\) అనుకుందాం.
x² – x + 1 = A(x – 1)² + B(x + 1)(x – 1) + C(x + 1) …….(1)
x = -1 వ్రాస్తే, 1 + 1 + 1 = A(4) ⇒ A = \(\frac{3}{4}\)
x = 1 వ్రాస్తే, 1 – 1 + 1 = C(2) ⇒ C = +\(\frac{1}{2}\)
1 లో x² గుణకాలను పోల్చగా
A + B = 1
⇒ B = 1 – A
⇒ B = 1 – \(\frac{3}{4}\)
⇒ B = \(\frac{1}{4}\)
∴ \(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{3}{4(x+1)}+\frac{1}{4(x-1)}+\frac{1}{2(x-1)^2}\)

ప్రశ్న 2.
\(\frac{9}{(x-1)(x+2)^2}\)
సాధన:
\(\frac{9}{(x-1)(x+2)^2}=\frac{A}{x-1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}\) అనుకొందాం.
9 = A(x + 2)² + B(x – 1) (x + 2) + C(x – 1) ……(1)
x = 1 వ్రాస్తే, 9 = 9A ⇒ A = 1
x = -2 వ్రాస్తే, 9 = -3C ⇒ C = -3
(1) లో x² గుణకాలను పోల్చగా
A + B = 0
⇒ B = -A = -1
∴ \(\frac{9}{(x-1)(x+2)^2}=\frac{1}{x-1}-\frac{1}{x+2}-\frac{3}{(x+2)^2}\)

ప్రశ్న 3.
\(\frac{1}{(1-2 x)^2(1-3 x)}\)
సాధన:
\(\frac{1}{(1-2 x)^2(1-3 x)}=\frac{A}{1-3 x}+\frac{B}{1-2 x}+\frac{C}{(1-2 x)^2}\) అనుకుందాం.
1 = A(1 – 2x)² + B(1 – 3x) (1 – 2x) + C(1 – 3x) ……..(1)
x = \(\frac{1}{3}\) వ్రాస్తే, 1 = A\(\left(1-\frac{2}{3}\right)^2\)
⇒ 1 = \(\frac{A}{9}\)
⇒ A = 9
x = \(\frac{1}{2}\) వ్రాస్తే, 1 = C(1 – \(\frac{3}{2}\))
⇒ 1 = \(-\frac{C}{2}\)
⇒ C = -2
(1) లో x² గుణకాలను పోల్చగా
0 = 4A + 6B
6B = -4A – 36
B = -6
∴ \(\frac{1}{(1-2 x)^2(1-3 x)}=\frac{9}{1-3 x}-\frac{6}{1-2 x}-\frac{2}{(1-2 x)^2}\)

ప్రశ్న 4.
\(\frac{1}{x^3(x+a)}\)
సాధన:
\(\frac{1}{x^3(x+a)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x^3}+\frac{D}{x+a}\) అనుకుందాం.
= \(\frac{A \cdot x^2(x+a)+B(x)(x+a)+C(x+a)+D x^3}{x^3(x+a)}\)
∴ 1 = A(x²) (x + a) + Bx(x + a) + C(x + a) + Dx³ ……..(1)
x = 0 ను (1) లో వ్రాస్తే, 1 = A(0) + B(0) + C(0 + a) + D(0)
⇒ 1 = C (a)
⇒ C = \(\frac{1}{a}\)
x = -a ను (1) లో వ్రాస్తే, 1 = A(0) + B(0) + C(0) + D(-a)³
⇒ 1 = D(-a³)
⇒ D = \(-\frac{1}{a^3}\)
(1) లో x³ గుణకాలను పోల్చగా
0 = A + D
⇒ A = -D
⇒ A = \(\frac{1}{a^3}\)
(1) లో x² గుణకాలను పోల్చగా
0 = Aa + B
⇒ B = -aA
⇒ B = \(-a\left(\frac{1}{a^3}\right)\)
⇒ B = \(-\frac{1}{a^2}\)

ప్రశ్న 5.
\(\frac{x^2+5 x+7}{(x-3)^3}\)
సాధన:

ప్రశ్న 6.
\(\frac{3 x^3-8 x^2+10}{(x-1)^4}\)
సాధన:

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(c) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(c)

అభ్యాసం – 6(సి)

ప్రశ్న 1.
క్రింది సమాసాల విలువలను 4 దశాంశాలకు సవరించి కనుక్కోండి.
(i) \(\sqrt[5]{242}\)
సాధన:

(ii) \(\sqrt[7]{127}\)
సాధన:

(iii) \(\sqrt[5]{32.16}\)
సాధన:

(iv) √199
సాధన:

(v) \(\sqrt[3]{1002}-\sqrt[3]{998}\)
సాధన:

(vi) \((1.02)^{3 / 2}-(0.98)^{3 / 2}\)
సాధన:

= 2[0.0299995]
= 0.0599990
≈ 0.059999
∴ \((1.02)^{3 / 2}-(0.98)^{3 / 2}\) = 0.059999

ప్రశ్న 2.
x² ఆపై x ఘాతాలు ఉపేక్షించేంతగా |x| స్వల్పమైతే క్రింది సమాసాల ఉజ్జాయింపు విలువలను కనుక్కోండి.
(i) \(\frac{(4+3 x)^{1 / 2}}{(3-2 x)^2}\)
సాధన:

(ii) \(\frac{\left(1-\frac{2 x}{3}\right)^{3 / 2}(32+5 x)^{1 / 5}}{(3-x)^3}\)
సాధన:

(iii) \(\sqrt{4-x}\left(3-\frac{x}{2}\right)^{-1}\)
సాధన:

(iv) \(\frac{\sqrt{4+x}+\sqrt[3]{8+x}}{(1+2 x)+(1-2 x)^{-1 / 3}}\)
సాధన:

(v) \(\frac{(8+3 x)^{2 / 3}}{(2+3 x) \sqrt{4-5 x}}\)
సాధన:

ప్రశ్న 3.
s, t లు ధన వాస్తవసంఖ్యలు, s తో పోల్చినపుడు t విలువ చాలా తక్కువ అయితే \(\left(\frac{s}{s+t}\right)^{1 / 3}-\left(\frac{s}{s-t}\right)^{1 / 3}\) యొక్క ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:
s తో పోల్చినపుడు విలువ చాలా తక్కువ కనుక \(\frac{t}{s}\) అత్యల్పం
∴ |\(\frac{t}{s}\)| < 1

ప్రశ్న 4.
p, q లు ధన వాస్తవ సంఖ్యలు, q తో సరి పోలిస్తే p విలువ చాలా తక్కువ అయితే \(\left(\frac{q}{q+p}\right)^{1 / 2}+\left(\frac{q}{q-p}\right)^{1 / 2}\) యొక్క ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:
q తో సరిపోలిస్తే p విలువ చాలా తక్కువ కనుక \(\frac{p}{q}\) అత్యల్పం

ప్రశ్న 5.
x⁴, ఆపై x ఘాతాలు ఉపేక్షిస్తే \(\sqrt[3]{x^2+64}-\sqrt[3]{x^2+27}\) యొక్క ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 6.
3√3 విలువను \(\frac{2}{3}\) యొక్క ఆరోహణ ఘాతాలలో వ్రాయండి.
సాధన:

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(b)

అభ్యాసం – 6(బి)

I.

ప్రశ్న 1.
క్రింది సమాసాలకు ద్విపద విస్తరణ వ్యవస్థితంచే x ల సమితులు కనుక్కోండి. [T.S. Mar. ’16, Mar. ’11]
(i) \((2+3 x)^{-2 / 3}\)
సాధన:

(ii) \((5+x)^{3 / 2}\)
సాధన:

(iii) (7 + 3x)^-5
సాధన:

(iv) \(\left(4-\frac{x}{3}\right)^{-1 / 2}\)
సాధన:

ప్రశ్న 2.
క్రింది విస్తరణలో సూచించిన పదాలు కనుక్కోండి.
(i) \(\left(1+\frac{x}{2}\right)^{-5}\) లో 6వ పదం
సాధన:

(ii) \(\left(1-\frac{x^2}{3}\right)^{-4}\) విస్తరణలో 7వ పదం
సాధన:

(iii) \((3-4 x)^{-2 / 3}\) విస్తరణలో 10వ పదం
సాధన:

(iv) \(\left(7+\frac{8 y}{3}\right)^{7 / 4}\) విస్తరణలో 5వ పదం
సాధన:

ప్రశ్న 3.
క్రింది విస్తరణలలో మొదటి 3 పదాలు వ్రాయండి.
(i) \((3+5 x)^{-7 / 3}\)
సాధన:

(ii) (1 + 4x)^-4
సాధన:

(iii) \((8-5 x)^{2 / 3}\)
సాధన:

(iv) \((2-7 x)^{-3 / 4}\)
సాధన:

ప్రశ్న 4.
క్రింది విస్తరణలో సాధారణ పదం ((r + 1)వ పదం) కనుక్కోండి.
(i) \((4+5 x)^{-3 / 2}\)
సాధన:

(ii) \(\left(1-\frac{5 x}{3}\right)^{-3}\)
సాధన:

(iii) \(\left(1+\frac{4 x}{5}\right)^{5 / 2}\)
సాధన:

(iv) \(\left(3-\frac{5 x}{4}\right)^{-1 / 2}\)
సాధన:

II.

ప్రశ్న 1.
\(\frac{1+2 x}{(1-2 x)^2}\) విస్తరణలో x10 గుణకం కనుక్కోండి.
సాధన:
\(\frac{1+2 x}{(1-2 x)^2}\) = (1 + 2x) (1 – 2x)^-2
= (1 + 2x) [1 + 2(2x) + 3(2x)² + 4(2x)³ + 5(2x)⁴ + 6(2x)⁵ + 7(2x)⁶ + 8(2x)⁷ + 9(2x)⁸ + 10(2x)⁹ + 11(2x)¹⁰ + …….. + (r + 1) . (2x)^r +……]
∴ \(\frac{1+2 x}{(1-2 x)^2}\) లో x¹⁰ గుణకం = (11) (2)¹⁰ + 10 (2) (2⁹)
= 2¹⁰ (11 + 10)
= 21 × 2¹⁰

ప్రశ్న 2.
\((1-4 x)^{-3 / 5}\) విస్తరణలో x⁴ గుణకం కనుక్కోండి.
సాధన:

ప్రశ్న 3.
(i) \(\frac{(1-3 x)^2}{(3-x)^{3 / 2}}\) విస్తరణలో x⁵ గుణకాన్ని కనుక్కోండి.
సాధన:

(ii) \(\frac{(1+x)^2}{\left(1-\frac{2}{3} x\right)^3}\) విస్తరణలో x⁸ గుణకాన్ని కనుక్కోండి.
సాధన:

(iii) \(\frac{(2+3 x)^3}{(1-3 x)^4}\) విస్తరణలో x⁷ గుణకాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 4.
\(\frac{\left(1+3 x^2\right)^{3 / 2}}{(3+4 x)^{1 / 3}}\) విస్తరణలో x³ గుణకాన్ని కనుక్కోండి.
సాధన:

III.

ప్రశ్న 1.
క్రింది అనంతశ్రేణుల మొత్తాలు కనుక్కోండి.
(i) \(1+\frac{1}{3}+\frac{1.3}{3.6}+\frac{1.3 .5}{3.6 .9}+\ldots \ldots \ldots\)
సాధన:
దత్తశ్రేణి S = \(1+\frac{1}{1} \cdot \frac{1}{3}+\frac{1.3}{1.2}\left(\frac{1}{3}\right)^2+\frac{1.3 \cdot 5}{1.2 .3}\left(\frac{1}{3}\right)^3\) + ……..

(ii) \(1-\frac{4}{5}+\frac{4.7}{5.10}-\frac{4.7 .10}{5.10 .15}+\ldots \ldots\)
సాధన:

(iii) \(\frac{3}{4}+\frac{3.5}{4.8}+\frac{3.5 .7}{4.8 .12}+\ldots\) (Mar. ’11)
సాధన:

(iv) \(\frac{3}{4.8}-\frac{3.5}{4.8 .12}+\frac{3.5 .7}{4.8 .12 .16}-\ldots \ldots\) [T.S. Mar. ’16]
సాధన:

ప్రశ్న 2.
t = \(\frac{4}{5}+\frac{4.6}{5.10}+\frac{4.6 .8}{5.10 .15}+\) …….∞ అయితే, 9t = 16 అని చూపండి.
సాధన:

ప్రశ్న 3.
x = \(\frac{1.3}{3.6}+\frac{1.3 .5}{3.6 .9}+\frac{1.3 .5 .7}{3.6 .9 .12}+\ldots \ldots\) అయితే 9x² + 24x = 11 అని చూపండి. [T.S. Mar. ’16]
సాధన:


3x = 3√3 – 4
⇒ 3x + 4 = 3√3
ఇరువైపుల వర్గం చేయగా
(3x + 4)² = (3√3)²
⇒ 9x² + 24x + 16 = 27
⇒ 9x² + 24x = 11

ప్రశ్న 4.
x = \(\frac{5}{(2 !) \cdot 3}+\frac{5.7}{(3 !) \cdot 3^2}+\frac{5 \cdot 7 \cdot 9}{(4 !) \cdot 3^3}+\ldots\) అయితే x² + 4x విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 5.
క్రింది అనంత శ్రేణి మొత్తం కనుక్కోండి. [A.P. Mar. ’16, Mar. ’05]
\(\frac{7}{5}\left(1+\frac{1}{10^2}+\frac{1.3}{1.2} \cdot \frac{1}{10^4}+\frac{1.3 .5}{1.2 .3} \cdot \frac{1}{10^6}+\ldots\right)\)
సాధన:

ప్రశ్న 6.
x ఒక శూన్యేతర అకరణీయ సంఖ్య అయితే \(1+\frac{x}{2}+\frac{x(x-1)}{2.4}+\frac{x(x-1)(x-2)}{2.4 .6}+\ldots \ldots\) \(=1+\frac{x}{3}+\frac{x(x+1)}{3.6}+\frac{x(x+1)(x+2)}{3.6 .9}+\ldots\) అని నిరూపించండి.
సాధన:

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(a)

అభ్యాసం – 6(ఎ)

I.

ప్రశ్న 1.
ద్విపద సిద్ధాంతాన్ని ఉపయోగించి క్రింది సమాసాలను విస్తరించి వ్రాయండి.
(i) (4x + 5y)⁷
సాధన:

(ii) \(\left(\frac{2}{3} x+\frac{7}{4} y\right)^5\)
సాధన:

(iii) \(\left(\frac{2 p}{5}-\frac{3 q}{7}\right)^6\)
సాధన:

(iv) (3 + x – x²)⁴
సాధన:

ప్రశ్న 2.
క్రింది పదాలు వ్రాసి సూక్ష్మీకరించండి.
(i) \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\) లో 6వ పదం [May ’13]
సాధన:

(ii) (3x – 4y)¹⁰ లో 7వ పదం
సాధన:

(iii) \(\left(\frac{3 p}{4}-5 q\right)^{14}\) లో 10వ పదం
సాధన:

(iv) \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\) లో rవ పదం (1 ≤ r ≤ 9)
సాధన:

ప్రశ్న 3.
క్రింది సమాసాల ద్విపద విస్తరణలలో పదాల సంఖ్యను కనుక్కోండి.
(i) \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\)
సాధన:
(x + a)ⁿ విస్తరణలో n పదాల సంఖ్య = (n + 1)
∴ \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\) ద్విపద విస్తరణలో పదాల సంఖ్య = 9 + 1 = 10

(ii) (3p + 4q)¹⁴
సాధన:
(3p + 4q)¹⁴ ద్విపద విస్తరణలో పదాల సంఖ్య = 14 + 1 = 15

(iii) (2x + 3y + z)⁷ [Mar. ’07; Mar. ’14, ’13]
సాధన:
(a + b + c)ⁿ విస్తరణలో పదాల సంఖ్య = \(\frac{(n+1)(n+2)}{2}\)
n ధన పూర్ణాంకం కనుక
(2x + 3y + z)⁷ లో పదాల సంఖ్య = \(\frac{(7+1)(7+2)}{2}\)
= \(\frac{8 \times 9}{2}\)
= 36

ప్రశ్న 4.
(4x – 7y)⁴⁹ + (4x + 7y)⁴⁹ విస్తరణలో శూన్యేతర గుణకాలు కలిగిన పదాలు ఎన్ని?
సాధన:

ప్రశ్న 5.
(1 + x)³⁹ విస్తరణలో చివరి 20 గుణకాల మొత్తం కనుక్కోండి.
సాధన:

ప్రశ్న 6.
(1 + x)²ⁿ, (1 + x)^2n-1 విస్తరణలలో A, B లు వరుసగా xn గుణకాలు అయితే \(\frac{A}{B}\) విలువ కనుక్కోండి.
సాధన:
ఇచ్చిన దత్తాంశం ప్రకారం (1 + x)²ⁿ మరియు (1 + x)^2n-1 విస్తరణలో xⁿ గుణకాలు A మరియు B అనుకొందాం.
∴ A = ²ⁿC_n
B = ^2n-1C_n

II.

ప్రశ్న 1.
క్రింది గుణకాలను కనుక్కోండి.
(i) \(\left(3 x-\frac{4}{x}\right)^{10}\) లో x^-6 గుణకం
సాధన:

(ii) \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\) లో x¹¹ గుణకం
సాధన:

(iii) \(\left(7 x^3-\frac{2}{x^2}\right)^9\) లో x² గుణకం
సాధన:

(iv) \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)^7\) లో x^-7 గుణకం
సాధన:

ప్రశ్న 2.
క్రింది సమాసాల ద్విపద విస్తరణలలో x లేని పదం (స్థిర పదం) కనుక్కోండి.
(i) \(\left(\frac{\sqrt{x}}{3}-\frac{4}{x^2}\right)^{10}\)
సాధన:

(ii) \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\)
సాధన:

(iii) \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\)
సాధన:

(iv) \(\left(\frac{2 x^2}{5}+\frac{15}{4 x}\right)^9\)
సాధన:

ప్రశ్న 3.
క్రింది సమాసాల ద్విపద విస్తరణలలో మధ్యపదం (పదాలు) కనుక్కోండి.
(i) \(\left(\frac{3 x}{7}-2 y\right)^{10}\)
సాధన:
(x + a)ⁿ విస్తరణలో n సరిసంఖ్య అయిన మధ్యపదం \(T_{\left(\frac{n+1}{2}\right)}\), n బేసిసంఖ్య అయిన రెండు పదాలు \(\frac{T_{n+1}}{2}\), \(\frac{T_{n+3}}{2}\) మధ్యపదాలు అవుతాయి.

(ii) \(\left(4 a+\frac{3}{2} b\right)^{11}\)
సాధన:

(iii) (4x² + 5x³)¹⁷
సాధన:

(iv) \(\left(\frac{3}{a^3}+5 a^4\right)^{20}\)
సాధన:

ప్రశ్న 4.
క్రింది సమాసాల ద్విపద విస్తరణలలో సంఖ్యాపరంగా గరిష్ఠ పదం (పదాలు) కనుక్కోండి.
(i) (4 + 3x)¹⁵, x = \(\frac{7}{2}\)
సాధన:

(ii) (3x + 5y)¹², x = \(\frac{1}{2}\), y = \(\frac{4}{3}\)
సాధన:

(iii) (4a – 6b)¹³, a = 3, b = 5
సాధన:

(iv) (3 + 7x)ⁿ, x = \(\frac{4}{5}\), n = 15
సాధన:
(3 + 7x)ⁿ = \(\left[3\left(1+\frac{7}{3} x\right)\right]^n\)

ప్రశ్న 5.
క్రింది వాటిని నిరూపించండి.
(i) 2.C₀ + 5.C₁ + 8.C₂ + ….. + (3n+2).C_n = (3n + 4) . 2^n-1
సాధన:

(ii) n ఒక సరిధన పూర్ణంకమైతే C₀ – 4 . C₁ + 7 . C₂ – 10 . C₃ + …… = 0
సాధన:

(iii) \(\frac{C_1}{2}+\frac{C_3}{4}+\frac{C_5}{6}+\frac{C_7}{8}+\ldots \ldots=\frac{2^n-1}{n+1}\)
సాధన:

(iv) \(C_0+\frac{3}{2} \cdot C_1+\frac{9}{3} \cdot C_2+\frac{27}{4} \cdot C_3+\ldots \ldots\) \(+\frac{3^n}{n+1} \cdot C_n=\frac{4^{n+1}-1}{3(n+1)}\)
సాధన:

(v) C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ….. + 2ⁿ . C_n = 3ⁿ [May ’07]
సాధన:

ప్రశ్న 6.
క్రింది మొత్తాలను కనుక్కోండి.
(i) \(\frac{{ }^{15} C_1}{{ }^{15} C_0}+2 \cdot \frac{{ }^{15} C_2}{{ }^{15} C_1}+3 \cdot \frac{{ }^{15} C_3}{{ }^{15} C_2}+\ldots \ldots\) \(+15 \cdot \frac{{ }^{15} C_{15}}{{ }^{15} C_{14}}\)
సాధన:

(ii) C₀ . C₃ + C₁ . C₄ + C₂ . C₅ + ….. + C_n-3 . C_n
సాధన:

(iii) 2² . C₀ + 3² . C₁ + 4² . C₂ + …… + (n+2)² . C_n
సాధన:

(iv) 3C₀ + 6C₁ + 12C₂ + …… + 3 . 2ⁿ . C_n
సాధన:

ప్రశ్న 7.
ద్విపద సిద్ధాంతాన్ని ఉపయోగించి ప్రతి ధన పూర్ణాంకం nకు 50ⁿ – 49n – 1 ను 49² భాగిస్తుందని చూపండి.
సాధన:

ప్రశ్న 8.
ద్విపద సిద్ధాంతాన్ని ఉపయోగించి ప్రతి ధన పూర్ణాంకం nకు 5⁴ⁿ + 52n – 1 ను 676 భాగిస్తుందని చూపండి.
సాధన:

ప్రశ్న 9.
(1 + x + x²)ⁿ = a₀ + a₁x + a₂x² + …… + a_2n x²ⁿ, అయితే
(i) a₀ + a₁ + a₂ + ……. + a_2n = 3ⁿ
(ii) a₀ + a₂ + a₄ + …… + a_2n = \(\frac{3^n+1}{2}\)
(iii) a₁ + a₃ + a₅ + …….. + a_2n-1 = \(\frac{3^n-1}{2}\)
(iv) a₀ + a₃ + a₆ + a₉ + …… = 3^n-1 అని చూపండి.
సాధన:

ప్రశ్న 10.
(1 + x + x² + x³)⁷ = b₀ + b₁x + b₂x² + ……. + b₂₁ x²¹ అయితే
(i) b₀ + b₂ + b₄ + …… + b₂₀
(ii) b₁ + b₃ + b₅ + ….. + b₂₁ విలువలు కనుక్కోండి.
సాధన:

ప్రశ్న 11.
\(\left(2+\frac{8 x}{3}\right)^n\) విస్తరణలో x¹¹, x¹² గుణకాలు సమానమైతే n విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 12.
2²⁰¹³ ను 17 తో భాగించగా వచ్చే శేషాన్ని కనుక్కోండి.
సాధన:
2⁴ = 16
2⁴ ను 17 తో భాగించగా వచ్చే శేషం – 1
2²⁰¹³ = (2⁴)⁵⁰³ . 2¹
∴ 2²⁰¹³ ను 17 తో భాగించగా వచ్చే శేషం (-1)⁵⁰³ . 2
= (-1) . 2
= -2

ప్రశ్న 13.
(1 + x)²¹ ద్విపద విస్తరణలో (2r + 4), (3r + 4) పదాల గుణకాలు సమానమయితే విలువ కనుక్కోండి.
సాధన:

III.

ప్రశ్న 1.
(1 + x)ⁿ విస్తరణలో x⁹, x¹⁰, x¹¹ పదాల గుణకాలు అంకశ్రేఢిలో ఉంటే, n² – 41n + 398 = 0 అని చూపండి.
సాధన:

ప్రశ్న 2.
(1 + x)ⁿ విస్తరణలో 3 వరస గుణకాలు 36, 84, 126 అయితే n విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 3.
(a + x)ⁿ విస్తరణలో 2, 3, 4 పదాల గుణకాలు వరుసగా 40, 70, 1080 అయితే a, x, n విలువలు కనుక్కోండి. [T.S. Mar ’16, May ’06]
సాధన:

ప్రశ్న 4.
(1 + x)ⁿ విస్తరణలో r, (r + 1), (r + 2) పదాల గుణకాలు అంకశ్రేఢిలో ఉంటే n² – (4r + 1)n + 4r² – 2 = 0 అని చూపండి.
సాధన:

ప్రశ్న 5.
\(\left(2 x^3-\frac{3}{x^2}\right)^{14}\) విస్తరణలో x³², x^-18 గుణకాల మొత్తం కనుక్కోండి.
సాధన:

ప్రశ్న 6.
(x + a)ⁿ ద్విపద విస్తరణలో బేసిపదాల మొత్తం P, సరిపదాల మొత్తం Q అయితే (i) P² – Q² = (x² – a²)ⁿ (ii) 4PQ = (x + a)²ⁿ – (x – a)²ⁿ అని నిరూపించండి. [A.P. Mar. ’16]
సాధన:

ప్రశ్న 7.
(1 + x)ⁿ ద్విపద విస్తరణలో 4 వరుస పదాల గుణకాలు వరుసగా a₁, a₂, a₃, a₄ అయితే \(\frac{a_1}{a_1+a_2}+\frac{a_3}{a_3+a_4}=\frac{2 a_2}{a_2+a_3}\) అని చూపండి. [Mar. ’11; May ’07]
సాధన:

ప్రశ్న 8.
\(\left({ }^{2 n} C_0\right)^2-\left({ }^{2 n} C_1\right)^2+\left({ }^{2 n} C_2\right)^2-\left({ }^{2 n} C_3\right)^2+\) ……. \(+\left({ }^{2 n} C_{2 n}\right)^2=(-1)^{22 n} C_n\) అని నిరూపించండి.
సాధన:

ప్రశ్న 9.
(C₀ + C₁) (C₁ + C₂) (C₂ + C₃) …. (C_n-1 + C_n) = \(\frac{(n+1)^n}{n !}\) · C₀ . C₁ . C₂ …… C_n అని నిరూపించండి.
సాధన:

ప్రశ్న 10.
\((1+3 x)^n\left(1+\frac{1}{3 x}\right)^n\) విస్తరణలో x లేని పదం (స్థిర పదం) కనుక్కోండి.
సాధన:

ప్రశ్న 11.
(1 + x)²ⁿ ద్విపద విస్తరణలోని మధ్యపదం \(\frac{1.3 .5 \ldots \ldots(2 n-1)}{n !}(2 x)^n\) అనిచూపండి. [May ’06]
సాధన:

ప్రశ్న 12.
(1 + 3x – 2x²)¹⁰ = a₀ + a₁x + a₂x² + …. + a₂₀x²⁰ అయితే
(i) a₀ + a₁ + a₂ + …… + a₂₀ = 2¹⁰
(ii) a₀ – a₁ + a₂ – a₃ + ……… + a₂₀ = 4¹⁰ అని నిరూపించండి.
సాధన:

ప్రశ్న 13.
(3√3 + 5)²ⁿ⁺¹ = x, f = x – [x] అయితే (ఇక్కడ [x] అనేది x పూర్ణాంక భాగాన్ని సూచిస్తుంది.), x . f విలువ కనుక్కోండి.
సాధన:
(3√3 + 5)²ⁿ⁺¹ = x
f = x – [x] ⇒ 0 < f < 1
F = (3√3 – 5)²ⁿ⁺¹ అనుకోండి.
5 < 3√3 < 6
⇒ 0 < 3√3 – 5 < 1
⇒ 0 < (3√3 – 5)²ⁿ⁺¹ < 1
⇒ 0 < F < 1
⇒ 0 > -F > -1
⇒ -1 < -F < 0

ప్రశ్న 14.
R, n లు ధన పూర్ణాంకాలు, n బేసి పూర్ణాంకం, 0 < F < 1, (5√5 + 11)ⁿ = R + F అయితే
(i) R ఒక సరి పూర్ణాంకం
(ii) (R + F) . F = 4ⁿ అని చూపండి.
సాధన:
(i) R, n లు ధన పూర్ణాంకాలు
0 < F < 1, (5√5 + 11)ⁿ = R + F
(5√5 – 11)ⁿ = f అనుకోండి.
121 < 125 < 144 కనుక
ఇప్పుడు 11 < 5√5 < 12
⇒ 0 < 5√5 – 11 < 1
⇒ 0 < (5√5 – 11)ⁿ < 1
⇒ 0 < f < 1
⇒ 0 > -f > -1
∴ -1 < -f < 0
R + F – f = (5√5 + 11)ⁿ – (5√5 – 11)ⁿ
= \(\left[{ }^n C_0(5 \sqrt{5})^n+{ }^n C_1(5 \sqrt{5})^{n-1}(11)\right.\)

ప్రశ్న 15.
I, n లు ధన పూర్ణాంకాలు 0 < f < 1, (7 + 4√3)ⁿ = I + f అయితే
(i) I ఒక బేసి పూర్ణాంకం
(ii) (I + f) (I – f) = 1 అని చూపండి.
సాధన:
I, n లు ధన పూర్ణాంకాలు
(7 + 4√3)ⁿ = I + f, 0 < f < 1
7 – 4√3 = F అనుకోండి.
∴ 36 < 48 < 49
ఇప్పుడు 6 < 4√3 < 7
⇒ -6 > 4√3 > -7
⇒ -7< -4√3 < -6
⇒ 0 < (7 – 4√3)ⁿ < 1
∴ 0 < F < 1
I + f + F = (7 + 4√3)ⁿ + (7 – 4√3)ⁿ

= \(2\left[{ }^n C_0 7^n+{ }^n C_2 7^{n-2}(4 \sqrt{3})^2+\ldots . .\right]\)
= 2k, k పూర్ణాంకం
∴ I + f + F సరిపూర్ణాంకం.
⇒ f + F పూర్ణాంకం, (I పూర్ణాంకం కనుక)
కానీ 0 < f < 1, 0 < F < 1
⇒ 0 < f + F < 2
∴ f + F = 1 …….(1)
⇒ I + 1 సరి పూర్ణాంకం.
∴ I బేసి పూర్ణాంకం.
(I + f) (I – f) = (I + f) F, (1) నుండి
= (7 + 4√3)ⁿ (7 – 4√3)ⁿ
= [(7 + 4√3) (7 – 4√3)]ⁿ
= (49 – 48)ⁿ
= 1

ప్రశ్న 16.
n ధన పూర్ణాంకం అయితే \(\sum_{r=1}^n r^3\left(\frac{{ }^n C_r}{{ }^n C_{r-1}}\right)^2=\frac{(n)(n+1)^2(n+2)}{12}\) అని నిరూపించండి.
సాధన:

ప్రశ్న 17.
\(\left(5^{1 / 6}+2^{1 / 8}\right)^{100}\) విస్తరణలో కరణీయ పదాల సంఖ్యను కనుకోండి.
సాధన:
సాధారణ పదం
\(T_{r+1}={ }^{100} C_r\left(5^{1 / 6}\right)^{100-r}\left(2^{1 / 8}\right)^r\) = \({ }^{100} C_r 5^{\frac{100-r}{6}} \cdot 2^{\frac{r}{8}}\)
0 ≤ r ≤ 100 లో r = 4, 10, 16, 22, 28, 34, 40, 46, 52, 58, 64, 70, 76, 82, 88, 94, 100 అయితే \(\frac{100-r}{6}\) ఒక పూర్ణాంకం
0 ≤ r ≤ 100 లో r = 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96\(\frac{r}{8}\) ఒక పూర్ణాంకం
0 ≤ r ≤ 100 అయితే r = 16, 40, 64, 88 అయితే \(\frac{100-r}{6}, \frac{r}{8}\) లు రెండూ పూర్ణాంకాలు
∴ \(\left(5^{1 / 6}+2^{1 / 8}\right)^r\) విస్తరణలో అకరణీయ పదాలు = 4
∴ \(\left(5^{1 / 6}+2^{1 / 8}\right)^r\) విస్తరణలో కరణీయ పదాల సంఖ్య = 101 – 4 = 97

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(e) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(e)

అభ్యాసం – 5(ఇ)

I.

ప్రశ్న 1.
ⁿC₄ = 210, అయితే n విలువ ఎంత?
సాధన:
సూచన: ⁿC_r = \(\frac{n !}{(n-r) ! r !}\) = \(\frac{n \cdot(n-1)(n-2) \ldots \ldots / n-(r-1)]}{1.2 .3 \ldots \ldots \ldots . .}\)
ⁿC₄ = 210
⇒ \(\frac{n(n-1)(n-2)(n-3)}{1.2 .3 .4}\) = 10 × 21
⇒ n(n – 1) (n – 2) (n – 3) = 10 × 21 × 1 × 2 × 3 × 4
⇒ n(n – 1) (n – 2) (n – 3) = 10 × 7 × 3 × 2 × 3 × 4
⇒ n(n – 1) (n – 2) (n – 3) = 10 × 9 × 8 × 7
∴ n = 10

ప్రశ్న 2.
¹²C_r = 495, అయితే r విలువ కనుక్కోండి.
సాధన:
సూచన: ⁿC_r = ⁿC_n-r
¹²C_r = 495
= 5 × 99
= 11 × 9 × 5
= \(\frac{12 \times 11 \times 9 \times 5 \times 2}{12 \times 2}\)
= \(\frac{12 \times 11 \times 10 \times 9}{1.2 .3 .4}\)
= ¹²C₄ లేదా ¹²C₈
∴ r = 4 లేదా 8

ప్రశ్న 3.
10 . ⁿC₂ = 3 . ⁿ⁺¹C₃, అయితే n విలువ ఎంత?
సాధన:
10 . ⁿC₂ = 3 . ⁿ⁺¹C₃
⇒ 10 × \(\frac{n(n-1)}{1.2}=\frac{3(n+1) n(n-1)}{1.2 .3}\)
⇒ 10 = n + 1
⇒ n = 9

ప్రశ్న 4.
ⁿP_r = 5040, ⁿC_r = 210 అయితే n, r విలువలను కనుక్కోండి. [A.P. Mar. ’16]
సాధన:
సూచన: ⁿP_r = r! ⁿC_r మరియు ⁿP_r = n(n – 1) (n – 2)…. [n – (r – 1)]
ⁿP_r = 5040, ⁿC_r = 210
r! = \(\frac{{ }^n P_r}{{ }^n C_r}=\frac{5040}{210}=\frac{504}{21}\) = 24 = 4!
∴ r = 4
ⁿP_r = 5040
ⁿP₄ = 5040
= 10 × 504
= 10 × 9 × 56
= 10 × 9 × 8 × 7
= ¹⁰P₄
∴ n = 10
∴ n = 10, r = 4

ప్రశ్న 5.
ⁿC₄ = ⁿC₆, అయితే n ఎంత?
సాధన:
సూచన: ⁿC_r = ⁿC_s ⇒ r = s or r + s = n
ⁿC₄ = ⁿC₆
∴ n = 4 + 6 = 10

ప్రశ్న 6.
¹⁵C_2r-1 = ¹⁵C_2r+4 అయితే r విలువ కనుక్కోండి. [Mar. ’14, ’05]
సాధన:
¹⁵C_2r-1 = ¹⁵C_2r+4
⇒ 2r – 1 = 2r + 4 లేదా (2r – 1) + (2r + 4) = 15
⇒ 4r + 3 = 15
⇒ 4r = 12
⇒ r = 3
∴ 2r – 1 = 2r + 4
⇒ -1 = 4 ఇది అసాధ్యం
∴ r = 3

ప్రశ్న 7.
¹⁷C_2t+1 = ¹⁷C_3t-5, అయితే t విలువ ఎంత?
సాధన:
¹⁷C_2t+1 = ¹⁷C_3t-5
⇒ 2t + 1 = 3t – 5 లేదా (2t + 1) + (3t – 5) = 17
⇒ 1 + 5 = t లేదా 5t = 21
⇒ t = 6 లేదా t = \(\frac{21}{5}\) ఇది పూర్ణాంకము కాదు
∴ t = 6

ప్రశ్న 8.
¹²C_r+1 = ¹²C_3r-5, అయితే r విలువ కనుక్కోండి. [T.S. Mar. ’16, Mar. ’08]
సాధన:
¹²C_r+1 = ¹²C_3r-5
⇒ r + 1 = 3r – 5 లేదా (r + 1) + (3r – 5) = 12
⇒ 1 + 5 = 2r లేదా 4r – 4 = 12
⇒ 2r = 6 లేదా 4r = 16
⇒ r = 3 లేదా r = 4
∴ r = 3 లేదా 4

ప్రశ్న 9.
⁹C₃ + ⁹C₅ = ¹⁰C_r, అయితే r విలువ కనుక్కోండి?
సాధన:
సూచన: ⁿC_r = ⁿC_n-r
¹⁰C_r = ⁹C₃ + ⁹C₅
∴ ⁿC_r + ⁿC_r-1 = ⁽ⁿ⁺¹⁾C_r
⁹C₆ + ⁹C₅ = ¹⁰C₆ లేదా ¹⁰C₄
∴ r = 4 లేదా 6

ప్రశ్న 10.
ఆరుగురు పురుషులు ముగ్గురు స్త్రీల నుంచి అయిదుగురు సభ్యులున్న కమిటీలు ఎన్ని ఏర్పరచవచ్చు?
సాధన:
వ్యక్తుల సంఖ్య = 6 + 3 = 9
ఈ 9 మంది నుండి 5 గురు సభ్యులున్న కమిటీ ఏర్పరచే విధానాలు = ⁹C₅
= ⁹C₄
= \(\frac{9 \times 8 \times 7 \times 6}{1 \times 2 \times 3 \times 4}\)
= 126

ప్రశ్న 11.
పై ప్రశ్నలో కనీసం ఇద్దరు స్త్రీలు ఉండే కమిటీలు ఎన్ని?
సాధన:
కమిటీలో కనీసం ఇద్దరు స్త్రీలు ఉండేటట్లుగా కమిటీలను ఈక్రింది విధంగా ఎన్నుకోవచ్చు.
(i) ముగ్గురు పురుషులు, ఇద్దరు స్త్రీలు
ముగ్గురు పురుషులు, ఇద్దరు స్త్రీలను ఎన్నుకొనే విధానాల సంఖ్య = ⁶C₃ × ³C₂
= 20 × 3
= 60
(ii) ఇద్దరు పురుషులు, ముగ్గురు స్త్రీలు
ఇద్దరు పురుషులు, ముగ్గురు స్త్రీలను ఎన్నుకొనే విధానాల సంఖ్య = ⁶C₂ × ³C₂
= 15 × 1
= 15
∴ కనీసం ఇద్దరు స్త్రీలు ఉండేటట్లుగా కమిటీలను ఎన్ను కొనే విధానాల సంఖ్య = 60 + 15 = 75

ప్రశ్న 12.
ⁿC₅ = ⁿC₆, అయితే ¹³C_n విలువ ఎంత? [Mar. ’13]
సాధన:
ⁿC₅ = ⁿC₆
⇒ n = 6 + 5 = 11
¹³C_n = ¹³C₁₁
= ¹³C₂
= \(\frac{13 \times 12}{1 \times 2}\)
= 78

II.

ప్రశ్న 1.
3 ≤ r ≤ n కు ^(n-3)C_r + 3 ^(n-3)C_r-1 + 3 ^(n-3)C_r-2 + ^(n-3)C_r-3 = ⁿC_r అని నిరూపించండి.
సాధన:

ప్రశ్న 2.
¹⁰C₅ + 2 . ¹⁰C₄ + ¹⁰C₃ విలువ ఎంత?
సాధన:
సూచన: ⁿC_r + ⁿC_r-1 = ⁽ⁿ⁺¹⁾C_r
¹⁰C₅ + 2 . ¹⁰C₄ + ¹⁰C₃

ప్రశ్న 3.
సూక్ష్మీకరించండి ³⁴C₅ + \(\sum_{r=0}^4(38-r) C_4\)
సాధన:

ప్రశ్న 4.
ఒక తరగతిలో 30 మంది విద్యార్థులున్నారు. వారిలో ప్రతి విద్యార్థి మిగిలిన విద్యార్థులందరితో ఒక చదరంగం ఆటను ఆడితే మొత్తం ఎన్ని చదరంగం ఆటలు వారు ఆడినట్లు?
సాధన:
తరగతిలోని విద్యార్థుల సంఖ్య = 30
ప్రతి విద్యార్థి మిగిలిన విద్యార్థులందరితో ఒక్కో చదరంగం ఆటను ఆడతాడు.
కనుక మొత్తం చదరంగం ఆటల సంఖ్య = ³⁰C₂
= \(\frac{30 \times 29}{1 \times 2}\)
= 435

ప్రశ్న 5.
ఏడుగురు బాలికలు, ఆరుగురు బాలురు నుంచి ముగ్గురు బాలురు, ముగ్గురు బాలికలు ఉండే కమిటీలను ఎన్ని రకాలుగా ఏర్పరచవచ్చు?
సాధన:
ఏడుగురు బాలికలు, ఆరుగురు బాలురు నుండి ముగ్గురు బాలురు, ముగ్గురు బాలికలు ఉండే కమిటీల సంఖ్య = ⁷C₃ × ⁶C₃
= 35 × 20
= 700

ప్రశ్న 6.
10 మంది వ్యక్తుల నుంచి నిర్దేశించిన ఒక వ్యక్తి ఉండేలా ఆరుగురు సభ్యుల కమిటీలు ఎన్ని ఏర్పరచవచ్చు?
సాధన:
నిర్దేశించిన వ్యక్తి కమిటీలో ఉండి, మిగిలిన 9 మంది నుండి 5 గురు వ్యక్తులను ఎన్నుకొనే విధాల సంఖ్య = ⁹C₅
∴ 10 మంది వ్యక్తుల నుంచి నిర్దేశించిన వ్యక్తి ఉండేలా ఆరుగురు సభ్యుల కమిటీలు ఎన్నుకొనే విధాల సంఖ్య = ⁹C₅
= \(\frac{9 \times 8 \times 7 \times 6 \times 5}{1 \times 2 \times 3 \times 4 \times 5}\)
= 126

ప్రశ్న 7.
ఇచ్చిన 9 పుస్తకాల నుంచి నిర్దేశించిన ఒక పుస్తకం లేకుండా 5 పుస్తకాలను ఎన్ని రకాలుగా ఎంచుకోవచ్చు?
సాధన:
9 పుస్తకాలనుంచి నిర్దేశించిన ఒక పుస్తకం లేకుండా 5 పుస్తకాలు ఎన్నుకోవాలి. అంటే నిర్దేశించిన ఆ పుస్తకం తీసివేసి, మిగిలిన 8 పుస్తకాల నుండి 5 పుస్తకాలు ఎంచుకోవాలి. ఈ పనిని 8C5 విధాలుగా చేయవచ్చు.
కనుక కావలసిన సంయోగాల సంఖ్య = ⁸C₅
= ⁸C₃
= \(\frac{8 \times 7 \times 6}{1 \times 2 \times 3}\)
= 56

ప్రశ్న 8.
EQUATION పదంలోని అక్షరాల నుంచి 3 అచ్చులు, 2 హల్లులు ఎన్ని రకాలుగా ఎంచుకోవచ్చు? [May ’11, Mar. ’07]
సాధన:
EQUATION అనే పదంలో {E, U, A, I, O} అను 5 అచ్చుల {Q, T, N} అను 3 హల్లులు కలవు.
అందులో 3 అచ్చులు, 2. హల్లులు ఎన్నుకొనే విధాలు = ⁵C₃ × ³C₂
= 10 × 3
= 30

ప్రశ్న 9.
12 భుజాలున్న ఒక బహుభుజి కర్ణాల సంఖ్య కనుక్కోండి.
సాధన:
ఇచ్చట n = 12
n భుజాలున్న బహుభుజి కర్ణాల సంఖ్య = \(\frac{n(n-3)}{2}\)
= \(\frac{12 \times 9}{2}\)
= 54

ప్రశ్న 10.
ఒక వరుసలో ఉన్న n వ్యక్తుల నుంచి పక్క పక్కనే ఉన్న ఇద్దరు వ్యక్తులను ఎన్ని రకాలుగా ఎంచుకోవచ్చు?
సాధన:
ఒక వరుసలో ఉన్న n వ్యక్తుల నుంచి, పక్కపక్కనే ఉన్న ఇద్దరు వ్యక్తులను ఎంచుకొనే విధాల సంఖ్య = n – 1

ప్రశ్న 11.
4 సరూప నాణేలను 5 గురు బాలురకు ఎవరికైనా ఎన్నైనా ఇచ్చే పద్ధతిలో ఎన్ని రకాలుగా పంచవచ్చు?
సాధన:
4 సరూప నాణేలను ఈ క్రింది విభిన్న సమూహాలుగా విభజించవచ్చు.
(i) ఒక సమూహంలో 4 నాణేలు
(ii) రెండు సమూహాలలో వరుసగా 1, 3 నాణేలు
(iii) రెండు సమూహాలలో వరుసగా 2, 2 నాణేలు
(iv) రెండు సమూహాలలో వరుసగా 3, 1 నాణేలు
(v) మూడు సమూహాలలో వరుసగా 1, 1, 2 నాణేలు
(vi) మూడు సమూహాలలో వరుసగా 1, 2, 1 నాణేలు
(vii) మూడు సమూహాలలో వరుసగా 2, 1, 1 నాణేలు
(viii) నాలుగు సమూహాలలో వరుసగా 1, 1, 1, 1 నాణేలు
ఈ సమూహాలను 5 గురు బాలురకు పంచే విధాల సంఖ్య
= \({ }^5 C_1+2 \times{ }^5 C_2+{ }^5 C_2+{ }^5 C_3 \times \frac{3 !}{2 !}+{ }^5 C_4\)
= 5 + 20 + 10 + 30 + 5
= 70

III.

ప్రశ్న 1.
\(\frac{{ }^{4 n} C_{2 n}}{{ }^{2 n} C_n}=\frac{1.3 .5 \ldots \ldots(4 n-1)}{\{1.3 .5 \ldots \ldots(2 n-1)\}^2}\) అని నిరూపించండి.
సాధన:

ప్రశ్న 2.
ఒక సమితి A లో 12 మూలకాలున్నాయి. ఆ సమితిలో
(i) 4 మూలకాలున్న ఉపసమితులెన్ని?
(ii) కనీసం 3 మూలకాలున్న ఉపసమితులెన్ని?
(iii) 3 లేదా అంతకంటే తక్కువ మూలకాలున్న ఉపసమితులెన్ని? [May ’07]
సాధన:
సమితి A లో వున్న మూలకాల సంఖ్య = 12
(i) 4 మూలకాలున్న ఉపసమితుల సంఖ్య = ¹²C₄
= \(\frac{2 \times 11 \times 10 \times 9}{1 \times 2 \times 3 \times 4}\)
= 495
(ii) కనీసం 3 మూలకాలున్న ఉపసమితులు.
పై లెక్క ప్రకారం కనీసం రెండు మూలకాలున్న ఉపసమితులు = ¹²C₀ + ¹²C₁ + ¹²C₂
= 1 + 12 + 66
= 79
A సమితికున్న మొత్తం ఉపసమితుల సంఖ్య = 2¹²
∴ కనీసం 3 మూలకాలున్న ఉపసమితులు = 2¹² – (79)
= 4096 – 79
= 4017
(iii) 3 లేదా అంతకంటే తక్కువ మూలకాలున్న ఉప సమితులు సున్నా మూలకాలు
(i.e.,) మూలకాలు లేని ఉపసమితిల సంఖ్య = ¹²C₀ = 1
ఒకే ఒక మూలకము వున్న ఉపసమితులు = ¹²C₁ = 12
రెండు మూలకములు వున్న ఉపసమితులు = ¹²C₂
= \(\frac{12 \times 11}{1 \times 2}\)
= 66
మూడు మూలకములు వున్న ఉపసమితులు = ¹²C₃
= \(\frac{12 \times 11 \times 10}{1 \times 2 \times 3}\)
= 220
∴ కనీసం 3 మూలకాలున్న ఉపసమితులు = 1 + 12 + 66 + 220 = 299

ప్రశ్న 3.
ఏడుగురు బాట్స్మెన్, ఆరుగురు బౌలర్లు నుంచి కనీసం అయిదుగురు బౌలర్లు ఉన్న పదకొండు మంది క్రికెట్ టీమును ఎన్ని రకాలుగా ఏర్పరచవచ్చు?
సాధన:
కనీసం 5 గురు బౌలర్లు ఉన్న పదకొండు మంది క్రికెట్ టీమును క్రింద చూపిన విధాలుగా ఎంచుకోవచ్చు.

∴ కోరిన విధంగా క్రికెట్ టీముని ఎంచుకొనే విధానాలు = 42 + 21 = 63

ప్రశ్న 4.
5 అచ్చులు, 6 హల్లులు నుంచి 3 అచ్చులు, 3 హల్లులు ఉండేలా ఎన్ని 6 అక్షరాల పదాలు ఏర్పరచవచ్చు.
సాధన:
అచ్చుల సంఖ్య = 5
హల్లుల సంఖ్య = 6
5 అచ్చుల నుండి 3 అచ్చులు ఎన్నుకొనే విధానాల సంఖ్య = ⁵P₃
6 హల్లులు నుండి 3 హల్లులు ఎన్నుకొనే విధానాల సంఖ్య = ⁶P₃
ఈ 6 అక్షరాలను వాటిలో వాటిని మార్చి వ్రాయగల పదాల సంఖ్య 6!
∴ 6 అక్షరాల పదాలలో 3 అచ్చులు 3 హల్లులు ఉండేలా ఎన్నుకోగల పదాల సంఖ్య = ⁵C₃ × ⁶C₃ × 6!

ప్రశ్న 5.
ఒక రైలు మార్గంలో 8 స్టేషన్లు ఉన్నాయి. వీటిలో 3 స్టేషన్లలో రైలు ఆపాలి. ఆ మూడు స్టేషన్లలో ఏ రెండూ పక్కపక్కన లేకుండా ఎన్ని రకాలుగా ఎంచుకోవచ్చు? [Mar. ’08]
సాధన:
మొదటి రైలు ఆగే స్టేషన్ ముందు గల స్టేషన్ల సంఖ్య x₁ అనుకోండి. ఇట్లే మొదట, రెండు రైలు ఆగే మధ్య x₂ స్టేషన్లు, రెండు, మూడు రైలు ఆగే స్టేషన్ల మధ్య x₃, స్టేషన్లు మరియు మూడవసారి రైలు ఆగిన తరువాత x₄ స్టేషన్లు ఉన్నాయి అనుకోండి.
అప్పుడు x₁ ≥ 0, x₂ ≥ 1, x₃ ≥ 1, x₄ ≥ 0 మరియు x₁ + x₂ + x₃ + x₄ = n – 3
ఈ సమీకరణానికి గల సాధనల సంఖ్య ⁶C₃
∴ ఏ రెండు స్టేషన్లు పక్క పక్కన లేకుండా 8 స్టేషన్లలో 3 స్టేషన్లు ఎంచుకొనే విధానాలు = ⁶C₃
= \(\frac{6 \times 5 \times 4}{1 \times 2 \times 3}\)
= 20

ప్రశ్న 6.
ఆరుగురు భారతీయులు, అయిదుగురు అమెరికా దేశస్థుల నుంచి అయిదుగురు సభ్యులున్న కమిటీని, ఆ కమిటీలో భారతీయుల సంఖ్య పెద్దదిగా ఉండేలా ఎన్ని రకాలుగా ఎంచుకోవచ్చు? [Mar. ’13, ’08]
సాధన:
కమిటీలో భారతీయుల సంఖ్య పెద్దదిగా ఉండేటట్లు కమిటీని ఎన్నుకొనే విధాలు ఈ క్రింద ఇవ్వబడినవి.

∴ కమిటీని కోరిన విధంగా ఎంచుకొనే విధానాల సంఖ్య = 200 + 75 + 6 = 281

ప్రశ్న 7.
ఒక ప్రశ్నాపత్రంలో A, B, C అనే మూడు భాగాలలో వరుసగా 3, 4, 5 ప్రశ్నలున్నాయి. ఒక్కో భాగం నుంచి కనీసం ఒక ప్రశ్న ఉండే విధంగా మొత్తం 6 ప్రశ్నలు ఎన్ని రకాలుగా ఎంచుకోవచ్చు?
సాధన:
మొదటి పద్దతి
ఒక్కొక్క భాగం నుంచి ఒక ప్రశ్న ఉండే విధంగా 6 ప్రశ్నలు ఎన్నుకొనే విధాలు ఈ క్రింది ఇవ్వబడినవి.

రెండవ పద్ధతి
ఒక్కో భాగం నుంచి కనీసం ఒక ప్రశ్న ఉండే విధంగా మొత్తం 6 ప్రశ్నలు ఎంచుకొనే విధాలు = మొత్తం 12 ప్రశ్నల నుండి 6 ప్రశ్నలు ఎంచుకొనే విధాలు – C భాగం నుండి కాక మిగిలిన రెండు భాగాల నుండి 6 ప్రశ్నలు ఎన్నుకోవడం – B నుండి కాక మిగిలిన రెండు భాగాల నుండి 6 ప్రశ్నలు ఎన్నుకోవటం – A నుండి కాక మిగిలిన రెండు భాగాల నుండి 6 ప్రశ్నలు ఎన్నుకోవడం
= ¹²C₆ – ⁷C₆ – ⁸C₆ – ⁹C₆
= 805

ప్రశ్న 8.
12 విభిన్నమైన వస్తువులను ఎన్నిరకాలుగా
(i) 4 సమభాగాలుగా చేయవచ్చు
(ii) నలుగురు వ్యక్తులకు సమానంగా పంచవచ్చు?
సాధన:
(i) 12 విభిన్న వస్తువులను 4 సమభాగాలుగా విభజించే విధానాలు = \(\frac{(12) !}{(3)^4 4 !}\)
(ii) నలుగురు వ్యక్తులకు సమానంగా 12 విభిన్న వస్తువులు పంచే విధాల సంఖ్య = \(\frac{(12) !}{(3 !)^4}\)

ప్రశ్న 9.
ఒక తరగతిలో నలుగురు బాలురు, ఆ బాలికలున్నారు. ప్రతీ ఆదివారం వారిలో కనీసం ముగ్గురు బాలురు ఉండేలా 5 గురు ఉన్న సమూహం విహారయాత్రకు వెళ్తారు. ప్రతీ ఆదివారం వేర్వేరు సమూహాలు విహారయాత్రకు వెళ్తాయి. వారి తరగతి ఉపాధ్యాయిని విహార యాత్రకు వచ్చిన ప్రతీ అమ్మాయికి ప్రతిసారి ఒక్కో బొమ్మ ఇవ్వగా వచ్చే మొత్తం బొమ్మల సంఖ్య 85 ఐతే g విలువ కనుక్కోండి.
సాధన:
బాలుర సంఖ్య = 4
బాలికల సంఖ్య = g
కనీసం ముగ్గురు బాలురు ఉండేలా ఈ క్రింది పట్టికలో తెలిపిన విధంగా ఎన్నుకొనవచ్చును.

G₁ లో బాలికల సంఖ్య = [⁴C₃ × ⁹C₂] × 2 ఎందువలననగా ప్రతిసారి ఇద్దరు బాలికలు ఉంటారు.
G₂ లో బాలికల సంఖ్య = [⁴C₃ × ⁹C2] × 1 ఎందువలననగా ప్రతిసారి ఒక బాలిక ఉంటుంది.
మొత్తం బాలికలకు ఇచ్చిన బొమ్మల సంఖ్య = 85
⇒ [⁴C₃ × ⁹C₂] × 2 + [⁴C₃ × ⁹C₂] × 1 = 85
⇒ 4 . \(\frac{g(g-1)}{2}\) × 2 + 1 . g . 1 = 85
⇒ 4g² – 4g + g – 85 = 0
⇒ 4g² – 3g – 85 = 0
⇒ 4g² – 20g + 17g – 85 = 0
⇒ 4g(g – 5) + 17(g – 5) = 0
⇒ (g – 5) (4g + 17) = 0
g ≠ \(\frac{17}{5}\) కనుక
∴ g = 5
∴ బాలికల సంఖ్య = 5

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(d) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(d)

అభ్యాసం – 5(డి)

I.

ప్రశ్న 1.
కింది పదాలలోని అక్షరాలను అమర్చడం ద్వారా వచ్చే ప్రస్తారాల సంఖ్యను కనుక్కోండి. (May ’13, Mar. ’11, ’06)
(i) INDEPENDENCE
(ii) MATHEMATICS
(iii) SINGING
(iv) PERMUTATION
(v) COMBINATION
(vi) INTERMEDIATE
సాధన:
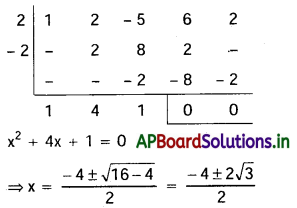
(i) INDEPENDENCE పదంలో 12 అక్షరాలున్నవి. అందులో 3N లు, 2D లు, 4E లు మిగిలినవి విభిన్నాలు.
కనుక వాటిని అమర్చడం ద్వారా వచ్చే ప్రస్తారాల సంఖ్య = \(\frac{(12) !}{3 ! 2 ! 4 !}\)

(ii) MATHEMATICS అనే పదంలో 11 అక్షరాలున్నవి. అందులో 2M లు, 2A లు, 2T లు మిగిలినవి విభిన్నాలు.
కనుక వాటిని అమర్చడం ద్వారా వచ్చే ప్రస్తారాల సంఖ్య = \(\frac{(11) !}{2 ! 2 ! 2 !}\)

(iii) SINGING అనే పదంలో 7 అక్షరాలున్నవి. అందులో 2I లు, 2N లు, 2G లు
కనుక వాటిని అమర్చడం ద్వారా వచ్చే ప్రస్తారాల సంఖ్య = \(\frac{7 !}{2 ! 2 ! 2 !}\)

(iv) PERMUTATION అనే పదంలో 11 అక్షరాలున్నవి. అందు 2T లు మిగిలినవి విభిన్నాలు.
కనుక వాటిని అమర్చడం ద్వారా వచ్చే ప్రస్తారాల సంఖ్య = \(\frac{(11) !}{2 !}\)

(v) COMBINATION అనే పదంలో 11 అక్షరాలున్నవి. అందు 2 ‘O’లు 2 ‘I’ లు, 2N లు మిగిలినవి విభిన్నాలు,
కనుక వాటిని అమర్చడం ద్వారా వచ్చే ప్రస్తారాల సంఖ్య = \(\frac{(11) !}{2 ! 2 ! 2 !}\)

(vi) INTERMEDIATE పదంలో 12 అక్షరాలున్నవి. అందు 2I లు 2T లు 3E లు మిగిలినవి విభిన్నాలు.
కనుక వాటిని అమర్చడం ద్వారా వచ్చే ప్రస్తారాల సంఖ్య = \(\frac{(12) !}{2 ! 2 ! 3 !}\)

ప్రశ్న 2.
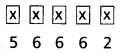
2, 2, 2, 3, 3, 4, 4 అంకెలతో ఏర్పరచగల 7 అంకెల సంఖ్యలెన్ని?
సాధన:
ఇచ్చిన 7 అంకెలలో 2 మూడుసార్లు, 3 రెండుసార్లు, 4లు రెండు సార్లు పునరావృతం అయ్యాయి.
కనుక ఈ 7 అంకెలతో ఏర్పడే 7 అంకెల సంఖ్యలు = \(\frac{7 !}{3 ! 2 ! 2 !}\)

II.

ప్రశ్న 1.
RAMANA పదంలోని అక్షరాలనుపయోగించి ఎన్ని 4 అక్షరాలు పదాలు తయారుచేయవచ్చు?
సాధన:
RAMANA పదంలో 3A లు, 3 విభిన్న (R, M, N) అక్షరాలున్నవి.
6 అక్షరాలనుండి 4 అక్షరాలున్న పదాలను ఈ క్రింది విధంగా తయారు చేయవచ్చు.
Case (i): అన్ని విభిన్న అక్షరాలు (i.e.,) R, A, M, N
4 అక్షరాల పదాల సంఖ్య = 4! = 24

Case (ii): 2A లు, మిగిలిన రెండు R, M, N ల నుండి ఏవైనా రెండు అక్షరాలు అంటే 3 విభిన్న అక్షరాల నుండి రెండింటిని ఎన్నుకొనే విధాల సంఖ్య = ³C₂
4 అక్షరాల పదాల సంఖ్య = ³C₂ × \(\frac{4 !}{2 !}\)
= 3 × \(\frac{24}{2}\)
= 36

Case (iii): 3Aలు, మిగిలిన ఒక అక్షరం R, M, N లలో ఏదో ఒకటి అంటే 3 విభిన్న అక్షరాల నుండి ఒక అక్షరాన్ని ఎన్నుకొనే విధాల సంఖ్య = ³C₁ = 3
4 అక్షరాలతో ఏర్పడే పదాల సంఖ్య = 3 × \(\frac{4 !}{3 !}\)
= 3 × \(\frac{24}{6}\)
= 12
∴ RAMANA అనే పదంలోని అక్షరాలనుపయోగించిన ఏర్పడే 4 అక్షరాలున్న పదాల సంఖ్య = 24 + 36 + 12 = 72

ప్రశ్న 2.
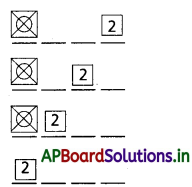
1, 2, 3, 4, 3, 2, 1 అంకెలనుపయోగించి, సరిస్థానాల్లో సరి అంకెలు మాత్రమే ఉండేటట్లు ఎన్ని 7 అంకెల సంఖ్యలు తయారు చేయవచ్చు?
సాధన:

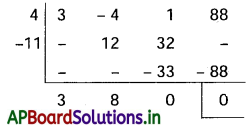
2, 4, 6 స్థానాలు సరిస్థానాలు, ఇచ్చిన 7 అంకెలలో 1 రెండుసార్లు, 2 రెండుసార్లు, 3 రెండుసార్లు, 4 ఒకసారి వచ్చినవి.
3 సరిస్థానాల్లో 2, 2, 4 లను అమర్చే విధాల సంఖ్య = \(\frac{3 !}{2 !}\)
= \(\frac{6}{2}\)
= 3
మిగిలిన 4 స్థానాలల్లో 1, 1, 3, 3 లను అమర్చే విధాల సంఖ్య = \(\frac{4 !}{21.2 !}=\frac{24}{2 \times 2}\) = 6
∴ ప్రస్తారాల సంఖ్య = 3 × 6 = 18

ప్రశ్న 3.
ఒక గ్రంథాలయంలో ఒక పుస్తకానికి 6 ప్రతులు, మరొక రెండు విభిన్నమైన పుస్తకాలకు ఒక్కోదానికి 4 ప్రతులు, వేరొక మూడు విభిన్నమైన పుస్తకాలకు ఒక్కొదానికి 5 ప్రతులు ఇంకో రెండు విభిన్న పుస్తకాలు ఒక్కొక్క దానికి 3 ప్రతులు ఉన్నాయి. ఈ పుస్తకాలన్నింటినీ ఒక వరసలో ఎన్ని విధాలుగా అమర్చవచ్చు?
సాధన:
గ్రంథాలయంలోని పుస్తకాల సంఖ్య = 6 + (4 × 2) + (3 × 5) + (2 × 3) = 35
పుస్తకాలన్నింటిని ఒక వరసలో అమర్చే విధాల సంఖ్య = \(\frac{(35) !}{6 !(4 !)^2(5 !)^3(3 !)^2}\)

ప్రశ్న 4.
ఒక పుస్తక భాండాగారంలో ‘n’ విభిన్న పుస్తకాలు ఒక్కొక్కటి ‘m’ ప్రతులున్నాయి. ఈ పుస్తకాలన్నింటినీ ఒక వరసలో ఎన్నివిధాలుగా అమర్చవచ్చు?
సాధన:
పుస్తక భాండాగారంలో పుస్తకాల సంఖ్య = m × n = mn
∴ పుస్తకాలన్నింటిని ఒక వరుసలో అమర్చే విధాల సంఖ్య = \(\frac{(m n) !}{(m !)^n}\)

ప్రశ్న 5.
0, 1, 1, 2, 3 అంకెలన్నింటినీ ఉపయోగించి ఏర్పరచగల 5 అంకెల సంఖ్య లెన్ని?
సాధన:
0, 1, 1, 2, 3 అంకెలన్నింటినీ ఉపయోగిస్తే ఏర్పడే 5 అంకెల సంఖ్యలు = \(\frac{5 !}{2 !}\) = 60
కాని అందుకొన్ని సంఖ్యలు ‘0’ తో మొదలవుతాయి. అవి నాలుగు అంకెల సంఖ్యలు మాత్రమే అవుతాయి.
అటువంటివి = \(\frac{4 !}{2 !}=\frac{24}{2}\) = 12
కనుక 0, 1, 1, 2, 3 అంకెలతో ఏర్పడే 5 అంకెల సంఖ్యలు = 60 – 12 = 48

ప్రశ్న 6.
CHEESE పదంలోని అక్షరాలను ఏ రెండు E లు పక్క పక్కన రాకుండా ఎన్ని రకాలుగా అమర్చవచ్చు?
సాధన:
CHEESE పదంలో 6 అక్షరాలున్నవి. అందు 3E లు మిగిలినవి విభిన్నాలు. 3E లలో ఏ రెండు పక్క పక్కన రాకూడదు.
కనుక మిగిలిన 3 అక్షరాలను ఒక వరుసలో 3! విధాలుగా అమర్చవచ్చు.
ఆ తరువాత వాటి మధ్యలో మొదట, చివర కలిపి 4 ఖాళీలుంటాయి.
ఈ 4 ఖాళీలలో 3E లను \(\frac{{ }^4 P_3}{3 !}=\frac{4 !}{3 !}\) = 4 విధాలుగా అమర్చవచ్చు.
కనుక కావలసిన ప్రస్తారాల సంఖ్య = (3!) × 4
= 6 × 4
= 24

III.

ప్రశ్న 1.
ASSOCIATIONS పదంలోని అక్షరాలను ఎన్ని రకాలుగా అమర్చవచ్చు?
ఈ అమరికలలో ఎన్నింటిలో
(i) అన్ని ‘S’ లు కలిసి వుంటాయి?
(ii) రెండు ‘A’ లు విడివిడిగా ఉంటాయి?
సాధన:
ASSOCIATIONS అనే పదంలో 12 అక్షరాలున్నాయి.
వీటిలో రెండు A లు, మూడు S లు, రెండు O లు, రెండు I లు, మిగిలినవి విభిన్న అక్షరాలున్నాయి.
ఈ 12 అక్షరాలను అమర్చడం ద్వారా వచ్చే ప్రస్తారాల సంఖ్య = \(\frac{(12) !}{2 ! 3 ! 2 ! 2 !}\)
సూచన: n వస్తువులలో p ఒక రకానికి చెందినవి. q రెండవ రకానికి చెందిన, r వేరొక రకానికి చెందిన వస్తువులై మిగిలినవి విభిన్నాలు అయిన n వస్తువులలో ఏర్పడే
ప్రస్తారాల సంఖ్య = \(\frac{(n) !}{p ! q ! r !}\)

(i) మూడు S లను ఒక యూనిట్గా భావిస్తే, మొత్తం అక్షరాలు సంఖ్యలో 10 అవుతుంది. వాటిలో రెండు A లు, రెండు ‘O’ లు, రెండు I లు వున్నాయి.
కనుక ఈ అక్షరాలను అమరిస్తే వచ్చే ప్రస్తారాల సంఖ్య = \(\frac{(10) !}{2 ! 2 ! 2 !}\)
ఇప్పుడు మూడు Sలను వాటిలో వాటిని అమర్చే విధానాలు = \(\frac{3 !}{3 !}\) = 1
∴ కావలసిన ప్రస్తారాల సంఖ్య = \(\frac{(10) !}{(2 !)^3}\)

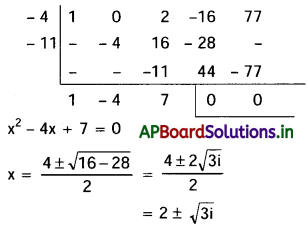
(ii) రెండు ‘A’ లను విడిగా ఉంచితే, మిగిలిన 10 అక్షరాలలో 3’S’ లు, 2’O’ లు 2’T’ లు ఉన్నాయి.
కనుక ఈ 10 అక్షరాలను అమర్చే విధానాలు = \(\frac{(10) !}{3 ! 2 ! 2 !}\)
ఈ పది అక్షరాల మధ్య మధ్యలో, మొదట, చివర కలిపి 11 ఖాళీలున్నాయి.
ఈ 11 ఖాళీలలో రెండు A లను అమర్చే విధానాల సంఖ్య = \(\frac{{ }^{11} P_2}{2 !}\); (రెండు A లే కనుక)
∴ కావలసిన ప్రస్తారాల సంఖ్య = \(\frac{(10) !}{3 ! 2 ! 2 !} \times \frac{{ }^{11} P_2}{2 !}\)

ప్రశ్న 2.
MISSING పదంలోని అక్షరాలలో రెండు S లు ఒకేచోట, రెండు I లు ఒకే చోట కలిసి ఉండేలా ఎన్ని రకాలుగా అమర్చవచ్చు?
సాధన:
MISSING అనే పదంలో 7 అక్షరాలున్నవి. అందు 2I లు 2S లు మిగిలినవి (M, N, G) లు విభిన్నాలు.
రెండు S లు ఒక యూనిట్, రెండు I లు వేరొక యూనిట్ అనుకుంటే, 3 విభిన్న అక్షరాలు, ఈ 5 యూనిట్లు మొత్తం 5.
ఈ ఐదింటిని ఒక వరసలో అమర్చగల విధాల సంఖ్య = 5! = 120
2S లను వాటిలో వాటిని అమర్చే విధాల సంఖ్య = \(\frac{2 !}{2 !}\) = 1
2I లను వాటిలో వాటిని అమర్చే విధాల సంఖ్య = \(\frac{2 !}{2 !}\) = 1
∴ కావలసిన అమరికల సంఖ్య = 5! × 1 × 1 = 120

ప్రశ్న 3.
AJANTA అనే పదంలోని అక్షరాలను ప్రసారించడం ద్వారా వచ్చే పదాలన్నిటినీ నిఘంటువులోని క్రమంలో అమరిస్తే ఆ క్రమంలో కింది పదాల కోటిని కనుక్కోండి.
(i) AJANTA
(ii) JANATA
సాధన:
(i) దత్తపదంలోని అక్షరాల నిఘంటువు క్రమం AAAJNT నిఘంటువులో ముందుగా A లతో మొదలయ్యే పదాలన్నీ వస్తాయి.
కనుక మొదటి స్థానాన్ని Aలో నింపితే దత్త పదం రావటానికి అవకాశమున్నది.
కనుక రెండవ స్థానాన్ని కూడా A తో నింపితే మిగిలిన 4 అక్షరాలను 4! విధాలుగా అమర్చవచ్చు.
ఇదే విధంగా చేసుకొంటూ AJANTA పదం వచ్చే వరకూ కింది విధంగా గణిస్తాం.
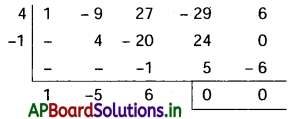
A A – – – – – = 4! = 24
A J A A – – – – = 2! = 2
A J A N A – – = 1 = 1
A J A N T A = 1 = 1
∴ కనుక AJANTA పదం కోటి = 24 + 2 + + 1 = 28

(ii) నిఘంటువులో ముందుగా A లో మొదలయ్యే పదాలన్నీ వస్తాయి.
కనుక మొదటిస్థానాన్ని Aతో నింపితే మిగిలిన అక్షరాలను = \(\frac{5 !}{2 !}\) (ఈ 5 అక్షరాలలో 2A లు ఉన్నాయి.)
ఇదే విధంగా చేసుకొంటూ JANATA పదం వచ్చే వరకూ కింది విధంగా గణిస్తాం.
A – – – – – – = \(\frac{5 !}{2 !}\) = 60
J A A – – – – = 3! = 6
J A N A A – – = 1
JANATA పదం కోటి = 1
∴ JANATA పదం కోటి = 60 + 6 + 1 + 1 = 68

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(c) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(c)

అభ్యాసం – 5(సి)

I.

ప్రశ్న 1.
ఏడుగురు వ్యక్తులను ఒక వృత్తాకార బల్ల చుట్టూ అమర్చే విధానాల సంఖ్య కనుక్కోండి.
సాధన:
వ్యక్తుల సంఖ్య (n) = 7
7 గురు వ్యక్తులు ఒక వృత్తాకార బల్ల చుట్టూ కూర్చునే విధాల సంఖ్య = (n – 1)! = 6! = 720

ప్రశ్న 2.
ఒక రాష్ట్రంలో 10 మంది మంత్రులను, ముఖ్యమంత్రిని ఒక గుండ్రని బల్ల చుట్టూ ముఖ్యమంత్రి ఎప్పుడూ నిర్ధేశించిన స్థానంలో మాత్రమే ఉండేలా ఎన్ని రకాలుగా అమర్చవచ్చు?
సాధన:
మొత్తం వ్యక్తుల సంఖ్య = 1 + 10 = 11
11 మంది వ్యక్తులు ఒక గుండ్రని బల్ల చుట్టూ కూర్చునే విధాల సంఖ్య = (11 – 1)! = 10!
ఈ 11 మంది వ్యక్తులలో ముఖ్యమంత్రి నిర్దేశించిన స్థానంలో మాత్రమే కూర్చోవాలి. కనుక ముఖ్యమంత్రి ఒకే ఒక విధంగా కూర్చోవచ్చు.
∴ కావలసిన వృత్తాకార ప్రసారాల సంఖ్య = (10)! × 1 = (10)!

ప్రశ్న 3.
6 వేర్వేరు రంగుల పూసలలో ఎన్నిరకాలుగా గొలుసులు తయారు చేయవచ్చు? [Mar. ’08]
సాధన:
n విభిన్న వస్తువులతో ఏర్పరచగల వేలాడే రకం వృత్తాకార ప్రస్తారాల సంఖ్య = \(\frac{1}{2}\)(n – 1)!
కనక ఇచ్చిన 6 వేర్వేరు రంగుల పూసలతో ఏర్పరచగల గొలుసుల సంఖ్య = \(\frac{1}{2}\)(6-1)!
= \(\frac{1}{2}\) × 120
= 60

II.

ప్రశ్న 1.
నలుగురు బాలురు, ముగ్గురు బాలికలను ఒక వృత్తం చుట్టూ బాలికలంతా ఒకేచోట ఉండేలా ఎన్నిరకాలుగా అమర్చవచ్చు?
సాధన:
ముగ్గురు బాలికలను ఒక యూనిట్గా నలుగురు బాలురు నాలుగు యూనిట్లు అనుకొంటే ఈ 5 యూనిట్లను ఒక వృత్తాకార బల్ల చుట్టూ అమర్చే విధానాలు సంఖ్య = (5 – 1)! = (4)!
ఇప్పుడు ముగ్గురు బాలికలను వారిలో వారిని (3)! విధాలుగా అమర్చవచ్చు.
ఒక వృత్తం చుట్టూ బాలికలంతా ఒకచోటే ఉండేలా అమర్చగల విధానాల సంఖ్య = 4! × 3!
= 24 × 6
= 144

ప్రశ్న 2.
ఏడుగురు పురుషులు, నలుగురు స్త్రీలను ఒక గుండ్రని బల్ల చుట్టూ ఏ ఇద్దరు స్త్రీలు పక్క పక్కన లేకుండా ఎన్ని రకాలుగా అమర్చవచ్చు? [May ’07]
సాధన:
ముందుగా ఏడుగురు పురుషులు ఒక గుండ్రని బల్ల చుట్టూ అమర్చే విధానాల సంఖ్య (7 – 1)! = 6!
వీరిలో ప్రతి ఇద్దరు పురుషుల మధ్య ఒక్కో ఖాళీ వంతున మొత్తం 7 ఖాళీలు ఉంటాయి. ఈ ఖాళీలను ‘x’ తో గుర్తించటం జరిగింది.

ఇప్పుడు ఈ 7 ఖాళీలలో నలుగురు స్త్రీలను అమర్చే విధానాలు = ⁷P₄
∴ ఏ ఇద్దరు స్త్రీలు పక్క పక్కన లేకుండ అమర్చగల విధానాల సంఖ్య = 6! × ⁷P₄

ప్రశ్న 3.
ఒక గృహస్థుడు, ఏడుగురు’ అతిథులను ఒక గుండ్రటి బల్ల చుట్టూ నిర్దేశించిన ఇద్దరు అతిథులు గృహస్థుడికి ఇరు ప్రక్కలా ఉండేలా ఎన్ని రకాలుగా అమర్చవచ్చు?
సాధన:
మొత్తం వ్యక్తులు = 1 + 7 = 8
ఒక గృహస్థుడు, నిర్దేశించిన ఇద్దరు అతిథులను ఒక యూనిట్ అనుకుందాం. మిగిలిన 5 గురు అతిథులు, ఈ యూనిట్ మొత్తం 6 అవుతాయి.
ఈ ఆరింటిని ఒక గుండ్రటి బల్ల చుట్టూ అమర్చే విధానాల సంఖ్య = (6 – 1)! = 5!
ఇప్పుడు నిర్దేశించిన ఇరువురు వ్యక్తులు వారిలో వారు గృహస్థునికి ఇరువైపుల 2! విధాలుగా కూర్చోవచ్చును.
కావలసిన అమరికల సంఖ్య = 5! × 2!
= 120 × 2
= 240

ప్రశ్న 4.
విభిన్నంగా ఉన్న 3 పసుపు, 4 తెలుపు, 2 ఎరుపు గులాబీలలో ఎర్ర గులాబీలు కలిసి ఉండేలా ఎన్ని దండలు తయారు చేయవచ్చు?
సాధన:
రెండు ఎర్రని గులాబీలను ఒక యూనిట్ అనుకుందాం. అపుడు 3 పసుపు రంగు, 4 తెలుపు రంగు గులాబీలు.
ఒక యూనిట్లో వున్న రెండు ఎర్ర గులాబీలు మొత్తం 8 అవుతాయి. ఈ ఎనిమిదింటితో ఏర్పడే వృత్తాకార ప్రస్తారాల సంఖ్య = \(\frac{1}{2}\)(8 – 1)! = \(\frac{1}{2}\) (7!)
ఇప్పుడు ఒక యూనిట్ లో వున్న రెండు ఎర్ర గులాబీలను వాటిలో వాటిని 2! విధాలుగా అమర్చవచ్చు.
కనుక వృత్తాకార ప్రస్తారాల సంఖ్య = \(\frac{1}{2}\) (7!) × 2!
కాని పువ్వుల దండలు వేలాడే వృత్తాకార ప్రస్తారాల కోవలోకి వస్తాయి. కనుక కావలసిన ప్రస్తారాల సంఖ్య = \(\frac{1}{2}\)(7! × 2!)
= 7!
= 5040

III.

ప్రశ్న 1.
ఆరుగురు బాలురు, ఆరుగురు బాలికలను ఒక గుండ్రని బల్లచుట్టూ
(i) బాలికలంతా ఒకే చోట కలిసి ఉండేలా
(ii) ఏ ఇద్దరు బాలికలు పక్కపక్కన లేకుండా
(iii) బాలురు, బాలికలు ఒకరి తరువాత ఒకరు (ఏకాంతరంగా) వచ్చేలా ఎన్నివిధాలుగా అమర్చవచ్చు?
సాధన:
(i) ఆరుగురు బాలికలను ఒక యూనిట్గా భావిస్తే, అప్పుడు మొత్తం వ్యక్తుల సంఖ్య 6గురు బాలురు + 1 యూనిట్ బాలికలు = 7
వీరిని ఒక వృత్తాకార బల్ల చుట్టూ అమర్చే విధానాలు = (7 – 1)! = 6!
ఇప్పుడు ఆరుగురు బాలికలను వారిలో వారిని 6! విధాలుగా అమర్చవచ్చు.
∴ 6 గురు బాలికలు కలిసి ఒకేచోట ఉండేలా అమర్చగల విధానాల సంఖ్య = 6! × 6!
= 720 × 720
= 5,18,400
(ii) ముందుగా ఆరుగురు బాలురను ఒక వృత్తాకార బల్ల చుట్టూ అమర్చే విధానాలు = (6 – 1)! = 5!
వీరిలో ప్రతి ఇద్దరి బాలుర మధ్య ఒక్కో ఖాళీ వంతున మొత్తం 6 ఖాళీలుంటాయి. ఈ 6 ఖాళీలలో 6 గురు బాలికలను అమర్చే విధానాలు = 6!
∴ ఏ ఇద్దరు బాలికలు ప్రక్క ప్రక్కన లేకుండా అమర్చగల విధానాల సంఖ్య = 5! × 6!
(iii) ఇక్కడ బాలురు, బాలికల సంఖ్య సమానం
బాలురు, బాలికలు ఒకరి తరువాత ఒకరు కూర్చోవాలి అంటే ఏ ఇద్దరు బాలురు ప్రక్కప్రక్కన ఉండకూడదు.
ఏ ఇద్దరు బాలికలు ప్రక్క ప్రక్కన ఉండకూడదు.
ముందుగా ఆరుగురు బాలికలు ఒక గుండ్రని బల్ల చుట్టూ కూర్చున విధాల సంఖ్య = (6 – 1)! = 5!
వీరిలో ప్రతి ఇద్దరి బాలికల మధ్య ఒక్కో ఖాళీ వంతున మొత్తం 6 ఖాళీలు ఉంటాయి: ఈ 6 ఖాళీలను 6 గురు బాలురతో అమర్చే విధాల సంఖ్య 6!
∴ బాలురు, బాలికలు ఒకరి తరువాత ఒకరు వచ్చేలా అమర్చే విధాల సంఖ్య = 5! × 6!

ప్రశ్న 2.
6 విభిన్నమైన ఎర్రగులాబీలు, 3 విభిన్నమైన పసుపు పచ్చ గులాబీలను ఉపయోగించి ఎన్ని దండలు తయారు చేయవచ్చు? వీటిలో ఎన్నింటిలో
(i) పసుపు గులాబీలన్నీ ఒకేచోట ఉంటాయి ?
(ii) ఏ రెండు పసుపు గులాబీలు పక్కపక్కన లేకుండా ఉంటాయి?
సాధన:
6 విభిన్న ఎర్ర గులాబీలు, 3 విభిన్నమైన పసుపు పచ్చ గులాబీలను ఉపయోగించితే ఏర్పడే దండల సంఖ్య = \(\frac{1}{2}\) (6 + 3 – 1)! = \(\frac{1}{2}\)(8!)
(i) 3 విభిన్నమైన పసుపుపచ్చ గులాబీలను ఒక యూనిట్ అనుకుందాం.
6 విభిన్న ఎర్రగులాబీలు, ఒక పసుపు పచ్చ గులాబీల యూనిట్ మొత్తం 7 అవుతాయి.
ఈ ఏడింటితో ఏర్పడే వృత్తాకార ప్రస్తారాల సంఖ్య = \(\frac{1}{2}\) (7 – 1)! = \(\frac{1}{2}\) (6!)
ఇప్పుడు ఒక యూనిట్ వున్న 3 పసుపు పచ్చ గులాబీలు వాటిలో వాటిని 3! విధాలుగా అమర్చవచ్చును.
కనుక మొత్తం వృత్తాకార ప్రస్తారాల సంఖ్య = \(\frac{6 ! \times 3 !}{2}\) = 2,160

(ii) ముందుగా 6 విభిన్న ఎర్రగులాబీలను ఒక దండలో \(\frac{1}{2}\) (6 – 1)! = \(\frac{1}{2}\) (5)! విధాలుగా అమర్చవచ్చు
ఆ తరువాత వాటిమధ్యలో 6 ఖాళీలు ఏర్పడతాయి. ఈ 6 స్థానాలలో 3 విభిన్న గులాబీలను ⁶P₃ విధాలుగా అమర్చవచ్చు.
కనుక వేర్వేరు పసుపు గులాబీలు పక్క పక్కన లేకుండా ఏర్పడే దండాల సంఖ్య = \({ }^6 P_3 \frac{1}{2}(5) !\)
= \(\frac{1}{2}\) × 120 × 120
= 7,200

ప్రశ్న 3.
ముగ్గురు భారతీయులు, ముగ్గురు చైనీయులు, ముగ్గురు కెనడా దేశస్థులు, ఇద్దరు అమెరికా దేశస్థులు ఒకే రౌండ్ టేబుల్ సమావేశానికి వచ్చారు. ఒక దేశానికి చెందిన వారంతా ఒకేచోట కలిసి ఉండేలా వారిని ఒక గుండ్రని బల్ల చుట్టూ ఎన్ని రకాలుగా అమర్చవచ్చు?
సాధన:
ముగ్గురు భారతీయులను ఒక యూనిట్, ముగ్గురు చైనీయులను రెండో యూనిట్గానూ, ముగ్గురు కెనడా దేశస్థులను మూడో యూనిట్గానూ, ఇద్దరు అమెరికా దేశస్థులు నాల్గవ యూనిట్ అనుకుంటే 4 యూనిట్లు అవుతాయి. ఈ నాలుగు యూనిట్లను అమర్చగల విధానాలు (4 – 1)! = 3
ఇప్పుడు ముగ్గురు భారతీయులను వారిలో వారిని అమర్చే విధాల సంఖ్య = 3!
ముగ్గురు చైనీయులను వారిలో వారిని అమర్చే విధాల సంఖ్య = 3!
ముగ్గురు కెనడా దేశస్థులను వారిలో వారిని అమర్చే విధాల సంఖ్య = 3!
ఇద్దరు అమెరికా దేశస్థులను వారిలో వారిని అమర్చే విధాల సంఖ్య = 2!
∴ కావలసిన అమరికల సంఖ్య = 3! × 3! × 3! × 3! × 2!
= 6 × 6 × 6 × 6 × 2
= 2592

ప్రశ్న 4.
6 విభిన్నమైన ఎర్రరంగు పూసలు, మూడు విభిన్నమైన నీలిరంగు పూసలతో ఏ రెండు నీలి రంగు పూసలు పక్క పక్కన లేకుండా ఎన్ని రకాలుగా పూసల గొలుసులు తయారు చేయవచ్చు?
సాధన:
ముందుగా 6 విభిన్నమైన ఎర్రటి పూసలతో ఏర్పడే వృత్తాకార ప్రస్తారాల సంఖ్య = (6 – 1)! = 5! = 120.
ప్రతి రెండు విభిన్న ఎర్రటి పూసల మధ్య ఒక్క ఖాళీచొప్పున మొత్తం 6 ఖాళీలు ఉంటాయి.
ఈ 6 ఖాళీలలో 3 విభిన్న నీలిరంగు పూసలను ⁶P₃ విధాలుగా అమర్చవచ్చు.
కనుక మొత్తం వృత్తాకార ప్రస్తారాల సంఖ్య = 5! × ⁶P₃
కాని పూసల దండలు వేలాడే వృత్తాకార ప్రస్తారాల కోవలోకి వస్తాయి.
కనుక కావలసిన వృత్తాకార ప్రస్తారాల సంఖ్య = \(\frac{1}{2}\) × 5! × ⁶P₃
= \(\frac{1}{2}\) × 120 × 6 × 5 × 4
= 7,200

ప్రశ్న 5.
ఒక కుటుంబంలో ఒక తండ్రి, ఒక తల్లి, ఇద్దరు కుమార్తెలు, ఇద్దరు కుమారులు ఉన్నారు. వీరిలో ఇద్దరు కుమార్తెలు తండ్రికి ఇరుప్రక్కలా ఉండేటట్లుగా ఒక గుండ్రని బల్ల చుట్టూ ఎన్ని రకాలుగా అమర్చవచ్చు?
సాధన:
కుటుంబంలోని సభ్యుల సంఖ్య = 1 + 1 + 2 + 2 = 6
ఇరువురు కుమార్తెలను, తండ్రిని ఒక యూనిట్ అనుకుందాం. తల్లి, ఇరువురు కుమారులు, ఈ యూనిట్ మొత్తం 4.
ఈ నాల్గింటిని ఒక గుండ్రని బల్ల చుట్టూ అమర్చే విధాల సంఖ్య = (4 – 1)! = 3!
ఆ తరువాత ఇరువురు కుమార్తెలు తండ్రికి ఇరువైపుల వారిలో వారు 2! విధాలుగా కూర్చోవచ్చును.
కనుక కావలసిన వృత్తాకార ప్రస్తారాల సంఖ్య = 3! × 2!
= 6 × 2
= 12

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(b)

అభ్యాసం – 5(బి)

I.

ప్రశ్న 1.
పునరావృతాన్ని అనుమతించినపుడు 1, 2, 4, 5, 7, 8 అంకెలనుపయోగించి ఎన్ని 4 అంకెల సంఖ్యలు ఏర్పరచవచ్చు?
సాధన:

పునరావృతాన్ని అనుమతించినపుడు 1, 2, 4, 5, 7, 8 అంకెలను ఉపయోగించి ఏర్పడే 4 అంకెల సంఖ్యల సంఖ్య = 6 × 6 × 6 × 6
= 6⁴
= 1,296

ప్రశ్న 2.
ప్రతి అక్షరాన్ని ఎన్నిసార్లైనా వాడుకొనే పద్ధతిలో RHYME పదంలోని అక్షరాలతో 5 అక్షరాల పదాలు ఎన్ని ఏర్పరచవచ్చు?
సాధన:
RHYME పదంలో 5 అక్షరాలున్నవి.

5 అక్షరాలలో పునరావృతాన్ని అనుమతించినపుడు ఏర్పడే 5 అక్షరాల పదాల సంఖ్య = 5 × 5 × 5 × 5 × 5
= 5⁵
= 3,125

ప్రశ్న 3.
5 మూలకాలున్న సమితి A నుంచి 4 మూలకాలున్న సమితి B కి నిర్వచించగల ప్రమేయాలెన్ని?
సాధన:
A లో వున్న మూలకాల సంఖ్య n(A) = 5
B లో వున్న మూలకాల సంఖ్య n (B) = 4
A నుండి B కు గల ప్రమేయాల సంఖ్య = (n(B))^n(A)
= 4⁵
= 1024

II.

ప్రశ్న 1.
(i) 0, 2, 4, 6, 8 (iii) 1, 3, 5, 7, 9 అంకెలతో ఏర్పడే 6 అంకెల అనులోమ విలోమాల సంఖ్య ఎంత?
సాధన:
అనులోమ విలోమాల సంఖ్య అనగా మొదటి అంకె, ఆరవ అంకె మరియు రెండవ అంకె, అయిదవ అంకె మరియు మూడవ అంకె, నాలుగవ అంకి ఒకే అంకెలు కలిగి ఉండాలి.

(i) ఇచ్చిన అంకెలు 0, 2, 4, 6, 8
6 అంకెల అనులోమ విలోమాల సంఖ్య కొరకు మొదట స్థానాన్ని నింపగల విధానాల సంఖ్య 4 (సున్న కాకుండా) రెండవ స్థానాన్ని నింపగల విధానాల సంఖ్య 5 మరియు మూడవ స్థానాన్ని నింపగల విధానాల సంఖ్య 5.
0, 2, 4, 6, 8 అంకెలతో ఏర్పడే 6 అంకెల అనులోమా, విలోమాల సంఖ్య = 4 × 5² = 100
(ii) ఇచ్చిన అంకెలు 1, 3, 5, 7, 9
6 అంకెల అనులోమ విలోమాల సంఖ్య కొరకు మొదటి స్థానాన్ని నింపగల విధానాల సంఖ్య 5.
రెండువ మరియు మూడవ స్థానాలను కూడా నింపగల విధానాల సంఖ్య 5.
∴ 1, 3, 5, 7, 9 అంకెలతో ఏర్పడే 6 అంకెల అనులోమ విలోమాల సంఖ్యలు 5³ = 125

ప్రశ్న 2.
1, 2, 3, 4, 5, 6 అంకెలనుపయోగించి, కనీసం ఒక అంకె అయినా పునరావృతం అయ్యేలా ఎన్ని 4 అంకెల టెలిఫోన్ నెంబర్లు ఏర్పరచవచ్చు?
సాధన:
6 అంకెలనుపయోగించి పునరావృతాన్ని అనుమతించినపుడు ఏర్పడే 4 అంకెల సంఖ్యలు = 6⁴
పునరావృతం లేనపుడు ఏర్పడే 4 అంకెల సంఖ్యలు ⁶P₄
కనీసం ఒక అంకె అయినా పునరావృతం అయ్యేలా ఏర్పడే 4 అంకెలున్న టెలిఫోన్ నెంబర్లు = 6⁴ – ⁶P₄
= 1296 – 360
= 936

ప్రశ్న 3.
7 మూలకాలున్న సమితి A నుంచి అదే సమితికి ఎన్ని ద్విగుణ ప్రమేయాలు నిర్వచించవచ్చు.
సాధన:
A లోని మూలకాల సంఖ్య n(A) = 7
A నుంచి A కి ద్విగుణ ప్రమేయాల సంఖ్య = n(A)!
= 7!
= 5040

ప్రశ్న 4.
ఇచ్చిన ‘n’ అసరూప వస్తువుల నుంచి ‘r’ వస్తువులతో ఏర్పరచగల ప్రస్తారాలలో ఎన్నింటిలో కనీసం ఒక వస్తువు పునరావృతం అవుతుంది?
సాధన:
‘n’ అసరూప వస్తువుల నుంచి ‘r’ వస్తువులతో ఏర్పరచగల ప్రస్తారాల సంఖ్య.
(i) పునరావృతాన్ని అనుమతించినప్పుడు = n^r
(ii) పునరావృతం అనుమతించనప్పుడు = ⁿP_r
∴ కనీసం ఒక వస్తువు పునరావృతం అయ్యే ప్రస్తారాల సంఖ్య = n^r – ⁿP_r

ప్రశ్న 5.
పునరావృతాన్ని అనుమతించినపుడు NATURE పదంలోని అక్షరాలనుపయోగించి ఏర్పరిచే 5 అక్షరాల పదాలలో ఎన్ని పదాలు N తో మొదలవుతాయి?
సాధన:

మొదటి స్థానాన్ని N తో నింపాలి. ఈ పనిని ఒకే ఒకవిధంగా చేయవచ్చును.
ఆ తరువాత మిగిలిన నాలుగు స్థానాలను పునరావృతాన్ని అనుమతిస్తున్నాం.
కనుక 6 × 6 × 6 × 6 విధాలుగా నింపవచ్చును = 6⁴
∴ N తో మొదలయ్యే 5 అక్షరాల పదాల సంఖ్య = 1 × 6⁴ = 1296

ప్రశ్న 6.
పునరావృతాన్ని అనుమతించినప్పుడు 0, 1, 2, 3, 4, 5 అంకెలతో ఏర్పరచగల 5 అంకెల సంఖ్యలలో 5తో భాగింపబడిన ఎన్ని?
సాధన:
ఒక సంఖ్య 5తో భాగించబడాలంటే చివరి (ఒకట్ల) స్థానంలో 0 లేదా 5 ఉండాలి. అంటే ఆ స్థానాన్ని 2 విధాలుగా నింపవచ్చు.
ఇక మొదటిస్థానంలో సున్నా ఉండకూడదు. కనుక ఆ స్థానాన్ని 1, లేదా 2, లేదా 3, లేదా 4, లేదా 5తో నింపాలి. ఈ పనిని 5 విధాలుగా చేయవచ్చు.
ఇక మిగిలిన స్థానాలను 6 × 6 × 6 విధాలుగా నింపవచ్చు.

కనుక పునరావృతాన్ని అనుమతించినప్పుడు 0, 1, 2, 3, 4, 5, అంకెలలో ఏర్పరచగల 5 అంకెలున్న సంఖ్యలలో 5తో భాగింపబడే సంఖ్యలు = 5 × 6 × 6 × 6 × 2 = 2160

ప్రశ్న 7.
పునరావృతాన్ని అనుమతించినప్పుడు 1, 2, 3, 4 అంకెలను ఉపయోగించి 2000 కన్నా తక్కువగా ఉన్న 4 అంకెల సంఖ్య లెన్ని ఎర్పరచవచ్చు?
సాధన:
అన్ని ఒక అంకె ఉన్న సంఖ్యలు, రెండు అంకెలున్న సంఖ్యలు, మూడు అంకెలున్న సంఖ్యలు మరియు ఒకటితో మొదలైన నాలుగు అంకెలున్న సంఖ్యలు 2000 కన్నా తక్కువగా ఉన్న 4 అంకెల సంఖ్యలు ఏర్పడతాయి.
ఇచ్చిన అంకెలు {1, 2, 3, 4}
ఒక అంకె ఉన్న సంఖ్యలు 4
పునరావృతాన్ని అనుమతించినప్పుడు
రెండు అంకెలున్న సంఖ్యలు = 4 × 4 = 16
మూడు అంకెల సంఖ్యలు 4 × 4 × 4 = 64
ఒకటితో మొదలయ్యే, నాలుగు అంకెల అంకెలున్న సంఖ్యలు

= (1) (4) (4) (4)
= 64
∴ పునరావృతాన్ని అనుమతించినప్పుడు దత్త అంకెలను ఉపయోగించి 2000 కన్న తక్కువగా ఉన్న 4 అంకెల సంఖ్యలు = 4 + 16 + 64 + 64 = 148

III.

ప్రశ్న 1.
ఒక అక్షరమాలలోని 9 విభిన్న అక్షరాలనుపయోగించి 4 అక్షరాల పదాలు ఏర్పరిస్తే వాటిలో ఎన్ని పదాలలో
(i) అక్షరాలు పునరావృతం కాకుండా ఉంటాయి?
(ii) కనీసం ఒక అక్షరం పునరావృతం అవుతుంది.
సాధన:
(i) పునరావృతం కాకుండా 9 విభిన్న అక్షరాల నుండి 4 అక్షరాలతో ఏర్పడే పదాల సంఖ్య = ⁹P₄
= 9 × 8 × 7 × 6
= 3,024
(ii) పునరావృతాన్ని అనుమతిస్తే 9 విభిన్న అక్షరాల నుండి 4 అక్షరాలలో ఏర్పడే పదాల సంఖ్య = 9⁴ = 6561
∴ కనీసం ఒక అక్షరం పునరావృతం అయ్యే విధంగా 9 విభిన్న అక్షరాల నుండి 4 అక్షరాలలో ఏర్పడే పదాల సంఖ్య = 9⁴ – ⁹P₄
= 6561 – 3024
= 3537

ప్రశ్న 2.
పునరావృతాన్ని అనుమతించినప్పుడు 0, 2, 5, 7, 8 అంకెలనుపయోగించి (i) 2 (ii) 4 తో భాగించబడే 4 అంకెల సంఖ్యలు ఎన్ని ఏర్పరచవచ్చు?
సాధన:
(i) మొదటి స్థానాన్ని (వేల స్థానాన్ని) 2 లేదా 5 లేదా 7 లేదా 8తో నింపాలి.

దీనిని 4 విధాలుగా నింపవచ్చు. ఆ తరువాత వందల స్థానాన్ని 5 విధాలుగా, పదుల స్థానాన్ని 5 విదాలుగా నింపవచ్చు.
ఆ తరువాత ఒకట్ల స్థానంలో 0 లేదా 2 లేదా 8 మాత్రమే ఉండాలి. కనుక ఆ స్థానాన్ని 3 విధాలుగా నింపవచ్చు.
కనుక పునరావృతాన్ని అనుమతించినపుడు 4 అంకెలున్న సరిసంఖ్యలు సంఖ్య = 4 × 5 × 5 × 3 = 300
(ii) ఒక సంఖ్య 4తో భాగించబడాలంటే చివరి రెండు స్థానాలలో ఉండే రెండు అంకెల సంఖ్య 4తో భాగించబడాలి.
కనుక ఈ రెండు స్థానాలను 00, 08, 20, 28, 52, 72, 80, 88 చే 8 విధాలుగా నింపవచ్చును.
మొదటి స్థానాన్ని 0 కాకుండా 4 విధులుగా నింపవచ్చు. రెండవ స్థానాన్ని 5 విధులుగా నింపవచ్చును.
∴ 4తో భాగించబడిన 4 అంకెల సంఖ్యలు = 8 × 4 × 5 = 160

ప్రశ్న 3.
0, 1, 2, 3, 4, 5 అంకెలనుపయోగించి, వాడిన అంకెను ఎన్నిసార్లైనా వాడుతూ 6తో భాగింపబడే 4 అంకెల సంఖ్యలను ఎన్నింటిని ఏర్పరచవచ్చు?
సాధన:
ఇచ్చిన అంకెలు 0, 1, 2, 3, 4, 5 కావలసిన 4 అంకెల సంఖ్య కొరకు మొదట స్థానాన్ని సున్నాకా కుండ మిగిలిన అంకెలతో నింపగల విధానాల సంఖ్య 5. (పునరావృతాన్ని అనుమతించినపుడు)
రెండవ స్థానాన్ని నింపగల విధానాల సంఖ్య 6. ఇదేవిధంగా మూడవ స్థానాన్ని నింపగల విధానాల సంఖ్య 6.
ఈ విధంగా నింపిన తరువాత చివర స్థానాన్ని ఒక్కొక్క అంకెలతో నింపగా 6 వరుస సంఖ్యలు వచ్చును.
ఈ ఆరు వరుస సంఖ్యలలో ఖచ్చితంగా ఒక సంఖ్య 6 చే భాగించబడును.
∴ 0, 1, 2, 3, 4, 5 అంకెలనుపయోగించి, వాడిన అంకెను ఎన్ని సార్లైనా వాడుతూ 6 తో భాగింపబడే 4 అంకెల సంఖ్యలు = 5 × 6 × 6 × 1 = 1800

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(a)

అభ్యాసం – 5(ఎ)

I.

ప్రశ్న 1.
ⁿP₃ = 1320 అయితే n విలువ కనుక్కోండి.
సాధన:
సూచన : ⁿP_r = \(\frac{n !}{(n-r) !}\) = n(n – 1) (n – 2)…….(n – r + 1)
ⁿP₃ = 1320
= 10 × 132
= 10 × 12 × 11
= 12 × 11 × 10
= ¹²P₃
∴ n = 12

ప్రశ్న 2.
ⁿP₇ = 42 . ⁿP₅, అయితే n ఎంత? (May ’11, ’07)
సాధన:
ⁿP₇ = (42) . ⁿP₅
⇒ (n)(n – 1) (n – 2) (n – 3) (n – 4) (n – 5) (n – 6) = 42 (n) (n – 1) (n – 2) (n – 3) (n – 4)
⇒ (n – 5) (n – 6) = 42
⇒ (n – 5) (n – 6) = 7 × 6
⇒ n – 5 = 7 లేదా n – 6 = 6
⇒ n = 12

ప్రశ్న 3.
⁽ⁿ⁺¹⁾P₅ : ⁿP₆ = 2 : 7 అయితే n విలువ కనుక్కోండి. [Mar. ’07]
సాధన:

⇒ 2(n² – 9n + 20) = 7n + 7
⇒ 2n² – 22n – 3n + 33 = 0
⇒ 2n² – 25n + 33 = 0
⇒ 2n(n – 11) – 3(n – 11) = 0
⇒ (n – 11) (2n – 3) = 0
⇒ n = 11 లేదా n = \(\frac{3}{2}\)
∴ n ధన పూర్ణాంకం కనుక n = 11

ప్రశ్న 4.
¹²P₅ + 5 . ¹²P₄ = ¹³P_r, అయితే r విలువ ఎంత?
సాధన:

ప్రశ్న 5.
¹⁸P_r-1 : ¹⁷P_r-1 = 9 : 7, అయితే r విలువను కనుక్కోండి.
సాధన:

ప్రశ్న 6.
ఒక వ్యక్తికి నలుగురు కొడుకులున్నారు. అతడికి అందుబాటులో 5 పాఠశాలలున్నాయి. ఏ ఇద్దరు పిల్లలు ఒకే పాఠశాలలో లేకుండా ఆ వ్యక్తి తన పిల్లలను ఎన్ని విధాలుగా పాఠశాలలో చేర్చవచ్చు?
సాధన:
ఏ ఇద్దరు పిల్లలు ఒకే పాఠశాలలో లేకుండా ఒక వ్యక్తి తన 4 గురు కొడుకులను 5 పాఠశాలలో చేర్చే విధాల సంఖ్య = ⁵P₄
= 5 × 4 × 3 × 2
= 120

II.

ప్రశ్న 1.
ఒక రైల్వే లైనులో 25 స్టేషన్లున్నాయి. ఈ స్టేషన్లలో ఒక స్టేషన్ నుంచి మరొక స్టేషన్కు వెళ్ళడానికి అనుమతించేలా ఎన్ని విభిన్న రకాల రెండోతరగతి టిక్కెట్లు ముద్రించాలి?
సాధన:
రైల్వే లైనులో గల స్టేషన్ల సంఖ్య = 25
ఒక స్టేషన్ నుండి మరొక స్టేషన్కు వెళ్ళడానికి అనుమతించే రెండో తరగతి టిక్కెట్ల సంఖ్య = ²⁵P₂
= 25 × 24
= 600

ప్రశ్న 2.
ఒక తరగతిలో 30 మంది విద్యార్థులున్నారు. ప్రతి విద్యార్థి తన సహాధ్యాయులకు ఒక్కొక్కరికి నూతన సంవత్సర శుభాకాంక్షలతో ఒక కార్డు చొప్పున పంపించాలంటే మొత్తం ఎన్ని కార్డులు కావాలి?
సాధన:
తరగతిలో విద్యార్థుల సంఖ్య = 30
ప్రతి విద్యార్థి తన సహాధ్యాయులకు ఒక్కొక్కరికి నూతన సంవత్సర శుభాకాంక్షలతో ఒక కార్డు వంతున పంపించాలంటే కావలసిన కార్డుల సంఖ్య = ³⁰P₂
= 30 × 29
= 870

ప్రశ్న 3.
TRIANGLE పదంలోని అక్షరాలను అచ్చుల స్థానాల్లో ఎప్పుడూ అచ్చులు ఉండేలా ఎన్ని విధాలుగా అమర్చవచ్చు?
సాధన:
TRIANGLE అనే పదంలో 3 అచ్చులు (I, A, E), 5 హల్లులు (T, R, N, G, L) ఉన్నాయి.

అచ్చుల స్థానాల్లో ఎప్పుడు అచ్చులే ఉండాలి. కనుక 3 అచ్చులను వాటి వాటి స్థానాల్లో 3! విధాలుగా అమర్చవచ్చు.
ఆ తరువాత మిగిలిన 5 స్థానాల్లో 5 హల్లులను 5! విధాలుగా అమర్చవచ్చు.
కనుక అచ్చుల స్థానాలను మార్చకుండా ఏర్పడే ప్రస్తారాల సంఖ్య = (3!) (5!)
= (6) (120)
= 720

ప్రశ్న 4.
0, 2, 4, 7, 8 అంకెలతో ఏర్పరచగలిగే 4 అంకెల సంఖ్యల మొత్తాన్ని కనుక్కోండి. (పునరావృతం కానట్లుగా)
సాధన:
మొదటి పద్ధతి:
0, 2, 4, 7, 8 అంకెలతో ఏర్పడే 4 అంకెల సంఖ్యల సంఖ్య = ⁵P₄ – ⁴P₃
= 120 – 24
= 96

ఈ 96 సంఖ్యలలో
⁴P₃ – ³P₂ సంఖ్యలలో 2 యూనిట్ల స్థానంలో ఉంటుంది.
⁴P₃ – ³P₂ సంఖ్యలలో 2 పదుల స్థానంలో ఉంటుంది.
⁴P₃ – ³P₂ సంఖ్యలలో 2 వందల స్థానంలో ఉంటుంది.
⁴P₃ సంఖ్యలలో 2 వేల స్థానంలో ఉంటుంది.
∴ 2 వల్ల వచ్చే మొత్తం = (⁴P₃ – ³P₂) 2 + (⁴P₃ – ³P₂) 20 +(⁴P₃ – ³P₂) 200 + ⁴P₃ × 2000
= ⁴P₃ (2 + 20 + 200 + 2000) – ³P₂ (2 + 20 + 200)
= 24(2222) – 6(222)
= 24 × 2 × 1111 – 6 × 2 × 111
ఇదే విధంగా 4 వల్ల వచ్చే మొత్తం = 24 × 4 × 1111 – 6 × 4 × 111
7 వల్ల వచ్చే మొత్తం = 24 × 7 × 1111 – 6 × 7 × 111
8 వల్ల వచ్చే మొత్తం = 24 × 8 × 1111 – 6 × 8 × 111
∴ 96 సంఖ్యల మొత్తం = (24 × 1111) (2 + 4 + 7 + 8) – (6 × 111) (2 + 4 + 7 + 8)
= 26,664 (21) – 666 (21)
= 21 (26664 – 666)
= 21 (25,998)
= 5,45,958

రెండో పద్ధతి:
ఇచ్చిన n అంకెలలో ‘0’ కూడా ఉంటే, ఈ ‘n’ అంకెలతో ఏర్పరచగల ‘r’ అంకెల సంఖ్యల మొత్తం = ^(n-1)P_(r-1) × దత్త అంకెల మొత్తం × {111…. 1 (r – 1 సార్లు)} (r – 1)
= ^(n-1)P_(r-2) × దత్త అంకెల మొత్తం × {111……..1 (r సార్లు)} (r – 2)
ఇచ్చట n = 5, r = 4, ఇచ్చిన అంకెలు {0, 2, 4, 7, 8}
కనుక {0, 2, 4, 7, 8} అంకెలతో ఏర్పరచగలిగే, 4 అంకెల సంఖ్యల మొత్తం = ^(5-1)P_(4-1) × (0 + 2 + 4 + 7 + 8) × (1111) (4 – 1)
= ^(5-2)P_(r-2) × (0 + 2 + 4 + 7 + 8) × (111) (4 – 2)
= ⁴P₃ (21) (1111) – ³P₂ (21) (111)
= 21 [24 × 1111 – 6 × 111]
= 21 [26664 – 666]
= 21 (25 998)
= 5,45,958

ప్రశ్న 5.
0, 2, 4, 6, 8 అంకెలతో (వాడిన అంకెను వాడకుండా) 4000 కన్నా పెద్ద సంఖ్యలు ఎన్ని ఏర్పరచవచ్చు?
సాధన:
దత్త అంకెలలో ఏర్పడే 5 అంకెల సంఖ్యలు ప్రతీది 4000 కంటే పెద్దది అవుతుంది.
అయితే మొదటి స్థానాన్ని తప్ప మిగిలిన అంకెలలో {2, 4, 6, 8} నింపాలి.
కనుక పదివేల స్థానాన్ని (మొదటి స్థానాన్ని) 4 విధాలుగా నింపవచ్చు.
కనుక 5 అంకెలున్న సంఖ్యలు 4 × 4! = 4 × 24 = 96.
4, 6, 8 తో మొదలయ్యే ప్రతి నాలుగు అంకెల సంఖ్య 4000 కంటే పెద్దది అవుతుంది.
కనుక వేల స్థానాన్ని 3 విధాలుగా నింపవచ్చు. మిగిలిన 3 స్థానాలను మిగిలిన 4 అంకెలతో AP విధాలుగా నింపవచ్చు.
కనుక 4000 కన్నా పెద్దవైన 4 అంకెలున్న స్థానాలు 3 × ⁴P₃ = 3 × 24 = 72
∴ 4000 కన్నా పెద్దవైన సంఖ్యలు = 96 + 72 = 168

ప్రశ్న 6.
MONDAY పదంలోని అక్షరాలను అచ్చులు ఎప్పుడూ బేసిస్థానాల్లో ఉండేలా ఎన్ని రకాలుగా అమర్చవచ్చు?
సాధన:
MONDAY పదంలో 2 అచ్చులు (O, A) 4 హల్లులు (M, N, D, Y) ఉన్నాయి.
MONDAY పదంలో 6 అక్షరాలున్నవి. అందు 3 సరిస్థానాలు, 3 బేసి స్థానాలు 3 సరిస్థానాల్లో 2 అచ్చులను ³P₂ విధాలుగా అమర్చవచ్చు.
మిగిలిన 4 స్థానాలలో 4 హల్లులను 4! విధాలుగా అమర్చవచ్చు.
ప్రాథమిక సూత్రం ప్రకారం ఈ రెండు పనులను ³P₂ × 4! విధాలుగా చేయవచ్చు.
కనుక అచ్చులు ఎల్లప్పుడూ సరిస్థానాలలో ఉండేలా అమర్చే విధాల సంఖ్య = ³P₂ × 4!
= 3! x 4!
= 6 × 24
= 144

ప్రశ్న 7.
5 విభిన్న గణిత పుస్తకాలు, 4 విభిన్న భౌతిక శాస్త్ర పుస్తకాలు, 3 విభిన్న రసాయన శాస్త్ర పుస్తకాలను ఒక వరసలో ఒక శాస్త్రానికి సంబంధించిన పుస్తకాలన్నీ ఒకేచోట కలిసి ఉండేలా ఎన్ని రకాలుగా అమర్చవచ్చు?
సాధన:
5 విభిన్న గణిత పుస్తకాలు ఒక యూనిట్, 4 విభిన్న భౌతిక శాస్త్ర పుస్తకాలు ఒక యూనిట్, 3 విభిన్న రసాయన శాస్త్ర పుస్తకాలు ఒక యూనిట్ అనుకుంటే 3 యూనిట్లను ఒక వరుస క్రమములో 3! విధాలుగా అమర్చవచ్చు. ఆ తరువాత ఒక యూనిట్లలోని 5 విభిన్న గణిత పుస్తకాలను వాటిలో వాటిని 5! విధాలుగా, వేరొక యూనిట్ లోని 4 విభిన్న భౌతిక శాస్త్ర పుస్తకాలను వాటిలో వాటిని 4! విధాలుగా, మరొక యూనిట్లో ఉన్న 3 విభిన్న రసాయనశాస్త్ర పుస్తకాలను 3! విధాలుగా అమర్చవచ్చు.
∴ ఒక వరుసలో ఒక శాస్త్రానికి సంబంధించిన పుస్తకాలన్నీ ఒకేచోట కలిసి ఉండేలా అమర్చే విధాల సంఖ్య = 3! × 5! × 4! × 3!

III.

ప్రశ్న 1.
CONSIDER పదంలోని అక్షరాలనుపయోగించి ఎన్ని 5 అక్షరాల పదాలు ఏర్పరచవచ్చు? వాటిలో ఎన్ని పదాలు ‘C’ తో మొదలవుతాయి? ఎన్ని పదాలకు R అక్షరం చివరి అక్షరం అవుతుంది? ఎన్ని పదాలు ‘C’ తో మొదలయి తో అంతమవుతాయి?
సాధన:
CONSIDER అనే పదంలో 8 విభిన్న అక్షరాలున్నాయి.
(i) 5 అక్షరాలతో ఏర్పడే పదాల సంఖ్య
⁸P₅ = 8 × 7 × 6 × 5 × 4 = 6,720

(ii)
‘C’ తో మొదలయ్యే 5 అక్షరాలున్న పదాల సంఖ్య = 1 × ⁷P₄
= 7 × 6 × 5 × 4
= 840

(iii)
‘R’ తో అంతమయ్యే 5 అక్షరాలున్న పదాల సంఖ్య = 1 × ⁷P₄ = 840

(iv)
‘C’ తో మొదలయి ‘R’ తో అంతమయ్యే 5 అక్షరాలున్న పదాల సంఖ్య = ⁶P₃
= 6 × 5 × 4
= 120

ప్రశ్న 2.
A₁, A₂, A₃,……., A₁₀ అనే 10 మంది విద్యార్థులను ఒక వరుసలో
(i) A₁, A₂, A₃ లు కలిసి ఉండేటట్లు
(ii) A₁, A₂, A₃ లు నిర్దేశించిన క్రమంలో ఉండేటట్లు
(iii) A₁, A₂, A₃, లు ‘నిర్దేశించిన క్రమంలో కలిసి ఉండేటట్లు ఎన్నివిధాలుగా అమర్చవచ్చు?
సాధన:
(i) A₁, A₂,……., A₁₀ లు 10 మంది విద్యార్ధులు.
A₁, A₂, A₃ లను ఒక యూనిట్గా అనుకుంటే, మిగిలిన 7 గురు, ఈ ఒక యూనిట్ మొత్తం 8 అవుతాయి.
ఈ ఎనిమిదింటిని 8! విధాలుగా అమర్చవచ్చు. ఇపుడు ఒక యూనిట్లో వున్న A₁, A₂, A₃ లను వారిలో వారిని 3! విధాలుగా అమర్చవచ్చు.
కనుక ప్రాథమిక సూత్రం ప్రకారం, ఈ రెండు పనులను (8!) (3!) విధాలుగా అమర్చవచ్చును.

(ii) A₁, A₂, A₃ లు నిర్దేశించిన క్రమంలో ఉండేటట్లు అమర్చినివి.
A₁, A₂, A₃ లను 10 స్థానాలలో నిర్దేశించిన ప్రకారం అమర్చే విధాల సంఖ్య = \(\frac{{ }^{10} P_3}{3 !}\)
మిగిలిన 7 గురుని మిగిలిన స్థానాలలో అమర్చే విధాల సంఖ్య = 7!
∴ A₁, A₂, A₃ లు ఒక నిర్దేశించిన ప్రకారం అమర్చే విధాల సంఖ్య

(iii) A₁, A₂, A₃ లు నిర్దేశించిన క్రమంలో కలిసి ఉండేటట్లు అమర్చాలి.
A₁, A₂, A₃ లను ఒక యూనిట్ అనుకుంటే, మిగిలిన 7 గురు, ఈ ఒక యూనిట్ మొత్తం 8 అవుతాయి.
ఈ ఎనిమిదింటిని ఒక వరస క్రమంలో (8)! విధాలుగా అమర్చవచ్చును.
A₁, A₂, A₃ లు నిర్దేశించిన క్రమంలో కలిసి ఉండాలి కనుక వారిలో వారు తమ తమ స్థానాలను మార్చుకోవటానికి వీలులేదు.
కనుక కోరిన ప్రకారం అమర్చే విధాల సంఖ్య = 8!

ప్రశ్న 3.
5 విభిన్న ఎర్రబంతులు, 4 విభిన్న నల్ల బంతులను ఒక వరుసలో
(i) ఏ రెండు ఒకే రంగు బంతులు పక్క పక్కన లేకుండా
(ii) ఒకే రంగు బంతులన్నీ ఒక చోట ఉండేటట్లు ఎన్ని విధాలుగా అమర్చవచ్చు.
సాధన:
ఎర్రబంతుల సంఖ్య = 5
నల్లబంతుల సంఖ్య = 4
(i) ఏ రెండు ఒకే రంగు బంతులు పక్క ప్రక్కన లేకుండా కావలసిన అమరిక కొరకు ముందుగా నలుగు నల్లని బంతులను అమ్మగల విధానాల సంఖ్య 4!

వాటి మధ్యగల 5 ఖాళీ స్థానాలలో 5 ఎర్రని బంతులను అమర్చగల విధానాల సంఖ్య 5!
∴ ఏ రెండు ఒకేరంగు బంతులు పక్క పక్కన లేకండా అమర్చగల విధానాల సంఖ్య = 4! 5!

(ii) ఒకే రంగు, బంతులన్నీ ఒక చోట ఉండేటట్లు 4 నల్లని బంతులు ఒక యూనిట్ గాను, 5 ఎర్రబంతులను ఒక యూనిట్గాను అనుకుంటే ఈ రెండు యూనిట్లను అమర్చగల విధానాల సంఖ్య 2!.
నాలుగు నల్ల బంతులను వాటి వాటిని మార్చి అమర్చగల విధానాల సంఖ్య 4! అయిదు ఎర్రబంతులను వాటిలో వాటిని మార్చి అమర్చగల విధానాల సంఖ్య = 5!

ప్రశ్న 4.
1, 2, 5, 6, 7 అంకెలనుపయోగించి (i) 2 (ii) 3 (iii) 4 (iv) 5 (v) 25 తో భాగించబడే 4అంకెల సంఖ్యలు ఎన్ని ఏర్పరచవచ్చు?
సాధన:
1, 2, 5, 6, 7 అంకెలనుపయోగించితే ఏర్పడే నాలుగు అంకెలున్న సంఖ్యలు = ⁵P₄ = \(\frac{5 !}{1 !}\) = 120.
(i) ఆ విధంగా ఏర్పడిన 4 అంకెలున్న సంఖ్య 2తో భాగింపబడ వలయునన్న దాని చివరి (ఒకట్ల) స్థానంలో సరి సంఖ్య ఉండాలి.
ఆ స్థానాన్ని 2 లేదా 6తో నింపవచ్చు ఇప్పుడు మిగిలిన 3 స్థానాలను

మిగిలిన 4 అంకెలతో ⁴P₃ విధాలుగా నింపవచ్చు. కనుక 2తో భాగింపబడే 4 అంకెల సంఖ్యల సంఖ్యలు = 2 × ⁴P₃
= 2 × 4!
= 2(24)
= 48

(ii) ఒక సంఖ్య 3తో భాగింపబడడానికి, ఆ సంఖ్యలోని అంకెల మొత్తం 3తో భాగించబడాలి.
మనకు ఇచ్చిన 5 అంకెల మొత్తం 21 కనుక వీటి నుంచి 4 అంకెలను మొత్తం 3తో భాగించబడే విధంగా ఎంచుకోవాలి అంటే 1, 2, 5, 7 లను ఎన్నుకోవాలి వాటి మొత్తం 15 కనుక
∴ 3తో భాగింపబడే నాలుగు అంకెలున్న సంఖ్యలు = 4! = 24

(iii) ఒక సంఖ్య 4తో భాగించబడాలంటే చివరి రెండు స్థానాల్లో (అంటే పదులు, ఒకట్ల స్థానాల్లో) ఉన్న రెండు అంకెల సంఖ్య 4తో భాగించబడాలి.
కనుక ఆ రెండు స్థానాలను 12, 16, 52, 56, 72, 76 అనే సంఖ్యలతో నింపాలి. అంటే 6 విధాలుగా ఆ రెండు స్థానాలు నింపవచ్చు.
ఇప్పుడు మిగిలిన రెండు స్థానాలను మిగిలిన 3అంకెలలో 3P2 విధాలుగా నింపవచ్చు. కనుక 4తో భాగింపబడే 4 అంకెల సంఖ్యల సంఖ్య = 6 × ³P₂
= 6 × 3!
= 6 × 6
= 36

(iv) ఒక సంఖ్య 5తో భాగించబడాలంటే చివరి (ఒకట్ల) స్థానంలో 5 ఉండాలి. (‘0’ కూడా ఉండవచ్చు. కాని ఇచ్చిన అంకెలలో సున్నా లేదు)
కనుక ఒకట్ల స్థానంలో 5 ఉంచితే మిగిలిన 3 స్థానాలను మిగిలిన 4 అంకెలతో ⁴P₂ విధాలుగా నింపవచ్చు.
5తో భాగింపబడే 4 అంకెల సంఖ్యల సంఖ్య = ⁴P₃ = 4! = 24

(v) ఒక సంఖ్య 25తో భాగించబడాలంటే చివరి రెండు స్థానాలలో 25 లేదా 75తో నింపాలి. (50 లేదా 00 తో కూడా నింప వచ్చు. కాని దత్త అంకెలలో ‘0’ లేదు)
అంటే ఈ స్థానాలు 2 విధాలుగా నింపవచ్చు.
ఇపుడు మిగిలిన రెండు స్థానాలను మిగిలిన 3 అంకెలలో ³P₂ విధాలుగా నింపవచ్చు.
∴ 25తో భాగింపబడే 4 అంకెల సంఖ్యల సంఖ్య 2 × ³P₂
= 2 × 3!
= 2 × 6
= 12

ప్రశ్న 5.
MASTER పదంలోని అక్షరాలను ప్రసారించడం వల్ల వచ్చే పదాలను నిఘంటువు క్రమంలోరాస్తే ఆ వరుసలో (i) REMAST (ii) MASTER పదాల కోటిలను కనుక్కోండి. [(May ’11); T.S. Mar. ’16; Mar. ’08, ’07; May ’06’ 11, ’08, ’07]
సాధన:
దత్త పదం MASTER లోని అక్షరాల నిఘంటువు క్రమం
A E M R S T

కనుక REMAST అనే పదం కోటి = 3 × 5! + 1 × 4! + 1 × 3! + 1
= 3(120) + 24 + 6 + 1
= 360 + 24 + 6 + 1
= 391

(ii) నిఘంటువులో ముందుగా A లో, తరువాత E లో, ఆ తరువాత M తో మొదలయ్యే పదాలు వస్తాయి.
వీటిలోనే మనకు కావలసిన పదం MASTER ఉంది.
కనుక వీటి నిఘంటువు క్రమాన్ని గమనిస్తే, వీటిలో ముందుగా MA తో మొదలయ్యేవి వస్తాయి.
ఈ విధంగా MASTER అనే పదం వచ్చేంత వరకు లెక్కించాలి.

కనుక MASTER అనే పదం కోటి = 2 × 5! + 2 × 3! + 2 × 2! + 1
= 2 (120) + 2(6) + 2 × 2 + 1
= 240 + 12 + 4 + 1
= 257

ప్రశ్న 6.
BRING అనే పదంలోని అక్షరాలను వివిధ రకాలుగా అమరిస్తే వచ్చే పదాలను నిఘంటువు క్రమంలో రాసినప్పుడు ఆ క్రమంలో 59వ పదం ఏది?
సాధన:
BRING అనే పదంలో అక్షరాలు నిఘంటువు క్రమం
B, G, I, N, R

∴ 59వ పదం IGRBN అవుతుంది.

ప్రశ్న 7.
1, 2, 4, 5, 6 అంకెలతో ఏర్పరచగలిగే నాలుగు అంకెల సంఖ్యల మొత్తాన్ని కనుక్కోండి. (పునరావృతం కాకుండా)
సాధన:
మొదటి పద్ధతి:
1, 2, 4, 5, 6 అనే 5 అంకెలతో ఏర్పరచగల 4 అంకెల సంఖ్యల సంఖ్య = ⁵P₄ = 5! = 120
ముందుగా ఈ 120 సంఖ్యల మొత్తం కనుక్కోవాలి. ముందుగా ఈ 120 సంఖ్యల ఒకట్ల స్థానంలోని అంకెల మొత్తం కనుక్కొందాం.
ఒకట్ల స్థానంలో 1 ఉంచితే మిగిలిన 3 స్థానాలను మిగిలిన 4 అంకెలతో ⁴P₃ విధాలుగా నింపవచ్చు.
అంటే పైన చెప్పిన 120 నాలుగు అంకెల సంఖ్యలలో ⁴P₃ సంఖ్యల ఒకట్ల స్థానంలో 1 వస్తుంది.
ఇట్లే 2, 4, 5, 6 అంకెలు ఒక్కొక్కటి ⁴P₃ సార్లు ఒకట్ల స్థానంలో వస్తాయి.
ఈ అంకెలన్నీ కలిపితే మనకు 120 సంఖ్యల ఒకట్ల స్థానంలోని మొత్తం = ⁴P₃ × 1 + ⁴P₃ × 2 + ⁴P₃ × 4 + ⁴P₃ × 5 + ⁴P₃ × 6
= ⁴P₃ (1 + 2 + 4 + 5 + 6)
= ⁴P₃ (18)
ఇదే విధంగా ఈ 120 సంఖ్యల పదుల స్థానంలో కూడా పైన చెప్పిన అంకెలు మాత్రమే వస్తాయి.
కనుక పదుల స్థానంలోని అంకెల మొత్తం కూడా ⁴P₃ (18).
కాని పదుల స్థానంలోని మొత్తం కనుక దాని విలువ = ⁴P₃ (1 + 2 + 4 + 5 + 6) 10 = ⁴P₃ (18) (10)
ఇలాగే వందల స్థానంలోని అంకెల మొత్తం విలువ = ⁴P₃ × 18 × 100
వేల స్థానంలోని అంకెల మొత్తం విలువ = ⁴P₃ × 18 × 1000
∴ 1, 2, 4, 5, 6 అంకెలతో ఏర్పడే 4 అంకెల సంఖ్యల మొత్తం = ⁴P₃ × 18 × 1 + ⁴P₃ × 18 × 10 + ⁴P₃ (18) (100) + ⁴P₃ (18) (1000)
= ⁴P₃ × 18 (1 + 10 + 100 + 1000)
= 24 × 18 × 1111
= 4,79,952
రెండో పద్ధతి :
n శూన్యేతర అంకెలను ఉపయోగించి ఏర్పర్చ గల ‘r’ అంకెల సంఖ్యల మొత్తం = ^(n-1)P_(r-1) × దత్త n అంకెల మొత్తం × (111…….1) r సార్లు
ఇచ్చట n = 5, r = 4, దత్త అంకెలు = {1, 2, 4, 5, 6}
∴ {1, 2, 4, 5, 6} అంకెలతో ఏర్పరచగలిగే 4 అంకెల సంఖ్యల మొత్తం (పునరావృతం కాకుండా) = ^(5-1)P_(4-1) × (1 + 2 + 4 + 5 + 6) × (1111)
= ⁴P₃ × 18 × 1111
= 24 × 18 × 1111
= 4,79,952

ప్రశ్న 8.
9 వస్తువులు, 9 పెట్టెలు కలవు. వాటిలో 5 వస్తువులు మూడు చిన్న పెట్టెలలో సరిపోవు. ఒక్కొక్క పెట్టెలో ఒక్కొక్క వస్తువు ఉండేట్లుగా ఎన్ని విధాలుగా అమర్చవచ్చు.
సాధన:
వస్తువుల సంఖ్య = 9
పెల సంఖ్య = 9
కావలసిన అమరిక కొరకు, 9 వస్తువులలో 5 వస్తువులు మూడు చిన్న పెట్టిలలో సరిపోవు.
కనుక అయిదు వస్తువులను 6 పెట్టెలలో అమర్చగల విధానల సంఖ్య = ⁶P₅
మిగిలిన 4 వస్తువులను 4 పెట్టెలలో అమర్చగల విధానాల సంఖ్య = 4!
కావలసిన అమరికల సంఖ్య = ⁶P₅ 4!

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 4 సమీకరణ వాదం Exercise 4(d) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 4 సమీకరణ వాదం Exercise 4(d)

అభ్యాసం – 4(డి)

I.

ప్రశ్న 1.
x³ + 2x² – 4x + 1 = 0 సమీకరణపు మూలాలకు 3 రెట్లున్న మూలాలు గల బీజీయ సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x³ + 2x² – 4x + 1 = 0 అనుకొనుము.
∴ కావలసిన సమీకరణం f(\(\frac{x}{3}\)) = 0
\(\left(\frac{x}{3}\right)^3+2\left(\frac{x}{3}\right)^2-\frac{4 x}{3}+1=0\)
\(\frac{x^3}{27}+\frac{2}{9} x^2-\frac{4}{3} x+1=0\)
27 గుణించగా
కావలసిన సమీకరణం x³ + 6x² – 36x + 27 = 0

ప్రశ్న 2.
x⁵ – 2x⁴ + 3x³ – 2x² + 4x + 3 = 0 సమీకరణపు మూలాలకు 2 రెట్లున్న మూలాలు గల బీజీయ సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x⁵ – 2x⁴ + 3x³ – 2x² + 4x + 3 = 0
f(\(\frac{x}{2}\)) = 0 సమీకరణం కావలసిన లక్షణాలలో ఉంటుంది.
కావలసిన సమీకరణం f(\(\frac{x}{3}\)) = 0
⇒ \(\left(\frac{x}{2}\right)^5-2\left(\frac{x}{2}\right)^4+3\left(\frac{x}{2}\right)^3-2\left(\frac{x}{2}\right)^2+4\left(\frac{x}{2}\right)\) + 3 = 0
⇒ \(\frac{x^5}{32}-2 \cdot \frac{x^4}{16}+3 \cdot \frac{x^3}{8}-2 \cdot \frac{x^2}{4}+4 \cdot \frac{x}{2}+3=0\)
32 చే గుణించగా
కావలసిన సమీకరణం x⁵ – 4x⁴ + 12x³ – 16x² + 64x + 96 = 0

ప్రశ్న 3.
x⁴ + 5x³ + 11x + 3 = 0 సమీకరణ మూలాలకు వ్యతిరేక గుర్తులు కలిగిన సంఖ్యలు మూలాలుగా గల రూపాంతర సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x⁴ + 5x³ + 11x + 3 = 0
-α₁, -α₂, -α₃, -α₄ లు మూలాలుగా గల సమీకరణం f(-x) = 0
⇒ (-x)⁴ + 5(-x)³ + 11(-x) + 3 = 0
⇒ x⁴ – 5x³ – 11x + 3 = 0

ప్రశ్న 4.
x⁷ + 3x⁵ + x³ – x² + 7x + 2 = 0 సమీకరణం మూలాలకు వ్యతిరేక గుర్తులు కలిగిన సంఖ్యలు మూలాలుగా గల రూపాంతర సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x⁷ + 3x⁵ + x³ – x² + 7x + 2 = 0
-α₁, -α₂, …….., -α₇ లు మూలాలుగల
సమీకరణం f(-x) = 0
⇒ (-x)⁷ + 3(-x)⁵ + (-x)³ – (-x)² + 7(-x) + 2 = 0
⇒ -x⁷ – 3x⁵ – x³ – x² – 7x + 2 = 0
⇒ x⁷ + 3x⁵ + x³ + x² + 7x – 2 = 0

ప్రశ్న 5.
x⁴ – 3x³ + 7x² + 5x – 2 = 0 సమీకరణ మూలాల వ్యుత్కమాలు మూలాలుగా గల బహుపది సమీకరణాన్ని కనుక్కోండి. [Mar. ’11]
సాధన:
దత్త సమీకరణం f(x) = x⁴ – 3x³ + 7x² + 5x – 2 = 0
కావలసిన సమీకరణం f(\(\frac{1}{x}\)) = 0
⇒ \(\frac{1}{x^4}-\frac{3}{x^3}+\frac{7}{x^2}+\frac{5}{x}-2=0\)
x⁴ చే గుణించగా
⇒ 1 – 3x + 7x² + 5x³ – 2x⁴ = 0
⇒ 2x⁴ – 5x³ – 7x² + 3x – 1 = 0

ప్రశ్న 6.
x⁵ + 11x⁴ + x³ + 4x² – 13x + 6 = 0 సమీకరణం మూలాల వ్యుత్కమాలు మూలాలుగా గల బహుపది సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x⁵ + 11x⁴ + x³ + 4x² – 13x + 6 = 0
కావలసిన సమీకరణం f(\(\frac{1}{x}\)) = 0
\(\frac{1}{x^5}+\frac{11}{x^4}+\frac{1}{x^3}+\frac{4}{x^2}-\frac{13}{x}+6=0\)
x⁵ చే గుణించగా
⇒ 1 + 11x + x² + 4x³ – 13x⁴ + 6x⁵ = 0
⇒ 6x⁵ – 13x⁴ + 4x³ + x² + 11x + 1 = 0

II.

ప్రశ్న 1.
x⁴ + x³ + 2x² + x + 1 = 0 సమీకరణ మూలాల వర్గాలు మూలాలుగా గల బహుపది సమీకరణాన్ని రూపొందించండి.
సాధన:
దత్త సమీకరణం f(x) = x⁴ + x³ + 2x² + x + 1 = 0
కావలసిన సమీకరణం f(√x) = 0
⇒ x² + x√x + 2x + √x + 1 = 0
⇒ √x(x + 1) = -(x² + 2x + 1)
వర్గం చేయగా
⇒ x(x + 1)² = (x² + 2x + 1)²
⇒ x(x² + 2x + 1) = x⁴ + 4x² + 1 + 4x³ + 4x + 2x²
⇒ x³ + 2x² + x = x⁴ + 4x³ + 6x² + 4x + 1
⇒ x⁴ + 3x³ + 4x² + 3x + 1 = 0

ప్రశ్న 2.
x³ + 3x² – 7x + 6 = 0 సమీకరణ మూలాల వర్గాలు మూలాలుగా గల బహుపది సమీకరణాన్ని రూపొందించండి.
సాధన:
దత్త సమీకరణం f(x) = x³ + 3x² – 7x + 6 = 0
కావలసిన సమీకరణం f(√x) = 0
⇒ x√x + 3x – 7√x + 6 = 0
⇒ √x(x – 7) = -(3x + 6)
వర్గం చేయగా
⇒ x(x – 7)² = (3x + 6)²
⇒ x(x² – 14x + 49) = 9x² + 36 + 36x
⇒ x³ – 14x² + 49x – 9x² – 36x – 36 = 0
⇒ x³ – 23x² + 13x – 36 = 0

ప్రశ్న 3.
x³ + 3x² + 2 = 0 సమీకరణ మూలాల ఘనాలు మూలాలుగా గల బహుపది సమీకరణాన్ని రూపొందించండి.
సాధన:
దత్త సమీకరణం x³ + 3x² + 2 = 0
y = x³ అయిన x = \(y^{1 / 3}\) అవుతుంది
∴ y + 3\(y^{2 / 3}\) + 2 = 0
3y\(y^{2 / 3}\) = -(y + 2)
ఘనం చేయగా
27y² = -(y + 2)³ = -(y³ + 6y² + 12y + 8)
∴ y³ + 6y² + 27y² + 12y + 8 = 0
⇒ y³ + 33y² + 12y + 8 = 0
కావలసిన సమీకరణం x³ + 33x² + 12x + 8 = 0

III.

ప్రశ్న 1.
-2 తో మార్పు చెందిన x⁴ – 5x³ + 7x² – 17x + 11 = 0 సమీకరణ మూలాల విలువలు మూలాలుగా గల బీజీయ సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x⁴ – 5x³ + 7x² – 17x + 11 = 0
కావలసిన సమీకరణం f(x + 2) = 0
⇒ (x + 2)⁴ – 5(x + 2)³ + 7(x + 2)² – 17(x + 2) + 11 = 0

కావలసిన సమీకరణం x⁴ + 3x³ + x² – 17x – 19 = 0

ప్రశ్న 2.
-3 తో మార్పు చెందిన x⁵ – 4x⁴ + 3x² – 4x + 6 = 0 సమీకరణ మూలాల విలువలు మూలాలుగా గల బహుపది సమీకరణాన్ని కనుక్కోండి. [T.S. Mar. ’16]
సాధన:
దత్త సమీకరణం f(x) = x⁵ – 4x⁴ + 3x² – 4x + 6 = 0
కావలసిన సమీకరణం f(x + 3) = 0
(x + 3)⁵ – 4(x + 3)³ + 3(x + 3)² – 4(x + 3) + 6 = 0

∴ కావలసిన సమీకరణం x⁵ + 11x⁴ + 42x³ + 57x² – 13x – 60 = 0

ప్రశ్న 3.
2 తో మార్పు చెందిన x⁴ – x³ – 10x² + 4x + 24 = 0 సమీకరణ మూలాల విలువలు మూలాలుగా గల బహుపది సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x⁴ – x³ – 10x² + 4x + 24 = 0
కావలసిన సమీకరణం f(x – 2) = 0
(x – 2)⁴ – (x – 2)³ – 10(x – 2)² + 4(x – 2) + 24 = 0

∴ కావలసిన సమీకరణం x⁴ – 9x³ + 20x² = 0

ప్రశ్న 4.
4తో మార్పు చెందిన 3x⁵ – 5x³ + 7 = 0 సమీకరణ మూలాల విలువలు మూలాలుగా గల బహువది సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = 3x⁵ – 5x³ + 7 = 0
కావలసిన సమీకరణం f(x – 4) = 0
3(x – 4)⁵ – 5(x – 4)³ + 7 = 0

∴ కావలసిన సమీకరణం 3x⁵ – 60x⁴ + 475x³ – 1860x² + 3600x – 2745 = 0

ప్రశ్న 5.
x యొక్క రెండో అత్యధిక ఘాత గుణకం సున్నా అయ్యే విధంగా కింది సమీకరణాలను పరివర్తన చేసి రూపాంతర సమీకరణాలను కనుక్కోండి.
(i) x³ – 6x² + 10x – 3 = 0
సాధన:
x యొక్క రెండో అత్యధిక ఘాత గుణకం లుప్తం అయ్యే విధంగా సమీకరణ మూలాలను \(\frac{-a_1}{n \cdot a_0}=\frac{-(-6)}{(3)(1)}\) = 2 తో మూలాల విలువలను పరివర్తనము చేయాలి.
అంటే f(x + 2) = 0 ను కనుక్కోవాలి.

∴ కావలసిన సమీకరణము x³ – 2x + 1 = 0

(ii) x⁴ + 4x³ + 2x² – 4x – 2 = 0
సాధన:
దత్త సమీకరణం x⁴ + 4x³ + 2x² – 4x – 2 = 0
మూలాలను h = \(-\frac{a_1}{n a_0}=\frac{-4}{4}\) = -1 తో మార్పు చెందించాలి.

∴ కావలసిన సమీకరణం x⁴ – 4x² + 1 = 0

(iii) x³ – 6x² + 4x – 7 = 0
సాధన:
దత్త సమీకరణం x³ – 6x² + 4x – 7 = 0
మూలాలను h = \(-\frac{a_1}{n a_0}=\frac{6}{3}\) = 2 తో మార్పు చెందించాలి.

∴ కావలసిన సమీకరణం x³ – 8x – 15 = 0

(iv) x³ + 6x² + 4x + 4 = 0
సాధన:
దత్త సమీకరణం x³ + 6x² + 4x + 4 = 0
రెండవ పదాన్ని లోపింపచేయటానికి మూలాలను h = \(-\frac{a_1}{n a_0}=-\frac{6}{3}\) = -2 కు మార్పు చెందించాలి.

∴ కావలసిన సమీకరణం x³ – 8x + 12 = 0

ప్రశ్న 6.
x యొక్క మూడో అత్యధిక ఘాత గుణకం సున్నా అయ్యే విధంగా కింది సమీకరణాలను పరివర్తన చేయండి.
(i) x⁴ + 2x³ – 12x² + 2x – 1 = 0
సాధన:
దత్త సమీకరణం
f(x) = x⁴ + 2x³ – 12x² + 2x – 1 = 0
x యొక్క మూడో అత్యధిక ఘాత గుణకం సున్నా కావాలి.
అంటే, దత్త సమీకరణ, మూలాలను h కు మార్పు చెందించాలి.
ఇచ్చట h అనేది \(f^{(4-3+1)}(h)\) = 0 ⇒ \(f^{(2)} \text { (h) }\) = 0 నుండి వస్తుంది.
f'(x) = 4x³ + 6x² – 24x + 2
f”(x) = 12x² + 12x – 24
f”(h) = 0
⇒ 12h² + 12h – 24 = 0
⇒ h² + h – 2 = 0
⇒(h + 2) (h – 1) = 0
⇒ h = -2 (లేదా) 1
సందర్భము (i):

∴ కావలసిన సమీకరణం x⁴ – 6x³ + 42x – 53 = 0
సందర్భము (ii):

కావలసిన సమీకరణము x⁴ + 6x³ – 12x – 8 = 0
∴ కావలసిన సమీకరణాలు x⁴ – 6x³ + 42x – 53 = 0 (లేదా) x⁴ + 6x³ – 12x – 8 = 0

(ii) x³ + 2x² + x + 1 = 0
సాధన:
f(x) = x³ + 2x² + x + 1 అనుకోండి.
x యొక్క మూడో అత్యధిక గుణకం సున్నా కావాలి అంటే, దత్త సమీకరణ మూలాలను ‘h’ తో మార్పు చెందించాలి.
ఇచ్చట h అనేది f'(h) = 0 నుండి వస్తుంది.
f'(x) = 3x² + 4x + 1
f'(h) = 0
⇒ 3h² + 4h + 1 = 0
⇒ (3h + 1) (h + 1) = 0
⇒ h = -1, \(-\frac{1}{3}\)
సందర్భము (i):

∴ కావలసిన సమీకరణం x³ – x² + 1 = 0
సందర్భము (ii):

∴ కావలసిన సమీకరణం x³ + x² + \(\frac{23}{27}\) = 0
⇒ 27x³ + 27x² + 23 = 0
∴ కావలసిన సమీకరణాలు x³ – x² + 1 = 0 (లేదా) 27x³ + 27x² + 23 = 0

ప్రశ్న 7.
కింది సమీకరణాలను సాధించండి.
(i) x⁴ – 10x³ + 26x² – 10x + 1 = 0
సాధన:
దత్త సమీకరణం ఒకటో కోవకు చెందిన సరిఘాత వ్యుత్కమ సమీకరణం
x² చే భాగించగా x² – 10x + 26 – \(\frac{10}{x}+\frac{1}{x^2}\) = 0
\([latex]\frac{10}{x}+\frac{1}{x^2}\)[/latex] …….(1)
a = x + \(\frac{1}{x}\) అనుకుంటే
\(x^2+\frac{1}{x^2}=\left(x-\frac{1}{x}\right)^2-2\) = a² – 2
(1) లో వ్రాయగా a² – 2 – 10a + 26 = 0
⇒ a² – 10a + 24 = 0
⇒ (a – 4) (a – 6) = 0
⇒ a = 4 (లేదా) 6
సందర్భము (i): a = 4
x + \(\frac{1}{x}\) = 4
⇒ x² + 1 = 4x
⇒ x² – 4x + 1 = 0
⇒ x = \(\frac{4 \pm \sqrt{16-4}}{2}=\frac{4 \pm 2 \sqrt{3}}{2}\)
⇒ x = 2 ± √3
సందర్భము (ii): a = 6 అయిన
x + \(\frac{1}{x}\) = 6
⇒ x² + 1 = 6x
⇒ x² – 6x + 1 = 0
⇒ x = \(\frac{6 \pm \sqrt{36-4}}{2}=\frac{6 \pm 4 \sqrt{2}}{2}\)
⇒ x = 3 ± 2√2
∴ దత్త సమీకరణానికి మూలాలు 3 ± 2√2, 2 ± √3

(ii) 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0 [A.P. Mar ’16, Mar. ’08, ’07]
సాధన:
f(x) = 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0
ఒకటవ కోవకు చెందిన బేసి తరగతి వ్యుత్కమ సమీకరణం
∴ -1 మూలం

f(x) ను (x + 1) చే భాగించగా
2x⁴ – x³ – 11x² – x + 2 = 0
x² చే భాగించగా
2x² – x – 11 – \(\frac{1}{x}+\frac{2}{x^2}\) = 0
\(2\left(x^2+\frac{1}{x^2}\right)-\left(x+\frac{1}{x}\right)-11=0\) ………(1)
a = x + \(\frac{1}{x}\) అయిన x² + \(\frac{1}{x^2}\) = a² – 2
(1) లో వ్రాయగా
2(a² – 2) – a – 11 = 0
⇒ 2a² – 4 – a – 11 = 0
⇒ 2a² – a – 15 = 0
⇒ (a – 3) (2a + 5) = 0
⇒ a = 3 లేదా \(\frac{-5}{2}\)
సందర్భము (i): a = 3 అయిన
x + \(\frac{1}{x}\) = 3
⇒ x² + 1 = 3x
⇒ x² – 3x + 1 = 0
⇒ x = \(\frac{3 \pm \sqrt{9-4}}{2}=\frac{3 \pm \sqrt{5}}{2}\)
సందర్భము (ii): a = \(\frac{-5}{2}\) అయిన
\(x+\frac{1}{x}=-\frac{5}{2}\)
⇒ \(\frac{x^2+1}{x}=-\frac{5}{2}\)
⇒ 2x² + 2 = -5x
⇒ 2x² + 5x + 2 = 0
⇒ (2x + 1) (x + 2) = 0
⇒ x = \(\frac{-1}{2}\), -2
∴ దత్త సమీకరణానికి మూలాలు -1, \(\frac{-1}{2}\), -2, \(\frac{3 \pm \sqrt{5}}{2}\)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 4 సమీకరణ వాదం Exercise 4(c) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 4 సమీకరణ వాదం Exercise 4(c)

అభ్యాసం – 4(సి)

I.

ప్రశ్న 1.
క్రింది మూలాలు గల బహుపది సమీకరణాలను రూపొందించండి.
(i) 2 + 3i, 2 – 3i, 1 + i, 1 – i
సాధన:
కావలసిన సమీకరణం [x – (2 + 3i)] [x – (2 – 3i)] [x – (1 + i)] [x – (1 – i)] = 0
⇒ [(x – 2) – 3i)] [(x – 2) + 3i] [(x – 1) – i] [(x – 1) + i] = 0
⇒ [(x – 2)² – 9i²] [(x – 1)² – i²] = 0
⇒ (x² – 4x + 4 + 9) (x² – 2x + 1 + 1) = 0
⇒ (x² – 4x + 13) (x² – 2x + 2) = 0
⇒ x⁴ – 4x³ + 13x² – 2x³ + 8x² – 26x + 2x² – 8x + 26 = 0
⇒ x⁴ – 6x³ + 23x² – 34x + 26 = 0

(ii) 3, 2, 1 + i, 1 – i
సాధన:
కావలసిన సమీకరణం (x – 3) (x – 2) [x – (1 + i)] [x – (1 – i)] = 0
⇒ (x² – 5x + 6) [(x – 1) – i] [(x – 1) + i) = 0
⇒ (x² – 5x + 6) [(x – 1)² – i²] = 0
⇒ (x² – 5x + 6) (x² – 2x + 1 + 1) = 0
⇒ (x² – 5x + 6) (x² – 2x + 2) = 0
⇒ x⁴ – 5x³ + 6x² – 2x³ + 10x² – 12x + 2x² – 10x + 12 = 0
⇒ x⁴ – 7x³ + 18x² – 22x + 12 = 0

(iii) 1 + i, 1 – i, -1 + i, -1 – i
సాధన:
కావలసిన సమీకరణం [x – (1 + i)] [x – (1 – i)] [x – (-1 + i)] [x – (-1 – i)] = 0
⇒ [(x – 1) – i] [(x – 1) + i] [(x + 1) – i] [(x + 1) + i) = 0
⇒ [(x – 1)² – i²] [(x + 1)² – i²] = 0
⇒ (x² – 2x + 1 + 1) (x² + 2x + 1 + 1) = 0
⇒ (x² – 2x + 2) (x² + 2x + 2) = 0
⇒ x⁴ – 2x³ + 2x² + 2x³ – 4x² + 4x + 2x² – 4x + 4 = 0
⇒ x⁴ + 4 = 0

(iv) 1 + i, 1 – i, 1 + i, 1 – i
సాధన:
కావలసిన సమీకరణం [x – (1 + i)] [x – (1 – i)]
⇒ [x – (1 + i)] [x – (1 – i)] = 0
⇒ [(x – 1) – i]² [(x – 1) + i]² = 0
⇒ [(x – 1)² – i²] = 0
⇒ (x² – 2x + 1 + 1)² = 0
⇒ x⁴ + 4x² + 4 – 4x³ + 4x² – 8x = 0
⇒ x⁴ – 4x³ + 8x² – 8x + 4 = 0

ప్రశ్న 2.
కింది మూలాలు గల అకరణీయ గుణకాలు గల బహుపది సమీకరణాన్ని రూపొందించండి.
(i) 4√3, 5 + 2i
సాధన:
బహుపది సమీకరణ గుణకాలు అకరణీయ సంఖ్యలైన, దాని మూలాలు సంయుగ్మ కరణులు మరియు సంయుగ్మసంకీర్ణ సంఖ్యలు.
α = 4√3 అయిన β = -4√3 మరియు γ = 5 + 2i అయిన δ = 5 – 2i
α, β, γ, δ లు మూలాలు
α + β = 0, αβ = -48
γ + δ = 10, γδ = 25 + 4 = 29
కావలసిన సమీకరణం [x² – (α + β)x + αβ] [x² – (γ + δ)x + γδ] = 0
⇒ (x² – 48) (x² – 10x + 29) = 0
⇒ x⁴ – 10x³ + 29x² – 48x² + 480x – 1932 = 0
⇒ x⁴ – 10x³ – 19x² + 480x – 1932 = 0

(ii) 1 + 5i, 5 – i
సాధన:
బహుపది సమీకరణ గుణకాలు అకరణీయ సంఖ్యలైన, దాని మూలాలు సంయుగ్మ కరణులు మరియు సంయుగ్మసంకీర్ణ సంఖ్యలు.
α = 1 + 5i అయిన β = 1 – 5i
మరియు γ = 5 + i అయిన δ = 5 – i లు మూలాలు.
α + β = 2, αβ = 26
γ + δ = 10, γδ = 26
కావలసిన సమీకరణం [x² – (α + β)x + αβ] [x² – (γ + δ)x + γδ] = 0
⇒ (x² – 2x + 26) (x² – 10x + 26) = 0
⇒ x⁴ – 12x³ + 72x² – 312x + 676 = 0

(iii) i – √5
సాధన:
బహుపది సమీకరణ గుణకాలు అకరణీయ సంఖ్యలైన, దాని మూలాలు సంయుగ్మ కరణులు మరియు సంయుగ్మసంకీర్ణ సంఖ్యలు.
α = i – √5, β = i + √5, γ = -i – √5, δ = -i + √5 లు మూలాలు
α + β = 2i, αβ = -6
γ + δ = -2i, γδ = -6
కావలసిన సమీకరణం [x² – (α + β)x + αβ] [x² – (γ + δ)x + γδ] = 0
⇒ (x² – 2ix – 6) (x² + 2ix – 6) = 0
⇒ [(x² – 6) – 2ix] [(x² – 6) + 2ix] = 0
⇒ (x² – 6)² + 4x² = 0
⇒ x⁴ + 36 – 12x² + 4×2 = 0
⇒ x⁴ – 8x² + 36 = 0

(iv) -√3 + i√2
సాధన:
α = -√3 + i√2, β = -√3 – i√2, γ = √3 – i√2, δ = √3 + i√2 లు మూలాలు
α + β = -2√3
αβ = (-√3)² – (i√2)²
= 3 – i² (2)
= 5
γ + δ = 2√3, γδ = 5
కావలసిన సమీకరణము [x² – (α + β)x + αβ] [x² – (γ + δ)x + γδ] = 0
⇒ (x² + 2√3x + 5) (x² – 2√3x + 5) = 0
⇒ (x² + 5)² – (2√3x)² = 0
⇒ x⁴ + 25 + 10x² – 12x² = 0
⇒ x⁴ – 2x² + 25 = 0

II.

ప్రశ్న 1.
x⁴ + 2x³ – 5x² + 6x + 2 = సమీకరణపు ఒక మూలం 1 + i అయిన, సమీకరణాన్ని సాధించండి.
సాధన:
1 + i ఒక మూలం ⇒ 1 – i ఇంకొక మూలం అవుతుంది.
1 ± i మూలాలుగా గల సమీకరణం
x² – 2x + 2 = 0
∴ x² – 2x + 2 ఒక కారణాంకము
x⁴ + 2x³ – 5x² + 6x + 2 = 0

x = -2 ± √3
∴ మూలాలు 1 ± i, -2 ± √3

ప్రశ్న 2.
3x³ – 4x² + x + 88 = 0 సమీకరణపు ఒక మూలం 2 – √-7 అయిన, సమీకరణాన్ని సాధించండి.
సాధన:
2 – √-7 ⇒ 2 – √7i ఒక మూలం
⇒2 + √7i ఇంకొక మూలం
2 ± √7i మూలాలుగా గల సమీకరణం x² – 4x + 11 = 0
∴ x² – 4x + 11 దత్త సమీకరణానికి ఒక కారణాంకము

3x + 8 = 0
⇒ x = \(\frac{-8}{3}\)
∴ దత్త సమీకరణానికి మూలాలు 2 ± √7i, \(\frac{-8}{3}\)

ప్రశ్న 3.
x⁴ – 4x² + 8x + 35 = 0 సమీకరణపు ఒక మూలం 2 + i√3 అయితే, సమీకరణాన్ని సాధించండి.
సాధన:
2 + i√3 ఒక మూలం ⇒ 2 – i√3 ఇంకొక మూలం
2 ± i√3 మూలాలుగాగల సమీకరణం x² – 4x + 7 = 0
∴ x² – 4x + 7 దత్త సమీకరణానికి ఒక మూలం
x⁴ – 4x² + 8x + 35

∴ దత్త సమీకరణానికి మూలాలు 2 ± i√3, -2 ± i

ప్రశ్న 4.
x⁴ – 6x³ + 11x² – 10x + 2 = 0 సమీకరణపు ఒక మూలం 2 + √3 అయితే, సమీకరణాన్ని సాధించండి.
సాధన:
2 + √3 ఒక మూలం ⇒ 2 – √3 ఇంకొక మూలం.
2 ± √3 మూలాలుగాగల సమీకరణం x² – 4x + 1 = 0
∴ x² – 4x + 1 ఒక కారణాంకము
x⁴ – 6x³ + 11x² – 10x + 2 = 0

∴ దత్త సమీకరణానికి 2 ± √3, 1 ± i

ప్రశ్న 5.
x⁴ + 2x² – 16x + 77 = 0 సమీకరణపు ఒక మూలం -2 + √-7 అయితే, సమీకరణాన్ని పూర్తిగా సాధించండి.
సాధన:
-2 – √-7 (i.e.) -2 + i√7 ఒక మూలం.
⇒ -2 – i√7 ఇంకొక మూలం -2 + i√7
-2 ± i√7 మూలాలుగా గల సమీకరణం x² + 4x + 11 = 0
∴ x² + 4x + 11 ఒక కారణాంకము
x⁴ + 2x² – 16x + 77 = 0

∴ దత్త సమీకరణానికి మూలాలు -2 ± i√7, 2 ± √3i

ప్రశ్న 6.
x⁴ + 2x³ – 16x² – 22x + 7 = 0 సమీకరణపు ఒక మూలం 2 – √3 అయితే, సమీకరణాన్ని సాధించండి.
సాధన:
2 – √3 ఒక మూలం ⇒ 2 + √3 ఇంకొక మూలం
2 ± √3 లు మూలాలుగా గల వర్గ సమీకరణం
x² – (2 + √3 + 2 – √3)x + (2 + √3) (2 – √3) = 0
⇒ x² – 4x + 1 = 0

∴ దత్త సమీకరణానికి మూలాలు 2 ± √3, -3 ± √2

ప్రశ్న 7.
3x⁵ – 4x⁴ – 42x³ + 56x² + 27x – 36 = 0 సమీకరణానికి ఒక మూలం √2 + √5 అయితే, సమీక రణాన్ని సాధించండి.
సాధన:
√2 + √5 ఒక మూలం
⇒ √2 – √5, -√2 + √5, -√2 – √5 లు కూడా దత్తసమీకరణానికి మూలాలు.
√2 ± √5 మూలాలుగా గల వర్గ సమీకరణం
x² – (√2 + √5 + √2 – √5)x + (√2 + √5) (√2 – √5) = 0
⇒ x² – 2√2x – 3 = 0
-√2 ± √5 లు మూలాలుగా గల వర్గ సమీకరణం
x² – (-√2 + √5 – √2 – √5)x + (-√2 + √5)(-√2 – √5) = 0
⇒ x² + 2√2x – 3 = 0
±√2±√5 లు మూలాలుగా గల సమీకరణం
(x² + 2√2x – 3) (x² – 2√2x – 3) = 0
⇒ (x² – 3)² – (2√2x)² = 0
⇒ x⁴ – 6x² + 9 – 8×2 = 0
⇒ x⁴ – 14x² + 9 = 0
3x⁵ – 4x⁴ – 42x³ + 56x² + 27x – 36 = 0
⇒ 3x(x⁴ – 14x² + 9) – 4(x⁴ – 14x² + 9) = 0
⇒ (x⁴ – 14x² + 9) (3x – 4) = 0
⇒ x = ±√2 ± √5 లేదా \(\frac{4}{3}\)
∴ దత్త సమీకరణానికి మూలాలు ±√2 ± √5, \(\frac{4}{3}\)

ప్రశ్న 8.
x⁴ – 9x³ + 27x² – 29x + 6 = 0 సమీకరణపు ఒక మూలం 2 – √3 అయితే, సమీకరణాన్ని సాధించండి.
సాధన:
2 – √3 ఒక మూలం ⇒ 2 + √3 ఇంకొక మూలం.
2 ± √3 లు మూలాలుగా గల సమీకరణం
x² – 4x + 1 = 0
∴ x² – 4x + 1 ఒక కారణాంకము

x² – 5x + 6 = 0
⇒ (x – 2) (x – 3) = 0
⇒ x = 2, 3
∴ దత్త సమీకరణానికి మూలాలు 2 ± √3, 2, 3

ప్రశ్న 9.
a, b, c…. k, m, a’, b’, c’….k’ లు అన్నీ వాస్తవ సంఖ్యలైనపుడు \(\frac{a^2}{x-a^{\prime}}+\frac{b^2}{x-b^{\prime}}+\frac{c^2}{x-c^{\prime}}\) +…..+ \(\frac{k^2}{x-k^{\prime}}\) = m సమీకరణం వాస్తవేతర మూలాన్ని కలిగి ఉండదని చూపండి.
సాధన:
దత్త సమీకరణానికి α + iβ ఒక మూలం అనుకోండి.
β ≠ 0 అనుకుందాం.
అపుడు α – iβ కూడా దత్త సమీకరణానికి మూలం అవుతుంది.
దత్త సమీకరణంలో α + iβ వ్రాయగా

= 0
⇒ β = 0
ఇది అనుకొన్నదానికి విరుద్ధం.
∴ దత్త సమీకరణానికి వాస్తవేతర మూలాలు ఉండవు.