Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(a)

I.

Question 1.
ఈ క్రింది వాటిని సూక్ష్మీకరించండి.
(i) tan(θ – 14π)
Solution:
tan(θ – 14π) = tan(14π – θ)
= tan(2 . (7π) – θ)
= tan θ

(ii) cot(\(\frac{21 \pi}{2}\) – θ)
Solution:
cot(\(\frac{21 \pi}{2}\) – θ) = cot(10π + (\(\frac{\pi}{2}\) – θ))
= cot(\(\frac{\pi}{2}\) – θ)
= tan θ

(iii) cosec(5π + θ)
Solution:
cosec(5π + θ) = cosec(2π + (3π + θ))
= cosec(3π + θ)
= cosec(2π + (π + θ))
= cosec (π + θ)
= -cosec θ

(iv) sec(4π – θ)
Solution:
sec(4π – θ) = sec(2π + (2π – θ))
= sec (2π – θ)
= sec θ

Question 2.
క్రింది వాటి విలువలు కనుక్కోండి.
(i) sin(-405°)
Solution:
sin (-405°) = sin(360° + 45°)
= -sin 45°
= \(-\frac{1}{\sqrt{2}}\)

(ii) cos(\(-\frac{7 \pi}{2}\))
Solution:
cos(\(-\frac{7 \pi}{2}\)) = -cos(\(\frac{7 \pi}{2}\))
= cos 630°
= cos (360° + 270°)
= -cos 270°
= cos(180° + 90°)
= -cos 90°
= 0

(iii) sec(2100°)
Solution:
sec(2100°) = sec (5 × 360° + 300°)
= sec 300°
= sec(360° – 60°)
= sec 60°
= 2

(iv) cot(-315°)
Solution:
cot(-315°) = -cot 315°
= cot(360° – 45°)
= -cot 45°
= 1

Question 3.
కింది వాటిని గణించండి.
(i) cos²45° + cos²135° + cos²225° + cos²315°
Solution:
cos²45° + cos²135° + cos²225° + cos²315°

(ii) \(\sin ^2 \frac{2 \pi}{3}+\cos ^2 \frac{5 \pi}{6}-\tan ^2 \frac{3 \pi}{4}\)
Solution:
\(\sin ^2 \frac{2 \pi}{3}+\cos ^2 \frac{5 \pi}{6}-\tan ^2 \frac{3 \pi}{4}\)

(iii) cos 225° – sin 225° + tan 495° – cot 495°
Solution:
cos(180° + 45°) – sin(180° + 45°) + tan(360° + 135°) – cot(360° + 135°)
= -cos 45° + sin 45° – tan 135° + cot 135°
= \(-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\) + 1 – 1
= 0

(iv) (a) θ = \(\frac{7 \pi}{4}\), (b) θ = \(\frac{11 \pi}{3}\) అయినప్పుడు (cos θ – sin θ) ల విలువ.
Solution:

Question 4.
(i) కోణం θ మూడో పాదంలో లేదు, sin θ = \(\frac{-1}{3}\) అయితే (a) cos θ (b) cot θ ల విలువలు కనుక్కోండి. [Mar. ’13]
Solution:
∵ sin θ = \(\frac{-1}{3}\), sin θ ఋణాత్మకం.
θ మూడవ పాదంలో లేదు.
⇒ θ నాల్గవ పాదంలో ఉంటుంది.
∴ నాల్గవ పాదంలో cos θ +ve, cot θ -ve.

(ii) కోణం θ ఒకటో పాదం లో లేదు, cos θ = t (0 < t < 1) అయితే (a) sin θ (b) tan θ విలువలను కనుక్కోండి.
Solution:
cos θ = t, (0 < t < 1)
⇒ cos θ ధనాత్మకం
θ ఒకటవ పాదంలో లేదు.
⇒ θ నాల్గవ పాదంలో ఉంటుంది.

(iii) sin 330° cos 120° + cos 210° sin 300° విలువను కనుక్కోండి.
Solution:
sin 330° cos 120° + cos 210° sin 300°
= sin(360° – 30°) . cos(180° – 60°) + cos(180° + 30°) . sin(360° – 60°)
= (-sin 30°) (-cos 60°) + (-cos 30°) (-sin 60°)
= sin 30° cos 60° + cos 30° sin 60°
= sin(30° + 60°) [∵ sin A cos B + cos A sin B = sin (A + B)]
= sin(90°)
= 1

(iv) cosec θ + cot θ = \(\frac{1}{3}\), అయితే, cos θ ను కనుక్కొని θ ఏ పాదంలో ఉందో నిర్థారించండి.
Solution:
∵ cosec θ + cot θ = \(\frac{1}{3}\)
cosec θ – cot θ = 3 (∵cosec²θ – cot²θ = 1)

Question 5.
(i) sin α + cosec α = 2, n ∈ z అయితే sinⁿα + cosecⁿα విలువను కనుక్కోండి. [May ’13]
Solution:
ఇచ్చినది sin α + cosec α = 2
S.B.S.
sin²α + cosec²α + 2 = 4
sin²α + cosec²α = 2
sin α + cosec α = 2
C.B.S.
sin³α + cosec³α + 3 sin α . cosec α (sin α + cosec α) = 8
sin³α + cosec³α + 3(2) = 8
sin³α + cosec³α = 8 – 6
sin³α + cosec³α = 2
similarly sinⁿα + cosecⁿα = 2

(ii) sec θ + tan θ = 5 అయితే, θ ఉండే పాదాన్ని, sin θ విలువను కనుక్కోండి.
Solution:

II.

Question 1.
కింది వాటిని నిరూపించండి.
(i) \(\frac{\cos (\pi-A) \cdot \cot \left(\frac{\pi}{2}+A\right) \cos (-A)}{\tan (\pi+A) \tan \left[\frac{3 \pi}{2}+A\right] \sin (2 \pi-A)}\)
Solution:
\(\frac{\cos (\pi-A) \cdot \cot \left(\frac{\pi}{2}+A\right) \cos (-A)}{\tan (\pi+A) \tan \left[\frac{3 \pi}{2}+A\right] \sin (2 \pi-A)}\)
= \(\frac{-\cos A(-\tan A) \cos A}{\tan A(-\cot A)\left(-\sin ^{\prime} A\right)}\)
= cos A

(ii) \(\frac{\sin (3 \pi-A) \cos \left(A-\frac{\pi}{2}\right) \tan \left(\frac{3 \pi}{2}-A\right)}{{cosec}\left(\frac{13 \pi}{2}+A\right) \sec (3 \pi+A) \cot \left(A-\frac{\pi}{2}\right)}\) = cos4A
Solution:
\(\frac{\sin (3 \pi-A) \cos \left(A-\frac{\pi}{2}\right) \tan \left(\frac{3 \pi}{2}-A\right)}{{cosec}\left(\frac{13 \pi}{2}+A\right) \sec (3 \pi+A) \cot \left(A-\frac{\pi}{2}\right)}\)

(iii) sin 780° . sin 480° + cos 240° . cos 300° = \(\frac{1}{2}\)
Solution:
sin 780° . sin 480° + cos 240° . cos 300°
= sin(2(360°) + 60°) . sin(360° + 120°) + cos(270° – 30°) . cos(360° – 60°)
= sin 60° . sin 120° – sin 30° cos 60°

(iv) \(\frac{\sin 150^{\circ}-5 \cos 300^{\circ}+7 \tan 225^{\circ}}{\tan 135^{\circ}+3 \sin 210^{\circ}}\) = -2
Solution:
\(\frac{\sin 150^{\circ}-5 \cos 300^{\circ}+7 \tan 225^{\circ}}{\tan 135^{\circ}+3 \sin 210^{\circ}}\)

(v) \(\cot \left(\frac{\pi}{20}\right) \cdot \cot \left(\frac{3 \pi}{20}\right) \cdot \cot \left(\frac{5 \pi}{20}\right) \cdot \cot \left(\frac{7 \pi}{20}\right)\) . \(\cot \left(\frac{9 \pi}{20}\right)\) = 1
Solution:
L.H.S = \(\cot \left(\frac{\pi}{20}\right) \cdot \cot \left(\frac{3 \pi}{20}\right) \cdot \cot \left(\frac{5 \pi}{20}\right) \cdot \cot \left(\frac{7 \pi}{20}\right)\) . \(\cot \left(\frac{9 \pi}{20}\right)\)
= cot(9°) cot(27°) cot(45°) cot(63°) cot(81°)
= cot(9°) cot(27°) (1) cot(90° – 27°) cot(90° – 9°)
= cot(9°) cot(27°) tan 27° tan 9°
= (tan 9° cot 9°) (tan 27° cot 27°)
= (1) (1)
= 1

Question 2.
(i) \(\frac{\sin \left(-\frac{11 \pi}{3}\right) \tan \left(\frac{35 \pi}{6}\right) \sec \left(-\frac{7 \pi}{3}\right)}{\cot \left(\frac{5 \pi}{4}\right) {cosec}\left(\frac{7 \pi}{4}\right) \cos \left(\frac{17 \pi}{6}\right)}\) ను సూక్ష్మీకరించండి.
Solution:
sin(\(\frac{-11 \pi}{3}\))
= sin(-660°)
= sin(-2 × 360° + 60°)
= sin 60°
= \(\frac{\sqrt{3}}{2}\)
tan(\(\frac{35 \pi}{6}\))
= tan(1050°)
= tan(3 × 360° – 30°)
= -tan 30°
= \(-\frac{1}{\sqrt{3}}\)
sec(\(-\frac{7 \pi}{3}\))
= sec(-420°)
= sec 420°
= sec(360° + 60°)
= sec 60°
= 2
cot(\(\frac{5 \pi}{4}\))
= cot(225°)
= cot(180° + 45°)
= cot 45°
= 1
cosec(\(\frac{7 \pi}{4}\))
= cosec(315°)
= cosec(270° + 45°)
= -sec 45°
= -√2
cos(\(\frac{17 \pi}{6}\))
= cos(570°)
= cos(540° – 30°)
= -cos 30°
= \(-\frac{\sqrt{3}}{2}\)

(ii) tan 20° = p అయితే, \(\frac{\tan 610^{\circ}+\tan 700^{\circ}}{\tan 560^{\circ}-\tan 470^{\circ}}=\frac{1-p^2}{1+p^2}\) అని చూపండి.
Solution:

Question 2.
α, β లు పూరక కోణాలు. b sin α = a, అయితే, sin α cos β – cos α sin β విలువను కనుక్కోండి.
Solution:
∵ α, β లు పూరక కోణాలు.
α + β = 90°
⇒ β = 90° – α
sin α cos β – cos α sin β = sin(α – β)
= sin[(α – (90° – α)]
= sin[2α – 90°]
= -sin(90° – 2α)
= -cos 2α
= -(1 – 2 sin²α) (∵ cos 2α = 1 – 2 sin²α)
= -1 + 2\(\left(\frac{a}{b}\right)^2\) [∵ sin α = \(\frac{a}{b}\) (ఇవ్వబడినది)]
= \(\frac{-b^2+2 a^2}{b^2}\)
= \(\frac{2 a^2-b^2}{b^2}\)

Question 3.
(i) A రెండో పాదం లేని కోణం, B మూడవ పాదంలో లేని కోణం, cos A = cos B = \(-\frac{1}{2}\) అయితే, \(\frac{4 \sin B-3 \tan A}{\tan B+\sin A}\) విలువను కనుక్కోండి.
Solution:
Solution:
∵ cos A = \(-\frac{1}{2}\), A రెండవ పాదంలో లేదు.
cos A -ve, కనుక
⇒ A, మూడవ పాదంలో ఉంటుంది.
cos B = \(-\frac{1}{2}\), B మూడవ పాదంలో లేదు.
cos B -ve, కనుక
⇒ B, రెండవ పాదంలో ఉంటుంది.
∵ cos A = \(-\frac{1}{2}\)
A మూడవ పాదంలో ఉంటుంది.
⇒ A = 240°
∵ cos B = \(-\frac{1}{2}\), B రెండవ పాదంలో ఉంది.
⇒ B = 120°

(ii) కోణాలు A, B లు 4వ పాదంలో లేవు, 8 tan A = -15, 25 sin B = -7 అయితే, sin A cos B + cos A sin B = \(\frac{-304}{425}\) అని చూపండి.
Solution:
8 tan A = -15 ⇒ tan A = \(\frac{-15}{8}\)
25 sin B = -7 ⇒ sin B = \(\frac{-7}{25}\)
దత్తాంశము గురించి A, Bలు నాలుగో పాదంలో ఉండవు.
∴ A రెండవ పాదంలోను B మూడవ పాదంలో ఉండాలి.
sin A cos B + cos A sin B =

(iii) A, B, C, D లు ఒక చక్రీయ చతుర్భుజం కోణాలు అయితే,
(a) sin A – sin C = sin D – sin B
(b) cos A + cos B + cos C + cos D = 0 అని చూపండి.
Solution:
∵ A, B, C, D లు చక్రీయ చతుర్భుజ కోణాలు,
⇒ A + C = 180°, B + D = 180°
⇒ C = 180° – A, D = 180° – B
(i) L.H.S. = sin A – sin C
= sin (A) – sin (180° – A)
= sin A – sin A
= 0
R.H.S. = sin D – sin B
= sin (180° – B) – sin B
= sin B – sin B
= 0
∴ L.H.S. = R.H.S.
i.e., sin A – sin C = sin D – sin B
(ii) L.H.S. = cos A + cos B + cos C + cos D
= cos A + cos B + cos (180° – A) + cos (180° – B)
= cos A + cos B – cos A – cos B
= 0
∴ cos A + cos B + cos C + cos D = 0

Question 4.
(i) a cos θ – b sin θ = c, a sin θ + b cos θ = \(\pm \sqrt{a^2+b^2-c^2}\) అని చూపండి.
Solution:
a cos θ – b sin θ = c
let a sin θ + b cos θ = x
వర్గము చేసి కూడగా
(a cos θ – b sin θ)² + (a sin θ + b cos θ)² = c² + x²
⇒ a² cos²θ + b² sin²θ – 2ab sin θ cos θ + a² sin²θ + b² cos²θ + 2ab sin θ = c² + x²
⇒ a² + b² = c² + x²
⇒ a² + b² – c² = x²
⇒ x = \(\pm \sqrt{a^2+b^2-c^2}\)
∴ a sin θ + b cos θ = \(\pm \sqrt{a^2+b^2-c^2}\)

(ii) 3 sin A + 5 cos A = 5, అయితే 5 sin A – 3 cos A = ±3 అని చూపండి.
Solution:
3 sin A + 5 cos A = 5
let 5 sec A – 3 cos A = x
ఇరువైపులా వర్గము చేసి కూడగా
(3 sin A + 5 cos A)² + (5 sin A – 3 cos A)² = 5² + x²
⇒ 9 sin²A + 25 cos²A + 30 sin A cos A + 25 sin²A + 9 cos²A – 30 sin A cos A = 25 + x²
⇒ 9 + 25 = 25 + x²
⇒ x² = 9
⇒ x = ±3
∴ 5 sin A – 3 cos A = ±3

(iii) tan²θ = (1 – e²), అయితే sec θ + tan³θ . cosec θ = \(\left(2-e^2\right)^{3 / 2}\) అని చూపండి.
Solution:
tan²θ = 1 – e²
sec²θ = 1 + tan²θ = 2 – e²
sec θ + tan³θ . cosec θ
= sec θ + \(\frac{\sin ^3 \theta}{\cos ^3 \theta} \cdot \frac{1}{\sin \theta}\)
= sec θ + \(\frac{\sin ^2 \theta}{\cos ^2 \theta} \cdot \frac{1}{\cos \theta}\)
= sec θ + tan²θ . sec θ
= sec θ (1 + tan²θ)
= sec θ . sec²θ
= \(\left(2-e^2\right) \sqrt{2-e^2}\)
= \(\left(2-e^2\right)^{3 / 2}\)

III.

Question 1.
కింది వాటిని నిరూపించండి.
(i) \(\frac{\tan \theta+\sec \theta-1}{\tan \theta-\sec \theta+1}=\frac{1+\sin \theta}{\cos \theta}\) [Mar. ’14]
Solution:

(ii) (1 + cot θ – cosec θ) (1 + tan θ + sec θ) = 2
Solution:
L.H.S. = (1 + cot θ – cosec θ) (1 + tan θ + sec θ)

(iii) 3(sin θ – cos θ)⁴ + 6(sin θ + cos θ)² + 4(sin⁶θ + cos⁶θ) = 13
Solution:
(sin θ – cos θ)² = sin²θ + cos²θ – 2 sin θ . cos θ = 1 – 2 sin θ cos θ
(sin θ – cos θ)⁴ = (1 – 2 sin θ cos θ)² = 1 + 4 sin²θ cos²θ – 4 sin θ cos θ …….(1)
(sin θ + cos θ)² = sin²θ + cos²θ + 2 sin θ cos θ = 1 + 2 sin θ cos θ ……(2)
sin⁶θ + cos⁶θ = (sin²θ + cos²θ)³ – 3 sin²θ cos²θ (sin²θ + cos²θ) = 1 – 3 sin²θ cos²θ …….(3)
L.H.S. = 3(1 + 4 sin²θ cos²θ – 4 sin θ cos θ) + 6(1 + 2 sin θ cos θ) + 4(1 – 3 sin²θ cos²θ)
= 3 + 12 sin²θ cos²θ – 12 sin θ cos θ + 6 + 12 sin θ cos θ + 4 – 12 sin²θ cos²θ
= 3 + 6 + 4
= 13
= R.H.S.

Question 2.
కింది వాటిని నిరూపించండి.
(i) (sin θ + cosec θ)² + (cos θ + sec θ)² – (tan²θ + cot²θ) = 7
Solution:
L.H.S. = (sin θ + cosec θ)² + (cos θ + sec θ)² – (tan²θ + cot²θ)
= (sin²θ + cosec²θ + 2 sin θ cosec θ) + (cos²θ + sec²θ + 2 cos θ sec θ – (tan²θ + cot²θ)
= (sin²θ + cos²θ) + (1 + cot²θ) + (1 + tan²θ) + 4 – tan²θ – cot²θ
= 1 + 1 + 1 + 4
= 7

(ii) cos⁴α + 2 cos²α \(\left(1-\frac{1}{\sec ^2 \alpha}\right)\) = (1 – sin⁴α)
Solution:
L.H.S. = cos⁴α + 2 cos²α \(\left(1-\frac{1}{\sec ^2 \alpha}\right)\)
= cos⁴α + 2 cos²α (1 – cos²α)
= cos²α [cos²α + 2 sin²α]
= (1 – sin²α) [cos²α + sin²α + sin²α]
= (1 – sin²α) (1 + sin²α)
= 1 – sin⁴α

(iii) \(\frac{(1+\sin \theta-\cos \theta)^2}{(1+\sin \theta+\cos \theta)^2}=\frac{1-\cos \theta}{1+\cos \theta}\)
Solution:

(iv) \(\frac{2 \sin \theta}{(1+\cos \theta+\sin \theta)}\) = x అయితే, \(\frac{(1-\cos \theta+\sin \theta)}{(1+\sin \theta)}\) విలువను కనుక్కోండి.
Solution:

Question 3.
కింది వాటిలో θను లోపింపచేయండి.
(i) x = a cos³θ; y = b sin³θ
Solution:

(ii) x = a cos⁴θ; y = b sin⁴θ
Solution:

(iii) x = a(sec θ + tan θ); y = b(sec θ – tan θ)
Solution:
\(\frac{x}{a}\) = sec θ + tan θ
\(\frac{y}{b}\) = sec θ – tan θ
\(\frac{x}{a} \times \frac{y}{b}\) = (sec θ + tan θ) (sec θ – tan θ) = sec²θ – tan²θ
\(\frac{xy}{ab}\) = 1
xy = ab

(iv) x = cot θ + tan θ; y = sec θ – cos θ
Solution:
ఇచ్చినది x = cot θ + tan θ, y = sec θ – cos θ
x² = (cot θ + tan θ)²
= cot²θ + tan²θ + 2 cot θ tan θ
= cot²θ + tan²θ + 2(1)
= (1 + tan²θ) + (1 + cot²θ)
= sec²θ + cosec²θ
= \(\frac{1}{\cos ^2 \theta}+\frac{1}{\sin ^2 \theta}\)
= \(\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin ^2 \theta \cos ^2 \theta}\)
= \(\frac{1}{\sin ^2 \theta \cos ^2 \theta}\)
∴ x² = sec²θ cosec²θ ……..(1)
y = (sec θ – cos θ)
y² = (sec θ – cos θ)²
y² = sec²θ + cos²θ – 2(sec θ cos θ)
= sec²θ + cos²θ – 2(1)
= (sec²θ – 1) – (1 – cos²θ)
= tan²θ – sin²θ
= sin²θ \(\left(\frac{1}{\cos ^2 \theta}-1\right)\)
= sin²θ (sec²θ – 1)
= sin²θ tan²θ ……..(2)
ఇప్పుడు x²y = (sec²θ cosec²θ) (sin θ tan θ)

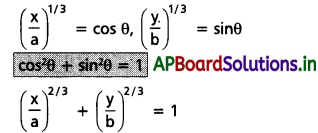
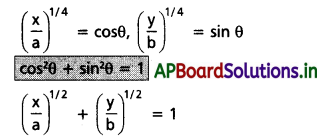
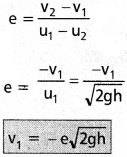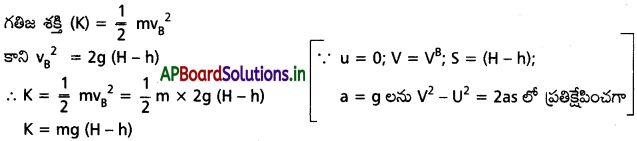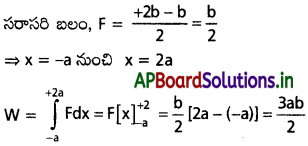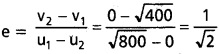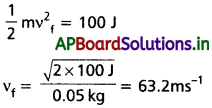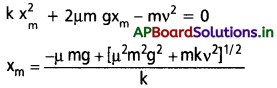Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 6th Lesson పని, శక్తి, సామర్ధ్యం Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 6th Lesson పని, శక్తి, సామర్ధ్యం

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
బలం వల్ల పని జరగని పరిస్థితులను తెలపండి.
జవాబు:

1. స్థానభ్రంశం శూన్యం అయినపుడు
2. బలదిశకు స్థానభ్రంశం లంబంగా ఉన్నప్పుడు
3. ఒక వస్తువు సంవృత పథంలో నిత్యత్వ బలం వల్ల చలించుట వల్ల జరుగు పని శూన్యం.

ప్రశ్న 2.
పని, సామర్థ్యం, శక్తులను నిర్వచించండి. వాటి S.I. ప్రమాణాలు తెలియచేయండి.
జవాబు:
పని :
బల ప్రయోగం వల్ల వస్తువు స్థానభ్రంశం పొందితే ఆ బలం పని చేసిందని అంటారు. i.e., W = \(\overrightarrow{F}.\overrightarrow{S}\) = F S cos θ.
S.I. ప్రమాణం : జౌల్
సామర్థ్యం : పని జరిగే రేటును సామర్థ్యం అంటారు.
S.I. ప్రమాణం : జౌల్ / సె లేక వాట్
శక్తి : పని చేసే దారుఢ్యాని శక్తి అంటారు.
S.I. ప్రమాణం : జౌల్.

ప్రశ్న 3.
గతిజ శక్తి, ద్రవ్యవేగాల మధ్య సంబంధాన్ని తెలియచేయండి.
జవాబు:
గతిజ శక్తి E_k = \(\frac{P^2}{2m}\) ; ఇక్కడ P = వస్తు ద్రవ్యవేగము.
m = వస్తు ద్రవ్యరాశి.

ప్రశ్న 4.
కింది సందర్భాల్లో బలం చేసిన పని సంజ్ఞను తెలియచేయండి.
a) బకెట్ను బిగించిన తాడు సహాయంతో బావిలో నుంచి బకెట్ను తీసే సందర్భంలో మనిషి చేసిన పని.
b) పై సందర్భంలో గురుత్వ బలం చేసిన పని.
జవాబు:
a) చేసిన పని ధనాత్మకము
b) గురుత్వ బలం చేసిన పని ఋణాత్మకము.

ప్రశ్న 5.
కింది సందర్భాల్లో ఒక బలం చేసిన పని సంజ్ఞను తెలియచేయండి.
a) ఒక వస్తువు వాలు తలంపై కిందికి జారుతున్నప్పుడు ఘర్షణ చేసిన పని.
b) పై సందర్భంలో గురుత్వ బలం చేసిన పని.
జవాబు:
a) ఘర్షణ చేసే పని ఋణాత్మకము
b) గురుత్వ బలం చేసిన పని ధనాత్మకము.

ప్రశ్న 6.
కింది సందర్భాల్లో ఒక బలం చేసిన పని సంజ్ఞను తెలియచేయండి.
a) ఒక వస్తువు సమవేగంతో ఘర్షణ ఉన్న క్షితిజ సమాంతర తలంపై చలిస్తూ ఉంటే అనువర్తించిన బలం చేసిన పని.
b) కంపిస్తున్న లోలకాన్ని విరామస్థితిలోకి తేవడానికి గాలి నిరోధక బలం చేసే పని.
జవాబు:
a) బలం మరియు స్థానభ్రంశం ఒకే దిశలో ఉన్నాయి, కావున పని ధనాత్మకము.
b) నిరోధక బలం చేసే పని ఋణాత్మకము.

ప్రశ్న 7.
కింద ఇచ్చిన వివరణలు సరియైనవా ? కాదా ? మీ సమాధానాలకు కారణాలు ఇవ్వండి.
a) ఏ అంతర్బలాలు, బాహ్య బలాలు పనిచేస్తున్నప్పటికి ఒక వ్యవస్థ మొత్తం శక్తి నిత్యత్వంగా ఉంటుంది.
b) చంద్రుడు భూమి చుట్టూ ఒక భ్రమణం చేయడానికి భూమి గురుత్వ బలం చేసిన పని శూన్యం.
జవాబు:
a) సరియైనది కాదు.
b) సరియైనదే. కారణం గురుత్వ బలం నిత్యత్వ బలం.

ప్రశ్న 8.
కింది సందర్భాల్లో ఏ భౌతికరాశి స్థిరంగా ఉంటుంది?
i) స్థితిస్థాపక అభిఘాతంలో
ii) అస్థితిస్థాపక అభిఘాతంలో
జవాబు:
i) స్థితిస్థాపక అభిఘాతంలో – గతిజశక్తి మరియు ద్రవ్యవేగంలు స్థిరము.
ii) అస్థితిస్థాపక అభిఘాతంలో – ద్రవ్యవేగం స్థిరం. గతిజశక్తి స్థిరం కాదు.

ప్రశ్న 9.
‘h’ ఎత్తు నుంచి స్వేచ్ఛగా కిందకు పడిన ఒక వస్తువు చదునైన నేలను తాకిన తరవాత h/2 ఎత్తుకు పైకి లేస్తే ఆ వస్తువుకు, నేలకు మధ్య ప్రత్యావస్థాన గుణకం ఎంత?
జవాబు:

ప్రశ్న 10.
స్వేచ్ఛగా కొంత ఎత్తు నుంచి భూమిపై పడ్డ వస్తువు అనేకసార్లు అదేచోట పడి లేచిన తరవాత అభిఘాతాలు ఆగిపోయే లోపు దాని మొత్తం స్థానభ్రంశం ఎంత ? వస్తువుకు, భూమికి మధ్య ప్రత్యావస్థాన గుణకం ‘e’ అనుకోండి.
జవాబు:
మొత్తం స్థానభ్రంశం S = \(\frac{h (1 + e^2)}{(1 – e^2)}\)
h = ఎత్తు, e = ప్రత్యావస్థ గుణకము.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
స్థితిజ శక్తి అంటే ఏమిటి ? గురుత్వ స్థితిజ శక్తికి సమాసాన్ని రాబట్టండి.
జవాబు:

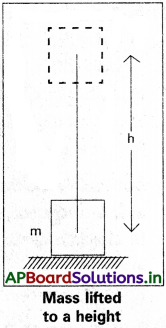
స్థితిజ శక్తి (P.E.) :
ఒక వస్తువుకు దాని స్థానం వలనగాని, స్థితి వలన గాని కలిగి శక్తిని స్థితిజ శక్తి అంటారు.
ఉదా : 1) ఎత్తున ఉన్న రిజర్వాయర్లో నిల్వ ఉన్న నీటికి గల శక్తి.
2) సాగదీసిన రబ్బరుకు గల శక్తి.

సమీకరణము :
m ద్రవ్యరాశి గల వస్తువును భూ ఉపరితలం నుండి h ఎత్తుకు తీసుకొని వెళ్ళడానికి, గురుత్వాకర్షణ బలానికి వ్యతిరేకంగా కొంత పని చేయాలి. ఈ పని ఆ వస్తువులో స్థితిజ శక్తిగా నిల్వయుండును.
గురుత్వాకర్షణ బలము F = mg
చేయవలసిన పని W = గురుత్వాకర్షణబలం × ఎత్తు
= mg × h
W = mgh
ఈ పని వస్తువులో స్థితిజ శక్తిగా నిల్వయుండును.
∴ స్థితిజశక్తి (P.E.) mgh

ప్రశ్న 2.
ఒకే ద్రవ్యవేగం కలిగి ఉన్న ఒక లారీ, కార్లను విరామస్థితికి తీసుకొని రావడానికి ఒకే బ్రేక్ బలాన్ని ఉపయోగించారు. ఏ వాహనం తక్కువ కాలంలో విరామ స్థితికి వస్తుంది? ఏ వాహనం తక్కువ దూరంలో ఆగుతుంది?
జవాబు:

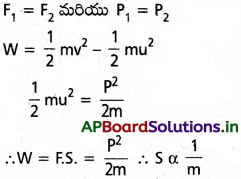
ఎక్కువ ద్రవ్యరాశి (లారీ) గల వస్తువు తక్కువ కాలంలో నిశ్చల స్థితికి వచ్చును. కావున లారీ తక్కువ దూరంలో విరామ స్థితికి వస్తుంది.

ప్రశ్న 3.
నిత్యత్వ, అనిత్యత్వ బలాల మధ్య తేడాలను రాయండి. వాటికి ఒక్కొక్క ఉదాహరణ కూడా రాయండి.
జవాబు:

ప్రశ్న 4.
ఏకమితీయ స్థితిస్థాపక అభిఘాతంలో అభిఘాతానికి ముందు రెండు వస్తువుల అభిగమన సాపేక్ష వేగం అభిఘాతం తరవాత వాటి నిగమన సాపేక్ష వేగానికి సమానం అని చూపండి.
జవాబు:

m₁, m₂ ద్రవ్యరాశులు గల నునుపుగా ఉన్న రెండు గోళాలు సరళరేఖ మార్గంలో ఒకే దిశలో ప్రయాణిస్తున్నాయి అనుకుందాము. అభిఘాతానికి పూర్వం వాటి వేగాలు u₁, u₂ (u₁ > u₂). అభిఘాతం తరువాత వాటి వేగాలు v₁, v₂. ఈ అభిఘాతం స్థితిస్థాపక అభిఘాతం.

రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమము ప్రకారము,
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ …………. (1)
m₁(u₁ – v₁) = m₂(v₂ – u₂) …………. (2)
గతిజశక్తి నిత్యత్వ నియమము ప్రకారము,

∴ అభిఘాతానికి ముందు వస్తువుల అభిగమన సాపేక్షవేగం, అభిఘాతం తరువాత వాటి నిగమన సాపేక్ష వేగానికి సమానము.

ప్రశ్న 5.
రెండు సమాన ద్రవ్యరాశులు ఏటవాలు స్థితిస్థాపక అభిఘాతం చెందినప్పుడు అభిఘాతం తరవాత అవి- ఒకదానికొకటి లంబంగా చలిస్తాయని చూపండి.
జవాబు:
ఏటవాలు స్థితిస్థాపక అభిఘాతం :
అభిఘాత వస్తువుల ద్రవ్యరాశి కేంద్రాలు, ఒక రేఖ వెంట చలించకపోతే, అటువంటి అభిఘాతాన్ని ఏటవాలు అభిఘాతం అంటారు.

రెండు సమాన ద్రవ్యరాశులు, స్థితిస్థాపక ఏటవాలు అభిఘాతం చెందిన తరువాత పరస్పరం లంబంగా చలిస్తాయి. (రెండవ వస్తువు విరామస్థితిలో ఉంటే ) :
u₂ = 0, m₁ = m₂ అయినపుడు (2) వ సమీకరణముననుసరించి, Φ = 0 అవుతుంది. (8) వ సమీకరణముననుసరించి
θ = 90°. m ద్రవ్యరాశి గల గోళం, అంతే ద్రవ్యరాశి, నిశ్చల స్థితిలో ఉన్న స్థితిస్థాపక గోళంతో ఏటవాలు అభిఘాతం చెందితే, అభిఘాతం తరువాత ఆ గోళాలు గమన దిశలు పరస్పరం లంబంగా ఉంటాయి.

ప్రశ్న 6.
కొంత ఎత్తు నుంచి స్వేచ్ఛగా కిందికి పడిన వస్తువు భూమితో ‘n’ అభిఘాతాలు చెందిన తరవాత అది పొందిన ఎత్తుకు సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
m ద్రవ్యరాశి గల చిన్న గోళం ఎత్తు నుండి స్వేచ్ఛగా పడుతూ భూమిని ‘u₁‘ వేగంతో తాకినదనుకొనుము.
అప్పుడు u₁ = √2gh ……….. (1)
గోళమును మొదటి వస్తువుగా భూమిని రెండవ వస్తువుగా తీసుకొనిన భూమి తొలి,
తుదివేగాలు వరుసగా u₂ = 0, v₂ = 0 అవుతాయి.

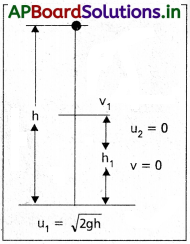
i) గోళం భూమిని తాకిన తరువాత పైకి లేచిన వేగము v₁ అనుకొనిన

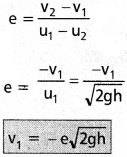
ఋణగుర్తు గోళం పైకి లేచుటను తెలియచేయును.
మొదటి అభిఘాతం తరువాత పైకి లేచిన ఎత్తు h₁ అయిన

(లేదా) h₁ = (e²)¹ h ఇక్కడ ‘ఒకటి’ అభిఘాతముల సంఖ్యను తెలియజేయును. ఇదే విధంగా 2వ అభిఘాతం తరువాత పైకి లేచిన ఎత్తు h₂ అయితే
h₂ = (e²)² h అని చూపవచ్చును.
∴ ‘n’ అభిఘాతాల తరువాత వస్తువు పైకి ఎగిరే వేగము
v_n = eⁿ √2gh
∴ పైకి పోయే ఎత్తు h_n = (e²)ⁿ h.

ప్రశ్న 7.
శక్తి నిత్యత్వ నియమాన్ని వివరించండి.
జవాబు:
ఒక వ్యవస్థ మీద పనిచేసే అంతర్బలాలు నిత్యత్వ బలాలైనపుడు, బాహ్య బలాలు పనిచేయనంత వరకు వ్యవస్థ మొత్తం యాంత్రిక శక్తి స్థిరంగా ఉండును. దీనినే శక్తి నిత్యత్వ నియమము అంటారు. కొన్ని బలాలు అనిత్యత్వ బలాలైతే, యాంత్రికశక్తిలో కొంత భాగము ఉష్ణం, కాంతి మరియు ధ్వనిగా మారును. ఒక వియుక్త వ్యవస్థలో అన్ని రూపాలలోని శక్తులను పరిగణిస్తే, మొత్తం శక్తి మారక, స్థిరంగా ఉండును. ఒక రూపంలోని శక్తిని, మరొక రూపంలోనికి మార్చవచ్చును. కాని వియుక్త వ్యవస్థ మొత్తం శక్తి స్థిరం. శక్తిని సృష్టించలేము మరియు నాశనం చేయలేము. దీనికి కారణం విశ్వం మొత్తంను, వియుక్తవ్యవస్థ దృష్టిలో చూస్తే, విశ్వం మొత్తం శక్తి స్థిరం. విశ్వంలో ఒక భాగం శక్తిని కోల్పోతే, మరియొక భాగం శక్తిని గ్రహించును.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
పని, గతిజశక్తి భావనలను అభివృద్ధిపరచి ఇది పని శక్తి సిద్ధాంతానికి దారితీస్తుందని చూపండి. [Mar. ’14]
జవాబు:
ప్రవచనం :
కణంపై నికర బలం చేసిన పని దాని గతిజశక్తిలోని మార్పుకు సమానము. i. e., k_f – k_i = W

నిరూపణ :
‘m’ ద్రవ్యరాశిగల కణము u తొలివేగం నుండి v తుదివేగం నకు చలించినట్లు భావిద్దాం. ‘a’ స్థిర త్వరణంతో S దూరం ప్రయాణించిందని భావిద్దాం. శుద్ధగతిక సంబంధం,
v² – u² = 2as …………. (1)
ఇరువైపులా \(\frac{m}{2}\) చే గుణించగా,
\(\frac{1}{2}\) mv² – \(\frac{1}{2}\)mu² = mas = FS ………….. (2)
చివరి స్టెప్ న్యూటన్స్ రెండవ నియమము నుండి తీసుకోబడింది.
(1)వ సమీకరణంను సాధారణంగా త్రిమితీయ సదిశరూపంలో క్రింది విధంగా వ్రాయవచ్చును.

నిర్ణీత స్థానభ్రంశమునకు కణంపై బలం చేసిన పని W సూచించును.
k_f – k_i = W ……………. (4)
సమీకరణం (4) పని-శక్తి సిద్ధాంతం ప్రత్యేక సందర్భము.

ప్రశ్న 2.
అభిఘాతాలు అంటే ఏమిటి? వాటిలో సాధ్యమయ్యే రకాలను వివరించండి. ఏకమితీయ స్థితిస్థాపక అభిఘాతాల సిద్ధాంతాన్ని వివరించండి.
జవాబు:
అభిఘాతం :
రెండు వస్తువుల మధ్య అన్యోన్య చర్యను అభిఘాతం అంటారు.

అభిఘాతంలు రెండు రకములు :
i) స్థితిస్థాపక అభిఘాతములు :
ద్రవ్యవేగ నిత్యత్వ మరియు గతిశక్తి నిత్యత్వ నియమాలను పాటించు అభిఘాతాలను స్థితిస్థాపక అభిఘాతాలు అంటారు.

ii) అస్థితిస్థాపక అభిఘాతములు :
ద్రవ్యవేగ నిత్యత్వ నియమం పాటించబడి, గతిజశక్తి నిత్యత్వనియమము పాటించబడని అభిఘాతాలను, అస్థితిస్థాపక అభిఘాతాలు అంటారు.

ఏకమితీయ స్థితిస్థాపక అభిఘాతము :

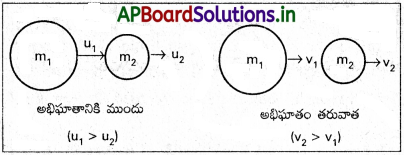
m₁, m₂ ద్రవ్యరాశులు గల నునుపుగా ఉన్న రెండు గోళాలు సరళరేఖా మార్గంలో ఒకే దిశలో ప్రయాణిస్తున్నాయి. అనుకుందాము. అభిఘాతానికి పూర్వం వాటి వేగాలు u₁, u₂ (u₁ > u₂). అభిఘాతం తరువాత వాటి వేగాలు v₁, v₂ (v₂ > v₁). ఈ అభిఘాతం స్థితిస్థాపక అభిఘాతం. స్థితిస్థాపక అభిఘాతం ద్రవ్యవేగ నిత్యత్వ మరియు గతిజశక్తి నిత్యత్వ నియమమును పాటించును.

రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమము ప్రకారము,

∴ అభిఘాతానికి ముందు వస్తువుల అభిగమన సాపేక్ష వేగం అభిఘాతం తరువాత వాటి నిగమన సాపేక్షవేగానికి సమానము.
(4)వ సమీకరణం నుండి v₂ = u₁ + v₁ – v₂
ఈ విలువను (1)వ సమీకరణంలో ప్రతిక్షేపించగా,

(5), (6) సమీకరణాలు అభిఘాతం తరువాత వస్తువుల వేగాలను తెలియచేయును.

ప్రశ్న 3.
శక్తి నిత్యత్వ నియమం తెల్పి, స్వేచ్ఛాపతన వస్తు విషయంలో శక్తినిత్యత్వ నియమంను ఋజువు చెయ్యండి. [May; Mar. ’13]
జవాబు:
శక్తి నిత్యత్వ నియమము :
నిర్వచనం :
శక్తిని సృష్టించలేము, నాశనం చేయలేము. కాని ఒక రూపం నుండి మరియొక రూపంలోనికి మార్చవచ్చు. ద్రవ్యరాశిని శక్తిగాను, శక్తిని ద్రవ్యరాశిగాను మార్చవచ్చును. విశ్వంలో అన్ని రూపాలలో ఉన్న మొత్తం శక్తి స్థిరం.

నిరూపణ :
‘m’ ద్రవ్యరాశిగల వస్తువును, ‘H’ ఎత్తుగల ప్రదేశం ‘A’ నుండి స్వేచ్ఛగా క్రిందికి జారవిడిచినామనుకొనుము.

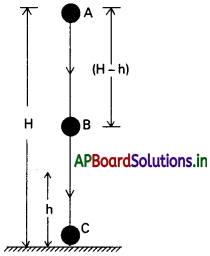
అప్పుడు మొత్తం యాంత్రికశక్తి E = K + U ఇక్కడ K = గతిజశక్తి; U = స్థితిజశక్తి. A, B, C
అనే మూడు బిందువులు వరుసగా H, h మరియు నేలపై గలవనుకొనుము.

వస్తువు A వద్ద ఉన్నప్పుడు :
వేగం = సున్నా. కావున గతిజశక్తి (K) = 0
S = H. కావున స్థితిజశక్తి (U) =mgH
A వద్ద మొత్తం యాంత్రిక శక్తి E = K + U = mgH + 0
∴ E_A = mgH ………….. (1)

వస్తువు B వద్ద ఉన్నప్పుడు :
స్వేచ్ఛగా జారవిడిచిన వస్తువు A నుండి h ఎత్తుగల బిందువు ‘B’ ని V_B వేగంతో చేరినదనుకొనుము.
B వద్ద స్థితిజశక్తి (U) = mgh

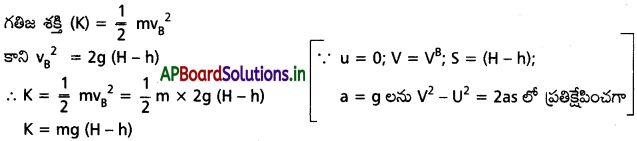
‘B’ వద్ద మొత్తం యాంత్రిక శక్తి (E_B) = K + U = mg (H – h) + mgh
= mgH – mgh + mgh
∴ E=mgH …………… (2)

వస్తువు C వద్ద (నేలపై) ఉన్నప్పుడు :
వస్తువు A నుండి బిందువు C ని V^c వేగంతో చేరిందనుకొనుము.
S = 0. కావున స్థితిజశక్తి (U) = 0

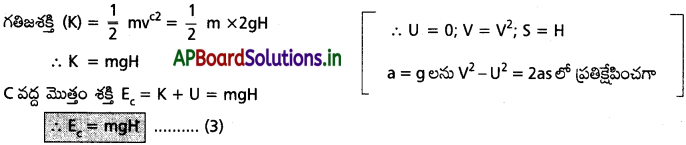
పై (1), (2), (3) సమీకరణాల నుండి వస్తువు యాంత్రిక శక్తి అన్ని బిందువుల వద్ద స్థిరము.
∴ స్వేచ్ఛగా క్రింద పడే వస్తువు విషయంలో శక్తి నిత్యత్వ నియమము ఋజువు చేయబడింది.

లెక్కలు (Problems)

ప్రశ్న 1.
10 g ద్రవ్యరాశి కలిగిన పరీక్షనాళికలో కొంత ఈథర్ ఉంది. ఈ పరీక్షనాళికను 1 g ద్రవ్యరాశి కలిగిన కార్క్ మూయడమైంది. పరీక్షనాళికను వేడిచేసినప్పుడు ఈథర్ వాయువు కలిగించే పీడనం వల్ల కార్క్ ఎగిరిపోతుంది. 5 cm పొడవు ఉన్న దృఢమైన భారరహిత కడ్డీ నుంచి ఈ పరీక్షనాళికను క్షితిజ సమాంతరంగా వేలాడదీశారు. పరీక్షనాళిక బిందువు పరంగా నిలువు వృత్తంలో తిరగాలంటే ఎంత కనీస వేగంతో కార్క్ పరీక్షనాళిక నుంచి ఎగిరిపోవాలి? (ఈథర్ ద్రవ్యరాశిని పరిగణనలోకి తీసుకో వద్దు)
సాధన:
పరీక్షనాళిక ద్రవ్యరాశి M = 10 g :
ఈథర్ ద్రవ్యరాశి m = 1g;
దృఢ కడ్డీ పొడవు = వృత్తం వ్యాసార్థం (r) = 5cm

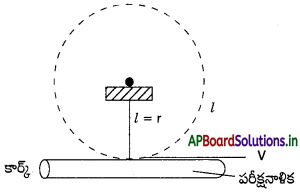
∴ r = 5 × 10^-2 m, g = 10 m s²
[∴ చర్య = – ప్రతిచర్య ]
కార్క్ వెలుపలకు వచ్చు కనీస వేగం = – v;
పరీక్ష నాళిక కనీసవేగం,

ప్రశ్న 2.
ఒక మర తుపాకి నిమిషానికి 360 బుల్లెట్లు పేల్చగలదు. వెలువడే ప్రతి బుల్లెట్ వేగం 600 ms^-1. ప్రతి బుల్లెట్ ద్రవ్యరాశి 5 gm అయితే మరతుపాకి సామర్థ్యం ఎంత? [May; Mar. ’13]
సాధన:
ఇచ్చినవి n = 360; t = 60 sec; V = ms^-1;
m = 5g = 5 × 10^-3 kg

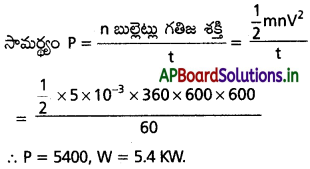
ప్రశ్న 3.
8 m లోతు ఉన్న బావి నుంచి గంటకు 3425 m³ నీటిని పైకి తోడుతున్నప్పుడు అశ్వసామర్థ్యంలో 40% వృధా అయితే ఇంజను సామర్థ్యాన్ని అశ్వ సామర్థ్యాల (horse power) లో రాబట్టండి.
సాధన:
ఇచ్చినవి V = 3425m³; d = 10³ kg m^-3; h = 8m; g = 9.8ms^-2; t = 1 గంట = 60 × 60 s

ప్రశ్న 4.
ఒక పంపు 25 m లోతు ఉన్న బావి నుంచి నిమిషానికి 600 kg ల నీటిని పైకి తోడి 50 ms^-1 వడితో బయటకు వదలాలి. దీనికి అవసరమయ్యే సామర్థ్యాన్ని లెక్కించండి.
సాధన:
ఇచ్చినవి m = 600kg; h = 25m; V = 50ms^-1
t = 60s మోటార్ సామర్థ్యం,

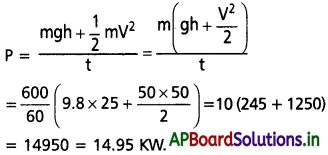
ప్రశ్న 5.
తొలుత నిశ్చల స్థితిలో ఉండి మూల బిందువు నుంచి బయలుదేరిన 5 kg ద్రవ్యరాశి ఉన్న దిమ్మెపై ధన X-అక్షం వెంట F = (20 +5x)N అనే బలం పనిచేస్తుంది. దిమ్మె x = 0 నుంచి x = 4 mకు స్థానభ్రంశం చెందినపుడు ఆ బలం చేసిన పనిని లెక్కించండి.
సాధన:
ఇచ్చినవి m =5 kg;
F = (20 + 5x)

ప్రశ్న 6.
పటంలో చూపినట్లు 5 kg ద్రవ్యరాశి ఉన్న దిమ్మె ఘర్షణ లేని వాలు తలంపై నుంచి జారుతుంది. వాలు తలం అడుగు భాగాన 600N/m బల స్థిరాంకం కలిగిన స్ప్రింగును ఏర్పాటు చేశారు. దిమ్మె వేగం గరిష్ఠమయిన క్షణంలో స్ప్రింగ్లో కలిగే సంపీడనాన్ని కనుక్కోండి.

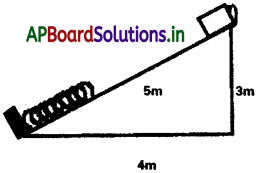
సాధన:
ఇచ్చినవి m = 5kg;
µ = 0; K = 600 N/m
4m
స్ప్రింగ్ సంకోచము ‘x’ గా తీసుకుందాము.
న్యూటన్స్ మూడవ నియమము ప్రకారము,
స్ప్రింగ్పై దిమ్మె వలన బలం F_B – స్ప్రింగ్ పునః స్థాపక బలం (F_R)
పరిమాణంలో F_B = F_R = mg sinθ = Kx
5 × 10 × \(\frac{1}{2}\) = 500 × x
⇒ x = \(\frac{30}{600}\) = 0.05m = 5cm.

ప్రశ్న 7.
x-అక్షం వెంట ఒక కణంపై F = –\(\frac{K}{x^2}\) (x ≠ 0) బలం పనిచేస్తుంది, కణం x = +a నుంచి x = +2a కి స్థానభ్రంశం చెందినప్పుడు బలం చేసిన పనిని కనుక్కోండి. Kని ధన స్థిరాంకంగా తీసుకోండి.
సాధన:

ప్రశ్న 8.
ఒక కణంపై పనిచేసే బలం F, కణ స్థానం Xతో గ్రాఫ్లో చూపించిన విధంగా మారుతుంది. x = −a నుంచి x = +2a కి కణం స్థానభ్రంశం చెందినపుడు బలం చేసిన పనిని కనుక్కోండి.

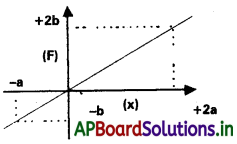
సాధన:

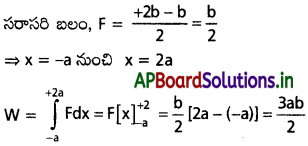
ప్రశ్న 9.
ఒక బంతిని 20m ఎత్తు నుంచి క్షితిజ సమాంతర నేల మీదకు 20 m/s తొలి వేగంతో కిందికి విసిరారు. నేలను తాకిన తరువాత బంతి అంతే ఎత్తుకు పైకి లేచింది. ఈ అభిఘాతంలో బంతికి, నేలకు మధ్య ప్రత్యావస్థాన గుణకం కనుక్కోండి.

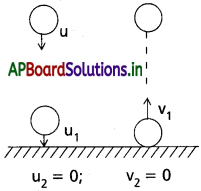
సాధన:
ఇచ్చినవి u = 20 m/s; h = 20m; g = 10m/s²
v = u₁ (అనుకుందాం)

భూమి నిశ్చల స్థితిలో ఉండును. కావున
u₂ = 0; v₂ = 0

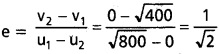
ప్రశ్న 10.
స్వేచ్ఛగా 10 m ఎత్తు నుంచి ద్రుఢమైన క్షితిజ సమాంతర తలంపై పడిన బంతి అనేకసార్లు అదేచోట పడిలేచిన తరువాత నిశ్చల స్థితికి వచ్చేలోగా బంతి ప్రయాణించిన మొత్తం దూరం ఎంత? బంతికి, తలానికి మధ్య ప్రత్యావస్థాన గుణకం \(\frac{1}{\sqrt{2}}\) అనుకోండి.
సాధన:

అదనపు లెక్కలు (Additional Problems)

ప్రశ్న 1.
వస్తువుపై బలం చేసిన పని సంజ్ఞ గురించి అర్థం చేసుకోవడం చాలా ముఖ్యమైంది. కింది భౌతికరాశులు, ధనాత్మకమా? రుణాత్మకమా? జాగ్రత్తగా తెలియచేయండి.
a) బకెట్ను బిగించిన తాడు సహాయంతో బావి నుండి బకెట్ను తీసే సందర్భంలో మనిషి చేసిన పని.
b) పై సందర్భానికి గురుత్వ బలం చేసిన పని.
c) ఒక వస్తువు వాలు తలంపై జారుతున్నప్పుడు ఘర్షణ బలం చేసిన పని.
d) ఘర్షణ ఉన్న (గరుకు) క్షితిజ సమాంతర తలంపై వస్తువు సమ వేగంతో చలిస్తున్నప్పుడు అనువర్తించిన బలం చేసిన పని.
e) కంపిస్తున్న లోలకాన్ని విరామస్థితిలోకి తేవడానికి గాలి నిరోధక బలం చేసే పని.
సాధన:
జరిగిన పని W = \(\overrightarrow{F}.\overrightarrow{S}\) = FS cosθ ఇచ్చట θ, బలం \(\overline{\mathrm{F}}\) మరియు స్థానభ్రంశం \(\overrightarrow{S}\) ల మధ్య స్వల్పకోణం.

a) బకెట్ను పైకి లేపుటకు, బకెట్ బరువుకు సమానమైన బలంను నిలువుగా పైకి ప్రయోగించాలి. i.e., θ = 0°, W = FS cos 0° = FS. ఇది ధనాత్మకము.

b) గురుత్వాకర్షణ బలంనకు వ్యతిరేకంగా బకెట్ చలించుట వల్ల θ = 180°.
W = FS cos 180° = -FS: ఇది ఋణాత్మకం.

c) మర్షణ బలం ఎల్లప్పుడు సాపేక్ష చలనంను వ్యతిరేకించును.

d) ప్రయోగించిన బలదిశలో, వస్తువు చలిస్తే θ = 0° W = FS cos 0° = FS. ఇది ధనాత్మకము.

e) గోళం చలనంనకు వ్యతిరేకంగా నిరోధ బలం దిశ ఉండును. i.e. θ = 180°. ఈ సందర్భంలో జరిగిన పని ఋణాత్మకము.

ప్రశ్న 2.
గతిక ఘర్షణ గుణకం 0.1. కలిగిన బల్లపై నిశ్చల స్థితిలో 2kg ద్రవ్యరాశి ఉన్న వస్తువు 7 N క్షితిజ సమాంతర బలం వల్ల చలిస్తూ ఉంది. కింది రాశులను లెక్కించండి.
a) 10s కాలంలో అనువర్తిత బలం చేసిన పని.
b) 10s కాలంలో ఘర్షణ బలం చేసిన పని.
c) 10s కాలంలో నికర బలం చేసిన పని.
d). 10s కాలంలో వస్తువు గతిజ శక్తిలోని మార్పు.
మీ ఫలితాలను వివరించండి.
సాధన:
m = 2kg, u = 0, F = 7N; µ = 0.1, ఇచ్చినది
W = 2, t 10s
బలప్రయోగం ఏర్పడు త్వరణం;
a = – \(\frac{F}{m}=\frac{7}{2}\) = = m 2 = 3.5 m/s²
ఘర్షణ బలం, f = µR
= µmg = 0.1 × 2 × 9:8 1.96 N
ఘర్షణ వల్ల ఏర్పడు అపత్వరణము
a₂ = –\(\frac{F}{m}=\frac{-1.96}{2}\) = 0.98 m/s²
వస్తువు చలిస్తున్నప్పుడు నికర త్వరణం = a₁ + a₂
= 3.5 – 0.98 = 2.52m/s²
10 sec. లో వస్తువు ప్రయాణించిన దూరం
S = Ut + \(\frac{1}{2}\)at²
= 0 + \(\frac{1}{2}\) × 2.52 × (10)² = 126m.

a) ప్రయోగించిన బలం చేయు పని = F × S
W₁ = 7 × 126 = 882J

b) ఘర్షణ బలం చేయు పని W₂ -f × s
-1.96 × 126 = 246.9J

c) నికర బలం చేయు పని
W₃ = నికర బలం × దూరం
= (F – f)s = (7 – 1.96)126 = 635 J.
\(\frac{1}{2}\)

d) v = u + at నుండి
v = 0 + 2.52 × 10 = 25.2 m^s-1
తుది K.E = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) × 2 × (25.2)²
= 635J
తొలి K.E = \(\frac{1}{2}\) mu² = 0
∴ K.Eలో మార్పు = 635 – 0 = 635 J.
∴ వస్తువు K.E లో మార్పు, దానిపై జరిగిన నికర బలంనకు సమానమని సూచిస్తుంది.

ప్రశ్న 3.
పటంలో కొన్ని ఏకమితీయ స్థితిజ శక్తి ప్రయేయాలకు ఉదాహరణలు ఇవ్వడమైంది. కణం మొత్తం శక్తిని ద్వితీయ నిరూపక అక్షం (y-అక్షం) పై క్రాస్ (cross) తో సూచించడమైంది. ఇచ్చిన శక్తికి, కణాన్ని కనుక్కోలేని ప్రాంతం ఏదైనా ఉంటే ఆ ప్రాంతాన్ని ప్రతి సందర్భానికి వివరించండి. ప్రతి సందర్భంలో కణానికి ఉండవలసిన మొత్తం కనీస శక్తిని కూడా సూచించండి. ఈ స్థితిజ శక్తి ఆకారాలకు సంబంధించిన సరళమైన భౌతిక సందర్భాలను ఆలోచించండి.


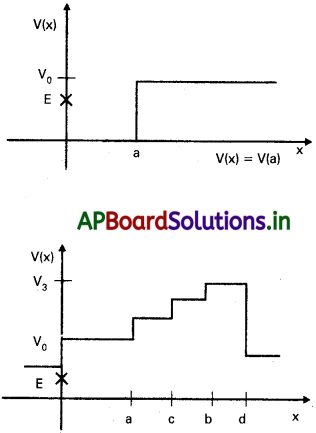
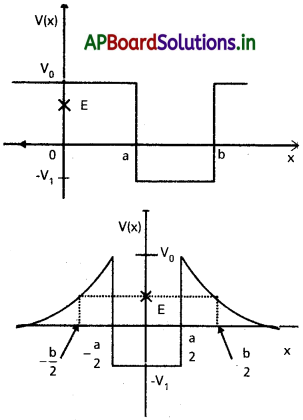
సాధన:
మొత్తం శక్తి E = K.E + P.E (లేక) K.E = E – P.E
మరియు K.E ఎప్పుడు ఋణాత్మకం కాదు. K.E ఋణాత్మకమైతే, ఆ ప్రాంతంలో వస్తువు

i) x >a, P.E (v₀) > E
∴ K.E ఋణాత్మకం కావున వస్తువు × > a ప్రాంతంలో ఉండదు.

ii) x < a మరియు x > b, P.E (v_o) > E
∴ K.E ఋణాత్మకం. కావున వస్తువు x < a మరియు x > b ప్రాంతంలో ఉండదు.

iii) ప్రతి ప్రాంతంలో P.E (v₀) > E. కావున వస్తువు ఆ ప్రాంతంలో ఉండదు.

iv) -b/2 < x < a/2 మరియు a/2 < x < b/2 ప్రాంతంలో వస్తువు ఉండదు.

ప్రశ్న 4.
రేఖీయ సరళహరాత్మక చలనం చేస్తున్న కణం స్థితిజ శక్తి ప్రమేయం V(x) = kx²/2 గా ఇవ్వడమైంది. ఇక్కడ k డోలకం బల స్థిరాంకం k= 0.5 N m^-1 విలువకు V(x), x ల మధ్య గ్రాఫ్ పటంతో చూపించడమైంది. ఈ పొటెన్షియల్లో చలించే 1 J మొత్తం శక్తి కలిగిన కణం x = ± 2m కే చేరినపుడు అది వెనకకు మరలుతుందని చూపండి.

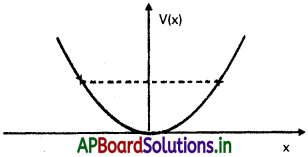
సాధన:
ఏదైనా క్షణాన, డోలకం మొత్తం శక్తి K.E మరియు P.Eల
మొత్తంనకు సమానము.
i.e; E = K.E + P.E
E = K.E + P.E, E = \(\frac{1}{2}\)mu² + \(\frac{1}{2}\)kx²
కణం వేగం సున్నా అయిన తరువాత, వెనుకకు వచ్చును.
i.e. u = 0.
∴ E = 0 + \(\frac{1}{2}\)kx², E = 1 జౌల్ మరియు
K = \(\frac{1}{2}\)N/m
∴ 1 = \(\frac{1}{2}\) × \(\frac{1}{2}\)x² (లేక) x² = 4, x = ± 2m.

ప్రశ్న 5.
కింది వాటికి సమాధానాలివ్వండి.
a) రాకెట్ గమనంలో ఉన్నపుడు దాని చుట్టూ ఉన్న కప్పు (casing) మర్షణ వల్ల కాలిపోతుంది. కాలిపోవడానికి అవసరమయ్యే ఉష్ణ శక్తి రాకెట్ నుంచి లభ్యమవుతుందా? లేదా వాతావరణం నుంచి లభ్యమవుతుందా?

b) అధిక దీర్ఘాక్ష దీర్ఘవృత్తాకార కక్ష్యల్లో తోకచుక్కలు సూర్యుని చుట్టూ తిరుగుతూ ఉంటాయి. సూర్యుని వల్ల తోకచుక్కపై పనిచేసే గురుత్వ బలం సాధారణంగా తోకచుక్క వేగానికి లంబంగా ఉండదు. కాని తోకచుక్క ప్రతి పూర్తి భ్రమణానికి గురుత్వ బలం చేసిన పని శూన్యమవుతుంది. ఎందుకు?

c) పలుచని వాతావరణంలో భూమి చుట్టూ తిరుగుతున్న కృత్రిమ ఉపగ్రహం వాతావరణ నిరోధం వల్ల క్రమంగా చాలా స్వల్ప మోతాదులో శక్తిని కోల్పోతుంది. అయితే అది భూమిని దగ్గరగా సమీపిస్తున్న కొద్దీ దాని వడి ఎందుకు క్రమంగా పెరుగుతుంది?

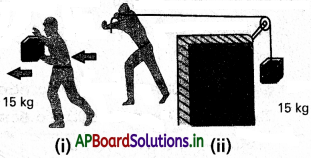
d) పటం (i) లో ఒక మనిషి 15 kg ద్రవ్యరాశిని తన చేతులతో తీసుకొని వెళ్తూ 2 m దూరం నడిచాడు. పటం (ii), లో అతను తన వెనక ఉన్న తాడును లాగుతూ అంతే దూరాన్ని నడిచాడు. కప్పీ మీదగా వెళ్తున్న తాడుకు రెండవ చివర 15 kg ద్రవ్యరాశి వేలాడదీయడమైంది. ఏ సందర్భంలో జరిగిన పని ఎక్కువ?
సాధన:
a) రాకెట్ మొత్తం శక్తి ఎగురుతున్నప్పుడు దాని ద్రవ్యరాశిపై ఆధారపడును. i.e. P.E + K.E = mgh + \(\frac{1}{2}\)mv². రాకెట్ చుట్టు ఉన్న పేటిక దహనమయితే, దాని ద్రవ్యరాశి తగ్గుతుంది. రాకెటె మొత్తం శక్తి తగ్గును. దహనానికి కావాల్సిన ఉష్ణశక్తిని, వాతావరణం నుంచి కాక రాకెట్, తననుంచే సమకూర్చును.

b) దీనికి కారణం గురుత్వాకర్షణ బలం నిత్యత్వ బలం. సూర్యుని కక్ష్యలో తోకచుక్క ఒక పూర్తి భ్రమణం చేయటంలో గురుత్వాకర్షణ బలం చేయు పని సున్నా.

c) భూమి కక్ష్యలో కృత్రిమ ఉపగ్రహం, భూమికి దగ్గరగా సమీపిస్తున్నప్పుడు, స్థితిజశక్తి తగ్గును. స్థితిజశక్తి మరియు గతిజశక్తి స్థిరం. కావున ఉపగ్రహం K.E పెరుగు తున్నప్పుడు, వేగం కూడా పెరుగును. వాతావరణ నిరోధం ఉపగ్రహం మొత్తం శక్తిని స్వల్పంగా తగ్గిస్తుంది.

d) పటం (i)లో వ్యక్తి ద్రవ్యరాశిపై ప్రయోగించిన బలం నిలువు ఊర్ధ్వ దిశలో క్షితిజ సమాంతరంగా వస్తువు కొంతదూరం చలించును.
∴ θ = 90°, W = FS cos 90° = zero.
పటం (ii)లో, బలంను క్షితిజ సమాంతరంగా ప్రయోగిస్తే, క్షితిజ సమాంతరంగా వస్తువు
కొంతదూరం చలించును. θ = 0°.
W = FS cosυ = mg × S cos0°
W = 15 × 9.8 × 2 × 1 = 294 Joule.
∴ 2వ సందర్భంలో జరిగిన పని ఎక్కువ.

ప్రశ్న 6.
సరైన ప్రత్యామ్నాయం కింద గీత గీయండి.
a) వస్తువుపై నిత్యత్వ బలం చేసిన పని ధనాత్మకమయితే, వస్తువు స్థితిజ శక్తి పెరుగుతుంది/తగ్గుతుంది/మారకుండా ఉంటుంది.
b) ఘర్షణకు వ్యతిరేకంగా వస్తువు పనిచేయడం వల్ల ఎప్పుడు గతిజ/స్థితిజ శక్తి నష్టం జరుగుతుంది.
c) అనేక కణ వ్యవస్థ యొక్క ద్రవ్యవేగంలోని మార్పురేటు బాహ్యబలం/వ్యవస్థలోని అంతర బలాల మొత్తానికి అనులోమానుపాతంలో ఉంటుంది.
d) రెండు వస్తువుల మధ్య జరిగిన అస్థితి స్థాపక అభిఘాతంలో, అభిఘాతం తరవాత వ్యవస్థ మొత్తం గతిజ శక్తి / మొత్తం రేఖీయ ద్రవ్యవేగం / మొత్తం శక్తి మారకుండా స్థిరంగా ఉంటుంది.
సాధన:
a) వస్తువు స్థితిజశక్తి తగ్గును. వస్తువు బలదిశలో స్థానభ్రంశం చెందితే, వస్తువుపై నిత్యత్వ బలం చేయు పని ధనాత్మకం. వస్తువు కేంద్రక బలంను సమీపిస్తున్నప్పుడు, తగ్గుదల x కావున P.E తగ్గును.

b) ఘర్షణకు వ్యతిరేకంగా వస్తువు చేయుపని,దాని గతిజశక్తిని సమకూరుస్తుంది. కావున K.E తగ్గును.

c) వ్యవస్థ మొత్తం లేక నికర ద్రవ్యవేగంను, అంతరిక వు. బహుళకణ వ్యవస్థ మొత్తం ద్రవ్య బలాలు మార్చవు. వేగంలోని మార్పురేటు, వ్యవస్థపై బాహ్య బలంనకు అనులోమానుపాతంలో ఉంటుంది.

d) రెండు వస్తువులు అస్థితిస్థాపక అభిఘాతంలో, అభిఘాతం తరువాత మొత్తం రేఖీయ ద్రవ్యవేగం మరియు మొత్తం శక్తిలో మార్పు ఉండదు. మొత్తం శక్తిలో కొంతశక్తి ఇతర రూపాలలోనికి మారును.

ప్రశ్న 7.
కింద ఇచ్చిన ప్రతిపాదనలు సరిఅయినవా? కావా? మీ సమాధానాలకు కారణాలు రాయండి.
a) రెండు వస్తువుల మధ్య జరిగే స్థితిస్థాపక అభిమాతంలో ప్రతి వస్తువు యొక్క ద్రవ్యవేగం, శక్తి నిత్యత్వంగా ఉంటుంది.
b) వస్తువుపై ఎటువంటి అంతర, బాహ్యబలాలు పనిచేసినప్పటికి వ్యవస్థ మొత్తం శక్తి ఎప్పుడూ నిత్యత్వంగా ఉంటుంది.
c)ఒక సంవృత ఉచ్చు (loop) వెంబడి చలనంలో ఉన్న వస్తువుపై ప్రకృతిలోని ప్రతిబలం చేసే పని శూన్యం.
d) అస్థితిస్థాపక అభిఘాతంలో వ్యవస్థ తొలి గతిజ శక్తి కంటె తుది గతిజ శక్తి ఎప్పుడూ తక్కువగా ఉంటుంది.
సాధన:
a) వ్యవస్థ మొత్తం ద్రవ్యవేగం మరియు మొత్తం శక్తి నిత్యత్వం అగును. ప్రతి వస్తువుకు కాదు. కావున ఇచ్చిన స్టేట్మెంట్ తప్పు.

b) వస్తువుపై బాహ్యబలం, వస్తువుపై మొత్తం శక్తి మారును. కావున ఇచ్చిన స్టేట్మెంట్ తప్పు.

c) వస్తువు, నిత్యత్వ బలాలకు గురుత్వాకర్షణ మరియు స్థిర విద్యుదాకర్షణ బలంలకు లోనై సంవృత పథంలో చలిస్తున్నప్పుడు చేయుపని సున్నా. అనిత్యత్వ బలాలు చేయుపని సున్నా కాదు. ఉదా : ఘర్షణ బలాలు.

d) అస్థితి స్థాపక అభిఘాతంలో, కాంతి గతిజశక్తి మరొక రూపంలోనికి మారును. కావున ఇచ్చిన స్టేట్మెంట్
నిజము.

ప్రశ్న 8.
తగిన కారణాలతో జాగ్రత్తగా సమాధానమివ్వండి :
a) రెండు బిలియర్డ్ బంతుల స్థితిస్థాపక అభిఘాతంలో బంతుల మధ్య అభిఘాతం జరుగుతున్న స్వల్ప కాలంలో (ఒక దానితో ఒకటి స్పర్శించుకొన్నప్పుడు) మొత్తం గతిజ శక్తి నిత్యత్వంగా ఉంటుందా?
b) స్వల్ప కాలవ్యవధిలో రెండు బంతుల మధ్య జరిగిన స్థితిస్థాపక అభిఘాతంలో రేఖీయ ద్రవ్యవేగం మొత్తం నిత్యత్వంగా ఉంటుందా?
c) అస్థితిస్థాపక అభిఘాతానికి (a), (b) లకు సమాధానాలు ఏమిటి?
d) రెండు బిలియర్డ్ బంతుల స్థితిజ శక్తి, వాటి కేంద్రాల మధ్య దూరంపై మాత్రమే ఆధారపడితే ఆ అభిఘాతం స్థితిస్థాపకమా లేదా అస్థితిస్థాపకమా?
(సూచన : అభిఘాత సమయమప్పుడు ఉండే బలానికి సంబంధించిన స్థితిజ శక్తి గురించి మాట్లాడుతున్నాం కాని గురుత్వ స్థితిజ శక్తిని -గురించి కాదు.)
సాధన:
a) కాదు. స్థితిస్థాపక అభిఘాతంలో K.E నిత్యత్వం కాదు. స్థితిస్థాపక అభిఘాతానికి ముందు తరువాత K.E. సమానం. స్థితిస్థాపక అభిఘాతంలో బంతి K.E స్థితిజ శక్తిగా మారును.

b) అవును. రెండు బంతులు స్వల్పకాల స్థితిస్థాపక అభిఘాతంలో మొత్తం రేఖీయ ద్రవ్యవేగం నిత్యత్వం అగును.

c) అస్థితిస్థాపక అభిఘాతంలో, అభిఘాతం తరువాత, “ మొత్తం K.E నిత్యత్వం కాదు. అభిఘాతం తరువాత, మొత్తం ద్రవ్యవేగం నిత్యత్వమగును.

d) అభిఘాతం స్థితిస్థాపకం అయితే, బలాలు నిత్యత్వం అగును.

ప్రశ్న 9.
నిశ్చల స్థితి నుండి బయలుదేరిన ఒక వస్తువు స్థిర త్వరణంతో ఏకమితీయ చలనం కలిగి ఉంది. t కాలంలో దానికి అందచేసిన సామర్థ్యం కింది వాటికి అనులోమానుపాతంలో ఉంటుంది.
i) t^1/2
ii) t
iii) t^3/2
iv) t²
సాధన:
v = u + at, v = 0 + at = at నుండి
సామర్థ్యం, ρ= F × v = (ma) × at = ma²t
m మరియు a లు స్థిరాంకాలు, ∴ p α t.

ప్రశ్న 10.
స్థిర సామర్థ్యాన్ని అందించే జనకం ప్రభావం వల్ల ఒక వస్తువు ఏక దిశాత్మకంగా చలిస్తుంది. t కాలంలో కలిగిన స్థానభ్రంశం కింది వాటికి అనులోమానుపాతంలో ఉంటుంది.
i) t^1/2
ii) t
iii) t^3/2
iv) t²
సాధన:
సామర్థ్యం, P = బలం × వేగం
∴ P = [MLT^-2] [LT^-1] = [mL²T^-3]
P = [mL²T^-3] = స్థిరం
∴ L² T^-3 = స్థిరం
∴ L² α T³ (లేక) L a T^3/2
(లేదా) \(\frac{L^2}{T^3}\) = స్థిరం

ప్రశ్న 11.
ఒక నిరూపక వ్యవస్థలో అక్షం వెంట చలనానికి పరిమితం అయిన వస్తువుపై
F = –\(\hat{\mathbf{i}}\) + 2\(\hat{\mathbf{j}}\) + 3\(\hat{\mathbf{k}}\) N
అనే స్థిర బలం పనిచేస్తుంది. ఇక్కడ x−, y−, z–అక్షాల వెంట ప్రమాణ సదిశలు వరుసగా \(\hat{\mathbf{i}},\hat{\mathbf{j}},\hat{\mathbf{k}}\) z–అక్షంపై 4 m దూరం చలించడానికి ఈ బలం చేసిన పని ఎంత?
సాధన:

ప్రశ్న 12.
విశ్వ కిరణాల ప్రయోగంలో 10 keV, 100 keV. శక్తిగల ఎలక్ట్రాన్, ప్రోటాన్లను కనుగొన్నారు. వీటిలో వేగవంతం అయినది ఏది? ఎలక్ట్రాన్ లేదా ప్రోటాన్? వాటి వడుల నిష్పత్తిని రాబట్టండి. (ఎలక్ట్రాన్ ద్రవ్యరాశి = 9.11 × 10^-31 kg, ప్రోటాన్ ద్రవ్యరాశి = 1.67 × 10^-27kg , 1 eV = 1.60 × 10^-19 J).
సాధన:

ప్రశ్న 13.
500 m ఎత్తు నుంచి 2 mm వ్యాసార్థం ఉన్న వాన నీటి బిందువు నేలపై పడుతుంది. సగం ఎత్తువరకు తగ్గుతున్న త్వరణం (గాలి స్నిగ్ధతా నిరోధం వల్ల) కలిగి గరిష్ట (అంత్య) వడిని పొందుతుంది. ఆ తరువాత అది ఏకరీతివడితో కిందికి చలిస్తుంది. వాన నీటి బిందువు ప్రయాణంలో, మొదటి, రెండవ సగంలో గురుత్వ బలం చేసిన పని ఎంత? 10 m s^-1 వడితో నేలను చేరినట్లైతే దాని పూర్తి ప్రయాణంలో నిరోధక బలం చేసిన పని ఎంత?
సాధన:
r = 2mm = 2 × 10^-3m
ప్రతి అర్థప్రయాణంలో, చలించు దూరం
S = \(\frac{500}{2}\) = 250 m
నీటి సాంద్రత ρ = 10³ kg/m³
వర్షం బిందువు ద్రవ్యరాశి = బిందువు ఘనపరిమాణం × సాంద్రత
m = \(\frac{4}{3}\)πr³ × ρ = \(\frac{4}{3}\times\frac{22}{7}\)(2 × 10^-3)³ × 10³ = 3.35 × 10^-5 kg
w = mg × s = 3.35 × 10^-5 × 9.8 × 250 =0.082J

వర్షం బిందువు త్వరణం తగ్గుతూ లేక ఏకరీతి వడితో చలిస్తూ ఉన్నప్పుడు, వర్షం బిందువుపై గురుత్వాకర్షణ బలం చేయు పని స్థిరం.

నిరోధక బలాలు లేనప్పుడు, భూమిని చేరు బిందువు శక్తి.
E₁ = mgh = 3.35 × 10^-5 × 9.8 × 500
= 0.164J

వాస్తవ శక్తి E₂ = \(\frac{1}{2}\)mv²
\(\frac{1}{2}\) × 3.35 × 10^-5 × (10)²
= 1.675 × 10^-3 J.
∴ నిరోధక బలాలు చేయు పని
W = E₁ – E₂ = 0.164 – 1.675 × (10)^-3
W = 0.1623 ఔల్స్

ప్రశ్న 14.
పాత్రలో ఉన్న వాయువులోని అణువు 200m s^-1 వడితో, లంబంతో 30° కోణం చేస్తున్న దిశలో క్షితిజ సమాంతర(పాత్ర) గోడను ఢీకొని అంతే వడితో వెనకకు మరలింది. ఈ అభిఘాతంలో ద్రవ్యవేగం నిత్యత్వంగా ఉంటుందా? ఈ అభిఘాతం స్థితిస్థాపకమా లేదా అస్థితిస్థాపకమా?
సాధన:
స్థితిస్థాపక మరియు అస్థితిస్థాపక అభిఘాతంలో ద్రవ్యవేగం నిత్యత్వమగును. K. E నిత్యత్వం అవుతుందో, లేదో చెక్ చేద్దాం.

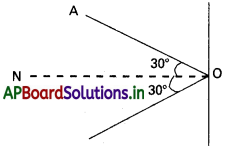
పటంలో చూపినట్లు గోడ ఎక్కువ మందంగా ఉన్నప్పుడు, ప్రత్యావర్తన అణువు గోడ పై వేగంను కలుగచేయదు.

m వాయు అణువు ద్రవ్యరాశి మరియు M గోడ ద్రవ్యరాశి అయితే, అభిఘాతం తరువాత మొత్తం ‘ K.E
E₂ = \(\frac{1}{2}\) m(200)² + \(\frac{1}{2}\)m(0)²
E₂ = 2 × 10⁴ mj
అభిఘాతంనకు ముందు అణువు K.E.
[E₁ = \(\frac{1}{2}\)m(200)² = 2 × 10⁴ mJ mu].
కావున అభిఘాతం స్థితిస్థాపక అభిఘాతం.

ప్రశ్న 15.
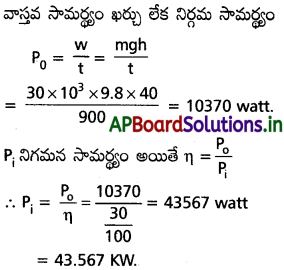
భవనం నేల అంతస్తు (ground floor) పై ఉన్న పంప్ (మోటార్) 30m3 ఘనపరిమాణం ఉన్న టాంకును 15 నిమిషాలలో నింపగలదు. పంప్ దక్షత 30% కలిగి ఉండి, టాంక్ నేలపై నుంచి 40 m ఎత్తులో ఉంటే పంప్ ఎంత విద్యుత్ సామర్థ్యం వినియోగించుకొంటుంది ?
సాధన:
నీటి ఘనపరిమాణం = 30 m³,
t = 15 min = 15 × 60 = 900s.
ఎత్తు h = 40m, దక్షత η = 30%
నీటిసాంద్రత = p = 10³ kg/m³
∴ నీటి పంపింగ్ ద్రవ్యరాశి m = ఘనపరిమాణం × సాంద్రత = 30 × 10³ kg·

ప్రశ్న 16.
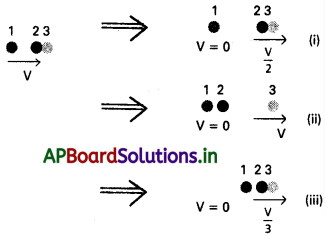
ఘర్షణ లేని బల్లపై రెండు సర్వసమాన బాలే బేరింగ్లు ఒక దానితో ఒకటి స్పర్శించుకొంటూ నిశ్చలంగా ఉన్నాయి. అంతే ద్రవ్యరాశి ఉన్న వేరొక బాల్బేరింగు. V తొలి వడితో వీటిని సూటిగా ఢీకొంది. ఇది స్థితిస్థాపక అభిఘాతమయితే, అభిఘాతం తరవాత పక్క వాటిలో (పటం) ఏది సాధ్యమయ్యే ఫలితమవుతుంది?

సాధన:
ప్రతి బాల్బేరింగ్ ద్రవ్యరాశి mగా తీసుకుందాము. అభిఘాతం ముందు, వ్యవస్థ మొత్తం K.E
= \(\frac{1}{2}\)mV² + 0 = \(\frac{1}{2}\)mV²
అభిఘాతం తరువాత, వ్యవస్థ మొత్తం K.E
సందర్భం I, E₁ = \(\frac{1}{2}\) (2m) (V/2)² = \(\frac{1}{4}\)mV²
సందర్భం II, E₂ = \(\frac{1}{2}\)mV²
సందర్భం III, E₃ = \(\frac{1}{2}\)(3m) (V/3)² = \(\frac{1}{6}\)mV²

సందర్భం II లో మాత్రమే K.E నిత్యత్వమగును. కావున సందర్భం II మాత్రమే సాధ్యం.

ప్రశ్న 17.
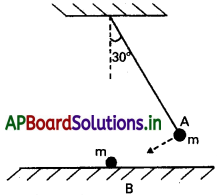
క్షితిజ లంబానికి 30° కోణం చేస్తూ ఉన్న లోలక గోళం A ని వదిలితే అది బల్లపై నిశ్చలస్థితిలో ఉన్న అంతే ద్రవ్యరాశి కలిగిన B గోళాన్ని పటం లో చూపినట్లు ఢీకొంది. అభిఘాతం తరవాత A గోళం ఎంత ఎత్తుకు లేస్తుంది ? అభిఘాతం స్థితిస్థాపకం అని ఊహించి, గోళాల పరిమాణాలను ఉపేక్షించండి.

సాధన:
గోళం A పైకి లేవదు. దీనివల్ల ఒకే ద్రవ్యరాశి గల రెండు వస్తువులు స్థితిస్థాపక అభిఘాతంలో వాని వేగాలు మార్చుకొనును. అభిఘాతం తరువాత బంతి A విరామ స్థితికి మరియు బంతి B, A బంతి వేగంతో చలించును.

ప్రశ్న 18.
ఒక లోలక గోళాన్ని క్షితిజ సమాంతర స్థానం నుంచి విడిచిపెట్టారు. గాలి నిరోధం వల్ల తొలి శక్తిలో 5% దుర్వ్యయమయితే గోళం అత్యంత నిమ్నతమ బిందువును ఎంత వడితో చేరుతుంది? లోలకం పొడవు 1.5 m.
సాధన:
h = 1.5m, V =?
దుర్యయమగు శక్తి = 5%
గోళం కనిష్ట స్థానం B అయితే, B వద్ద దాని స్థితిజ శక్తి సున్నా, క్షితిజ సమాంతర స్థానం A వద్ద, గోళం మొత్తం స్థితిజశక్తి mgh.
A నుండి Bకు చలించుటలో, గోళం P.E, K.Eగా మారును. మారిన శక్తి = 95% (mgh)
B వద్ద వేగం V అయితే, అప్పుడు K.E = \(\frac{1}{2}\)mv²
= \(\frac{95}{100}\) mgh

ప్రశ్న 19.
25 kg ద్రవ్యరాశి ఉన్న ఇసుక సంచిని మోస్తున్న 300 kg ద్రవ్యరాశి కలిగిన ట్రాలీ ఘర్షణ లేని బాట (track) లో 27 km/h ఏకరీతి వడితో చలిస్తూ ఉంది. కొంతసేపటి తరవాత సంచికి కలిగిన రంధ్రం ద్వారా 0.05 kg s 1 రేటుతో ఇసుక ట్రాలీ తలంపై లీకు (leak) అవుతూ ఉంది. ఇసుక సంచి ఖాళీ అయిన తరవాత ట్రాలీ వడి ఎంత?
సాధన:
ట్రాలీ ఇసుక బస్తాతో ఏకరీతిగా చలిస్తుంటే, వ్యవస్థపై బాహ్యబలం = సున్నా.
ఇసుక బస్తా నుండి లీక్ అయితే, ట్రాలీపై బాహ్యబలం పని చేయదు. కావున ట్రాలీ వడి మారదు.

ప్రశ్న 20.
0.5 kg ద్రవ్యరాశి ఉన్న వస్తువు సరళరేఖా మార్గంలో v = ax^3/2 వేగంతో ప్రయాణిస్తుంది. ఇక్కడ a = 5m^-1/2 s^-1. అది x = 0 నుంచి x = 2 m స్థానభ్రంశం చెందినపుడు ఫలిత బలం చేసిన పని ఎంత?
సాధన:
m = 0.5 kg; v = ax^3/2, a = 5m^-1/2 s^-1,
w = ?
x = వద్ద తొలివేగం, v₁ = a × 0 = 0
x = 2 వద్ద తుదివేగం, v₂ = a2^3/2 = 5 × 2^3/2
జరిగిన పని = K.E లో పెరుగుదల = \(\frac{1}{2}\)m
(v₂² – v₁²), W = \(\frac{1}{2}\) × 0.5 [(5 × 2^3/2)²) – 0] = 50J

ప్రశ్న 21.
ఒక గాలిమర (windmill) రెక్కలు A వైశాల్యం ఉన్న వృత్తాన్ని చిమ్ముతున్నాయి. (a) ఈ వృత్తానికి లంబంగా v వేగంతో గాలి ప్రవహిస్తుంటే, దీని ద్వారా t కాలంలో వెళ్ళే గాలి ద్రవ్యరాశి ఎంత? (b) గాలి గతిజ శక్తి ఎంత? (c) గాలి మర, గాలి శక్తిలో 25% శక్తిని విద్యుత్ శక్తిగా మారుస్తుందని 30 m², v = 36 km/h గాలి సాంద్రత 1.2 kg m^-3 ఉత్పత్తి అయ్యే విద్యుత్ సామర్థ్యం ఎంత?
సాధన:
a) గాలి ప్రవాహ ఘనపరిమాణం/సెకండుకు = AV
గాలి ప్రవాహ ద్రవ్యరాశి / సెకండుకు = AVρ
t secలో ప్రవహించు గాలిద్రవ్యరాశి = AVρt

ప్రశ్న 22.
బరువు తగ్గాలనుకొనే వ్యక్తి (dieter) 10kg ద్రవ్యరాశిని ప్రతిసారి 0.5 m ఎత్తుకు లేపుతూ వెయ్యిసార్లు పైకి ఎత్తాడు. అతడు ప్రతిసారి ద్రవ్యరాశిని కిందకు దించేటప్పుడు నష్టపోయిన స్థితిజ శక్తి దుర్వ్యయమవుతుందని ఊహించండి. (a) గురుత్వ బలానికి వ్యతిరేకంగా అతడు చేసిన పని ఎంత? (b) ప్రతి కిలో గ్రాముకు 3.8 × 107J శక్తిని కొవ్వు అందిస్తుంది. ఇది 20% దక్షతతో యాంత్రిక శక్తిగా మారుతుంది. బరువు తగ్గాలనుకొనే వ్యక్తి ఎంత కొవ్వును ఉపయోగించినట్లు?
సాధన:
m = 10kg, b = 0.5 m, n = 1000
a) గురుత్వాకర్షణ బలంనకు వ్యతిరేకంగా జరిగిన పని W = n(mgh)
= 1000 × (10 × 9.8 × 0.5 = 49000 J

b) 1 kg క్రొవ్వును సప్లై చేయు యాంత్రిక శక్తి = 3.8

ప్రశ్న 23.
ఒక కుటుంబం 8 kW విద్యుత్ సామర్థ్యాన్ని ఉపయోగిస్తుంది. (a) సౌరశక్తి నేరుగా క్షితిజ సమాంతర తలంపై సగటున ప్రతి చదరపు మీటరుకు 200 W రేటున పతనమవుతుంది. ఈ శక్తిలో 20% విద్యుత్ శక్తిగా ఉపయోగపడితే, 8 kW ని సరఫరా చేయడానికి ఎంత పెద్ద వైశాల్యం ఉన్న తలం అవసరమవుతుంది ? (b) దీన్ని ఒక మాదిరి ఇంటి పైకప్పు వైశాల్యంతో పోల్చండి.
సాధన:
‘A’ sq.m వైశాల్యంను తీసుకుందాము.
∴ మొత్తం సామర్థ్యం = 200A
ఉపయోగపడిన విద్యుతశక్తి / sec = \(\frac{20}{100}\)
= 8KW = 40A = 8000 (watt)
∴ A = \(\frac{8000}{40}\) = 200 sq.m
250 sq.mt గల ఇంటికప్పు వైశాల్యంతో, ఈ వైశాల్యంను పోల్చవచ్చును.

ప్రశ్న 24.
0.012 kg ద్రవ్యరాశి కలిగిన బుల్లెట్, 70 ms^-1 క్షితిజ సమాంతర వడితో 0.4 kg ద్రవ్యరాశి ఉన్న చెక్క దిమ్మెను ఢీకొని చెక్క దిమ్మె పరంగా తక్షణం విరామంలోకి వచ్చింది. ఈ దిమ్మెను సన్నని తీగల ద్వారా లోకప్పు (ceiling) నుంచి వేలాడదీశారు. చెక్క దిమ్మె పైకి లేచే ఎత్తును లెక్కించండి. దిమ్మెలో ఉత్పన్నమయ్యే ఉష్ణాన్ని కూడా లెక్కించండి.
సాధన:
m₁ = 0.012kg. u₁ = 70 m/s
m₂ = 0.4 kg, u₂ = 0
దిమ్మె సాపేక్షంగా బుల్లెట్ విరామ స్థితికి వచ్చును. రెండు ఒకే ఒక వస్తువుగా ప్రవర్తించును. సంయోగము పొందు వేగం’ V ను తీసుకుందాము.

రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమమును అనువర్తించగా, (m₁ + m₂)v
= m₁u₁ + m₂u₂ = m₁u₁

ప్రశ్న 25.
ఘర్షణ లేని వాలుగా ఉన్న రెండు జాడ (track) లపై (పటం) రెండు రాళ్ళు నిశ్చల స్థితి నుంచి, A బిందువు వద్ద నుంచి, వేరువేరుగా జారుతున్నాయి. (ఒక వైపు వాలు క్రమంగా పెరిగి రెండోవైపు నిటారుగా ఉండి A వద్ద కలుసుకొంటున్నాయి.) రెండు రాళ్ళు అడుగు భాగానికి ఒకేసారి చేరుకొంటాయా? ఒకే వడితో చేరుకొంటాయా? వివరించండి. θ₁ = 30°, θ₁ = 60°, h = 10 m అయితే ఈ రెండు రాళ్ళు అడుగు భాగానికి చేరడానికి పట్టే కాలాలు, అవి పొందిన వడులు ఎంత?

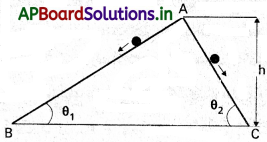
సాధన:
OA మరియు OBలు రెండు నున్నని తలాలు. అవి క్షితిజ సమాంతరంతో చేయు కోణాలు ∠θ₁, మరియు ∠θ₁.
రెండు తలాల ఎత్తులు సమానం. కావున రెండు రాయిలు అడుగునకు ఒకేవడితో చేరును.
∴ P.E = K.E
mgh = \(\frac{1}{2}\)mv₁²= \(\frac{1}{2}\)mv₂²
∴ v₁ = v₂
పటం నుండి, రెండు దిమ్మెల త్వరణాలు

రెండవరాయి తక్కువకాలంలో అడుగునకు, మొదటిరాయి కన్నా ముందుగా చేరును.

ప్రశ్న 26.
ఘర్షణ ఉన్న వాలు తలంపై ఉన్న 1 kg దిమ్మెను 100 N m^-1 స్ప్రింగ్ స్థిరాంకం కలిగిన స్ప్రింగ్తో పటం లో చూపించిన విధంగా కలిపారు. సాగదీయని స్థితిలో స్ప్రింగ్ ఉన్నప్పుడు దిమ్మెను నిశ్చల స్థితి నుంచి విడిచిపెట్టారు. దిమ్మె విరామానికి వచ్చే ముందు వాలు తలంపై 10 cm దూరం కదిలింది. వాలు తలానికి, దిమ్మెను మధ్య ఉండే ఘర్షణ గుణకాన్ని కనుక్కోండి. స్ప్రింగ్ ద్రవ్యరాశి ఉపేక్షించేటట్లుగా ఉన్నదని, అలాగే కప్పీ ఘర్షణ లేనిదని ఊహించండి.

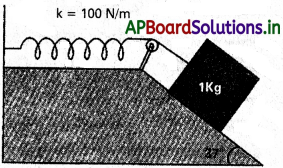
సాధన:
పటం నుండి స్పష్టంగా,
R = mg cosθ
F = µR = µmg cosθ
వాలుతలం క్రింది దిశలో దిమ్మెపై పనిచేయు నికర బలం
= mg sin θ – F = mg sin θ – µ mg cos θ
= mg (sin – µ cos θ)
ప్రయాణించు దూరం, x = 10cm = 0.1m.
సమతాస్థితిలో, జరిగిన పని = సాగదీసిన స్ప్రింగ్ P.E
mg (sin θ – µ cos θ) x = \(\frac{1}{2}\)kx²
2mg (sin θ – µ cos θ) = Kx
2 × 1 × 10 (sin 37° – μ cos 37°) = 100 × 0.1
20(0.601 μ.0.798) = 10
∴ μ = 0.126

ప్రశ్న 27.
7 m s^-1 ఏకరీతి వడితో కిందికి చలిస్తున్న లిఫ్ట్ లో కప్పు (ceiling) నుంచి 0.3 kg ద్రవ్యరాశి ఉన్న బోల్డ్ కిందకు పడింది. ఇది లిఫ్ట్ నేలను ఢీకొని లేవలేదు. లిఫ్ట్ పొడవు = 3 m ఈ అభిఘాతంలో ఉత్పన్నమయ్యే ఉష్ణం ఎంత? లిఫ్ట్ నిశ్చలంగా ఉంటే మీ సమాధానం మారుతుందా?
సాధన:
m = 0.3kg, v = 7 m/s,
h ఎలివేటర్ పొడవు = 3m
ఎలివేటర్ దృష్ట్యా బంతి సాపేక్ష వేగం సున్నా.
అభిఘాతంలో బంతి స్థితిజ శక్తి, ఉష్ణశక్తిగా మారును.
వెలువడు ఉష్ణం పరిమాణం బంతి కోల్పోయిన P.E = mgh 0.3 × 9.8 × 3 = 8.82 J.
ఎలివేటర్ దృష్ట్యా బంతి సాపేక్ష వేగం సున్నా.

ప్రశ్న 28.
ఘర్షణ లేని జాడ (track) పై 200 kg ద్రవ్యరాశి ఉన్న ట్రాలీ 36 km / h ఏకరీతి వడితో చలిస్తుంది. 20 kg ద్రవ్యరాశి ఉన్న పిల్లవాడు ట్రాలీ పై ఒక చివర నుంచి రెండవ చివరకు (10 m దూరం) ట్రాలీకి సాపేక్షంగా, దాని చలన దిశకు వ్యతిరేకంగా 4 m s^-1 వడితో పరిగెత్తుతూ ట్రాలీ నుంచి గెంతాడు. ట్రాలీ తుది వడి ఎంత? పిల్లవాడు పరిగెత్తడం ప్రారంభించిన క్షణం నుంచి ట్రాలీ ఎంత దూరం చలించింది?
సాధన:
ట్రాలీ ద్రవ్యరాశి, m₁ = 200 kg
ట్రాలీ వడి V = 36 km/h = 10 m/s
పిల్లవాని ద్రవ్యరాశి, m₂ = 20 kg
పిల్లవాడు పరుగెత్తకముందు, వ్యవస్థ ద్రవ్యవేగం
P₁ = (m₁ + m₂)v = (200 + 20)10
= 2200kg ms^-1.

పిల్లవాడు, ట్రాలీకి వ్యతిరేఖ దిశలో 4 m/s వేగంతో
పరుగెత్తాడని భావిద్దాం. భూమి సాపేక్షంగా ట్రాలీ తుది వేగం v¹.
భూమి సాపేక్షంగా పిల్లవాని వడి = (v¹ – 4)

∴ పిల్లవాడు పరిగెత్తితే, వ్యవస్థ ద్రవ్యవేగం,
P₂ = 200v¹ + 20 (v¹ – 4) = 220v¹ – 80
వ్యవస్థపై బాహ్య బలం పనిచేయకపోతే,
∴ P₂ = P₁
220v¹ – 80 = 2200
=220v¹ = 2200 + 80 = 2280
v¹ = \(\frac{2280}{220}\) = 10.36 ms^-1

ట్రాలీపై 10m దూరం పరుగెత్తుటకు పిల్లవానికి పట్టుకాలం,
t = \(\frac{10m}{4ms^{-1}}\) = 2.5 s
ఈ కాలంలో ట్రాలీ ప్రయాణించు దూరం = ట్రాలీవేగం × కాలం = 10.36 × 2.5 = 25.9 m

ప్రశ్న 29.
కింద ఇచ్చిన స్థితిజ శక్తి గ్రాఫ్ వక్రాల్లో ఏవి రెండు బిలియర్డ్ బంతుల మధ్య స్థితిస్థాపక అభిఘాతాలను వివరించలేవు? బంతుల కేంద్రాల కేంద్రాల మధ్య దూరం r.

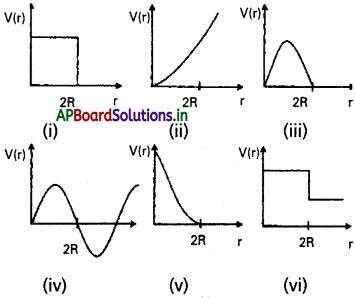
సాధన:
రెండు ద్రవ్యరాశుల వ్యవస్థ స్థితిజశక్తి, వాని మధ్యదూరం (r)నకు విలోమానుపాతంలో ఉండును. i.e, v(r) α \(\frac{1}{r}\) రెండు బిలియర్డ్ బంతులు ఒకదానితో ఒకటి స్పృశించు కుంటున్నప్పుడు, P.E సున్నా i. e., r = R + R = 2R వద్ద ; v(r) = 0.

ఇచ్చిన గ్రాఫ్లలో, వక్రం (v) రెండు నిబంధనలను సంతృప్తి పరుచును. మిగిలిన అన్ని గ్రాఫ్లు, రెండు బిలియర్డ్ బంతుల స్థితిస్థాపక అభిఘాతంను వివరించవు.

ప్రశ్న 30.
నిశ్చల స్థితిలో ఉన్న స్వేచ్ఛా న్యూట్రాన్ క్షీణతను. పరిగణించండి : n → p + e^– ఈ రకమైన రెండు వస్తువుల క్షీణత స్థిరమైన శక్తి ఉన్న ఒక ఎలక్ట్రాను కచ్చితంగా ఇవ్వాలని, అందువల్ల న్యూట్రాన్ లేదా కేంద్రకం యొక్క β-క్షీణతలో కనిపించిన అవిచ్చిన్న శక్తి పంపిణీని వివరించలేక పోతుందని చూపండి.

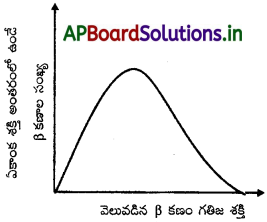
(సూచన : ఈ అభ్యాసం యొక్క సరళమైన ఫలితం ఏమంటే β-క్షీణతలో ఏర్పడే ఉత్పన్నాలలో మూడవ కణం ఉనికిని ఊహించడానికి W. పౌలి ప్రతిపాదించిన అనేక వాదనలలో ఇది ఒకటి. ఈ కణం న్యూట్రినో అని తెలిసింది. ఈ కణం స్వభావజ (intrinsic) స్పిన్^1/2 (e–, p లేదా n వలె) కలిగి, తటస్థంగా ఉండి (ఆవేశరహిత), ద్రవ్యరాశి లేకపోవడం గాని లేదా అతి స్వల్ప ద్రవ్యరాశి కలిగి (ఎలక్ట్రాన్ ద్రవ్యరాశితో పోలిస్తే) ఉంటుందని, ద్రవ్యంతో బలహీనంగా చర్యనొందుతుందని ఇప్పుడు తెలుసుకొన్నాం. కచ్చితమైన న్యూట్రాన్ క్షీణత ప్రక్రియ కింది విధంగా ఉంటుంది : n → p + e^– + v
సాధన:
విఘటన ప్రక్రియలో, n → p + e
ఎలక్ట్రాన్ శక్తి (∆m)c² కు సమానము.
ఇచ్చట ∆m = ద్రవ్యరాశి లోపం = న్యూట్రాన్ ద్రవ్యరాశి – ప్రొటాన్ మరియు – ఎలక్ట్రాన్ ద్రవ్యరాశి. ఇది స్థిరం. న్యూట్రాన్ లేక కేంద్రకము β-విఘటనంలో అవిచ్ఛిన్న శక్తి వితరణను, ఈ రకం విఘటనను వివరించదు. న్యూట్రాన్ సరైన విఘటన ప్రక్రియ n p + e^– + v.

సాధించిన సమస్యలు (Solved Problems)

ప్రశ్న 1.
F = (3\(\hat{\mathbf{i}}\) +4\(\hat{\mathbf{j}}\) – 5\(\hat{\mathbf{k}}\)) ప్రమాణాలు స్థానభ్రంశం d = (5\(\hat{\mathbf{i}}\) + 4\(\hat{\mathbf{j}}\) + 3\(\hat{\mathbf{k}}\)) ప్రమాణాలు అయితే వాటి మధ్య కోణాన్ని, d సదిశ దిశలో F విక్షేపాన్ని కనుక్కోండి.
సాధన:
F.d = F_xd_x + F_yd_y + F_zd_z = 3(5) + 4(4) + (-5) (3) = 16 ప్రమాణాలు
∴ F.d = F d cos θ = 16 ప్రమాణాలు
ఇప్పుడు F.F = F² – F_x² + F_y² + F_z²
9 + 16 + 25 = 50 ప్రమాణాలు
d.d = d² = d_x² + d_y² + d_z²·
25 + 16 + 9 = 50 ప్రమాణాలు

ప్రశ్న 2.
వాన నీటి బిందువులు పడేటప్పుడు కిందకు పనిచేసే గురుత్వాకర్షణ బలం, దీన్ని వ్యతిరేకించే నిరోధక బలాల ప్రభావం ఉంటుందని మనకు బాగా తెలుసు. నిరోధక బలం వాన నీటి బిందువు వేగానికి అనులోమానుపాతంలో ఉంటుంది. దీని గురించి నిర్ధారించవలసి ఉంది. 1.00 g ద్రవ్యరాశి ఉన్న నీటి బిందువు 1.00 km ఎత్తు నుంచి కిందకు పడుతుందనుకోండి. అది 50.0 ms వడితో నేలను తాకింది. దానిపై (a) గురుత్వాకర్షణ బలం వల్ల జరిగిన పని ఎంత? (b) తెలియని నిరోధక బలం వల్ల జరిగిన పని ఎంత?
సాధన:
(a) నీటి బిందువు గతిజశక్తిలో మార్పు
∆K = \(\frac{1}{2}\) mv² – 0
= \(\frac{1}{2}\) × 10^-3 × 50 × 50 = 1.25 J

ఇక్కడ నీటి బిందువు ప్రారంభంలో నిశ్చలస్థితిలో ఉందని ఊహించడమైంది.
పని, శక్తి, సామర్థ్యం
g విలువ 10 m/s× తో స్థిరంగా ఉంటుందని ఊహిస్తే, గురుత్వాకర్షణ బలం వల్ల జరిగిన పని
W_g = mgh = 10^-3 × 10 × 10³ = 10.0 J

(b) పని-శక్తి సిద్ధాంతం నుంచి
∆K = W_g + W_r
ఇక్కడ W_r అనేది వాన నీటి బిందువుపై నిరోధక బలం వల్ల జరిగిన పని

W_r = ∆K – W_g = 1.25 – 10 = – 8.75 J
W_r విలువ రుణాత్మకం

ప్రశ్న 3.
సైకిల్పై ప్రయాణిస్తున్న వ్యక్తి, బ్రేకు వేసినప్పుడు 10 m దూరం జారుతూ ఆగాడు. ఈ ప్రక్రియలో రోడ్డు వల్ల సైకిల్ గమనానికి వ్యతిరేక దిశలో, సైకిల్పై పనిచేసే బలం 200 N. (a) సైకిల్పై రోడ్డు ఎంత పని చేస్తుంది? (b) రోడ్డుపై సైకిల్ ఎంత పని చేస్తుంది?
సాధన:
రోడ్డు సైకిల్పై చేసిన పని అంటే రోడ్డు వల్ల కలిగే నిరోధక బలం (ఘర్షణ బలం) చేసిన పని అవుతుంది.
(a) నిరోధక బలం, స్థానభ్రంశాలు ఒకదానితో ఒకటి చేసే కోణం 180° (π రేడియన్లు) కాబట్టి రోడ్డు వల్ల జరిగిన పని.
= W_r = Fd cos θ 200 × 10 × cos π = -2000 J

ఈ ఋణ పనివల్లనే పని-శక్తి సిద్ధాంతం ప్రకారం సైకిల్ ఆగుతుంది.

(b) న్యూటన్ మూడవ గమన నియమం ప్రకారం సైకిల్ వల్ల సమానం, వ్యతిరేక బలం రోడ్డుపై పనిచేస్తుంది. దీని పరిమాణం 200 N. కాని రోడ్డు ఎటువంటి స్థానభ్రంశం పొందలేదు కాబట్టి రోడ్డుపై సైకిల్ చేసే పని శూన్యం అవుతుంది.

A పై B కలగచేసే బలానికి సమానం, వ్యతిరేక దిశలో B పై A కలగచేసే బలం ఉన్నప్పటికీ (న్యూటన్ మూడవ గమన నియమం) B వల్ల A పై జరిగిన పనికి, B పై A వల్ల జరిగే పని సమానం, వ్యతిరేక దిశలో ఉండవవసరం లేదు.

ప్రశ్న 4.
ప్రక్షేపణాల (ballistics) ప్రదర్శనలో ఒక పోలీసు అధికారి 50.0g ద్రవ్యరాశి ఉన్న బుల్లెట్ను 200 ms^-1 వడితో 2.00 cm మందం ఉన్న ప్లైవుడ్లోకి పేల్చాడు. తొలి గతిజశక్తిలో కేవలం 10% తో మాత్రమే బుల్లెట్ బయటకు వెలువడింది. బయటకు వెలువడిన బుల్లెట్ వడి ఎంత?
సాధన:
బుల్లెట్ తొలి గతిజశక్తి = mv²/2 = 1000 J. దాని తుది గతిజశక్తి 0.1 × 1000 వెలువడిన బుల్లెట్ వడి v_f అయితే,

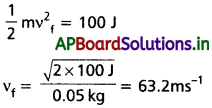
వడి దాదాపు 68% తగ్గింది (90% కాదు).

ప్రశ్న 5.
గరుకుగా ఉన్న రైల్వే ప్లాట్ఫారంపై ఒక స్త్రీ ట్రంకు (trunk) ను తోస్తుంది. 10 m దూరం తోయడానికి 100 N బలం ఆమె ప్రయోగించింది. ఈ తరవాత క్రమంగా ఆమె అలసిపోవడం వల్ల ప్రయోగించిన బలం దూరంతో పాటు రేఖీయంగా తగ్గి 50 N అయ్యింది. ట్రంకు కదిలిన మొత్తం దూరం 20m. స్త్రీ ప్రయోగించిన బలం, ఘర్షణ బలం 50 N లకు, స్థానభ్రంశానికి గ్రాఫ్ గీయండి. ఈ రెండు బలాలు 20m దూరంలో చేసిన పనిని లెక్కించండి.
సాధన:

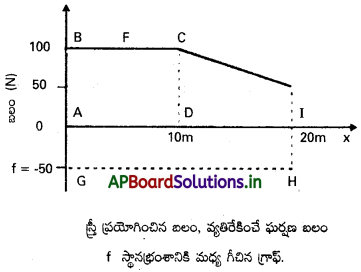
పటంలో ప్రయోగించిన బలం గ్రాఫ్ చూపించడమైంది. x = 20m వద్ద F 50 N (≠ 0). ఘర్షణ బలం f పరిమాణం |f| = 50N గా మనకు ఇవ్వడమైంది. ఇది గమనాన్ని వ్యతిరేకిస్తూ, బలం F కు వ్యతిరేక దిశలో ఉంటుంది. అందువల్ల బలాక్షానికి రుణ దిశలో చూపించడమైంది. స్త్రీ చేసిన పని W_F అయితే,
W_F = ABCD దీర్ఘచతురస్ర వైశాల్యం + CEID సమలంబ చతుర్భుజం వైశాల్యం

W_F = 100 × 10 + \(\frac{1}{2}\)(100 + 50) × 10
= 1000 + 750 = 1750 J

ఘర్షణ బలం చేసిన పని W. అయితే,
W_f → AGHI దీర్ఘచతురస్ర వైశాల్యం
W_f = (-50) × 20 = -1000 J
బల అక్షం రుణదిశవైపు ఉన్న వైశాల్యం రుణ సంజ్ఞను కలిగి ఉంటుంది.

ప్రశ్న 6.
ద్రవ్యరాశి m = 1 kg ఉన్న దిమ్మె క్షితిజ సమాంతర తలంపై vⁱ = 2ms^-1 వడితో కదులుతూ x = 0.10 m నుంచి x = 2.01 m వరకు విస్తరించి ఉన్న గరుకు ప్రదేశంలోకి ప్రవేశించింది. ఈ వ్యాప్తిలో చలనానికి వ్యతిరేకంగా పనిచేసే బలం F_r, x కు విలోమానుపాతంలో ఉంటుంది.
F_r = \(\frac{-k}{x}\)0.1 < x < 2.01 m వద్ద
= 0 x < 0.1 m, x > 2.01 m వద్ద
ఇక్కడ k = 0.5J గరుకు ప్రదేశాన్ని దాటిన తరవాత దిమ్మె తుది గతిజశక్తి, వడి v_f ఎంత?
సాధన:

సహజ సంవర్గమానం. అంతేకాని 10 ఆధారం కలిగిన సంవర్గమానం కాదు అని గుర్తించాలి [lnX = log_e X = 2.303 log₁₀ X].

ప్రశ్న 7.
L పొడవు ఉన్న తేలికైన దారంతో m ద్రవ్యరాశి ఉన్న గోళం వేలాడదీయడమైంది. నిమ్నతమ బిందువు A వద్ద దానికి క్షితిజ సమాంతర వేగం v_o ఇవ్వడం వల్ల అది క్షితిజ లంబ తలంలో అర్థవృత్తాన్ని పూర్తిచేసి ఊర్థ్వతమ బిందువు Cని చేరింది. Cని చేరినప్పుడు మాత్రమే దారం వదులయింది (slack). ఇది పటంలో చూపించడమైంది. (i) v_o; (ii) B, C ల వద్ద వడి; (iii) B, C ల వద్ద గతిజ శక్తుల నిష్పత్తు (K_B/K_C) లకు సమీకరణాలను రాబట్టండి. C ని చేరిన తరువాత గోళం ప్రక్షేపక మార్గం స్వభావంపై వ్యాఖ్యానించండి.

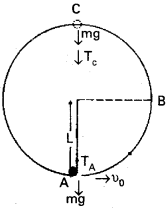
సాధన:
i) గోళంపై రెండు బాహ్య బలాలు పనిచేస్తుంటాయి.
గురుత్వం, దారంలోని తన్యత (T). దారంలో తన్యత చేసిన పని శూన్యం. ఎందుకంటే గోళం స్థానభ్రంశం ఎప్పుడూ దారానికి లంబంగా ఉంటుంది. అందువల్ల గోళం స్థితిజశక్తి, గురుత్వబలంతో మాత్రమే సంబంధం కలిగి ఉంటుంది. వ్యవస్థ మొత్తం యాంత్రిక శక్తి E నిత్యత్వంగా ఉంటుంది. నిమ్నతమ బిందువు A వద్ద వ్యవస్థ స్థితిజ శక్తిని సున్నాగా తీసుకొంటాం. అందువల్ల
A వద్ద :
E = \(\frac{1}{2}\)mv²₀ …………… (1)
T_A – mg = \(\frac{mv^{2}_{0}}{L}\) [న్యూటన్ రెండవ నియమం]

A వద్ద దారంలో తన్యత T_A దారంలో తన్యత (T_c) శూన్యమవుతుంది. కాబట్టి ఊర్థ్వతమ బిందువు వద్ద దారం వదులవుతుంది.
అందువల్ల C వద్ద
E = \(\frac{1}{2}\)mv²_e + 2mgL …………… (2)
mg = \(\frac{mv^{2}_{e}}{L}\) [న్యూటన్ రెండవ నియమం] .. (3)
ఇక్కడ v_cఅనేది C వద్ద వడి సమీకరణాలు (2), (3) ల నుంచి
E = \(\frac{5}{2}\)mgL
దీనిని A వద్ద శక్తితో సమానం చేస్తే,

C బిందువు వద్ద దారం వదులవుతుంది, గోళం వేగం ఎడమవైపు క్షితిజ సమాంతరంగా ఉంటుంది. ఈ క్షణంలో దారం తెగిపోతే, గోళం క్షితిజ సమాంతర ప్రక్షేపం వంటి ప్రక్షేపక చలనం చేస్తుంది. ఇది శిఖరం పైన ఉన్న రాయిని క్షితిజ సమాంతరంగా తన్నినప్పుడు అది పొందే పథంలాంటిది. అలా తెగకుంటే, వృత్తాకార పథంలో గోళం పూర్తి భ్రమణం చేస్తుంది.

ప్రశ్న 8.
కారు ప్రమాదాలను పోలి ఉండే విధంగా కారు తయారీదార్లు వివిధ స్ప్రింగ్ స్థిరాంకాలు కలిగిన స్ప్రింగ్లతో గమనంలో ఉన్న కార్ల అభిఘాతాలను అధ్యయనం చేస్తారు. అలాంటి ఒక పోలికను పరిగణిద్దాం. 1000 kg ద్రవ్యరాశి కలిగిన కారు 18.0 km / h వడితో నున్నటి రోడ్డుపై చలిస్తూ 6.25 × 10³ N m^-1. స్ప్రింగ్ స్థిరాంకం ఉన్న క్షితిజ సమాంతరంగా తగిలించిన స్ప్రింగ్ను ఢీకొంది. స్ప్రింగ్ చెందే గరిష్ట సంపీడనం ఎంత?
సాధన:
స్ప్రింగ్ గరిష్ఠ సంపీడనం చెందినప్పుడు కారు గతిజశక్తి పూర్తిగా స్ప్రింగ్ స్థితిజ శక్తిగా మారుతుంది.
గమనంతో ఉన్న కారు గతిజ శక్తి
K = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × 10³ × 5 × 5
K = 1.25 × 10⁴ J

ఇక్కడ 18 km h^-1ను 5ms^-1 గా మార్చుడమైంది. [36 km h-^-1 = 10 ms^-1 అని గుర్తుంచుకోవడం ఉపయోగకరం.] యాంత్రిక శక్తి నిత్యత్వ నియమం ప్రకారం స్ప్రింగ్ గరిష్ట సంపీడనం X_m వద్ద స్ప్రింగ్ స్థితిజ శక్తి V గమనంలో ఉన్న కారు గతిజ శక్తి Kకి సమానం.
V = \(\frac{1}{2}\)k x²_m = 1.25 × 10⁴ J
దీని నుంచి x_m = 2.00 m వస్తుంది.

ఇక్కడ మనం స్ప్రింగ్ను ద్రవ్యరాశి లేనిదిగా, తలానికి ఉపేక్షించదగిన ఘర్షణ ఉందని పరిగణించడమైంది. ఇది ఒక ఆదర్శ పరిస్థితి అని గమనించవచ్చు.

నిత్యత్వ బలాలపై కొన్ని సూచనలు చేసి ఈ విభాగాన్ని ముగించవచ్చు.

i) పై చర్యల్లో కాలం గురించి సమాచారం లేదు. పైన తీసుకొన్న ఉదాహరణలో సంపీడనాన్ని మనం లెక్కించవచ్చు కాని సంపీడనం జరిగిన కాలాన్ని లెక్కించలేం. కాలానికి సంబంధించిన సమాచారం న్యూటన్ రెండవ గమన నియమాన్నుంచి తెలుసు కోవచ్చు.

ii) అన్ని బలాలు నిత్యత్వ బలాలు కావు. ఉదాహరణకు ఘర్షణ బలం అనిత్యత్వ బలం. ఈ సందర్భానికి శక్తి నిత్యత్వ నియమాన్ని మార్పు చేయవలసి ఉంటుంది. దీన్ని ఉదాహరణ 9లో వివరించడమైంది.

iii) స్థితిజ శక్తి సున్నా విలువ అనేది అనియతమైనది (arbitrary) ఇది సౌలభ్యం కోసం ఏర్పరిచింది. స్ప్రింగ్ బలానికి x = 0 వద్ద V(x) తీసుకొన్నాం. అంటే సాగదీయని స్ప్రింగ్ సున్నా స్థితిజ శక్తిని కలిగి ఉంటుంది. స్థిర గురుత్వ బలం mgకి -భూమి ఉపరితలంపై V = 0 అని తీసుకొంటాం. తరువాతి అధ్యాయంలో విశ్వగురుత్వ నియమం వల్ల ఏర్పడే బలం సంబంధంలో గురుత్వ జనకం నుంచి అనంత దూరం వద్ద స్థితిజ శక్తిని సున్నాగా ఉత్తమంగా నిర్వచించడమైంది. ఏది ఏమైనా ఒకసారి స్థితిజ శక్తి విలువను సున్నాగా స్థిరీకరిస్తే దాన్ని అదే విధంగా తరవాత చర్చలో కొనసాగించాలి. అంతేగాని మధ్యలో ఈ విలువను మార్చరాదు.

ప్రశ్న 9.
8వ ఉదాహరణలో ఘర్షణ గుణకం µ విలువ 0.5 గా తీసుకొని స్ప్రింగ్ గరిష్ట సంపీడనాన్ని లెక్కించండి.
సాధన:

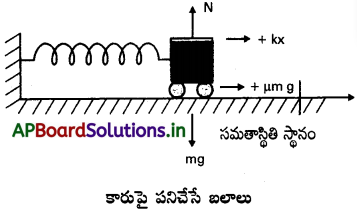
పటంలో చూపినట్లు ఘర్షణ ఉన్నప్పుడు ఘర్షణ బలం, స్ప్రింగ్ బలం రెండూ స్ప్రింగ్ సంపీడనాన్ని వ్యతిరేకిస్తాయి.

యాంత్రిక శక్తి నిత్యత్వ నియమం కంటే పని-శక్తి సిద్ధాంతాన్ని ఇక్కడ ఉపయోగిస్తాం.
గతిజ శక్తిలోని మార్పు

ఇప్పుడు µmg = 0.5 × 10³ × 10 5 × 10³ N
(g = 10.0 ms^-2 గా తీసుకోండి]. పై సమీకరణాన్ని మనకు తెలియని x_m తో కూడిన ఒక వర్గ సమీకరణంగా మార్చవచ్చు.

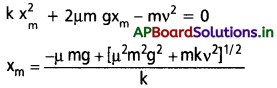
ఇక్కడ x_m ధనాత్మకం కాబట్టి ధన వర్గ మూలం తీసుకొంటాం. పై సమీకరణంలో విలువలను ప్రతిక్షేపిస్తే,
x_m = 1.35 m
మనం ఊహించినట్లే ఇది ఉదాహరణ 8 లో వచ్చిన విలువ కంటే ఎక్కువ.

నిత్యత్వ బలం F_c, అనిత్యత్వ బలం F_nc అనే రెండు బలాలు వస్తువుపై పనిచేసినప్పుడు యాంత్రిక శక్తి నిత్యత్వ ‘నియమాన్ని మార్చవలసి ఉంటుంది. పని శక్తి సిద్ధాంతం నుంచి
(F_c + F_nc) ∆x = ∆K
కాని F_c ∆x = – ΔV
అందువల్ల, ∆(K + V) = Fnc ∆x
∆E = F_nc Δx

ఇక్కడ E మొత్తం యాంత్రిక శక్తి, మొత్తం పథంలో ఈ సూత్రం కింది రూపాన్ని పొందుతుంది.
E_f – E_i = W_nc

ఇక్కడ W_nc అనేది ఆ పథంలో అనిత్యత్వ బలం చేసిన మొత్తం పని. నిత్యత్వ బలంలాగా కాకుండా i నుంచి f కు గల నిర్ణీత పథంపై Wnc ఆధారపడి ఉంటుంది.

ప్రశ్న 10.
(a) DNA లో ఒక బంధాన్ని విచ్ఛిన్నం చేయడానికి అవసరమయ్యే శక్తిని eV లలో (b) గాలి అణువు గతిజ శక్తి (10^-21J) ని eV లలో; (c) ఒక పెద్ద వ్యక్తి రోజూ తీసుకొనే ఆహారాన్ని కిలో కెలరీలలో వ్యక్తపరచండి.
సాధన:
(a) DNA లో ఒక బంధాన్ని విచ్ఛిన్నం చేయడానికి అవసరమయ్యే శక్తి

సాధారణంగా వార్తా పత్రికలు, మాగజైన్లు (magazines) ఒక తప్పును పదే పదే వల్లిస్తూ ఉంటాయి. దానిని మనం ఇక్కడ చూద్దాం. ఆహారం విలువలను కెలరీలలో చెప్పి మనం తీసుకొనే ఆహారం విలువ 2400 కెలరీల కంటే తక్కువగా ఉండాలని సూచిస్తాయి. వాళ్ళు చెప్పవలసినది కిలో కెలరీలు (kcal) అంతే కానీ కెలరీలు కాదు. రోజుకు 2400 కెలరీల ఆహారం తీసుకొనే వ్యక్తి త్వరలోనే ఆకలితో మరణిస్తాడు. ఒక ఆహారం కెలరి అంటే 1 kcal.

ప్రశ్న 11.
2ms^-1 స్థిరవడితో పైకి చలిస్తున్న లిఫ్ట్ గరిష్ఠంగా 1800 kg (లిఫ్ట్ + ప్రయాణీకులు) బరువును తీసుకొనివెళ్ళగలదు. ఈ చలనాన్ని వ్యతిరేకిస్తున్న ఘర్షణ బలం 4000 N. మోటారు లిఫ్ట్కు అందించవలసిన కనీస సామర్ధ్యాన్ని వాట్లలో, అశ్వసామర్ధ్యాలలో కనుక్కోండి.
సాధన:
లిప్పై కిందకు పనిచేసే బలం
F = mg + F_f = (1800 × 10) + 4000 = 22000 N
ఈ బలాన్ని తుల్యం చేయడానికి సరిపడే సామర్థ్యాన్ని మోటారు అందించాలి. అందువల్ల.
P = F.v = 22000 × 2 = 44000 W

ప్రశ్న 12.
న్యూట్రాన్ల వడి క్రమంగా తగ్గడం : న్యూక్లియర్ రియాక్టర్లో న్యూట్రాన్ల అధిక వడి (సుమారు 10⁷ms^-1)10³ ms^-1 కు క్రమంగా తగ్గితేనే అవి ²³⁵₉₂U ఐసోటోప్ చర్యనొంది దానిని విచ్ఛిత్తి గావించడానికి అధిక సంభావ్యత కలిగి ఉంటుంది. న్యూట్రాన్ ద్రవ్యరాశి కంటే కొద్ది రెట్లు అధిక ద్రవ్యరాశి కలిగిన డ్యుటీరియం లేదా కార్బన్ వంటి తేలిక కేంద్రకాలతో న్యూట్రాన్ స్థితిస్థాపక అభిఘాతం జరిపినప్పుడు దాని (న్యూట్రాన్) గతిజ శక్తిలో ఎక్కువ భాగం నష్టపోతుందని చూపండి. తేలిక కేంద్రకాలు సాధారణంగా భారజలం (D₂O) లేదా గ్రాఫైట్ లతో తయారయి ఉంటాయి. వీటిని మితకారి (moderator) అంటారు.
సాధన:
న్యూట్రాన్ తొలి గతిజ శక్తి

మితకారి కేంద్రకాలు పొందే గతిజ శక్తి భాగం K_2f/K_1i అయితే,
f₂ = 1 – f₁ (స్థితిస్థాపక అభిఘాతం)

ఫలితాన్ని సరిచూడవచ్చు.
డ్యుటీరియం కేంద్రకానికి m₂ = 2m₁ కాబట్టి f₂ = 8/9 అయితే f₁ = 1/9 అని వస్తుంది. సుమారు 90% న్యూట్రాన్ల శక్తి డ్యుటీరియంకు బదిలీ అవుతుంది. కార్బన క్కు f₁ = 71.6%, f₂ = 28.4%. వాస్తవంగా ఏకమితీయ అభిఘాతాలు చాలా అరుదు కాబట్టి ఈ సంఖ్య తక్కువగా ఉంటుంది.

ప్రశ్న 13.
సమాన ద్రవ్యరాశులు m₁ = m₂ ఉన్న రెండు బిలియర్డ్ బంతుల మధ్య పటంలో చూపినట్లు అభిఘాతాన్ని పరిగణిద్దాం. మొదటి బంతిని క్యూ (cue) అని రెండవ బంతిని లక్ష్యమని అంటారు. బిలియర్డ్ ఆటగాడు లక్ష్యంగా ఉన్న బంతిని 37° కోణంతో మూలలో ఉన్న పాకెట్ (pocket) లో వేయాలనుకొంటాడు. అభిఘాతం స్థితిస్థాపకమని, ఘర్షణభ్రమణ చలనాలు ముఖ్యం కాదని ఊహించండి. θ₁ ను రాబట్టండి.

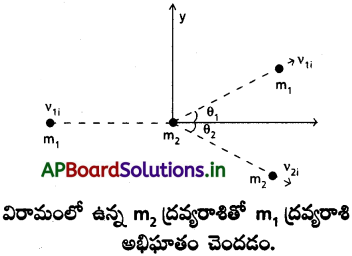
సాధన:
ద్రవ్యవేగ నిత్యత్వం నుంచి ద్రవ్యరాశులు సమానం కాబట్టి
v_1i = v_1f + v_2f
లేదా v_1i² = (v_1f + v_2f) × (v_1f + v_2f)
= v_1f² + _2f² + 2v_1fv_2f
= {v_1f² + v_2f² + 2v_1fv_2f cos (θ₁ + 37} ………. (1)

అభిఘాతం స్థితిస్థాపకం m₁ = m₂ కాబట్టి గతిజ శక్తి నిత్యత్వం నుంచి
v_1i² = v_1f² + _2f² …….. (2)
సమీకరణాలు (1); (2) పోలిస్తే,
cos (θ₁ + 37°) = 0 వస్తుంది.
లేదా θ₁ + 37° = 90°
అందువల్ల, θ₁ = 53°

రెండు ద్రవ్యరాశులు సమానంగా ఉండి ఒకటి విరామంలో, రెండవది గమనంలో ఉంటూ అనుస్పృశ (glancing) స్థితిస్థాపక అభిఘాతం జరిపితే, అభిఘాతం తరవాత అవి ఒకదానికొకటి లంబంగా ఉండేటట్లు చలిస్తాయని పై ఫలితం నిరూపిస్తుంది.

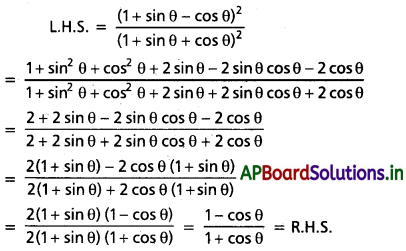
Students can go through AP Inter 1st Year Commerce Notes 3rd Lesson Forms of Business Organization will help students in revising the entire concepts quickly.

AP Inter 1st Year Commerce Notes 3rd Lesson Forms of Business Organization

→ Business is one of the human economic activities. Profit is a consideration of business.

→ Business is an economic entity i.e., an artificial person.

→ Business units may be classified into two types.

1. Noncorporate units
2. Corporate units

→ Sole proprietorship concern is one of the noncorporate units.

→ Each and every business concern must have its own merits and demerits.

→ Sole proprietorship business is owned by only one person and controlled by a single individual.

→ The complete risk in sole proprietorship concern is borne by a sole trader.

→ The sole trade liability is an unlimited liability because the sole proprietorship firm has no separate legal entity.

→ The sole trader and sole proprietorship firms both were the same as per law.

→ To commencement of sole proprietorship firm legal formalities are very less.

→ In sole proprietorship concerns, decisions should be taken by only one person i.e., the sole trader.

→ వ్యాపారానికి సంబంధించిన యాజమాన్య, నిర్వహణ ఏర్పాటును వ్యాపార వ్యవస్థ అంటారు. ఇది వివిధ రూపాలలో ‘ది. వ్యాపార వ్యవస్థల ఎన్నిక వివిధ స్వరూపాల ప్రయోజనాలు, పరిమితుల సమతూకముపై ఆధారపడి ఉం బంది. ఈ ఎంపిక చాలా క్లిష్టమైనది. నియంత్రణ, నష్టభయం, అధికారము మొదలైన అంశాలనాధారముగా ఎంపిక చేయాలి. ఏ సంస్థ అయినా దీర్ఘకాలము కొనసాగాలి అంటే ముందు చూపుతో అనేక సంప్రదింపుల తరువాత సరైన వ్యాపార స్వరూపాన్ని ఎంపికచేసుకోవాలి.

→ సొంత వ్యాపారవ్యవస్థలో ఒకే వ్యక్తి మూలధనాన్ని సమకూర్చి తన సొంత నైపుణ్యం, అనుభవము నిర్వహణలో ఉపయోగించి, తద్వారా వచ్చే ఫలితాలను పూర్తిస్థాయిలో తానే బాధ్యత వహిస్తాడు.

Students can go through AP Inter 1st Year Commerce Notes 2nd Lesson Business Activities will help students in revising the entire concepts quickly.

AP Inter 1st Year Commerce Notes 2nd Lesson Business Activities

→ All business activities are economic activities, a man is engaged in, to earn his livelihood by producing and distributing goods and rendering services.

→ Business may be defined as a human activity directed towards producing or acquiring wealth through buying and selling of goods.

→ Industry refers to the production of consumer goods and capital goods, creating form utility.

→ Commerce is part of the business. It deals with buying and selling goods and services. Commerce is concerned only with the exchange of goods. It includes all those activities which are related to the transfer of goods from the production place to the consumption place.

→ Trade means the purchase and sale of goods with a profit motive. It involves the exchange of goods and services between buyers and sellers.

→ Aids to trade include transport, communication, warehousing, banking, insurance, and advertising.

→ వస్తు సేవల ఉత్పత్తికి సంబంధించిన కార్యకలాపాల సమూహాన్ని పరిశ్రమ అంటారు.

→ పరిశ్రమలను ప్రాథమిక, ప్రజనన, ఉద్భహణ, తయారీ, నిర్మాణ, సేవా పరిశ్రమలుగా విభజించవచ్చు.

→ పారిశ్రామిక ప్రపంచములో వ్యక్తుల మధ్య వస్తువుల పంపిణీ కోసం ఏర్పడిన శ్రమబద్ధమైన వ్యవస్థ వాణిజ్యం.

→ వస్తు మార్పిడిలో గల అవరోధాలను వాటి తొలగింపుకు వాణిజ్యము ముఖ్యమైనది.

→ వస్తువుల కొనుగోలు, అమ్మకాల ప్రక్రియ వర్తకము. దీనిని స్వదేశీ వర్తకము, విదేశీ వర్తకముగా విభజించవచ్చు. స్వదేశీ వర్తకాన్ని టోకు, చిల్లర వర్తకమని, విదేశీ వర్తకాన్ని ఎగుమతి, దిగుమతి, మారు వర్తకముగా విభజించవచ్చును.

→ వర్తక సదుపాయాలు – రవాణా, గిడ్డంగులు, బ్యాంకింగ్ ప్రకటనలు, బీమా, కమ్యూనికేషన్ మొదలైనవి.

Students can go through AP Inter 1st Year Commerce Notes 1st Lesson Concept of Business will help students in revising the entire concepts quickly.

AP Inter 1st Year Commerce Notes 1st Lesson Concept of Business

→ The term business refers to ‘the state of being busy”.

→ Business is one of the human economic activities. Business is an economic activity that involves the regular transfer or exchange of goods and services for earning profit.

→ Business creates utilities by producing and selling goods and services to satisfy human wants.

→ Time, place, and possession of values are created by business enterprises.

→ Every business enterprise has both economic and social objectives.

→ The obligation of any business enterprise is to protect and serve the public interest as they operate within a society.

→ The Business organisations must be responsible to different Interest groups like owners, employees, suppliers, customers, government, etc.

→ ప్రతి వ్యక్తి తన కోర్కెలను సంతృప్తిపరుచుకొనడానికి నిరంతరము శ్రమిస్తాడు. ఫలితముగా మానవ కార్యకలాపాలు ఏర్పడతాయి. వీటిని ఆర్థిక కార్యకలాపాలు అని, ఆర్థికేతర కార్యకలాపాలు అని విభజించవచ్చు.

→ ఆర్థిక కార్యకలాపాలు వృత్తి, ఉద్యోగము, వ్యాపారము. సమర్థవంతమైన వ్యక్తిగత సేవలను అందించే పనులను వృత్తులు అంటారు. ఒప్పందము ప్రకారము యజమాని చెప్పిన పనులను నిర్వహించడాన్ని ఉద్యోగము అంటారు. లాభాన్ని సంపాదించే ఉద్దేశముతో వస్తుసేవల ఉత్పత్తి వినిమయము, పంపిణీలతో ఉండే వ్యాపకాన్ని వ్యాపారము అంటారు.

→ వ్యాపార లక్షణాలలో ప్రయోజనాల కల్పన, వస్తుసేవలతో సంబంధము, పునరావృతము కాకపోవడం, లాభార్జన, నష్టభయం, అనిశ్చిత పరిస్థితి, కళ అనేవి ఉంటాయి.

→ ప్రతి వ్యాపారానికి ఆర్థిక, సామాజిక, మానవ సంబంధిత, జాతీయ లక్ష్యాలు ఉంటాయి.

→ ఆర్థిక లక్ష్యాలలో లాభాల సంపాదన, ఖాతాదారుల సృష్టి నవకల్పన ఉన్నాయి.

→ సామాజిక లక్ష్యాలలో సరైన వస్తువులను సరైన ధరలకు సప్లయి చేయడము, ఉద్యోగులకు చాలినంత ప్రతిఫలం అందజేయడము, సాంఘిక సంక్షేమము, ప్రభుత్వానికి సహకారము, సహజ వనరుల సక్రమ వినియోగము ఉన్నది. 7 మానవ సంబంధిత లక్ష్యాలలో మానవ వనరుల అభివృద్ధి, ప్రజాస్వామ్య నిర్వహణ, శ్రామిక యజమానుల సహకారము ఉన్నాయి.

→ జాతీయ లక్ష్యాలలో వనరుల గరిష్ఠ వినియోగము, జాతీయ గౌరవం, చిన్నతరహా పరిశ్రమల వృద్ధి వెనుకబడిన ప్రాంతాల అభివృద్ధి అనేవి ఉంటాయి.

→ వ్యాపారము సమాజములో అంతర్భాగము అయినందున లాభార్జనతో పాటు సామాజిక సంక్షేమాన్ని గురించి కూడా వ్యాపార సంస్థలు ఆలోచించాలి. దీనినే సామాజిక బాధ్యత అంటారు. యజమానులకు, ఉద్యోగులకు, సప్లయిదారులకు, ప్రభుత్వానికి, సమాజానికి సంబంధించి వ్యాపార సంస్థలకు వేర్వేరు బాధ్యతలు ఉంటాయి.