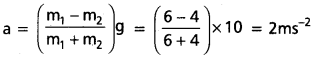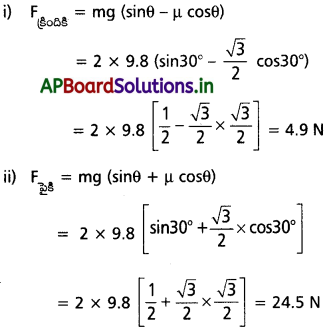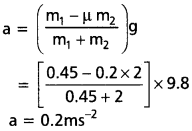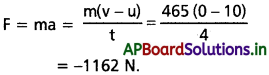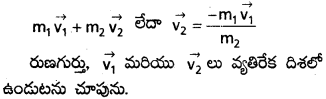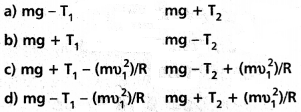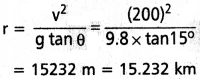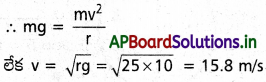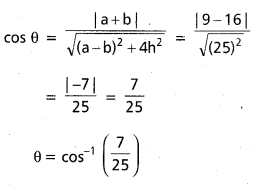Mahesh

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 5th Lesson గమన నియమాలు Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 5th Lesson గమన నియమాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
జఢత్వం అంటే ఏమిటి? జడత్వ కొలతను ఏది ఇస్తుంది?
జవాబు:
జఢత్వం :
ఫలిత బాహ్యబలం ప్రమేయం లేనప్పుడు, నిశ్చల స్థితిలో ఉన్న వస్తువు అదే స్థితిలో ఉండటానికి మరియు ఋజుమార్గంలో గమన స్థితిలో ఉన్న వస్తువు అదే స్థితిలో ఉండటానికి ప్రయత్నించే వస్తు ధర్మాన్ని జఢత్వం అంటారు. ద్రవ్యరాశి, జఢత్వ కొలతను ఇస్తుంది.

ప్రశ్న 2.
న్యూటన్ మూడవ గమన నియమం ప్రకారం ప్రతి బలం సమానం, వ్యతిరేక బలాలతో కూడి ఉన్నప్పుడు గమనం అనేది ఏ విధంగా సాధ్యమవుతుంది?
జవాబు:
వేర్వేరు వస్తువులపై బలం మరియు వ్యతిరేఖ బలంలు పనిచేసినప్పుడు, వస్తువుకు గమనం సాధ్యం.

ప్రశ్న 3.
ఒక తుపాకీ నుంచి బుల్లెట్ను పేల్చినప్పుడు, తుపాకీని వెనకకు నెట్టివేసినట్లు అనిపిస్తుంది. వివరించండి.
జవాబు:
ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం, తుపాకి నుండి బుల్లెట్ను పేల్చితే, తుపాకి ద్రవ్యవేగం, బుల్లెట్ ద్రవ్యవేగంనకు సమానమై, వ్యతిరేఖ దిశలో ఉండును. కావున బుల్లెట్ ముందుకు, తుపాకి వెనుకకు చలించును.

ప్రశ్న 4.
ఒకే గుళ్లను ఉపయోగించినా బరువుగా ఉన్న రైఫిల్ తేలిక రైఫిల్ కంటే తక్కువ వేగంతో వెనకకు వస్తుంది. ఎందువల్ల?
జవాబు:
ద్రవ్యవేగ నిత్యత్వ నియమము ప్రకారం, భారరైఫిల్ ద్రవ్యవేగం = తేలిక రైఫిల్ ద్రవ్యవేగం = గుళ్ళ ద్రవ్యవేగం.
రైఫిల్ వెనుకకు వచ్చు వేగం, V = \(\frac{mu}{M}\)

భారరైఫిల్ ద్రవ్యరాశి (M) ఎక్కువ. కావున వెనుకకు వచ్చు వేగం తక్కువ.

ప్రశ్న 5.
విరామస్థితిలో ఉన్న ఒక బాంబు రెండు ముక్కలుగా పేలితే దాని ముక్కలు వ్యతిరేకదిశలో చలిస్తాయి. వివరించండి.
జవాబు:
రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమము ప్రకారం, Mu = m₁v₁ + m₂v₂
మొట్టమొదటి బాంబు నిశ్చలస్థితిలో ఉంది కాబట్టి u = 0
∴ m₁v₁ + m₂v₂ = 0
m₁v₁ = – m₂v₂

పై సమీకరణములో రుణగుర్తు ముక్కలు వ్యతిరేఖ దిశలో చలించుటను తెలియచేయును.

ప్రశ్న 6.
బలాన్ని నిర్వచించండి. ప్రకృతిలోని ప్రాథమిక బలాలను పేర్కొనండి.
జవాబు:
ఒక వస్తువు విరామస్థితిని లేదా సరళరేఖ వెంబడి సమగమన స్థితిని మార్చే లేదా మార్చడానికి ప్రయత్నించే రాశిని బలం అంటారు. ప్రాథమిక బలాలు మూడు. అవి

1. గురుత్వాకర్షణ బలం,
2. విద్యుదయస్కాంత బలం
3. కేంద్రక బలం
4. బలహీన అంతరచర్య బలం

ప్రశ్న 7.
ఘర్షణ గుణకం విలువ ఒకటి కంటే ఎక్కువగా ఉంటుందా?
జవాబు:
ఘర్షణ బలం ఒకటి కంటే ఎక్కువగా ఉండవచ్చును. కొన్ని ప్రత్యేక సందర్భములలో ఇది సాధ్యము. అవి.

1. తలాలను అధికంగా నునుపుచేసినపుడు అణు అంతర ఆకర్షణ బలాలు అధికమయినపుడు.
2. రెండు తలాలు ఒకదానితో ఒకటి పెనవేసుకున్నపుడు (inter locking) ఘర్షణ గుణకం 1 కంటే ఎక్కువగా ఉండును.

ప్రశ్న 8.
గాలి నిండిన టైర్లు ఉన్న కారు కంటే గాలి లేని టైర్లు ఉన్న కారు తొందరగా ఆగుతుంది. ఎందుకు? [May ’13]
జవాబు:
విరూపణ అధికంగా ఉన్న దొర్లుడు వస్తువులకు దొర్లుడు ఘర్షణ అధికంగా ఉంటుంది. ఇందువలన గాలిలేని టైరు శీఘ్రంగా నిశ్చలస్థితికి వస్తుంది.

ప్రశ్న 9.
గుర్రం చలనంలో ఉన్నప్పటి కంటే, అది బయలుదేరడం ప్రారంభించే సమయంలో ఎక్కువ బలాన్ని ఎందుకు ఉపయోగిస్తుంది? [Mar. 13]
జవాబు:
గుర్రం, బండిని నిశ్చల స్థితిలో నుండి స్థితిక ఘర్షణ బలము విలువ గతిక ఘర్షణబలం కంటే అధికంగా ఉండుట వలన గమనంలోనికి తేవడానికి గరిష్ఠ స్థితిక ఘర్షణ బలాన్ని అధిగమించే బలాన్ని ప్రయోగించవలెను. బండి గమనంలో ఉన్నప్పుడు ఘర్షణ బలం తగ్గుతుంది. కాబట్టి గమనానికి ప్రారంభంలో గుర్రం ఎక్కువ బలంతో బండిని లాగవలసి ఉంటుంది.

ప్రశ్న 10.
వస్తువు భారాన్ని రెట్టింపు చేస్తే ఘర్షణ గుణకం ఏమవుతుంది?
జవాబు:
F α Nకావున వస్తువు భారాన్ని రెట్టింపు చేసిన ఘర్షణబలం కూడా రెట్టింపు అగును.
∴ ఘర్షణ గుణకం = F/N. కావున, దీని విలువ మారడు.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
0.1 kg ద్రవ్యరాశి ఉన్న ఒక రాయిని నిలువుగా పైకి విసిరారు. కింద సందర్భాలలో రాయిపై పనిచేసే నీకర బలం పరిమాణం, దిశను తెలపండి. (a) నిలువుగా పైకి ప్రయాణిస్తున్నప్పుడు, (b) కిందికి ప్రయాణిస్తున్నప్పుడు, (c) గరిష్ఠ ఎత్తు వద్ద, (ఎక్కడైతే క్షణం పాటు రాయి విరామస్థితికి వస్తుందో).
జవాబు:
రాయి ద్రవ్యరాశి, m = 0.1 kg, g = 9.8 ms^-2.
a) నిలువుగా పైకి ప్రయాణిస్తూ ఉన్నప్పుడు : రాయిపై పనిచేసే నికర బలం పరిమాణం
F = |-mg|; F = 0.1 × 9.8 = 0.98N.
నికర బలం దిశ, నిలువుగా పైకి ప్రయాణిస్తున్న దిశలో ఉండును.

b) రాయి కిందికి ప్రయాణిస్తూ ఉన్నప్పుడు : రాయిపై నికరబలం పరిమాణం,
F = mg = 0.1 × 9.8 = 0.98N.
బలం కింది దిశలో ఉండును.

c)గరిష్ఠ ఎత్తు వద్ద ఉన్నప్పుడు : నికరబలం పరిమాణం,
F = mg = 0.1 × 9.8 = 0.98N.
రాయి, గరిష్ఠ ఎత్తు వద్ద ఉన్నప్పుడు దిశ నిర్ణయించలేము.

ప్రశ్న 2.
ద్రవ్యవేగం, ప్రచోదనాలను నిర్వచించండి. రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమాన్ని నిర్వచించి, వివరించండి. ఉదాహరణలు ఇవ్వండి.
జవాబు:
ద్రవ్యవేగము :
ఒక వస్తువు యొక్క ద్రవ్యరాశి మరియు వేగాల లబ్దాన్ని ద్రవ్యవేగం (p) అంటారు.
ద్రవ్యవేగము (p) = mv

ప్రచోదనం :
అతిస్వల్పకాలంలో వస్తువు ద్రవ్యవేగంలో పరిమిత మార్పును కలిగించే అత్యధిక బలాన్ని ప్రచోదన బలం అంటారు. వస్తువు ద్రవ్యవేగంలో పరిమిత మార్పును కలిగించే బలం, కాలాల లబ్ధాన్ని ప్రచోదనం అంటారు.
ప్రచోదనం = బలం × కాలవ్యవధి
= F × t = mat = m\(\frac{(v-u)}{t}\)t = m(v – u)

రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమము :
“ఒక వియుక్త వ్యవస్థపై ఫలిత బాహ్యబలం లేనప్పుడు, అంతర చర్యలు గల కణాల మొత్తం ద్రవ్యవేగం స్థిరము”.

వివరణ :
రెండు నున్నని, భ్రమణరహిత m₁ మరియు m₂ (m₁ > m₂) ద్రవ్యరాశి గల రెండు గోళాలను భావిద్దాం. వాని తొలివేగాలు u₁ మరియు u₂ ముఖాముఖి అభిఘాతం తరువాత వాని వేగాలు v₁ మరియు v₂. రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమము ప్రకారము,

అభిఘాతంనకు ముందు వ్యవస్థ ద్రవ్యవేగం = అభిఘాతం తరువాత వ్యవస్థ ద్రవ్యవేగం
i.e., m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

ఉదాహరణలు : 1) రాకెట్ చలనం 2) బుల్లెట్-గన్ (తుపాకి) చలనం.

ప్రశ్న 3.
మోటారు సైకిళ్ళు, కార్లకు షాక్ అబ్సార్బర్లను (shock absorbers) ఎందుకు ఉపయోగిస్తారు?
జవాబు:
మోటారు సైకిళ్ళు, కార్లకు షాక్ అబ్సార్బర్లు లేదా ఆఘాత శోషకాలను అమర్చటం వలన ప్రచోదన బలము తగ్గి, గతుకుల రోడ్డులో ప్రయాణిస్తున్నప్పుడు, ప్రయాణికునికి ఎటువంటి హాని జరగకుండా ఉంటుంది.

మోటారుసైకిళ్ళు, కార్లకు షాకు అబ్సార్బర్లు లేదా ఆఘాత శోషకాలు ప్రచోదన కాలాన్ని పెంచుటకు వాడతారు. ఏదైని గుంతలోనికి వాహనం అకస్మాత్తుగా పడినపుడు, అది కుదుపును (జెర్క్) ఇస్తుంది. ఈ జెర్క్ ప్రచోదన బలాన్ని తగ్గించుటకు షాక్ అబ్సార్బర్లు లేదా అఘాత శోషకాలను వాడతారు. ప్రచోదనకాలం పెరుగుట వలన ప్రచోదన బలం తగ్గుతుంది.

ప్రశ్న 4.
సీమాంత ఘర్షణ, గతిక ఘర్షణ, దొర్లుడు ఘర్షణలను వివరించండి.
జవాబు:
సీమాంతర ఘర్షణ : నిశ్చలస్థితిలో ఉన్న వస్తువు బాహ్యబల ప్రయోగం వలన గమనంలోనికి రావడానికి ప్రయత్నిస్తున్న దాని గమనాన్ని నిరోధించే బలాన్ని స్థితిక ఘర్షణ (F) అని అంటారు. ఈ స్థితిక ఘర్షణ యొక్క గరిష్ఠ స్థాయిని సీమాంతర ఘర్షణ అంటారు.
∴ F_{s గరిష్ఠ} = F_s F ≤ μ_s N

“గతిక ఘర్షణ :
ఒక తలంపై జారుతున్న వస్తువు గమనాన్ని నిరోధించే బలాన్ని గతిక ఘర్షణ (F_k) అంటారు. దీనినే శుద్ధగతిక ఘర్షణ (లేదా) జారుడు ఘర్షణ అని అంటారు.

దొర్లుడు ఘర్షణ :
ఒక తలంపై దొర్లుతున్న వస్తువు గమనాన్ని నిరోధించే బలాన్ని దొర్లుడు ఘర్షణ అంటారు.

ప్రశ్న 5.
ఘర్షణ వల్ల కలిగే లాభాలు, నష్టాలను వివరించండి.
జవాబు:
ఉపయోగాలు :

1. భూమికి మరియు కాళ్లకు మధ్యగల ఘర్షణ వల్ల మనం సురక్షితంగా నడవగలుగుతున్నాం.
2. గోడలలోకి లేదా చెక్కలోకి మేకులను, మరలను చొప్పించినపుడు వాటిని పట్టి ఉండానికి ఘర్షణ బలం తోడ్పడును.
3. తాగే నీటిపాత్రను లేదా కలాన్ని పట్టుకోవడానికి ఘర్షణబలం చేతివేళ్ళకు తోడ్పడుతుంది.
4. వాహనాలు రోడ్లపై జారిపడిపోకుండా, అవి మలుపులు తిరగడానికి ఘర్షణ అవసరం.
5. యంత్రానికి అమర్చిన బెల్టు ద్వారా యాంత్రిక శక్తి ప్రసరణ ఘర్షణ బలం వల్లే సాధ్యమవుతుంది.

నష్టాలు :

1. ఘర్షణ వల్ల ఇంజన్లలో శక్తి నష్టం జరిగి, వాటి దక్షత కూడా తగ్గుతుంది.
2. ఘర్షణ వల్ల యంత్రభాగాలు అరిగిపోవడం వల్ల వాటి జీవితకాలం తగ్గుతుంది.
3. ఘర్షణ వల్ల యంత్రభాగాలు వేడెక్కుతాయి. దీనివల్ల వాటి పనిచేసే సామర్థ్యం తగ్గిపోతుంది.

ప్రశ్న 6.
ఘర్షణను తగ్గించే పద్ధతులను పేర్కొనండి. [Mar. ’14]
జవాబు:
ఘర్షణను తగ్గించే పద్ధతులు:
1) పాలిష్ చేయడం :
తలాలను పాలిష్ లేదా నునుపు చేయడం వల్ల తలాల మధ్య ఘర్షణను తగ్గించవచ్చును.

2) స్నేహకాలను (Lubricants) వాడటం :
స్పర్శలో ఉన్న రెండు తలాల మధ్య సన్నని ప్రవాహి లేదా నూనె పొరను ఉపయోగించడం వలన ఘర్షణను తగ్గించవచ్చును. ప్రత్యేకంగా తయారుచేసిన కర్బన (Organic) నూనెలు, సంపీడనం చెందింపబడిన గాలి మోదలైనవి సాధారణంగా ఉపయోగించే స్నేహకాలకు ఉదాహరణలు.

3) బాల్ బేరింగ్లు ఉపయోగించడం:
సైకిళ్ళు, ద్విచక్ర వాహనాలు, మోటారు కార్లు, డైనమోలాంటి స్వేచ్చగా తిరిగే వాహన చక్రాల మధ్య భాగాలకు బాల్ బేరింగ్లను అమర్చుట వలన జారుడు ఘర్షణను, దొర్లుడు ఘర్షణగా మార్చి ఘర్షణను తగ్గించవచ్చును.

4) ధారావాహికా కారం (Streamling) :
మోటారు వాహనాలు, విమానాలు మొదలైన వాటిని వాటి తలాలు వక్రంగా ఉండేటట్లు ప్రత్యేకమైన ఆకారంలో రూపొందిస్తారు. దానివల్ల అవి గమనంలో ఉన్నప్పుడు గాలి పొరలు, ధారారేఖలుగా రూపాంతరం చెందడం వల్ల ఘర్షణ తగ్గుతుంది.

ప్రశ్న 7.
దొర్లుడు ఘర్షణ నియమాలను తెలపండి.
జవాబు:

1. దొర్లుడు ఘర్షణ అనేది గతిక ఘర్షణ యొక్క ప్రత్యేక సందర్భము.
2. స్పర్శావైశాల్యం తక్కువగా ఉన్న దొర్లుడు ఘర్షణ తక్కువగా ఉండును.
3. దొర్లుతున్న వస్తువు వ్యాసార్థం ఎక్కువగా ఉన్న ఈ ఘర్షణ తక్కువగా ఉండును.

ప్రశ్న 8.
లాన్ రోలర్ (lawn roller) ను నెట్టడం కంటే లాగడం తేలిక. ఎందుకు?
జవాబు:
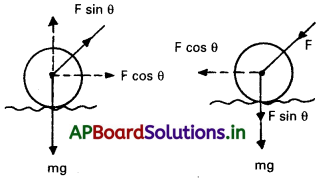
i) లాన్ రోలర్ను ఏటవాలు బలంతో లాగడం :
ఒక లాన్ రోలర్ను క్షితిజ సమాంతరంలో θ కోణం చేస్తున్న ‘F’ బలమునుపయోగించి పటంలో చూపినట్లు లాగినాము అనుకొనుము. వస్తువు యొక్క భారము, “mg” నిట్టనిలువుగా కింది వైపుకు పనిచేయును.

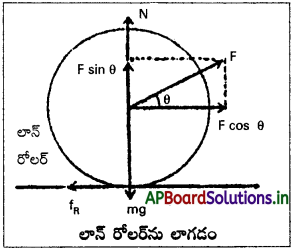
బలం ‘F’ యొక్క రెండు లంబాంశాలలో ఒక అంశం F sin θ నిట్టనిలువుగా పైకి, మరొక అంశం F cos θ రోలర్ను లాగటానికి, ఉపయోగపడును. పటము నుండి N + F sin θ
∴ అభిలంబ ప్రతిచర్య N mg – F sin θ
రోలర్పై పనిచేస్తున్న ఘర్షణ బలం F_R = µ_RN.
ఇక్కడ µ_R = దొర్లుడు ఘర్షణ గుణకం
F_R = µ_R (mg – F sin θ)
∴ లాగటానికి ఉపయోగపడు ఫలిత బలం
P = F cos θ – f_R = F cos θ – μ_R (mg – F sin θ)
∴ P = F(cos θ + μ_R sin θ) – μ_R mg ……….. (1)

ii) లాన్ రోలర్ను ఏటవాలు బలంతో నెట్టడం :

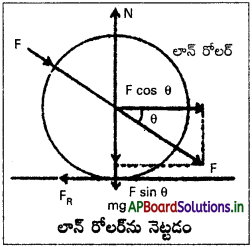
లాన్ రోలర్ను క్షితిజ సమాంతరంతో ‘θ’ కోణం చేస్తున్న బలం ‘F’ ని ఉపయోగించి పటములో చూపిన విధంగా నెట్టినామనుకోనుము.

అప్పుడు ఈ బలం యొక్క క్షితిజ లంబాంశము F sin θ నిట్టనిలువుగా క్రిందికి మరియు సమాంతర అంశం F cos θ రోలర్ను పటంలో చూపబడినట్లుగా కుడివైపుకు నెట్టుటకు ఉపయోగపడును.

లాన్ రోలర్ యొక్క భారం ‘mg’ నిట్టనిలువుగా కిందికి పనిచేయును.
∴ అభిలంబ ప్రతిచర్య N = mg + F sin θ
లాన్ రోలర్పై పనిచేయు ఘర్షణ బలం
F_R = μ_RN = μ_R (mg + F sin θ)
∴ నెట్టుటకు ఉపయోగపడు ఫలిత బలం
P’ = F cos θ – f_R = F cos θ – μ_R (mg + F sin θ)
P’ = F(cos θ – μ_R sin θ) – μ_R mg …………. (2)

సమీకరణాలు (1) మరియు (2)ల నుండి లాన్ రోలర్ను నెట్టుట కంటే లాగుట సులభం అని తెలియును.

దీర్ఘ సమాధాన ప్రశ్నల

ప్రశ్న 1.
a) న్యూటన్ రెండవ గమన నియమాన్ని తెలపండి. దాని నుంచి గమన సమీకరణం F = ma ను రాబట్టండి. [May; Mar. ’13]
b) ఒక వస్తువు వృత్త పథంలో ఎప్పుడూ సమవడితో చలిస్తూ ఉంటే దాని మీద బలం పనిచేస్తుందా?
జవాబు:
a) న్యూటన్ రెండవ గమన సూత్రం :
“ఒక వస్తువు యొక్క ద్రవ్యవేగంలోని మార్పురేటు ఆ వస్తువుపై ప్రయోగించిన బాహ్య బలానికి అనులోమానుపాతంలో ఉండి, బాహ్యబలం పనిచేసే దిశలో ఉంటుంది”.
ఇక్కడ బాహ్యబలం అంటే బాహ్యంగా వస్తువు మీద పనిచేసే ఫలిత బలం అని అర్ధము.
F = ma ఉత్పాదన :
ఒక వస్తువు ద్రవ్యరాశి ‘m’, వేగము ” ల లబ్దమును వస్తువు ద్రవ్యవేగం ‘P’ అంటారు.
∴ P = mv ………. (1)
న్యూటన్ రెండవ గమన సూత్రం నుంచి
ద్రవ్యవేగంలోని మార్పురేటు α వస్తువుపై పనిచేసే ఫలిత బలము.
\(\frac{dp}{dt}\) α F, (లేదా) F dp = K.\(\frac{dp}{dt}\) ………….. (2)
P విలువను పై సమీకరణంలో వ్రాయగా
F = K\(\frac{d(mv)}{dt}\) = Km\(\frac{dv}{dt}\) = Kma …………. (3)
∴ F = Kma
వేగంలోని మార్పురేటు \(\frac{dv}{dt}\), వస్తువు త్వరణం అగును.

ప్రమాణం :
S.I లో న్యూటన్:
ఒక కిలోగ్రాము ద్రవ్యరాశి గల వస్తువు మీద పనిచేసినపుడు ఆ వస్తువులో 1 ms^-2 త్వరణాన్ని కలుగచేసే బలాన్ని ఒక న్యూటన్ అంటారు.

అంటే సమీకరణం (3) లో m = 1, a = 1 అయితే F = 1 అవుతుంది, దీని నుంచి K = 1 అవుతుంది.
కాబట్టి F = \(\frac{dp}{dt}\) = ma
∴ F = ma

ఒక వస్తువు వృత్త పథంలో సమవడితో ప్రయాణిస్తున్నదనుకొనుము. వృత్తంపై ఏదైనా బిందువు వద్ద గీచిన స్పర్శరేఖ, ఆ బిందువు వద్ద వేగాన్ని తెలియచేయును. కావున వేగం యొక్క దిశ నిరంతరము మారుచుండుట వలన ఆ వస్తువుకు త్వరణం ఉండును. అందువలన సమవడితో ప్రయాణిస్తున్న వస్తువుపై బలం పనిచేయును.

ప్రశ్న 2.
ఘర్షణ కోణం, విశ్రామ కోణాలను నిర్వచించండి. గరుకు వాలుతలం విషయంలో ఘర్షణ కోణం, విశ్రామ కోణానికి సమానమని చూపండి. గరుకు క్షితిజ సమాంతర తలంపై 4 kg ద్రవ్యరాశి ఉన్న ఒక చెక్క దిమ్మె విరామస్థితిలో కలదు. దిమ్మెపై 30 N క్షితిజ సమాంతర బలాన్ని ప్రయోగిస్తే అది కదలడానికి సిద్ధం అయ్యింది. g = 10 m/s² అయితే, దిమ్మెపై ఆ తలం ప్రయోగించే మొత్తం స్పర్శా బలాన్ని కనుక్కోండి.
జవాబు:
ఘర్షణ కోణం :
“అభిలంబ ప్రతిచర్య మరియు సమాంతర ఘర్షణల ఫలిత బలం, అభిలంబ ప్రతిచర్యతో చేసే కోణాన్ని, ఘర్షణ కోణం అని అంటారు. దీనిని ‘Φ’ తో సూచిస్తారు.

ప్రక్క పటంలో చూపబడినట్లు క్షితిజ సమాంతర గరుకు తలంపై దీర్ఘచతురస్రాకార దిమ్మె ఉన్నదనుకొనుము.
పటం నుండి OC = N మరియు F_L ల ఫలిత బలము.
Φ = అభిలంబ ప్రతిచర్యతో ఫలిత బలం చేసే కోణము.
N =OB = అభిలంబ ప్రతిచర్య.

∴ ఘర్షణ కోణము యొక్క tan విలువ ఘర్షణ గుణకమునకు సమానము.

విశ్రామ కోణము :
వాలు తలం క్షితిజ సమాంతరంతో చేస్తున్న ఏ నిర్దిష్ట కోణము వద్ద వస్తువు వాలు తలం వెంబడి క్రిందకు ‘జారడానికి సిద్ధంగా ఉండునో, ఆ కోణాన్ని విశ్రామ కోణము అంటారు.

ఒక వాలు తలంను భావిద్దాం. వాలు తలం క్షితిజ సమాంతరంతో చేయు కోణాన్ని క్రమంగా పెంచుతూపోతే, ఒక నిరిష్ట కోణం (θ) వద్ద వస్తువు తలం వెంబడి కిందికి జారుటకు సిద్దంగా ఉంటుంది. ఈ వాలు తలం యొక్క కోణం θ ని విశ్రామ కోణం అని అంటారు.

వస్తువుపై పనిచేయు బలాలు :
i) వస్తువు యొక్క భారం ‘mg’ నిట్టనిలువుగా కిందికి పనిచేయును.
ii) తలం వెంబడి ఊర్ధ్వ దిశలో పనిచేయు ఘర్షణ బలం (F), Mg sin θ కు సమానము.
∴ F = Mg sine θ ……….. (2)

iii) అభిలంబ ప్రతిచర్య N తలానికి లంబంగా ఉండి, mg cos θ కు సమానమగును.

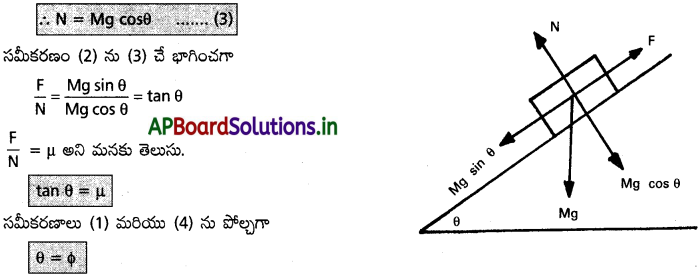
పై సమీకరణము నుంచి విశ్రామ కోణం, ఘర్షణ కోణాలు సమానము.

లెక్క :
సాధన:
ఇచ్చినవి m = 4kg; F = 30 N; g = 10 ms^-2

లెక్కలు (Problems)

ప్రశ్న 1.
ఒక కణం రేఖీయ ద్రవ్యవేగం, కాలం (t) ప్రమేయంగా p = a + bt గా ఇచ్చారు. a, b లు ధనాత్మక స్థిరాంకాలు అయితే, కణంపై పనిచేసే బలం ఏమిటి ?
సాధన:
కణం రేఖీయ ద్రవ్యవేగం p = a + bt
బలం F = \(\frac{dp}{dt}=\frac{d}{dt}\) (a + bt) = 0 + b
∴ F = b

ప్రశ్న 2.
10 kg ద్రవ్యరాశి ఉన్న వస్తువు వేగంలో 2 m/s మార్పు కలిగించడానికి 5 N బలాన్ని ఎంత కాలం ప్రయోగించాలి?
సాధన:
F = 5N, m = 10kg; (v – u) = 2m s^-1, t = ?
F = m\(\frac{(v-u)}{t}\)⇒\(\frac{10\times2}{t}\)
∴ t = 4s.

ప్రశ్న 3.
m ద్రవ్యరాశి ఉన్న ఒక బంతిని భూమిపై నుంచి నిట్టనిలువుగా పైకి విసిరితే అది క్షణ కాలం పాటు విరామస్థితికి వచ్చేలోపు h ఎత్తుకు చేరుకొంది. గురుత్వ త్వరణం g అనుకోండి. g బంతి తన ప్రయాణ కాలంలో గురుత్వాకర్షణ బలం వల్ల పొందే ప్రచోదనం ఎంత ? (గాలి నిరోధాన్ని విస్మరించండి)
సాధన:

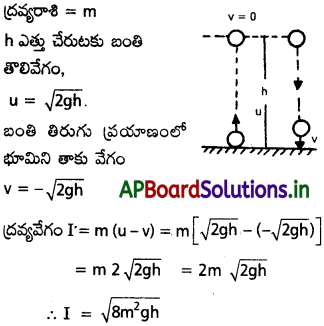
ప్రశ్న 4.
ఒక స్థిర బలాన్ని 3.0 kg ద్రవ్యరాశి ఉన్న వస్తువుపై 25 s కాలంపాటు ప్రయోగిస్తే, ఆ వస్తువు వేగం 2.0 ms^-1 నుంచి 3.5 ms^-1 కు మారింది. వస్తువు వేగ దిశలో మాత్రం ఎలాంటి మార్పులేదు. బలం పరిమాణాన్ని, బలం ప్రయోగించిన దిశను కనుక్కోండి.
సాధన:
m = 3.0 kg; u = 2.0 ms^-1,
v = 3.5ms^-1, t = 25 s;

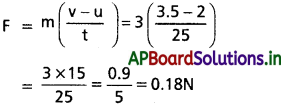
ఈ బలం దిశ వేగంలోని మార్పు దిశలో ఉండును.

ప్రశ్న 5.
ఒక లిఫ్ట్ గురుత్వ త్వరణంలో 1/3వ వంతు ఏకరీతి త్వరణంతో పైకి చలిస్తున్నప్పుడు లిఫ్ట్ ఉన్న వ్యక్తి దృశ్య భారం W. అదే లిఫ్ట్ గురుత్వ త్వరణంలో 1/2వ వంతు ఏకరీతి త్వరణంతో కిందికి చలిస్తున్నప్పుడు అతడి దృశ్యభారం ఎంత?
సాధన:
లిఫ్ట్ పైకి చలిస్తున్నప్పుడు, a = \(\frac{g}{3}\)
దృశ్యభారం W¹ m(g + a)

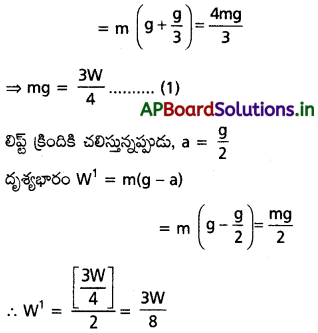
ప్రశ్న 6.
ఒక తెరచిన ట్రక్కు వెనక వైపు 200 kg ద్రవ్యరాశి ఉన్న ఒక పెద్ద పెట్టె విరామస్థితిలో కలదు. ట్రక్కు 1.5 m/s² త్వరణంతో ప్రయాణిస్తున్నప్పుడు ట్రక్కులోని పెట్టె జారిపోకుండా ఉండటానికి ట్రక్కు తలానికి, పెట్టెకు మధ్య ఉండవలసిన కనిష్ఠ స్థితిక ఘర్షణ గుణకం ఎంత?
సాధన:
m = 200kg, a = 1.5 ms^-2, g = 9.8 ms^-2
ma = μ_s  mg
μ_s = \(\frac{a}{g}=\frac{1.5}{9.8}\) = 0.153

ప్రశ్న 7.
భూమికి 40 m ఎత్తున తొలుత విరామస్థితిలో ఉన్న ఒక బాంబు అకస్మాత్తుగా పేలి, సర్వ సమానం అయిన రెండు ముక్కలుగా పేలింది. వాటిలో ఒకటి 10 m/s తొలి వేగంతో నిట్ట నిలువుగా కిందికి చలిస్తున్నది. బాంబు పేలిన 2 సెకన్ల తరవాత ఆ రెండు ముక్కల మధ్య దూరం ఎంత ? (గురుత్వ త్వరణం 10 m/s).
సాధన:
ఒక బాంబ్ విస్ఫోటనంలో 1 మరియు 2 భాగాలుగా విడిపోయినట్లు భావిద్దాం.
1వ భాగంనకు, u₁ = 10m/s, t = 2 sec;
g = 10m/s^-2, s₁ = ?
1వ భాగం స్థానభ్రంశం
s₁ = u₁t + \(\frac{1}{2}\)gt² =
= 10 × 2 × \(\frac{1}{2}\) × 10 × 2² = 40m

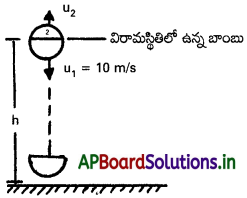
2వ భాగము, 1వ భాగం చలనంనకు వ్యతిరేక దిశలో శిఖరం నుండి ప్రక్షిప్తం చేసిన వస్తువు వలే చలించును. 2వ భాగంనకు u₁ = −u₁ = 10m/s

t = 2sec; g = 10 m/s²
2వ భాగం స్థానభ్రంశం,
s₂ = + u₂t + \(\frac{1}{2}\)gt²
= -10 × 2 × \(\frac{1}{2}\) × 10 × 2² = 0
∴ రెండు భాగాల మధ్యదూరం
= s₁ + s₂ = 40 + 0 = 40m

ప్రశ్న 8.
స్థిరంగా బిగించిన ఒక నునుపైన కప్పీ మీదుగా తేలికైన దారాన్ని అమర్చి, 2 దారం ఒక వైపు 4 kg ద్రవ్యరాశి, మరొక వైపు 3 kg ద్రవ్యరాశిని వేలాడదీశారు. ఈ 4 kg 3 kg ద్రవ్యరాశికి మరొక తేలిక దారంతో అదనంగా మరో 3 kg ద్రవ్యరాశి వేలాడదీశారు. విరామస్థితి నుంచి ఆ వ్యవస్థను లాగి వదిలితే, ఆ వ్యవస్థ ఉమ్మడి త్వరణం ఎంత ? (g = 10 m/s)

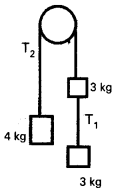
సాధన:
పటం నుండి,
m₁ = 3 + 3 = 6 kg.
m₂ = 4 kg
g = 10ms^-2
వ్యవస్థ త్వరణము

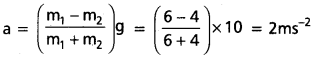
ప్రశ్న 9.
క్షితిజ సమాంతర తలంతో 30′ కోణం చేస్తున్న ఒక వాలుతలంపై 2 kg ద్రవ్యరాశి ఉన్న దిమ్మె జారుతుంది. దిమ్మెకు, వాలు తలానికి మధ్య ఘర్షణ గుణకం √3/2 ·
a) దిమ్మె ఎలాంటి త్వరణం లేకుండా కిందికి కదలాలంటే, దిమ్మెపై ఎంత బలాన్ని ప్రయోగించాలి?
b) దిమ్మె ఎలాంటి త్వరణం లేకుండా పైకి కదలాలంటే, దిమ్మెపై ఎంత బలాన్ని ప్రయోగించాలి?
సాధన:
m = 2kg; θ = 30°; µ = \(\frac{\sqrt{3}}{2}\)

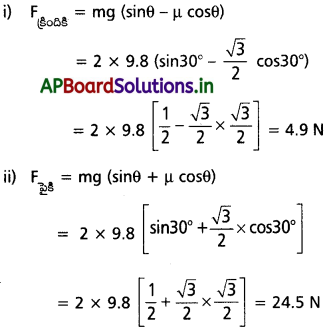
ప్రశ్న 10.
y = x²/20 అనే సమీకరణం సూచించే పరావలయ ఆకారంలో ఉన్న ఒక నునుపు తలంపై పటంలో చూపినట్లు ఒక దిమ్మెను ఉంచారు. µ_s = 0.5 అయితే, ఆ దిమ్మె జారిపోకుండా ఉండాలంటే, భూమి నుంచి ఎంత ఎత్తులో ఆ దిమ్మెను నునుపు తలంపై అమర్చాలి?
(tan θ = µ_s = \(\frac{dy}{dx}\))

సాధన:

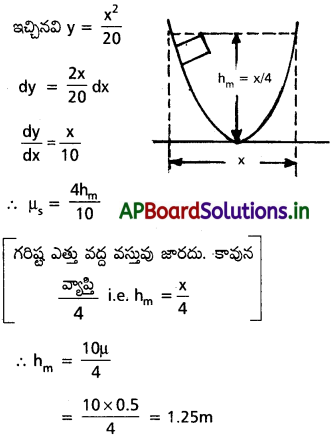
ప్రశ్న 11.
ఒక క్షితిజ సమాంతర టేబుల్పై 2 kg ద్రవ్యరాశి ఉన్న ఒక లోహపు దిమ్మెను ఘర్షణలేని కప్పీమీదుగా అమర్చిన దారం సహాయంతో 0.45 kg ల మరొక ద్రవ్యరాశికి కలిపారు. 0.45 kg ల ద్రవ్యరాశి కిందపడటం వల్ల లోహపు దిమ్మెపై క్షితిజ సమాంతర బలం పనిచేస్తుంది. టేబుల్, దిమ్మెకు మధ్య గతిక ఘర్షణ గుణకం 0.2 అయితే,

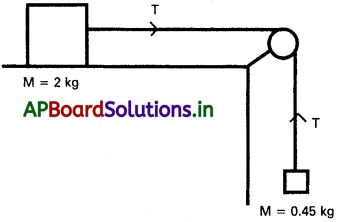
(a) తొలి త్వరణం, (b) దారంలో తన్యత, (c) దిమ్మె కదిలిన 2 సెకన్ల తరువాత దారం తెగిపోతే, దారం తెగిన తరవాత దిమ్మె కదిలే దూరం కనుక్కోండి.
సాధన:
ఇచ్చట m₁ = 0.45kg
m₂ = 2kg
m = 0.2
a) తొలి త్వరణం,

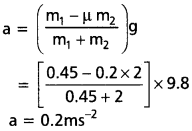
b) పటం నుండి,
T – f = m₂a
T – 3.92 = 2 × -0.2
కాని f = µm₂g
= 0.2 × 2 × 9.8 = 3.92 N
h_m = T – 3.92 = 2 × 0.2
⇒ T = 0.4 + 3.92 = 4.32 N

ప్రశ్న 12.
ఒక నునుపైన క్షితిజ సమాంతర తలం మీద 10 kg ద్రవ్యరాశి ఉన్న A అనే దిమ్మెను ఉంచారు. 5 kg ద్రవ్యరాశి ఉన్న B అనే మరొక దిమ్మెను పటంలో చూపినట్లు A దిమ్మెపై ఉంచారు. రెండు దిమ్మెల మధ్య ఘర్షణ గుణకం 0.4. క్రింది దిమ్మెపై 30 N క్షితిజ సమాంతర బలం ప్రయోగించారు. రెండు దిమ్మెల మధ్య ఉన్న ఘర్షణ బలం కనుక్కోండి. (g = 10 m/s² గా తీసుకోండి)

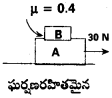
సాధన:
ఇచ్చట m_A = 10kg; m_B = 5kg;
F = 30N; µ = 0.4
F = (m_A + m_B)a
⇒ a = \(\frac{F}{(m_A+m_B)}\)
= \(\frac{30}{10+5}\)
= 2ms^-2
f = m_Ba = 5 × 2 = 10N

అదనపు లెక్కలు (Additional Problems)

(సౌలభ్యం కోసం g విలువ = 10 ms^-2 గా తీసుకోండి.)

ప్రశ్న 1.
కింది వాటిపై పనిచేసే నికర బలం పరిమాణం, దిశను తెలపండి.
a) స్థిర వడితో కిందికి పడుతున్న ఒక వర్షపు బిందువు.
b) నీటిలో తేలియాడుతున్న 10 g ద్రవ్యరాశి ఉన్న కార్క్,
c) ఆకాశంలో నైపుణ్యంతో విరామస్థితిలో ఉంచిన గాలిపటం.
d)ఒక గరుకు రోడ్డుపై 30 km/h వేగంతో ప్రయాణిస్తున్న కారు.
e) అన్ని ద్రవ్యాత్మక వస్తువులకు చాలా దూరంగా, విద్యుత్ అయస్కాంత క్షేత్రాల ప్రభావానికి లోనుకాకుండా అంతరాళంలో అత్యధిక వేగంతో చలిస్తున్న ఎలక్ట్రాన్.
సాధన:
a) వర్షం బిందువు స్థిరవడితో క్రిందికి పడిన, దాని త్వరణం a = 0. కావున నికర బలం F = ma = 0.

b) కార్క్ నీటిపై తేలుతున్నప్పుడు, దాని భారం, ఉత్పవన ‘బలంనకు సమానము. కావున కార్పై నికరబలం శూన్యం.

c) గాలిపటం నిశ్చలంగా వ్రేలాడుతున్న న్యూటన్ మొదటి నియమం ప్రకారం దానిపై నికర బలం శూన్యం.

d) ఘర్షణ బలంను అతిక్రమించుటకు బలంను ప్రయోగించాలి. కాని కారువేగం స్థిరమైన, దాని త్వరణం a = 0. కావున కారుపై పనిచేయు నికర బలం F = ma = 0.

e) ఎలక్ట్రాన్పై (గురుత్వవిద్యుత్ / అయస్కాంత) ఎటువంటి క్షేత్రం లేనప్పుడు, దానిపై నికరబలం శూన్యం.

ప్రశ్న 2.
0.05 kg ద్రవ్యరాశి ఉన్న ఒక గులకరాయిని నిట్టనిలువుగా పైకి విసిరారు. ఆ గులకరాయిపై పనిచేసే నికర బలం పరిమాణాన్ని, దిశను కింది సందర్భాలలో తెలియచేయండి.
a) నిలువుగా పైకి ప్రయాణిస్తున్నప్పుడు.
b) కిందికి ప్రయాణిస్తున్నప్పుడు.
c) గరిష్ఠ ఎత్తువద్ద క్షణకాలం పాటు విరామ స్థితిలో ఉన్నప్పుడు. ఒకవేళ గులకరాయిని క్షితిజ సమాంతర దిశతో 45° కోణంలో విసిరితే, మీ సమాధానాలు మారతాయా ? (గాలి నిరోధాన్ని విస్మరించండి)
సాధన:
ఒక వస్తువును నిలువుగా పైకి లేక క్రింది దిశలో చలిస్తే, భూమి గురుత్వాకర్షణ బలం వల్ల a = + g = + 9.8 ms^-2 త్వరణం క్రిందికి పనిచేయును. కావున పెబల్ (రాయి)పై నికరబలం అన్ని సందర్భాలలో నిలువుగా క్రిందికి పనిచేయును.
m = 0.05 kg మరియు a = + 9.8 ms^-2
∴ అన్ని సందర్భాలలో
F = ma = 0.05 × 9.8. 0.49 N,

పెబల్ (రాయిని) క్షితిజ సమాంతర దిశలో 45° కోణం చేయునట్లు విసిరిన, అది క్షితిజ మరియు లంబ అంశ వేగాలను కలిగి ఉండును. పెబల్పై ఈ అంశాలు ప్రభావంను చూపవు. కావున మన సమాధానము ఏ సందర్భంలో మారదు. ప్రతి సందర్భంలో (C), పెబల్ విరామస్థితికి రాదు. గరిష్ఠ ఎత్తు వద్ద పెబల్ క్షితిజ అంశమును కలిగి ఉండును.

ప్రశ్న 3.
0.1 kg ద్రవ్యరాశి ఉన్న ఒక రాయిపై పనిచేసే నికర బలం పరిమాణం, దిశను కింది సందర్భాలలో తెలపండి.
a) విరామస్థితిలో ఉన్న రైలు కిటికీ నుంచి బయటికి విసిరిన వెంటనే
b) 36 km/h స్థిర వేగంతో ప్రయాణిస్తున్న రైలు కిటికీ నుంచి బయటకు విసిరిన వెంటనే
c) 1 ms^-2 త్వరణంతో ప్రయాణిస్తున్న రైలు కిటికీ నుంచి బయటికి విసిరిన వెంటనే
d) 1 ms^-2 త్వరణంతో ప్రయాణిస్తున్న రైలు అడుగు తలంపై ఉన్నప్పుడు. రైలుతో సాపేక్షంగా రాయి విరామస్థితిలో ఉంది. పై అన్ని సందర్భాలలో గాలి నిరోధాన్ని విస్మరించండి.
సాధన:
a) ఇచ్చట m = 0.1 kg, a = +g = 9.8 m/s²
నికర బలం F = ma = 0.1 × 9.8 = ma = = 0.98 N
ఈ బలం నిలువుగా క్రింది దిశలో పనిచేయును.

b) రైలు స్థిరవేగంతో చలిస్తే, త్వరణం = 0. ఈ చలనం వల్ల రాయిపై బలం పని చేయదు.
∴ రాయిపై బలం F = రాయి భారం
= mg = 0.1 × 9.8 = 0.98 N
ఈ బలం నిలువుగా క్రింది దిశలో పనిచేయును.

c) రైలు 1m/s² త్వరణంతో చలిస్తే, అదనపు బలం F¹ = ma = = 0.1 × 1 = 0.1 N, రాయిపై క్షితిజ సమాంతరంగా పని చేయును. కాని రాయిని రైలు నుండి జారవిడిస్తే, F. శూన్యం మరియు రాయిపై = mg 0.1 × 9.8 = 0.98 N, నికరబలం F= నిలువుగా క్రిందికి పనిచేయును.

d) రైలు క్షితిజ సమాంతర దిశలో రాయి ఉంది. ఈ సందర్భంలో రాయిభారంను లంబ ప్రతిచర్య సంతులనం చేయును.

ప్రశ్న 4.
నునుపైన క్షితిజ సమాంతర బల్ల మీద l పొడవున్న దారం ఒక చివర m ద్రవ్యరాశి ఉన్న కణాన్ని, మరొక చివర చిన్న మేకుకు కలిపారు. కణం v వడితో వృత్తాకార మార్గంలో చలిస్తే, ఆ కణంపై పనిచేసే నికర బలం (వృత్తకేంద్రంవైపు పనిచేసే బలం).

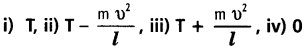
T దారంలోని తన్యత. సరైన సమాధానాన్ని ఎంచుకోండి.
సాధన:
కణంపై కేంద్రంవైపు నికరబలం T. ఇది, కణం వృత్తాకార మార్గంలో చలిస్తున్నప్పుడు అవసరమైన అభికేంద్రబలంను సమకూర్చుతుంది.

ప్రశ్న 5.
20 kg ద్రవ్యరాశి కలిగి, 15ms^-1 తొలి వేగంతో ప్రయాణిస్తున్న వస్తువుపై 50 N స్థిర అపత్వరణ బలాన్ని ప్రయోగిస్తే, ఎంత కాలం తరవాత అది ఆగిపోతుంది?
సాధన:
ఇచ్చట, F = -50 N, m = 20 kg
µ = 15 m/s, v = 0, t = ?

ప్రశ్న 6.
ఒక స్థిర బలాన్ని 3.0 kg ద్రవ్యరాశి ఉన్న వస్తువుపై 25 సెకన్లపాటు ప్రయోగిస్తే, ఆ వస్తువు వేగం 2.0 ms^-1 నుంచి 3.5 msc కు మారింది. వస్తువు వేగదిశలో మాత్రం ఎలాంటి మార్పులేదు. బలం పరిమాణాన్ని, బలం ప్రయోగించిన దిశను కనుక్కోండి.
సాధన:
ఇచ్చట m = 30 kg
µ = 2.0 m/s
v = 3.5 m/s,
t = 25s, F = ?
F = ma = \(\frac{m(v-u)}{t}=\frac{3.0(3.5-2.0)}{25}\)
= 0.18 N.
బలం చలన దిశలో పనిచేయును.

ప్రశ్న 7.
ఒకదానికి ఒకటి లంబంగా ఉన్న 8N, 6N పరిమాణం గల రెండు బలాలను 5 kg ద్రవ్యరాశి ఉన్న వస్తువుపై ప్రయోగించారు. వస్తువు త్వరణం పరిమాణాన్ని, దిశను తెలపండి.
సాధన:

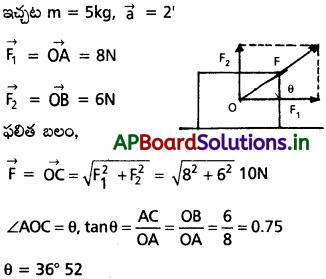
ఇదియే ఫలిత బలం దిశ మరియు వస్తు త్వరణ దశను ఇచ్చును.
a = \(\frac{F}{m}=\frac{10}{5}\) = 2ms^-2

ప్రశ్న 8.
ఒక ఆటో డ్రైవర్ రోడ్డు మధ్యలో ఉన్న బాలుని చూసి, ఆ బాలుణ్ని కాపాడటానికి 36 km/h వేగంతో పోతున్న తన ఆటోకు బ్రేకులు వేస్తే 4.0 s కాలంలో ఆగింది. ఆటోపై ప్రయోగించిన సరాసరి నిరోధ బలం ఎంత? ఆటో ద్రవ్యరాశి 400 kg, డ్రైవర్ ద్రవ్యరాశి 65 kg.
సాధన:
ఇచ్చట, u = 36km/h = 10 m/s, v = 0, t = s
m = 400 + 65 = 465 kg
అపబలం,

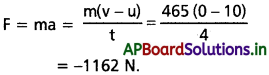
ప్రశ్న 9.
20,000 kg ద్రవ్యరాశి ఉన్న ఒక రాకెట్ను ఊర్థ్వ దిశలో పేల్చితే అది 5.0 ms^-2 తొలి త్వరణంతో ఆకాశంలోకి వెళ్ళిపోయింది. పేల్చినప్పుడు ప్రయోగించిన తొలి అభిబలం (thrust) కనుక్కోండి.
సాధన:
ఇచ్చట, m = : 20,000 kg = 2 × 10⁴ kg
తొలి త్వరణం = 5 m/s²
ఉత్థాపనం F = ?
ఊర్ధ్వత్వరణం 5 m/s² తో పాటు, ఉత్థాపనం, గురుత్వ బలంను వ్యతిరేకంగా పనిచేయును. బలం, నికర త్వరణంను ఏర్పరుచును.
9.8 + 5.0 = 14.8 m/s²
ఉత్థాపనం = బలం = ద్రవ్యరాశి × త్వరణం
∴ F = 2 × 10⁴ × 14.8

ప్రశ్న 10.
ప్రారంభంలో 10 ms^-1 స్థిర వేగంతో ఉత్తరం దిశలో ప్రయాణిస్తున్న 0.40 kg ద్రవ్యరాశి ఉన్న వస్తువుపై 8.0 N స్థిర బలాన్ని దక్షిణం దిశలో 30 సెకన్ల పాటు ప్రయోగించారు. బలం ప్రయోగించిన క్షణ కాలం వద్ద t = 0 అని, క్షణ కాలం వద్ద వస్తువు స్థానం x = 0 అని అనుకోండి. t = -5 s, 25 s, 100 s ల వద్ద వస్తువు స్థానాన్ని ఊహించండి.`
సాధన:
ఇక్కడ m = 0.40 kg, µ = 10m/s due N
F = -8.0 N
a = \(\frac{F}{m}=\frac{-80}{0.40}\) = -20 m/s²
for 0 ≤ t ≤ 30s
i) t = -5s వద్ద x = Ut = 10 × (−5) = -50m
ii) t = 25s వద్ద x = Ut + \(\frac{1}{2}\)at²
= 10 × 25 + \(\frac{1}{2}\) (-20) (25)² = – 6000m

iii) t = 100s వద్ద, లెక్క రెండు భాగాలుగా విడదీయ బడింది. 30s వరకు బలం / త్వరణం ఉండును.
∴ x₁ = Ut + \(\frac{1}{2}\)at²
= 10 × 30 + \(\frac{1}{2}\)(-20) (30)²
= -8700
t = 30s, v = U + at = 10 – 20 × 30
= – 590 m/s,
∴ 30s నుండి 100s చలనంలో,
x₂ = vt = -590 × 70 = – 41300 m
x = x₁ + x₂ = -8700 – 41300
= -50,000 m = – 50km.

ప్రశ్న 11.
ఒక ట్రక్ విరామస్థితి నుంచి బయలుదేరి 2.0 ms^-2 ఏకరీతి త్వరణంతో ప్రయాణిస్తుంది. t = 10 s తరవాత ట్రక్ పైకప్పుపై నిల్కొని ఉన్న వ్యక్తి ఒక రాయిని జారవిడిచాడు. (ట్రక్పైకప్పు భూమి నుంచి 6 m ల ఎత్తులో కలదు). 11 s వద్ద ఆ రాయి (a) వేగం, (b) త్వరణం కనుక్కోండి. (గాలి నిరోధాన్ని విస్మరించండి)
సాధన:
ఇక్కడ u = 0, a = 2 m/s², t = 10s

రాయి జారవిడిచినపుడు ట్రక్కు వేగం v
v = u + at నుండి
v = 0 + 2 × 10 = 20m/s

a) రాయిని వదిలినపుడు, క్షితిజ సమాంతర వేగం,
v_x = v = 20 m/s.
గాలి నిరోధంను విస్మరిస్తే, v_x స్థిరాంకము నిలువు దిశలో, రాయి తొలివేగం u = 0,
a = g = 9.8 m/s².
కాలం t = 11 – 10 = 1s
v = u + at నుండి
v_y = 0 + 9.8 × 1 = 9.8 ms^-1
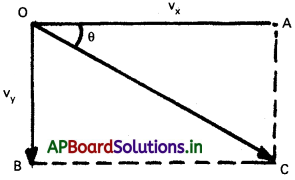
రాయి ఫలిత వేగంను OC ఇస్తుంది.
v = \(\sqrt{v_x^2+v_y^2}=\sqrt{20^2+9.8^2}\)
v = 22.3 m/s.
రాయి ఫలిత వేగం OC, క్షితిజ సమాంతర దిశ OA తో చేయు కోణం θ పటం నుండి
tan θ = \(\frac{v_y}{v_x}=\frac{9.8}{20}\) = 0.49
∴ θ = 29

b) కారు నుండి రాయిని వదిలినపుడు, క్షితిజ సమాంతర బలం = 0. త్వరణం ఒక్కదానిని కలిగి, పరావలయ పథంలో చలించును.

ప్రశ్న 12.
0.1 kg ద్రవ్యరాశి ఉన్న ఒక గోళాన్ని 2 m పొడవు ఉన్న దారంతో ఒక గదిలోని లోకప్పు (celing) కు వేలాడదీశారు. గోళం డోలనాలు చేయడం ప్రారంభిస్తే, మాధ్యమిక స్థానం వద్ద గోళం వడి 1 ms^-1. ఒకవేళ దారాన్ని తెంపితే గోళం ప్రయాణించే పథం (trajectory) కింద సందర్భాలలో ఎలా ఉంటుంది? (a) ఏదైనా ఒక గరిష్ఠ స్థానం వద్ద, (b) మాధ్యమిక స్థానం వద్ద.
సాధన:
a) అంత్యస్థానం వద్ద గోళం వేగం శూన్యం. అంత్య స్థానం వద్ద తీగ తెగితే, ‘ఆ’ పనిచేయును. కావున, గోళం నిలువుగా క్రిందికి పడిపోవును.

b) మాధ్యమిక స్థానం వద్ద, గోళం వేగం 1m/s, చాపం స్పర్శరేఖ వెంట ఉండును. తీగ మాధ్యమిక స్థానంలో తెగితే పరావలయం పథంలో చలించును.

ప్రశ్న 13.
ఒక వ్యక్తి ద్రవ్యరాశి 70 kg. ఇతడు లిఫ్ట్ అమర్చిన బరువులు తూచే యంత్రంపై నిల్చొని ఉన్నాడు. ఆ లిఫ్ట్
a) 10 ms^-1 ఏకరీతి వేగంతో పైకి,
b) 5 ms^-2 ఏకరీతి త్వరణంతో కిందికి
c) 5ms^-2 ఏకరీతి త్వరణంతో పైకి చలిస్తుంది. ప్రతీ సందర్భంలో యంత్రం చూపే రీడింగ్ ఎంత?
d) ఒక వేళ లిఫ్ట్ను నడిపే యంత్రం పనిచేయక, భూమ్యాకర్షణ బలం వల్ల స్వేచ్ఛగా కిందికి పడిపోయినట్లయితే యంత్రం చూపే రీడింగ్ ఎంత?
సాధన:
ఇచ్చట, m = 70 kg, g = 9.8 m/s²
ప్రతి సందర్భంలోను భారం కొలిచే యంత్రం, ప్రతి చర్య R i.e. దృశ్యభారంను ఇచ్చును.
a) లిఫ్ట్ ఏకరీతి వడితో, పైకి చలిస్తే, దాని త్వరణం సున్నా.
R = mg 70 × 9.8 = 686N

b) లిఫ్ట్ క్రిందికి a = 5m/s² తో క్రిందికి చలిస్తే
R = m(g – a) = 70 (9.8 – 5) = 336 N

c) లిఫ్ట్ a 5 m/s² తో పైకి చలిస్తే
R = m(g + a) = 70 (9.8 + 5) = 1036 N
లిఫ్ట్ స్వేచ్ఛగా క్రిందికి చలిస్తే, a = g
∴ R = m (g – a) = m (g – g) = సున్న

ప్రశ్న 14.
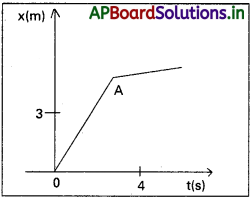
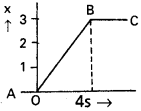
4 kg ద్రవ్యరాశి ఉన్న ఒక కణం స్థానం – కాలం వక్రం కింది పటంలో చూపడమైంది.
a) t < 0, t > 4 5, 0 < t < 4s కాలాల వద్ద కణంపై పనిచేసే బలం ఎంత?
b) t = 0, t = 4 s ల వద్ద ప్రచోదనం ఎంత? (ఏకమితీయ గమనం మాత్రమే తీసుకోండి)

సాధన:
i) t < 0, స్థాన-కాల గ్రాఫ్ 0A. దీని అర్థం కణం స్థానభ్రంశం సున్నా. i.e కణం విరామస్థితిలో మూల బిందువు వద్ద ఉండును. కావున కణంపై పనిచేయు బలం సున్నా.

ii) 0 < t < 4s, స్థాన-కాల గ్రాఫ్ OB స్థిరవాలును కలిగి ఉండును. కణం వేగం, ఈ అవధిలో స్థిరాంకం. i.e., కణం శూన్యత్వరణంను కలిగి ఉండును. కావున కణంపై బలం సున్నా.

iii) t > 4s, స్థాన-కాల గ్రాఫ్ BC కాలం అక్షంనకు సమాంతరం. మూలబిందువు నుండి 3m దూరంలో కణం విరామస్థితిలో ఉండును. కావున కణంపై బలం సున్నా.

iv) t = 0 వద్ద ప్రచోదనం
ప్రచోదనం = రేఖీయ ద్రవ్యవేగంలో మార్పు.
t = 0 ముందు కణం విరామస్థితిలో ఉండును.
i.e., u = 0. t = 0 తరువాత,
కణం స్థిరవేగం v = \(\frac{3}{4}\) = 0.75 m/s కలిగి ఉండును.

∴ ప్రచోదనం = m(v – u)
= u (0.75 – 0)
= 3 kg m/s
∴ t = 45 వద్ద ప్రచోదనం
t = 45 ముందు, కణం స్థిరవేగం u = 0.75 m/s
t = 4s తరువాత, కణం విరామస్థితిలో ఉండును.
i.e. v = 0
∴ ప్రచోదనం = m(v – u) = 4(0 – 0.75)
= -3kg ms^-1.

ప్రశ్న 15.
నునుపైన క్షితిజ సమాంతర తలంపై 10 kg, 20 kg ద్రవ్యరాశులు ఉన్న A, B అనే రెండు వస్తువులను వరసగా అమర్చి రెండింటిని తేలికైన దారంతో కలిపారు. F = 600 N క్షితిజ సమాంతర బలాన్ని దారం వెంబడి (i) A, (ii) Bల మీద ప్రయోగించారు. ప్రతీ సందర్భంలో దారంలో తన్యత ఎంత ?
సాధన:
ఇక్కడ, F = 500 N, m₁ = 10kg, m2 = 20kg
తీగలో తన్యత T మరియు బలప్రయోగ దిశలో వ్యవస్థ త్వరణం a.
a = \(\frac{F}{m_1+m_2}=\frac{500}{10+20}=\frac{50}{3}\)

a) పటం 3(a) నుండి భారదిమ్మెపై బలం ప్రయోగిస్తే
T = m₁ a = 10 × \(\frac{50}{3}\) N
T = 166.66 N

b) పటం 3(b) నుండి, తేలికైన దిమ్మెపై బలం,
T = m₂a = 20 × \(\frac{50}{3}\) N = 333.33 N

సందర్భం (a) లో, (b)లో T విలువలు వేర్వేరు కావున మన సమాధానం ద్రవ్యరాశిపై ప్రయోగించిన బలంపై ఆధారపడును.

ప్రశ్న 16.
8 kg, 12 kg ద్రవ్యరాశులను ఘర్షణ లేని కప్పీ మీదగా అమర్చిన తేలికైన, సాగని దారం సహాయంతో కలిపారు. ఆ వస్తువులను వదిలినప్పుడు ఆ వస్తువులు త్వరణాలను, దారంలోని తన్యతను కనుక్కోండి.
సాధన:
ఇక్కడ, m₂ = 8 kg, m₁ = 12kg

ప్రశ్న 17.
ప్రయోగశాల నిర్దేశ చట్రంలో ఒక కేంద్రకం విరామస్థితిలో కలదు. ఒకవేళ ఆ కేంద్రకం రెండు చిన్న కేంద్రకాలుగా విఘటనం చెందితే, ఆ రెండు కేంద్రకాలు వ్యతిరేక దిశలలో ప్రయాణిస్తాయని చూపండి.
సాధన:
ఉత్పన్నాల ద్రవ్యరాశులు m₁, m₂. వాని. వేగాలు v₁, v₂. విఘటనం తరువాత మొత్తం రేఖీయ ద్రవ్యరాశి = \(m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}\). విఘటనంనకు ముందు కేంద్రకం విరామ స్థితిలో ఉండును. విఘటనంకు ముందు దాని రేఖీయ ద్రవ్యవేగం సున్నా. రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమము ప్రకారం

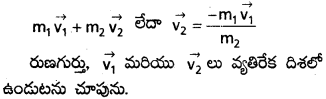
ప్రశ్న 18.
0.05 kg ద్రవ్యరాశి ఉన్న రెండు బిలియర్డ్స్ బంతులు 6 ms^-1 వేగంతో వ్యతిరేక దిశలలో ప్రయాణిస్తూ అభిఘాతం చెంది, ఆ తరవాత అంతే వేగంతో వెనకకు తిరిగి వచ్చాయి. ప్రతి బంతికి, రెండవ బంతి వల్ల అందే ప్రచోదనం కనుక్కోండి.
సాధన:
A బంతి తొలి ద్రవ్యవేగం = 0.05 (6) = 0.3 kg-m/s
అభిఘాతంలో వడి రివర్స్ అయిన, A బంతి తుది ద్రవ్యవేగం = 0.05 (-0.6) = – 0.3 kg-ms^-1
A బంతి ద్రవ్యవేగంలో మార్పు = -0.3 -0.3
= -0.6 kg m/s

ప్రశ్న 19.
100 kg ద్రవ్యరాశి ఉన్న తుపాకీని పేల్చినప్పుడు 0.020 kg ద్రవ్యరాశి ఉన్న బుల్లెట్ బయటికి వెలువడింది. తుపాకీ గొట్టం నుంచి బుల్లెట్ 80 ms^-1 వడి (muzzle speed) తో వెలువడితే, ఆ తుపాకి ప్రత్యావర్తన వడి ఎంత?
సాధన:
తూటా ద్రవ్యరాశి m = 0.02 kg
తుపాకి ద్రవ్యరాశి M = 100 kg
తూటా వడి V = 80 m/s
తుపాకి ప్రత్యావర్తన వడి V = ?

రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమము ప్రకారం
mv + MV = 0
V = \(\frac{-mv}{M}=\frac{-0.02\times80}{100}\) = 0.016 m/s

ప్రశ్న 20.
ఒక బ్యాట్స్మన్ 54 km/h తొలి వేగంతో ప్రయాణిస్తున్న బంతిని 45° కోణంలో తొలి వడిలో మార్పులేకుండా అపవర్తనం చెందించాడు. బంతికి అందిన ప్రచోదనం ఎంత? (బంతి ద్రవ్యరాశి 0.15 kg).
సాధన:

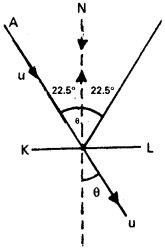
పటంలో బంతి AO వెంట బ్యాట్ను తాకి, OB వెంట పరావర్తనం చెందింది. ∠AOB = 45°. ON అభిలంబం.
∴ O = ∠NOA = 45°/2
= 22.5°

AO వెంట తొలివేగము = u = 54 km/h = 15 ms^-1
బంతి ద్రవ్యరాశి m = 0.15 kg

తొలివేగం uAO వెంట రెండు దీర్ఘ చతురస్ర అంశాలు కలిగి ఉండును. NO వెంట u cos θ మరియు OL వెంట u sin θ.
OB వెంట తుదివేగం పరిమాణం = u
uను ON వెంట u cos θ మరియు OL వెంట u sin θ అంశాలుగా విడదీయవచ్చు.

క్షితిజ సమాంతరంగా వేగం మారదు. కాని లంబ దిశలో వేగము రివర్స్ అగును.

బంతి రేఖీయ ద్రవ్యవేగంలో మార్పు
= m u cos θ – (- m u cos θ)
= 2 m u cos θ
= 2 × 0.15 × 15 cos 22.5°
= 4.5 × 0.9239 = 4.16 kg m/s

ప్రశ్న 21.
0.25 kg ద్రవ్యరాశి ఉన్న రాయిని దారం ఒక చివర కట్టి, 1.5 m ల వ్యాసార్ధం ఉన్న క్షితిజ సమాంతర వృత్తాకార పథంలో 40 rev./min వడితో తిప్పారు. దారంలో ఏర్పడే తన్యత ఎంత ? దారం భరించగల గరిష్ఠ తన్యత 200 N అయితే, రాయిని ఎంత గరిష్ఠ వడితో తిప్పగలం?
సాధన:
ఇక్కడ, m = 0.25 kg, r = 1.5 m
n = 40 rpm = \(\frac{40}{60}\), rps = \(\frac{2}{3}\), T = ?
T = mrw² = mr(2 πn)² = 4 π²rn²

ప్రశ్న 22.
ఒక వేళ, పై లెక్కలో (21) రాయి వేగాన్ని గరిష్ఠ వేగాన్ని అధిగమించేటట్లు పెంచితే, హఠాత్తుగా దారం తెగుతుంది. దారం తెగిన తరవాత, కింది వాటిలో ఏది రాయి ప్రయాణించే పథాన్ని తెలియచేస్తుంది?
a) రాయి వ్యాసార్ధం వెంబడి వెలుపలికి ప్రయాణిస్తుంది.
b) దారం తెగిన క్షణంలో, సర్శరేఖ దిశలో రాయి ఎగిరిపోతుంది.
c) స్పర్శా రేఖకు కొంత కోణంలో ఎగిరిపోతుంది. ఆ కోణం పరిమాణం రాయి వడిపై ఆధారపడి ఉంటుంది.
సాధన:
న్యూటన్ మొదటి నియమము ప్రకారము, తీగ తెగితే, రాయి స్పర్శరేఖ దిశలో చలించును.

ప్రశ్న 23.
ఎందుకో వివరించండి.
a) శూన్యాంతరాళంలో గుర్రం బండిని లాగలేదు, పరిగెత్తలేదు.
b) వేగంగా ప్రయాణిస్తున్న బస్సును హఠాత్తుగా ఆపితే, బస్సులో కూర్చున్న ప్రయాణీకులు, వాళ్ళు కూర్చున్న స్థలం నుంచి ముందుకు తూలుతారు.
c) లాన్ రోలర్ను నెట్టడం కంటే లాగడం తేలిక.
d) క్రికెటర్ బంతిని క్యాచ్ పట్టుకొనేటప్పుడు తన చేతులను వెనకకు లాగుతాడు.
సాధన:
a) గుర్రాలు, బండి లాగుటకు నేలను కొంతకోణంతో బలంను వెనుకకు నెట్టును. నేల కూడా గుర్రాలపై వ్యతిరేక దిశలో గుర్రాల కాళ్ళపై సమానమైన ప్రతి చర్య బలంను ప్రయోగించును. ఈ ప్రతిచర్య అంశ బలం బండిని చలింపచేయుటకు తోడ్పడును. ఖాళీ ప్రదేశంలో ప్రతిచర్యా బలం ఉండదు. కావున గుర్రం బండిని లాగలేదు.

b) దీనికి కారణం జఢత్వ చలనం వల్ల. స్పీడుగా వెళ్ళు బస్సు అకస్మాత్తుగా ఆగితే, సీటుతో స్పర్శలో ఉన్న ప్రయాణికుని శరీరం క్రింద భాగం నిశ్చల స్థితికి వచ్చును. పై భాగం చలన దిశలో ఉండును. కావున ప్రయాణికులు ముందుకు త్రోయబడుదురు.

c) లాన్ రోలర్న లాగునప్పుడు, ప్రయోగించు బలం యొక్క లంబ అంశం, రోలర్ ప్రభావ భారంను తగ్గించును. రోలర్ను నెట్టునప్పుడు ప్రయోగించు > బలం, లంబ అంశము రోలర్ ప్రభావ భారంను పెంచును. రోలర్ను నెట్టునప్పుడు కన్నా లాగునప్పుడు ప్రభావ భారం తగ్గును. కావున రోలర్ను లాగుట సులభం.

ప్రశ్న 24.
0.04 kg ద్రవ్యరాశి ఉన్న ఒక వస్తువు స్థానం – కాలం వక్రం పటంలో ఇవ్వడమైంది. ఈ గమనానికి తగిన భౌతిక సందర్భాన్ని సూచించండి. వస్తువు పొందిన రెండు వరస ప్రచోదనాల మధ్య కాలం ఎంత? ప్రతీ ప్రచోదనం పరిమాణం ఎంత?

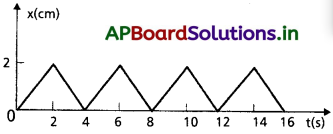
సాధన:
ఇచ్చట m = 0.04 kg
స్థాన-కాల గ్రాఫ్ కణం t = 0s వద్ద x = 0 నుండి 2 సెకనులలో x = 2 cm కు A వద్దకు చలించిందని భావిద్దాం.

x – t గ్రాఫ్ సరళరేఖ అయితే చలనం స్థిరవేగంను కలిగి ఉండును.
u = \(\frac{(2-0)cm}{(2-0)s}\) = 1 cm s^-1
= 10^-2 ms^-1

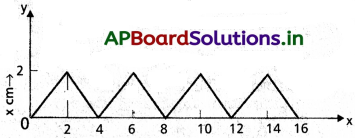
A వద్ద కణం x = 2 cm a, B వద్ద x = 0 కు 2 sec వెళుతుంది.

AB సరళరేఖ. చలనం స్థిరవేగంను కలిగి ఉండును. v = −1 cm/s = 10^-2 m/s

రుణ గుర్తు చలన వ్యతిరేక దిశను తెల్పును. ఇది పునరావృతం అవుతుంది. x = 0 మరియు x = 2 cmల వద్ద ఉన్న గోడల మధ్య పునరావృతం అయి గోడలను అభిఘాతం జరుపుతుంది. కావున బంతి ప్రతి 2 sec.లకు ప్రచోదనంను గ్రహిస్తుంది. ప్రచోదనం పరిమాణం మొత్తం రేఖీయ ద్రవ్యవేగంలో మార్పు.
= mu -(my)
= mu – mv = m(u – v)
= 0.04(10^-2 + 10^-2)
= 0.08 × 10^-2 = 8 × 10^-4 kg m/s

ప్రశ్న 25.
పటంలో చూపినట్లు, 1 ms^-2 త్వరణంతో తిరుగుతున్న క్షితిజ సమాంతర కన్వేయర్ బెల్ట్ప ఒక వ్యక్తి, బెల్టు సాపేక్షంగా విరామస్థితిలో నిల్చొని ఉన్నాడు. ఆ వ్యక్తిపై నికర బలం ఎంత? వ్యక్తి బూట్లకు, బెల్ట్కు మధ్య స్థితిక ఘర్షణ గుణకం 0.2 అయితే, బెల్ట్ త్వరణం ఏ విలువ వరకు బెల్ట్కు సాపేక్షంగా ఆ వ్యక్తి అదే విధంగా విరామస్థితిలో కొనసాగుతాడు? (వ్యక్తి ద్రవ్యరాశి = 65 kg.)

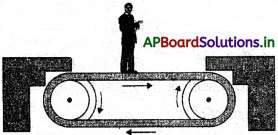
సాధన:
కన్వేయర్ బెల్టు త్వరణం, a = 1 m/s^-2
బెల్టు దృష్ట్యా నిశ్చలంగా నిల్చున్న వ్యక్తిత్వరణం = బెల్టు త్వరణం = a = 1 m/s²
m = 65 kg
వ్యక్తిపై నికర బలం F = ma = 65 × 1 = 65 N
µ = 0.2
లిమిటింగ్ ఘర్షణ బలం F = µR = umg
వ్యక్తి బెల్టు గరిష్ట త్వరణంతో చలించునపుడు,
F = ma¹ = µ mg
a¹ = mg = 0.2 × 9.8 1.96 ms^-1

ప్రశ్న 26.
దారం ఒక చివర కట్టిన m ద్రవ్యరాశి ఉన్న రాయి R వ్యాసార్థం ఉన్న నిలువు వృత్త పథంలో పరిభ్రమిస్తుంది. ఆ వృత్త నిమ్నతమ (Lowest), ఊర్థ్వతమ (Highest) బిందువుల వద్ద నిట్టనిలువుగా కిందికి పనిచేసే నికర బలాలు (సరియైన సమాధానం ఎన్నుకోండి).

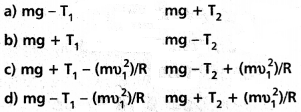
T₁, υ₁ లు నిమ్నతమ బిందువు వద్ద తన్యత, వడిని సూచిస్తాయి. T₂, υ₂ లు ఊర్థ్వతమ బిందువు వద్ద తన్యత, వడిని సూచిస్తాయి.
సాధన:
కనిష్ట బిందువు a వద్ద నికర బలం F_L = (mg – T₁) మరియు గరిష్ట బిందువు H వద్ద F_H = mg + T₂.
∴ (a) ఆప్షన్ కరెక్టు.

ప్రశ్న 27.
1000 kg ద్రవ్యరాశి ఉన్న ఒక హెలికాఫ్టర్ 15 ms^-2 నిలువు త్వరణంతో ‘ పైకిలేస్తుంది. హెలికాఫ్టర్ నడిపే వ్యక్తి, అందులోని ప్రయాణికుల భారం 300 kg కింది వివిధ సందర్భాలలో పనిచేసే బలం పరిమాణాన్ని, దిశను తెలియచేయండి.
a) హెలికాఫ్టర్ నడిపే వ్యక్తి, ప్రయాణీకుల వల్ల హెలికాఫ్టర్ అడుగు తలంపై పనిచేసే బలం
b) హెలికాప్టర్ రోటర్ (rotor) దాని పరిసరాలలోని గాలిపై జరిపే చర్య
c) పరిసరాలలో ఉన్న గాలి, హెలికాప్టర్పై . ప్రయోగించే బలం.
సాధన:
హెలికాఫ్టర్ ద్రవ్యరాశి, m₁ = 100kg
ప్రయాణికులు మరియు సిబ్బంది ద్రవ్యరాశి m₂ = 300 kg
ఊర్థ్వ త్వరణం a = 15 ms^-2
మరియు g = 10 ms^-2

a) హెలికాఫ్టర్ ఫ్లోర్పై ప్రయాణికులు మరియు సిబ్బంది వల్ల బలం = ప్రయాణికులు మరియు సిబ్బంది దృశ్యాభారం m₂(g + a)
= 300(10 + 15) = 7500 N

b) హెలికాఫ్టర్ రోటర్ చర్య పరిసర గాలిపై నిలువుగా క్రిందికి పనిచేయుట వల్ల, ప్రతి చర్య పైకి ఉండుట వల్ల హెలికాఫ్టర్ పైకి ఎగురుతుంది.
పనిచేయు బలం
F = (m₁ + m₂) (g + a)
= (1000+300) (10 + 15)
= 1300 × 25 = 32500 N

c) గాలి హెలికాఫ్టర్పై ప్రయోగించు బలమే ప్రతి చర్య. చర్య మరియు ప్రతిచర్యలు సమానము మరియు వ్యతిరేకం.
∴ ప్రతిచర్య బలం F¹ 32500 N, పై దిశలో

ప్రశ్న 28.
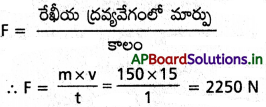
10^-2m² మధ్యచ్ఛేద వైశాల్యం ఉన్న ఒక పైపు ద్వారా నీటి ప్రవాహం 15 ms^-1 వేగంతో క్షితిజ సమాంతరంగా ప్రయాణిస్తూ బయటకు చిమ్మి, దగ్గరగా ఉన్న నిలువు గొడను తాకింది. గోడపై పతనం అయిన నీరు వెనకకు తిరిగి రాదని భావిస్తే నీటి వల్ల గోడపై కలిగే బలం ఎంత?
సాధన:
v = 15 ms^-1
మద్యచ్ఛేద వైశాల్యం a = 10² m^-2, F = ?
ఒక సెకనులో బయటకు నెట్టు నీటి ఘనపరిమాణం
= ax v = 10^-12 × m³ s^-1
నీటి సాంద్రత 10³ kg/m², గోడను / secలో తాకు
నీటి ద్రవ్యరాశి
m = (15 × 10^-2) × 10³ = 150 kg/s

ప్రశ్న 29.
రూపాయి నాణేలను పదింటిని ఒక దానిమీద ఒకటిగా ఒక బల్లపై ఉంచారు. ప్రతి నాణెం ద్రవ్యరాశి m కింది ప్రతి సందర్భంలో బల పరిమాణం, దిశను తెలపండి.
a) కింది నుంచి 7వ నాణెం మీద, పైనున్న నాణేల వల్ల బలపరిమాణం, దిశ
b) 8వ నాణెం వల్ల 7వ నాణెం మీద పనిచేసే బలపరిమాణం, దిశ
c) 6వ నాణెం వల్ల 7వ నాణెం మీద ప్రతిచర్య పరిమాణం, దిశ
సాధన:
a) 7వ కాయిన్పై, పైన ఉన్న మూడు కాయిన్స్ వల్ల బలం ఉండును.
∴ F = (3m) kgf = (3mg)N
ఇచ్చట g గురుత్వ త్వరణము.
ఈ బలం నిలువుగా క్రిందకు పని చేయును.

b) 8వ కాయిన్ బరువుతోపాటు పైన ఉన్న రెండు కాయిన్స్ బరువు కూడా 7వ కాయిన్పై పని చేయును. i.e., F = 2m + m = 3(m) kgf = (3mg)N బలం నిలువుగా క్రిందికి పనిచేయును.

c) 6వ కాయిన్ 4 కాయిన్స్ బరువు క్రింద ఉంది. ప్రతిచర్య, R = – F = −4m(kgf) = -(4 mg)N రుణగుర్తు, బరువుకు వ్యతిరేక దిశలో ప్రతిచర్య ఉండునని తెలుపును.

ప్రశ్న 30.
ఒక విమానం 720 km/h వడితో క్షితిజ సమాంతర వలయం ఆకారం (horizontal loop) లో ప్రయాణించింది. విమానం రెక్కల గట్టు కోణం 15°. ఆ వలయం వ్యాసార్ధం ఎంత?
సాధన:
θ = 15°
v = 720 km/h = \(\frac{720\times1000}{60\times60}\) = 200 ms^-1
g = 9.8 ms^-2
tan θ = \(\frac{v^2}{rg}\) నుండి
v² = rg tan θ

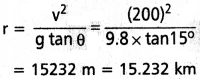
ప్రశ్న 31.
ఒక రైలు 54 km/h వడితో 30 m వ్యాసార్ధం ఉన్న గట్టు కట్టని (unbanked) వృత్తాకార రైలు మార్గం గుండా ప్రయాణిస్తుంది. రైలు ద్రవ్యరాశి 10⁶ kg. ఇంజన్, బోగీలు ఈ రెండింటిలో ఏది రైలుకు కావలసిన అభికేంద్ర బలాన్ని సమకూరుస్తుంది. పట్టాలు అరిగిపోకుండా ఉండాలంటే, ఎంత కోణంలో గట్టు కట్టాలి?
సాధన:
చక్రాలపై రెయిల్స్ ప్రయోగించి తిర్యక్ ఉత్థాపనమును అభికేంద్ర బలం ఇస్తుంది. న్యూటన్ 3వ గమన నియమము ప్రకారం, రైలు సమాన, వ్యతిరేక బలంను రెయిల్స్ (రైలు పట్టాలు) ప్రయోగించుట అరుగుదల ఉండును.

రైలు వెలుపలి రెయిల్పై హెచ్చు బలంను ప్రయోగించుట వల్ల త్వరగా అరిగిపోవును.

ప్రశ్న 32.
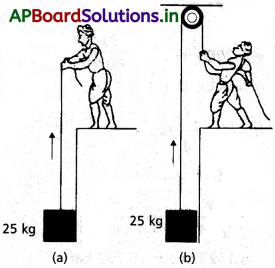
25 kg ద్రవ్యరాశి ఉన్న ఒక దిమ్మెను 50 kg ద్రవ్యరాశి ఉన్న వ్యక్తి పటంలో చూపినట్లు రెండు భిన్న విధాలుగా పైకి లాగుతున్నాడు. ఈ రెండు సందర్భాలలో ఆ వ్యక్తి వల్ల తలంపై జరిగే చర్యను కనుక్కోండి. 700 N ల అభిలంబ బలం వద్ద ఆ తలం కుంగిపోతే, ఆ తలం కుంగి పోకుండా ఉండాలంటే దిమ్మెను పైకి లాగడానికి ఏ పద్ధతిని ఎన్నుకొంటాడు?

సాధన:
దిమ్మె ద్రవ్యరాశి m = 25 kg
వ్యక్తి ద్రవ్యరాశి M = 50 kg
దిమ్మెను పైకి లేపుటకు ప్రయోగించు బలం
F = mg = 25 × 9.8 = 245 N

a) పటంలో చూపినట్లు వ్యక్తి దిమ్మెను పైకి తీసుకువస్తే ఊర్థ్వ దిశలో వ్యక్తి ప్రయోగించు బలం పనిచేయును.
ఇది వ్యక్తి దృశ్యభారంను పెంచును. కావున ఫ్లోర్పై బలం
W¹ = W + F = 490 + 245 = 735 N

b) పటంలో చూపినట్లు వ్యక్తి దిమ్మెను పైకి తీసుకువస్తే, వ్యక్తి బలంను క్రింది దిశలో ప్రయోగించును. ఇది వ్యక్తి దృశ్యభారంను తగ్గించును. కావున ఫ్లోర్పై చర్య
W¹ = W – F = 490 – 245 = 245 N

ఫ్లోర్ 700 N అభిలంబ బలంను ప్రయోగించుట వల్ల, దిమ్మెను లేపుటకు పద్ధతి (b)ను ఎన్నుకుంటాడు.

ప్రశ్న 33.
40 kg ద్రవ్యరాశి ఉన్న పటంలో చూపినట్లు ఒక తాడు మీద పైకి ఎక్కుతున్నది. ఆ తాడు భరించగల గరిష్ఠ తన్యత 600 N. కింది వివిధ సందర్భాలలో ఎప్పుడు తాడు తెగిపోగలదు? ఆ కోతి

a) 6 m s^-2 త్వరణంతో పైకి ఎక్కుతున్నప్పుడు
b) 4 ms^-2 త్వరణంతో కిందికి దిగుతున్నప్పుడు
c) 5 ms^-1 ఏకరీతి వేగంతో పైకి మన ఎక్కుతున్నప్పుడు
d) దాదాపు గురుత్వ త్వరణంతో, స్వేచ్ఛగా తాడు నుంచి కిందికి పడుతున్నప్పుడు. (తాడు ద్రవ్యరాశిని ఉపేక్షించండి.
సాధన:
కోతి ద్రవ్యరాశి m = 40 kg
రోప్ తెగకుండా ఉండు గరిష్ట తన్యత T = 600 N
ప్రతి సందర్భంలోను, రోప్ (త్రాడు) నిజ తన్యత, కోతి దృశ్యభారం (R) నకు సమానం.
R విలువ Tని దాటితే రోప్ తెగుతుంది.

a) కోతి పైకి ప్రాకితే,
a = 6 ms^-2
R = m(g + a)
= 40(10 + 6) = 640 N (T కన్నా ఎక్కువ) కావున రోప్ తెగుతుంది.

b) కోతి a = 4 ms^-2 త్వరణంతో క్రిందికి చలిస్తే,
R = m(g – a) = 40(10 – 4) = 240 N ఇది T కన్నా తక్కువ.
∴ రోప్ (త్రాడు) తెగదు.

c) కోతి ఏకరీతి వడి v = 5 msతో పైకి ప్రాకితే, దాని త్వరణం a = 0
∴ R = mg = 40 × 10 = 400 N
ఇది T కన్నా తక్కువ.
∴ రోప్ (త్రాడు) తెగదు.

d) రోప్ వెంట కోతి గురుత్వాకర్షణ వల్ల. స్వేచ్ఛగా క్రిందికి పడితే, a = g
∴ R = m(g – a) = m (g – g) = సున్న కావున రోప్ తెగదు.

ప్రశ్న 34.
A, B అనే రెండు వస్తువుల ద్రవ్యరాశులు వరసగా 5 kg, 10 kg. వీటిని ఒక బ ఒక దానికొకటి స్పర్శలో ఉండేటట్లు, ద్రుఢమైన గోడను తాకేటట్లు (పటం) విరామస్థితిలో అమర్చారు. ఆ రెండు వస్తువులకు, బల్లకు మధ్య ఘర్షణ గుణకం 0.15. 200 N క్షితిజ సమాంతర బలాన్ని A పై ప్రయోగించారు.
a) A, B ల స్పర్శాతలం ప్రతిచర్య కనుక్కోండి.
b) A, B ల మధ్య చర్య-ప్రతిచర్య బలాలను కనుక్కోండి. గోడను తీసేస్తే ఏమవుతుంది? ఆ వస్తువుల గమనంలో ఉంటే (b) సమాధానం మారుతుందా? µ_s/, µ_k లు మధ్యభేదాన్ని ఉపేక్షించండి.

సాధన:
A వస్తు ద్రవ్యరాశి m₁ = 5 kg
B వస్తు ద్రవ్యరాశి m₂ = 10 kg

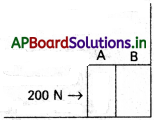
బల్ల మరియు రెండు వస్తువుల మధ్య ఘర్షణ గుణకం, µ = 0.15
వస్తువు Aపై ప్రయోగించిన క్షితిజ సమాంతర బలం F = 200 N

a) ఎడమవైపుకు పనిచేయు ఘర్షణ అవధి బలం
f = µ (m₁ + m₂)g
= 0.15(5+ 10) × 9.8 = 22.05 N
∴ పార్టిషన్పై కుడివైపు ప్రయోగించు నికర బలం
F’ = 200 – 22.05 = 177.95 N
పార్టిషన్ ప్రతిచర్య బలం = 177.95 N ఎడమవైపుకు

b) A వస్తువుపై ఘర్షణ అవధి బలం
f₁ = A వస్తువు B వస్తువుపై ప్రయోగించు నికర బలం
F¹¹ = F – F₁ = 192.65 N
ఇది కుడివైపు ఉండును.

A వస్తువుపై B వస్తువు ప్రతిచర్య = 192.65 N ఎడమవైపు పోర్షన్ను తొలగిస్తే, రెండు వస్తువుల వ్యవస్థ నికర బలంతో చలించును.
F’ = 177.95 N

వస్తువు Aలో చలనంను ఏర్పరచు బలం F, = m₁a
= 5 × 11.86 = 59.3 N

పోర్షన్ తీసివేసినపుడు A వస్తువు, B వస్తువుపై ప్రయోగించు నికర బలం
పోర్షన్ ను తొలగించినపుడు A పై వస్తువు B ప్రతిచర్య
= 133.35 N ఎడమవైపుకు
కావున (b) సమాధానాలు మారును.

ప్రశ్న 35.
పొడుగాటి ట్రాలీపై 15 kg ద్రవ్యరాశి ఉన్న దిమ్మెను ఉంచారు. ట్రాలీ అడుగు తలానికి, దిమ్మెకు మధ్య స్థితిక ఘర్షణ గుణకం 0.18. ఆ ట్రాలీ విరామస్థితి నుంచి బయలుదేరి 0.5 ms^-2 త్వరణంతో 20 సెకన్ల కాలంపాటు ప్రయాణించిన తరవాత ఏకరీతి వేగంతో ప్రయాణిస్తుంది. కింది రెండు సందర్భాలలో . దిమ్మె గమనాన్ని వివరించండి.
a) నేలపై విరామస్థితిలో ఉన్న పరిశీలకుని దృష్ట్యా
b) ట్రాలీతోపాటు ప్రయాణిస్తున్న పరీశీలకుని దృష్ట్యా.
సాధన:

a) m = 15 kg; µ = 0.18,
a = 0.5 ms ^-2
t = 20 s
ట్రాలీ చలించుట వల్ల దిమ్మెపై బలం F’ = ma
= 15 × 0.5 = 7.5 N
దిమ్మెపై ఘర్షణ అవధి బలం
= F = µR = µmg
= 0.18 × 15 × 9.8 = 26.46 N

ఇది దిమ్మె చలనంను వ్యతిరేకించును. దిమ్మె కదలదు, దిమ్మెలో స్టైతిక ఘర్షణ బలం F ప్రయోగించిన బలం F’కు సమానం మరియు వ్యతిరేకంగా ఉండును.

భూమిపై నిశ్చలంగా ఉన్న పరిశీలకుడు దిమ్మె ట్రాలీ దృష్ట్యా నిశ్చలంగా ఉన్నట్లు భావిస్తాడు. ట్రాలీ ఏకరీతి వేగంతో చలిస్తే, దిమ్మె అవిచ్ఛిన్నంగా నిశ్చలంగా ఉండును. ఈ సందర్భంలో ఊర్థ్వ బలం సున్నా. దిమ్మెపై ఘర్షణ బలం ఒక్కటే పనిచేయును.

b) ట్రాలీతో, పరిశీలకుడు త్వరణ చలనంతో చలిస్తే, పరిశీలకుడు అజఢత్వ చట్రంలో ఉండును. జఢత్వ నియమమును పాటించదు.

ప్రశ్న 36.
వెనక భాగం తెరచి ఉన్న ఒక ట్రాలీపై 40 kg ద్రవ్యరాశి ఉన్న ఒక పెట్టెను దాని తెరచిన కొన నుంచి 5 m ల దూరంలో పటంలో చూపినట్లు ఉంచారు. పెట్టెకు, ట్రాలీ అడుగు తలానికి మధ్య ఘర్షణ గుణకం 0.15. రుజు మార్గంలో ఉన్న రోడ్డు మీద, ట్రాలీ విరామస్థితి నుంచి బయలు దేరి 2 ms^-2 త్వరణంతో ప్రయాణిస్తుంది. ట్రాలీ బయలుదేరిన చోటు నుంచి ఎంత దూరం పోయిన తరవాత పెట్టె ట్రాలీ నుంచి కింద పడుతుంది? (పెట్టె పొడవును ఉపేక్షించండి)

సాధన:
బాక్స్ ద్రవ్యరాశి m = 40 kg
ట్రక్కు త్వరణం a = 2 ms^-2
తెరిచిన చివరి నుండి బాక్స్ దూరం, 5 = 5 m₁
ఘర్షణ గుణకం µ = 0.15
ట్రక్కు త్వరణ చలనం వల్ల బాక్స్పై బలం, F = ma
= 40 × 2 = 80 N
ఈ బలం ఊర్ధ్వ దిశలో ఉండును.
బాక్స్పై ప్రతిచర్య బలం F’, Fకు సమానం.
F = 80 N వెనుక దిశలో ఉండును.
దీనిని ఘర్షణ అవధి బలం వ్యతిరేకించును.
f = µR = µmg
= 0.15 × 40 × 9.8
= 58.8 N ఊర్థ్వ దిశలో
∴ వెనుక దిశలో బాక్స్పై నికర బలం
p = F’ – F = 80 – 58.8 = 21.2 v
బాక్స్లో వెనుకదిశలో ఏర్పడు త్వరణం
a = \(\frac{p}{m}=\frac{21.2}{40}\) = 0.53 ms^-2

బాక్స్ ట్రక్కు నుండి జారిపడి, S = 5m ప్రయాణించుటకు పట్టుకాలం t అయితే,
S = ut + \(\frac{1}{2}\) at²
5 = 0 × t + \(\frac{1}{2}\) × 0.53t²
t = \(\frac{\sqrt{5\times2}}{0.53}\) = 4.34S
ఈ కాలంలో ట్రక్కు X దూరం ప్రయాణించితే,
S = ut + \(\frac{1}{2}\)at²
x = 0 × 4.34 + \(\frac{1}{2}\) × 2(4.34)² = 18.84 m

ప్రశ్న 37.
15 cm ల వ్యాసార్థం ఉన్న ఒక వృత్తాకార బిళ్ల 33 \(\frac{1}{3}\) rev/min వడితో పరిభ్రమిస్తుంది. బిళ్ల కేంద్రం నుంచి రెండు నాణేలను, 4 cm, 14.cm ల దూరంలో బిళ్లపై ఉంచారు. బిళ్లకు, నాణేలకు మధ్య ఘర్షణ గుణకం 0.15. వాటిలో ఏ నాణెం బిళ్లతోపాటు పరిభ్రమిస్తుంది.
సాధన:
రికార్డుపై, కాయిన్ తిరుగుతున్నప్పుడు ఘర్షణ బలం అభికేంద్ర బలంను ఏర్పరుచును. ఈ అభికేంద్రబలం చాలకపోతే రికార్డ్ నుండి కాయిన్ జారును.
ప్రతి చర్యా బలం R = mg
ఘర్షణ బలం µR = µmg
కావాల్సిన అభికేంద్ర బలం = \(\frac{mv^2}{r}\) లేక 3 mω²

రెండు కాయిన్స్కు µw లు సమానం. కాని r విలువలు వేర్వేరు.
జారకుండా ఉండుటకు కాయిన్స్ షరతు
µ mg ≥ mω² లేదా µg > rω² ….. (1)
మొదటి కాయిన్కు,

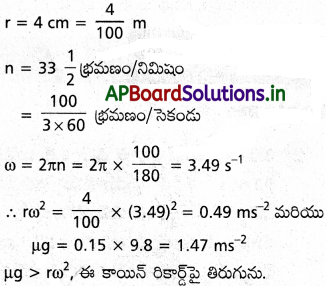
ప్రశ్న 38.
సర్కస్ గ్లోబులో మోటారు సైకిల్ను నిలువు వృత్తంలలో వివిధ రకాల భంగిమలలో అబ్బురపరిచే విన్యాసాలను అతి సులువుగా ప్రదర్శించడం మనం చూస్తూనే ఉంటాం. ( ఆ గ్లోబు గోళాకారంగా ఉండి, బయట నుంచి మనం చూడటానికి వీలుగా రంధ్రాలు కలిగి ఉంటుంది) గ్లోబులో మోటారు సైకిల్పై నిలువు వృత్తంలో పరిభ్రమించే ప్రదర్శకునికి (acrobat) కింది నుంచి ఎలాంటి ఆధారం లేకున్నా ఊర్ద్వతమ బిందువు వద్ద ఉన్నప్పుడు పడిపోకుండా ఉండటానికి కారణమేమిటో వివరించండి. నిలువు వృత్తంలో ఊర్ద్వతమ స్థానం వద్ద మోటారు సైకిల్పై గమనం పూర్తిచేయడానికి, నిమ్నతమ బిందువు వద్ద ఉండవలసిన కనిష్ఠ వేగం ఎంత? గ్లోబు వ్యాసార్థం 25 m.
సాధన:
డీక్వెల్ గరిష్ట బిందువు వద్ద, క్రింద నుండి ఆధారం లేకుండా మోటార్ సైక్లిస్ట్ క్రిందికి పడడు. దీనికి కారణం అతని భారం, అపకేంద్ర బలంనకు సమానం. మోటార్ సైక్లిస్ట్ భారం, అభికేంద్ర బలంను ఇచ్చును. కావున అతడు క్రిందికి పడడు. mv2 గరిష్ట బిందువు వద్ద, R + mg = = \(\frac{mv^2}{r}\)
ఇచ్చట R మోటార్ సైక్లిస్పై అభిలంబ ప్రతిచర్య క్రింది దిశలో ఉండును.
N = 0 అయిన వడి కనిష్టం.

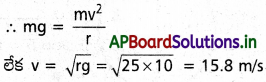
ప్రశ్న 39.
3m వ్యాసార్ధం ఉన్న ఒక బోలు స్థూపాకార డ్రమ్ దాని నిలువు అక్షంపరంగా, 200 rev/ min. వడితో పరిభ్రమిస్తుంది. 70 kg ద్రవ్యరాశి ఉన్న ఒక వ్యక్తి డ్రమ్ లోపలి గోడలకు తాకుతూ నిల్చొని ఉన్నాడు. వ్యక్తి బట్టలకు, డ్రమ్ గోడలకు మధ్య ఘర్షణ గుణకం 0.15. అడుగు తలాన్ని. హఠాత్తుగా తొలగించినప్పుడు, ఆ వ్యక్తి లోపలి గోడలకు అదే విధంగా తాకుతూ పడిపోకుండా ఉండాలంటే స్తూపాకార డ్రమ్కు ఉండాల్సిన కనిష్ఠ భ్రమణ వడి ఎంత?
సాధన:
m = 70 kg, r = 3 m
n = 200 rpm = \(\frac{200}{60}\) rps, µ = 0.15, 0 = ?
గోడ, వ్యక్తి ప్రయోగించు క్షితిజ సమాంతర బలం
N, అభికేంద్ర బలం = mrω²ను ఇచ్చును. ఈ సందర్భంలో వ్యక్తి భారంనకు వ్యతిరేకంగా ఊర్ధ్వ దిశలో ఘర్షణ బలం ఉండును.

ఫ్లోర్ను తీసివేస్తే, వ్యక్తి గోడకు అంటుకొని ఉండును.

ప్రశ్న 40.
R వ్యాసార్ధం ఉన్న ఒక వృత్తాకార వలయం దాని నిలువు వ్యాసాన్ని ఆధారంగా చేసుకొని, [ కోణీయ పౌనఃపున్యంతో పరిభ్రమిస్తుంది. వలయం మీద చిన్న పూసను ఉంచితే ω ≤ \(\sqrt{g/R}\) అయినప్పుడు అది వలయం నిమ్నతమ బిందువు వద్ద ఉంటుందని చూపండి. ω = \(\sqrt{2g/R}\) విలువకు వృత్త కేంద్రాన్ని, పూస మధ్య బిందువును కలిపే వ్యాసార్ధ సదిశ నిట్ట నిలువుగా కిందికి ఉండే దిశతో చేసే కోణం ఎంత? ఘర్షణ ఉపేక్షించండి.
సాధన:
పూస ఉన్న తీగ నిలువు వృత్తంలో తిరుగుతుంది. నిలువు. రేఖతో తీగ చేయు కోణం θ. అప్పుడు,

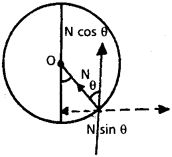
పటం నుండి mg = N cos θ ………… (1)
rω² = N sin θ ………… (2)
లేక m(R sin θ) ω² = N sin θ
లేక mRω² = N
(i) నుండి mg = mRω² 3 cos θ

సాధించిన సమస్యలు (Solved Problems)

ప్రశ్న 1.
అంతర్నక్షత్ర అంతరాళంలో ఒక వ్యోమగామి 100 m s^-2 స్థిర రేటు త్వరణంతో ప్రయాణిస్తూ తన చిన్న రోదసీ నౌక నుంచి అకస్మాత్తుగా వేరయినాడు. రోదసీ నౌక నుంచి బయటికి వచ్చిన తక్షణమే వ్యోమగామి త్వరణం ఎంత ? (వ్యోమగామిపై గురుత్వాకర్షణ బలాలను ప్రయోగించే ఇతర ఏ నక్షత్రాలు సమీపంలో లేవని భావించండి)
సాధన:
రోదసీ నౌక నుంచి బయటికి వచ్చిన వ్యోమగామిపై పనిచేసే నికర బలం శూన్యం. ఎందుకంటే వ్యోమగామి సమీపంలో అతనిపై గురుత్వాకర్షణ బలాలను ప్రయోగించే ఇతర ఏ నక్షత్రాలు లేవు. చిన్న రోదసీ నౌక వల్ల అతనిపై ప్రయోగించే గురుత్వాకర్షణ బలం కూడా ఉపేక్షించదగినంతగా ఉంటుంది. మొదటి నియమం ప్రకారం వ్యోమగామి త్వరణం శూన్యం.

ప్రశ్న 2.
0.04 kg ల ద్రవ్యరాశి ఉన్న ఒక బుల్లెట్ 90 m s^-1 వడితో ప్రయాణిస్తూ బరువైన చెక్క దిమ్మెలోకి ప్రవేశించి దిమ్మెలోపల 60 cm ల దూరం ప్రయాణించి ఆగిపోయింది. బుల్లెట్పై చెక్క దిమ్మె ప్రయోగించే సరాసరి నిరోధక బం ఎంత?
సాధన:
బుల్లెట్ రుణ త్వరణం a ను (స్థిరంగా భావించండి) కింది విధంగా ఇవ్వచ్చు.

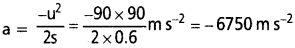
రెండవ నియమం ప్రకారం, నిరోధక బలం
= 0.04 kg × 6750 ms^-2 = 270 N

వాస్తవమైన నిరోధక బలం, బుల్లెట్ రుణ త్వరణం ఏకరీతిగా ఉండకపోవచ్చు. కాబట్టి, మన సమాధానం సరాసరి నిరోధక బలాన్ని మాత్రమే సూచిస్తుంది.

ప్రశ్న 3.
m ద్రవ్యరాశి ఉన్న కణం గమనాన్ని y = ut + \(\frac{1}{2}\)gt² అనే సమీకరణంతో వర్ణించడమైంది. ఆ కణంపై పనిచేసే బలం కనుక్కోండి.
సాధన:
y = ut + \(\frac{1}{2}\)gt²
కాని, v = \(\frac{dy}{dt}\)u + gt
త్వరణం, a = \(\frac{dv}{dt}\) = g
F = \(\frac{dp}{dt}\) = ma నుంచి బలం
F = ma = mg

ఈ విధంగా ఇచ్చిన సమీకరణం గురుత్వ త్వరణం వల్ల కలిగే కణం గమనాన్ని వివరిస్తుంది. ఆ దిశలో స్థాన నిరూపకం y.

ప్రశ్న 4.
ఒక బ్యాట్స్మెన్ 12 m s^-1 తొలి వడితో ప్రయాణిస్తున్న క్రికెట్ బంతిని దాని వడిలో మార్పు లేకుండా తిన్నగా బౌలర్ వైపుకు కొట్టాడు. బంతి ద్రవ్యరాశి 0.15 kg అయితే, బంతికి ఇచ్చిన ప్రచోదనం కనుక్కోండి. (బంతి చలనం రేఖీయ చలనం అనుకోండి)
సాధన:
ద్రవ్యవేగంలో మార్పు
= 0.15 × 12 – (-0.15 × 12) = 3.6 N s
ప్రచోదనం = 3.6 N s

బ్యాట్స్మెన్ నుంచి బౌలర్ దిశలో ఈ ప్రచోదనం ఉంటుంది.

బంతిపై బ్యాట్స్మెన్ ప్రయోగించే బలం; బంతి, బ్యాట్ కలిసి ఉండే కాలం తెలుసుకోవడం కష్టం అనడానికి ఇది మంచి ఉదాహరణ. కాని ప్రచోదనాన్ని మాత్రం చాలా తేలికగా లెక్కించగలిగాం.

ప్రశ్న 5.
రెండు సర్వసమాన బిలియర్డ్స్ బంతులు సమాన వడితో, వివిధ కోణాలతో పటంలో చూపించి నట్లు ఒక గోడను ఢీకొని, వాటి వడిలో ఎలాంటి మార్పు లేకుండా తిరిగి వెనకకు పరావర్తనం చెందాయి. కింది వాటిని కనుక్కోండి.
i) ప్రతీ బంతి గోడపై ప్రయోగించే బలదిశ,
ii) గోడ బంతులపై కలగచేసే ప్రచోదనాల నిష్పత్తి.

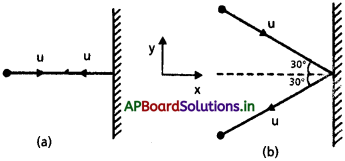
సాధన:
అంతర్బుద్ధితో (i) కి సమాధానం ఇవ్వచ్చు. గోడపై ప్రయోగించే బలం (a) సందర్భంలో గోడకు లంబంగా ఉంటుంది. అదే (b) సందర్భంలో గోడకు గీసిన లంబానికి 30° కోణంలో బలం ఉంటుంది. ఈ సమాధానం తప్పు. రెండు సందర్భాలలోను గోడపై బలం, గోడకు లంబంగా ఉంటుంది.

గోడపై పనిచేసే బలాన్ని ఎలా కనుక్కోవాలి? యుక్తితో రెండవ నియమాన్ని ఉపయోగించి గోడవల్ల బంతిపై కలిగే బలాన్ని (లేదా ప్రచోదనం) తెలుసుకొని, ఆ తరవాత మూడవ నియమంతో (i) కి సమాధానం ఇవ్వచ్చు. అభిఘాతానికి ముందు, తరవాత ప్రతీ బంతి వేగం U, ప్రతీ బంతి ద్రవ్యరాశి m అనుకోండి. పటంలో చూపినట్లు x, y అక్షాలను ఎన్నుకొని ప్రతి సందర్భంలో బంతి ద్రవ్యవేగంలో కలిగే మార్పును కనుక్కోవాలి.

సందర్భం (a) :
(p^x)_తొలి = mu (p^y)_తొలి = 0
(p_x) _తుది = – mu (P_y)_తుది = 0

ప్రచోదనం అంటే ద్రవ్యవేగ సదిశలో కలిగే మార్పు.
ప్రచోదనం X–అంశం = -2mu
ప్రచోదనం y-అంశం = 0

ప్రచోదనం, బలం రెండూ ఒకే దిశలో ఉంటాయి. ప్రచోదనం X–అంశాన్ని బట్టి గోడ బంతిపై ప్రయోగించే బలం గోడకు లంబంగా, రుణ X అక్షం దిశలో ఉంటుంది. ఇప్పుడు న్యూటన్ మూడవ గమన నియమాన్ని ఉపయోగిస్తే, బంతి గోడపై ప్రయోగించే బలం గోడకు లంబంగా, ధన X అక్షం వెంబడి ఉంటుంది. ఈ లెక్కలో బల పరిమాణం తెలుసుకోలేం. ఎందుకంటే, స్వల్ప అభిఘాత సమయాన్ని లెక్కలో ఇవ్వలేదు.
సందర్భం (b) :
(P_x)_తొలి =mu cos 30°
(P_y)_తొలి = – mu sin 30°
(P_x)_తుది = – mu cos 30°
(P_y)_తుది = -mu sin 30°

అభిఘాతం తరవాత p_x గుర్తు (దిశ) మారుతుంది. కాని p_y దిశ మారదు అని గమనించండి. కాబట్టి
ప్రచోదనం x-అంశం = -2 mu cos 30°
ప్రచోదనం y-అంశం = 0

ప్రచోచదనం (బలం) దిశ, సందర్భం (a)లోని బలదిశ లాగే గోడకు లంబంగా రుణ × అక్షం వెంబడి ఉంటుంది. పై విధంగానే న్యూటన్ మూడవ గమన నియమాన్ని ఉపయోగిస్తే, బంతి వల్ల గోడపై కలిగే బలం, గోడకు లంబంగా, ధన x అక్షం వెంబడి ఉంటుంది.

(a), (b) సందర్భాలలో గోడ బంతులపై కలగచేసే ప్రచోదనాల నిష్పత్తి,
2 mu / (2 mu cos 30°) = \(\frac{2}{\sqrt{3}}\) ≈ 1.2

ప్రశ్న 6.
పటంలో చూపినట్లు 6 kg ద్రవ్యరాశిని 2 m పొడవు గల తాడు సహాయంతో ఒక లోకప్పు (ceiling)కు వేలాడదీయడమైంది. ఆ తాడు మధ్య భాగం P వద్ద 50 N బలాన్ని క్షితిజ సమాంతర దిశలో ప్రయోగించారు. ఆ తాడు సమతాస్థితిలో ఉన్నప్పుడు నిట్టనిలువుతో చేసే కోణం ఎంత ? తాడు ద్రవ్యరాశిని విస్మరించండి. (g = 10 ms^-2 గా తీసుకోండి).

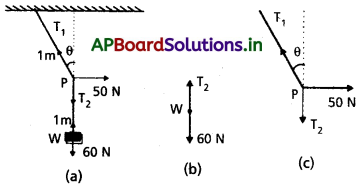
సాధన:
(b), (c) పటాలను స్వేచ్ఛా వస్తువు పటాలు అంటారు.
(b) W యొక్క స్వేచ్ఛా వస్తువు పటం, (c) P బిందువు యొక్క స్వేచ్ఛా వస్తువు పటం.
భారం W సమతాస్థితిని తీసుకొంటే,
T₂ = 6 × 10 = 60 N.
P బిందువు వద్ద పనిచేసే మూడు బలాలు, అవి వరసగా తన్యత T₁, తన్యత T₂, క్షితిజ సమాంతర బలం 50 N.

వీటి వల్ల P బిందువు సమతాస్థితిలో ఉంటుంది. ఫలిత బలం క్షితిజ సమాంతర అంశం, లంబ అంశలు రెండు వేరు వేరుగా సున్నా కావాలి.
T₁ cos θ = T₂ = 60N
T₂ sin θ = T₂ = 50N
tan θ = \(\frac{5}{6}\) లేదా θ = tan^-1(\(\frac{5}{6}\)) = 40°

తాడు నిట్టనిలువుతో చేసే కోణం, విస్మరించదగిన ద్రవ్యరాశి గల తాడు పొడవుపై గాని, క్షితిజ సమాంతర బలం ప్రయోగించిన బిందువుపైన గాని ఆధారపడటం లేదని గమనించండి.

ప్రశ్న 7.
ఒక పెట్టెను త్వరణంతో ప్రయాణిస్తున్న రైలులో ఉంచారు. రైలుతో సాపేక్షంగా పెట్టె విరామ స్థితిలో ఉండటానికి రైలుకు ఇవ్వగల గరిష్ఠ త్వరణాన్ని నిర్ధారించండి. పెట్టెకు, రైలు అడుగుభాగానికి మధ్య ఘర్షణ గుణకం 0.15.
సాధన:
స్థైతిక ఘర్షణ వల్ల పెట్టెకు త్వరణం కలుగుతుంది. కాబట్టి స్థైతిక ఘర్షణ నియమం ప్రకారం
ma = f_s ≤ µ_s N = µ_s mg
అంటే a ≤ µ_s g
∴ a_max = µ_sg = 0.15 × 10 m s^-2
= 1.5 m s^-2

ప్రశ్న 8.
4 kg ద్రవ్యరాశి ఉన్న ఒక దిమ్మె క్షితిజ సమాంతర తలంపై విరామస్థితిలో పటంలో చూపినట్లు ఉంది. ఆ తలం వాలును క్షితిజ సమాంతర తలంతో క్రమంగా θ = 15° వరకు పెంచినపుడు ఆ దిమ్మె జారడం ప్రారంభించింది. దిమ్మెకు, వాలు తలానికి మధ్య స్థితిక ఘర్షణ ఎంత?

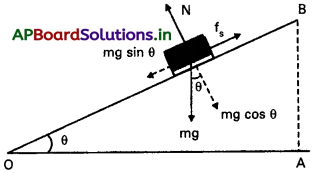
సాధన:
వాలు తలంపై విరామస్థితిలో ఉన్న m ద్రవ్యరాశి ఉన్న దిమ్మెపై పనిచేసే బలాలు (i) దిమ్మె భారం mg నిలువుగా అధో దిశలో (ii) వాలుతలం, దిమ్మె మీద ప్రయోగించే అభిలంబ ప్రతిచర్య బలం N (iii) జరగపోయే గమనాన్ని నిరోధించే స్థితిక ఘర్షణ బలం f_s. సమతా స్థితిలో ఈ మూడు బలాల ఫలిత బలం తప్పకుండా శూన్యం కావాలి. దిమ్మె భారం mg ని పటంలో చూపించి నట్లు రెండు దిశలలో విభేదనం (resolve) చేసినప్పుడు
mg sin θ = f₂, m g cos θ = N

వాలు కోణం θ పెరిగితే, స్వయం సర్దుబాటు ఘర్షణ బలం f₂ కూడా θ = θ_max అయ్యేదాక పెరుగుతుంది.
θ = θ_max వద్ద f₂ కూడా గరిష్ఠ విలువను పొందుతుంది.
(f₂)_max µ_s N

కాబట్టి, tan θ_max = µ_s లేదా θ_max = tan^-1 µ_s

θ విలువ θ_nm. కంటే కొద్దిగా ఎక్కువగా అయినప్పుడు దిమ్మెపై స్వల్ప నికర బలం పనిచేసి, దిమ్మె జారడం ప్రారంభిస్తుంది. θ_max విలువ ఘర్షణ గుణకం µ_s పై మాత్రమే ఆధారపడుతుంది కాని దిమ్మె ద్రవ్యరాశిపై ఆధారపడదు.
θ_max = 15° విలువకు µ_s = tan 15° = 0.27

ప్రశ్న 9.
ట్రాలీ, క్షితిజ సమాంతర తలానికి మధ్య గతిక ఘర్షణ గుణకం 0.04 అయితే, పటంలో చూపినట్లు ట్రాలీ, దిమ్మె వ్యవస్థ త్వరణం ఎంత ? దారంలో తన్యత ఎంత ? దారం ద్రవ్యరాశిని విస్మరించండి.
(g = 10 ms^-2 గా తీసుకోండి).

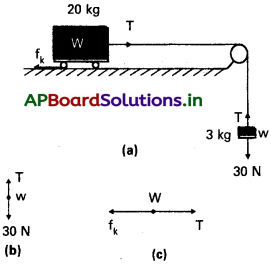
సాధన:
దారం సాగనిది, కప్పీ నునుపైనది కాబట్టి, 3 kg ద్రవ్యరాశి ఉన్న దిమ్మె, 20 kg ద్రవ్యరాశి ఉన్న ట్రాలీ రెండూ ఒకే పరిమాణంలో త్వరణాన్ని కలిగి ఉంటాయి. దిమ్మెకు రెండు గమన నియమాన్ని అనువర్తిస్తే పటం (b).
30 – T = 3a …………… (1)
ట్రాలీకి రెండవ గమన నియమాన్ని అనువర్తిస్తే,
(పటం (c)).
T – f_k = 20a
కాని, f_k = µ_k N, µ_k = 0.04
N = 20 × 10 = 200N

ట్రాలీ గమనాన్ని సూచించే సమీకరణం నుంచి,
T- 0.04 × 200 20 a లేదా
T – 8 = 20a ……… (1)
(1), (2) సమీకరణాల నుంచి,
a = \(\frac{22}{23}\) m s^-2 = 0.96 m s^-2, T = 27.1 N.

ప్రశ్న 10.
క్షితిజ సమాంతర రోడ్డుమీద 18 km/h వడితో. సైకిల్ తొక్కుతున్న వ్యక్తి తన వడిని తగ్గించు కోకుండా 3 m వ్యాసార్ధం ఉన్న వృత్తాకార మార్గంలో హఠాత్తుగా మలుపు తిరిగాడు. సైకిల్ టైర్లకు, రోడ్డుకు మధ్య స్థితిక ఘర్షణ గుణకం 0.1. సైకిల్ తొక్కే వ్యక్తి మలుపు తిరిగేటప్పుడు స్లిప్ అవుతాడా?
సాధన:
గట్టుకట్టని క్షితిజ సమాంతర రోడ్డుమీద సైకిల్ తొక్కే వ్యక్తి వృత్తాకార మార్గంలో జారిపోకుండా మలుపు తిరగాలంటే కావలసిన అభికేంద్ర బలాన్ని ఘర్షణ బలం ఒక్కటే సమకూర్చగలదు. కాని, వడి చాలా అధికంగా ఉన్నా లేదా మలుపు చాలా నైశిత్యంగా (sharp) ఉన్నా (చాలా తక్కువ వ్యాసార్ధ వృత్తాకార మార్గం) లేదా రెండూ కన్నా కావలసినంత అభికేంద్ర బలాన్ని సమకూర్చడానికి ఘర్షణ బలం సరిపోదు. అందువల్ల సైకిల్ తొక్కే వ్యక్తి స్లిప్ అవుతాడు. v_max = \(\sqrt{\mu_{\mathrm{s}} R_{\mathrm{g}}}\), స్లిప్ అవకుండా ఉండటానికి కావలసిన షరతును తెలియ చేస్తుంది.
v₂ ≤ μ_s Rg
పై లెక్కలో, R = 3m, g = 9.8 m s^-2, μ_s = 0.1
అయితే,

μ_sRg = 2.94 m²s^-2, v = 18 km/h = 5 ms^-1;
v² = 25 m² s అంటే పై నిబంధన పాటించలేదు. కాబట్టి సైకిల్ తొక్కే వ్యక్తి మలుపు తిరిగేటప్పుడు స్లిప్ అవుతాడు.

ప్రశ్న 11.
కార్ల పరుగు పందెం నిర్వహించడానికి 300 m వ్యాసార్ధంతో ఒక వృత్తాకార రేస్క్ (race track) ని నిర్మించారు. ఆ రేస్ ట్రాక్ 15° కోణంతో గట్టుకట్టబడింది. పరుగు పందెంలో పాల్గొనే కారు చక్రాలకు, రోడ్డుకు మధ్య ఘర్షణ గుణకం 0.2, (a) కారు టైర్ల అరుగుదల, తరుగుదలను నివారించడానికి కారుకు చాలా అనుకూలమైన వడి (optimum speed) ఎంత ఉండాలి? (b) కారు స్లిప్ అవకుండా ఉండటానికి, కారుకు అనుమతించ దగ్గ గరిష్ఠ వడి (permissible speed) ఎంత?
సాధన:
గట్టుకట్టిన రోడ్డు మీద కారు జారిపోకుండా వృత్తాకారంగా మలుపు తిరగాలంటే కావలసినంత అభికేంద్ర బలాన్ని అభిలంబ ప్రతిచర్య, ఘర్షణ బలాల క్షితిజ సమాంతర అంశాలు సమకూరుస్తాయి. అనుకూలమైన వడి వద్ద ఒక్క అభిలంబ ప్రతిచర్య అంశం కలిగించే సాధన. a) నేలపై చెక్క దిమ్మె విరామస్థితిలో కలదు. దాని స్వేచ్ఛా అభికేంద్ర బలం సరిపోతుంది. ఘర్షణ బలం అవసరం లేదు. v₀ = (R g tan θ)^1/2 అనుకూలమైన వడిని ఇస్తుంది.

ప్రశ్న 12.
2 kg ద్రవ్యరాశి ఉన్న ఒక చెక్క దిమ్మె మెత్తని క్షితిజ సమాంతర నేలపై విరామస్థితిలో కలదు. 25 kg ద్రవ్యరాశి ఉన్న ఒక లోహపు స్థూపాన్ని చెక్క దిమ్మెపై ఉంచినప్పుడు పటంలో చూపినట్లు నేల నిలకడగా కిందికి కుంగుతుంది. చెక్క. దిమ్మె, స్థూపం రెండూ కలిసి 0.1 ms త్వరణంతో కింది పోయాయి. క్షితిజ సమాంతర తలంపై చెక్క దిమ్మె జరిపే చర్య నేల (a) కుంగడానికి ముందు, (b) కుంగిన తరవాత ఎంత? లెక్కలో చర్య – ప్రతిచర్య జంటలను గుర్తించండి. g = 10 m s^-2 గా తీసుకోండి.

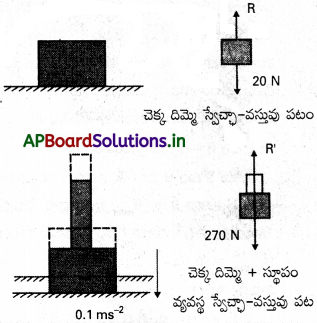
సాధన:
నేలపై చెక్క దిమ్మె విరామస్థితిలో కలదు. దాని స్వేచ్ఛా – వస్తువు పటం దిమ్మెపై ఉన్న రెండు బలాలను సూచిస్తుంది. ఒకటి భూమి వల్ల ఏర్పడే గురుత్వాకర్షణ 2 × 10 = 20 N; మరొకటి దిమ్మెపై తలం వల్ల ఏర్పడే అభిలంబ బలం R.R = 20N. మొదటి నియమం ప్రకారం దిమ్మెపై నికర బలం శూన్యం కావాలి. మూడవ నియమాన్ని ఉపయోగిస్తే, దిమ్మె తలంపై జరిపే చర్య (దిమ్మె తలంపై ప్రయోగించే బలం) 20 Nకు సమానం, ఇది నిలువుగా అధో దిశలో పనిచేస్తుంది.

(b) వ్యవస్థ (చెక్క దిమ్మె + స్థూపం). 0.1 ms^-2 త్వరణంతో కిందికి త్వరణం చెందుతుంది. వ్యవస్థ స్వేచ్ఛా వస్తువు పటం వ్యవస్థపై రెండు బలాలు పనిచేస్తున్నాయని సూచిస్తుంది. భూమి వల్ల ఏర్పడే భూమ్యాకర్షణ బలం (270 N); నేల వ్యవస్థపై ప్రయోగించే అభిలంబ బలం R’. స్వేచ్ఛా వస్తువు పటం దిమ్మె, స్థూపం మధ్య గల అంతర్గత బలాలను సూచించడం లేదు అని గమనించండి. వ్యవస్థకు రెండవ నియమాన్ని అనువర్తిస్తే,
270 – R’ = 27 × 0.1N
అంటే R’ = 267.3 N

మూడవ నియమం ప్రకారం, తలం కుంగిన తరవాత, వ్యవస్థ తలంపై జరిపే చర్య 267.3 N కు సమానం. ఇది నిలువుగా అధో దిశలో పనిచేస్తుంది.